2025年中考数学复习专练:第十二章 线段与角、相交线与平行线(含答案)
文档属性
| 名称 | 2025年中考数学复习专练:第十二章 线段与角、相交线与平行线(含答案) |
|
|
| 格式 | docx | ||
| 文件大小 | 97.4KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 通用版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2025-05-28 00:00:00 | ||
图片预览


文档简介
第十二章 线段与角、相交线与平行线
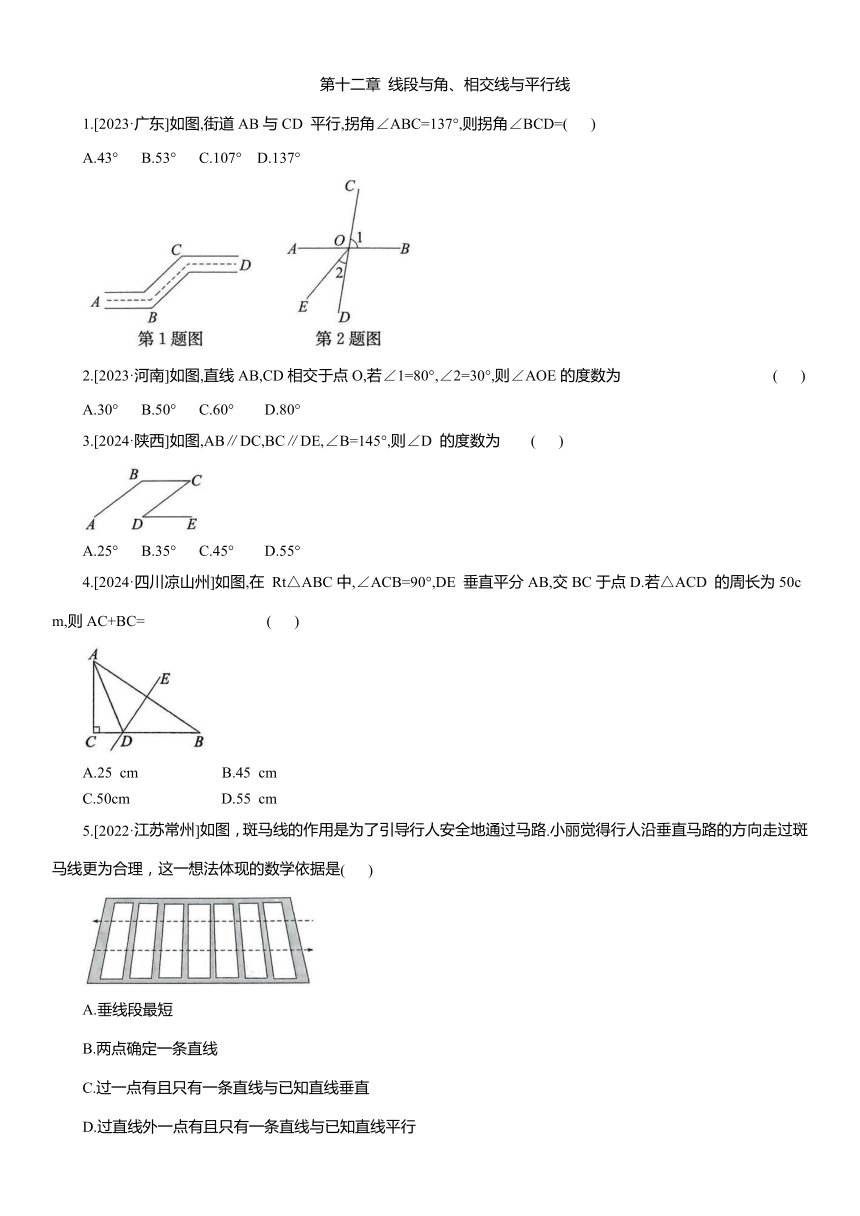
1.[2023·广东]如图,街道AB与CD 平行,拐角∠ABC=137°,则拐角∠BCD=( )
A.43° B.53° C.107° D.137°
2.[2023·河南]如图,直线AB,CD相交于点O,若∠1=80°,∠2=30°,则∠AOE的度数为 ( )
A.30° B.50° C.60° D.80°
3.[2024·陕西]如图,AB∥DC,BC∥DE,∠B=145°,则∠D 的度数为 ( )
A.25° B.35° C.45° D.55°
4.[2024·四川凉山州]如图,在 Rt△ABC中,∠ACB=90°,DE 垂直平分AB,交BC于点D.若△ACD 的周长为50cm,则AC+BC= ( )
A.25 cm B.45 cm
C.50cm D.55 cm
5.[2022·江苏常州]如图,斑马线的作用是为了引导行人安全地通过马路.小丽觉得行人沿垂直马路的方向走过斑马线更为合理,这一想法体现的数学依据是( )
A.垂线段最短
B.两点确定一条直线
C.过一点有且只有一条直线与已知直线垂直
D.过直线外一点有且只有一条直线与已知直线平行
6.[2023·四川达州]下列命题中,是真命题的是 ( )
A.平行四边形是轴对称图形
B.对角线互相垂直的四边形是菱形
C.到一条线段两个端点距离相等的点,在这条线段的垂直平分线上
D.在△ABC 中,若∠A: ∠B: ∠C=3:4:5,则△ABC是直角三角形
7.[2023·江苏苏州]如图,在正方形网格内,线段 PQ的两个端点都在格点上,网格内另有A,B,C,D四个格点.下列四个结论中,正确的是 ( )
A.连接AB,则AB∥PQ
B.连接BC,则BC∥PQ
C.连接BD,则BD⊥PQ
D.连接AD,则AD⊥PQ
8.[2023·山西]如图,一束平行于主光轴的光线经凸透镜折射后,其折射光线与一束经过光心O的光线相交于点 P,F为焦点.若∠1=155°,∠2=30°,则∠3的度数为 ( )
A.45° B.50° C.55° D.60°
9.[2023·四川南充]如图,在 Rt△ABC中,∠C=90°,AC=6,AB=10.以点A为圆心,适当长为半径画弧,分别交 AC,AB于点M,N,再分别以点 M,N为圆心,大于 MN的长为半径画弧,两弧在∠CAB的内部相交于点 P,画射线AP与BC交于点D,DE⊥AB,垂足为E,则下列结论错误的是 ( )
A.∠CAD=∠BAD
B. CD=DE
D. CD:BD=3:5
10.[2022·江苏连云港]已知∠A 的补角为60°,则∠A= °.
11.[2023·内蒙古通辽]将一副三角尺按如图所示的方式放置,其中AB∥DE,则∠CDF= °.
12.[2023·吉林]如图,在△ABC 中,AB=AC,分别以点 B 和点 C 为圆心,大于 BC的长为半径画弧,两弧交于点 D,作直线AD交BC于点 E.若∠BAC=110°,则∠BAE= °.
13.[2023·内蒙古赤峰]已知:如图,点 M在∠AOB 的边OA 上.
求作:射线 MN,使 MN∥OB,且点 N在∠AOB的平分线上.
作法:①以点O为圆心,适当长为半径画弧,分别交射线OA,OB于点C,D.
②分别以点C,D为圆心,大于 CD的长为半径画弧,两弧在∠AOB 的内部相交于点 P.
③画射线OP.
④以点 M 为圆心,OM 的长为半径画弧,交射线OP 于点N.
⑤画射线 MN.射线MN 即为所求.
(1)用尺规作图,依作法补全图形(保留作图痕迹);
(2)根据以上作图过程,完成下面的证明(括号内填写推理依据).
证明:∵OP平分∠AOB,
∴∠AON= .
∵OM=MN,
∴∠AON= ( ),
∴∠BON=∠ONM,
∴MN∥OB( ).
第十二章 线段与角、相交线与平行线
1. D ∵AB∥CD,
∴∠BCD=∠ABC=137°.
2. B ∵∠AOD=∠1=80°,
∴∠AOE=∠AOD-∠2=80°-30°=50°.
3. B ∵AB∥DC,∴∠B+∠C=180°.
∵BC∥DE,∴∠C=∠D,
∴∠B+∠D=180°.
∵∠B=145°,∴∠D=35°.
4. C ∵DE垂直平分AB,交 BC于点D,
∴AD=DB.
∵△ACD的周长为50cm,
∴AC+AD+CD=AC+CD+DB=AC+BC=50cm.
5. A
6. C A.平行四边形不一定是轴对称图形,故选项A是假命题,不符合题意;
B.对角线互相垂直的平行四边形是菱形,故选项B是假命题,不符合题意;
C.到一条线段两个端点距离相等的点,在这条线段的垂直平分线上,故选项C是真命题,符合题意;
D.在△ABC中,当∠A:∠B:∠C=3:4:5时,∠C=75°,所以△ABC不是直角三角形,故选项D是假命题,不符合题意.
7. B 连接AB(图略),将点 A 平移到点 P,即为向上平移3个单位长度,将点 B向上平移3个单位长度后,点 B不在PQ 上,
∴AB与PQ 不平行,故选项 A错误;
连接BC(图略),将点 B平移到点 P,即为向上平移4个单位长度,再向右平移1个单位长度(或向右平移1个单位长度,再向上平移4个单位长度),将点C按此方式平移后,点C在PQ上,
∴BC∥PQ,故选项B正确;
连接BD,AD,并反向延长与 PQ相交(图略),根据垂直的意义,知BD,AD与PQ不垂直,故选项C,D错误.
8. C 如图.
∵AB∥OF,∴∠1+∠OFB=180°.
∵∠1=155°,∴∠OFB=25°.
∵∠POF=∠2=30°,
9. C 由作图可得,AP平分∠BAC,
∴∠CAD=∠BAD,故选项 A不符合题意.
∵∠C=90°,DE⊥AB,
∴CD=DE,故选项B不符合题意.
在Rt△ABC中,AC=6,AB=10,
即6×8=6CD+10CD,
解得CD=3,
故选项C符合题意.
∵BD=BC-CD=8-3=5,
∴CD: BD=3:5,故选项D不符合题意.
1.[2023·广东]如图,街道AB与CD 平行,拐角∠ABC=137°,则拐角∠BCD=( )
A.43° B.53° C.107° D.137°
2.[2023·河南]如图,直线AB,CD相交于点O,若∠1=80°,∠2=30°,则∠AOE的度数为 ( )
A.30° B.50° C.60° D.80°
3.[2024·陕西]如图,AB∥DC,BC∥DE,∠B=145°,则∠D 的度数为 ( )
A.25° B.35° C.45° D.55°
4.[2024·四川凉山州]如图,在 Rt△ABC中,∠ACB=90°,DE 垂直平分AB,交BC于点D.若△ACD 的周长为50cm,则AC+BC= ( )
A.25 cm B.45 cm
C.50cm D.55 cm
5.[2022·江苏常州]如图,斑马线的作用是为了引导行人安全地通过马路.小丽觉得行人沿垂直马路的方向走过斑马线更为合理,这一想法体现的数学依据是( )
A.垂线段最短
B.两点确定一条直线
C.过一点有且只有一条直线与已知直线垂直
D.过直线外一点有且只有一条直线与已知直线平行
6.[2023·四川达州]下列命题中,是真命题的是 ( )
A.平行四边形是轴对称图形
B.对角线互相垂直的四边形是菱形
C.到一条线段两个端点距离相等的点,在这条线段的垂直平分线上
D.在△ABC 中,若∠A: ∠B: ∠C=3:4:5,则△ABC是直角三角形
7.[2023·江苏苏州]如图,在正方形网格内,线段 PQ的两个端点都在格点上,网格内另有A,B,C,D四个格点.下列四个结论中,正确的是 ( )
A.连接AB,则AB∥PQ
B.连接BC,则BC∥PQ
C.连接BD,则BD⊥PQ
D.连接AD,则AD⊥PQ
8.[2023·山西]如图,一束平行于主光轴的光线经凸透镜折射后,其折射光线与一束经过光心O的光线相交于点 P,F为焦点.若∠1=155°,∠2=30°,则∠3的度数为 ( )
A.45° B.50° C.55° D.60°
9.[2023·四川南充]如图,在 Rt△ABC中,∠C=90°,AC=6,AB=10.以点A为圆心,适当长为半径画弧,分别交 AC,AB于点M,N,再分别以点 M,N为圆心,大于 MN的长为半径画弧,两弧在∠CAB的内部相交于点 P,画射线AP与BC交于点D,DE⊥AB,垂足为E,则下列结论错误的是 ( )
A.∠CAD=∠BAD
B. CD=DE
D. CD:BD=3:5
10.[2022·江苏连云港]已知∠A 的补角为60°,则∠A= °.
11.[2023·内蒙古通辽]将一副三角尺按如图所示的方式放置,其中AB∥DE,则∠CDF= °.
12.[2023·吉林]如图,在△ABC 中,AB=AC,分别以点 B 和点 C 为圆心,大于 BC的长为半径画弧,两弧交于点 D,作直线AD交BC于点 E.若∠BAC=110°,则∠BAE= °.
13.[2023·内蒙古赤峰]已知:如图,点 M在∠AOB 的边OA 上.
求作:射线 MN,使 MN∥OB,且点 N在∠AOB的平分线上.
作法:①以点O为圆心,适当长为半径画弧,分别交射线OA,OB于点C,D.
②分别以点C,D为圆心,大于 CD的长为半径画弧,两弧在∠AOB 的内部相交于点 P.
③画射线OP.
④以点 M 为圆心,OM 的长为半径画弧,交射线OP 于点N.
⑤画射线 MN.射线MN 即为所求.
(1)用尺规作图,依作法补全图形(保留作图痕迹);
(2)根据以上作图过程,完成下面的证明(括号内填写推理依据).
证明:∵OP平分∠AOB,
∴∠AON= .
∵OM=MN,
∴∠AON= ( ),
∴∠BON=∠ONM,
∴MN∥OB( ).
第十二章 线段与角、相交线与平行线
1. D ∵AB∥CD,
∴∠BCD=∠ABC=137°.
2. B ∵∠AOD=∠1=80°,
∴∠AOE=∠AOD-∠2=80°-30°=50°.
3. B ∵AB∥DC,∴∠B+∠C=180°.
∵BC∥DE,∴∠C=∠D,
∴∠B+∠D=180°.
∵∠B=145°,∴∠D=35°.
4. C ∵DE垂直平分AB,交 BC于点D,
∴AD=DB.
∵△ACD的周长为50cm,
∴AC+AD+CD=AC+CD+DB=AC+BC=50cm.
5. A
6. C A.平行四边形不一定是轴对称图形,故选项A是假命题,不符合题意;
B.对角线互相垂直的平行四边形是菱形,故选项B是假命题,不符合题意;
C.到一条线段两个端点距离相等的点,在这条线段的垂直平分线上,故选项C是真命题,符合题意;
D.在△ABC中,当∠A:∠B:∠C=3:4:5时,∠C=75°,所以△ABC不是直角三角形,故选项D是假命题,不符合题意.
7. B 连接AB(图略),将点 A 平移到点 P,即为向上平移3个单位长度,将点 B向上平移3个单位长度后,点 B不在PQ 上,
∴AB与PQ 不平行,故选项 A错误;
连接BC(图略),将点 B平移到点 P,即为向上平移4个单位长度,再向右平移1个单位长度(或向右平移1个单位长度,再向上平移4个单位长度),将点C按此方式平移后,点C在PQ上,
∴BC∥PQ,故选项B正确;
连接BD,AD,并反向延长与 PQ相交(图略),根据垂直的意义,知BD,AD与PQ不垂直,故选项C,D错误.
8. C 如图.
∵AB∥OF,∴∠1+∠OFB=180°.
∵∠1=155°,∴∠OFB=25°.
∵∠POF=∠2=30°,
9. C 由作图可得,AP平分∠BAC,
∴∠CAD=∠BAD,故选项 A不符合题意.
∵∠C=90°,DE⊥AB,
∴CD=DE,故选项B不符合题意.
在Rt△ABC中,AC=6,AB=10,
即6×8=6CD+10CD,
解得CD=3,
故选项C符合题意.
∵BD=BC-CD=8-3=5,
∴CD: BD=3:5,故选项D不符合题意.
同课章节目录
