【河南专用】2025年中考数学全真模拟卷 (含详解)
文档属性
| 名称 | 【河南专用】2025年中考数学全真模拟卷 (含详解) |  | |
| 格式 | docx | ||
| 文件大小 | 2.1MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 通用版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2025-05-28 18:11:20 | ||
图片预览




文档简介
2025届中考数学全真模拟卷 【河南专用】
【满分120分 考试时间120分钟】
一、选择题(本大题共10小题,每小题3分,共30分.在每小题给出的四个选项中,只有一项是符合题目要求的)
1.[2024年内蒙古中考真题]的绝对值是( )
A. B.10 C. D.
2.[2024年江西中考真题]“长征是宣言书,长征是宣传队,长征是播种机”.二万五千里长征是中国历史上的伟大壮举,也是人类史上的奇迹.将25000用科学记数法可表示为( )
A. B. C. D.
3.[2024年吉林长春中考真题]下列运算一定正确的是( )
A. B. C. D.
4.[2024年山东东营中考真题]已知,直线,把一块含有角的直角三角板如图放置,,三角板的斜边所在直线交b于点A,则( )
A. B. C. D.
5.[2024年山东枣庄中考真题]某校课外活动期间开展跳绳、踢毽子、韵律操三项活动,甲、乙两位同学各自任选其中一项参加,则他们选择同一项活动的概率是( )
A. B. C. D.
6.[2024年黑龙江齐齐哈尔中考真题]如果关于x的分式方程的解是负数,那么实数m的取值范围是( )
A.且 B. C. D.且
7.[2024年辽宁中考真题]如图,在平面直角坐标系中,菱形的顶点A在x轴负半轴上,顶点B在直线上,若点B的横坐标是8,为点C的坐标为( )
A. B. C. D.
8.[2024年四川宜宾中考真题]如图,内接于,为的直径,AD平分交于D.则的值为( )
A. B. C. D.
9.[2024年四川宜宾中考真题]如图,等腰三角形ABC中,,反比例函数的图象经过点A,B及AC的中点M,轴,AB与y轴交于点N,则的值为( )
A. B. C. D.
10.[2024年四川资阳中考真题]已知二次函数与的图像均过点和坐标原点O,这两个函数在时形成的封闭图像如图所示,P为线段的中点,过点P且与x轴不重合的直线与封闭图像交于B,C两点.给出下列结论:
①;
②;
③以O,A,B,C为顶点的四边形可以为正方形;
④若点B的横坐标为1,点Q在y轴上(Q,B,C三点不共线),则周长的最小值为.
其中,所有正确结论的个数是( )
A.1 B.2 C.3 D.4
二、填空题(本大题共5小题,每小题3分,共15分.请把答案填在题中横线上)
11.[2024年黑龙江牡丹江中考真题]函数中,自变量x的取值范围是______________.
12.[2024年山东烟台中考真题]若一元二次方程的两根为m,n,则的值为___________.
13.[2024年山西中考真题]黄金分割是汉字结构最基本的规律.借助如图的正方形习字格书写的汉字“晋”端庄稳重、舒展美观.已知一条分制线的端点A,B分别在习字格的边MN,PQ上,且,“晋”字的笔画“、”的位置在AB的黄金分割点C处,且.若,则BC的长为________(结果保留根号).
14.[2024年四川资阳中考真题]如图,在矩形中,,.以点A为圆心,长为半径作弧交于点E,再以为直径作半圆,与交于点F,则图中阴影部分的面积为__________.
15.[2024年山西中考真题]如图,在中,AC为对角线,于点E,点F是AE延长线上一点,且,线段,的延长线交于点G.若,,,则BG的长为________.
三、解答题(本大题共8小题,共75分.解答应写出必要的文字说明,证明过程或演算步骤)
16.(10分)[2024年四川绵阳中考真题](1)计算:;
(2)先化简,再求值:,其中.
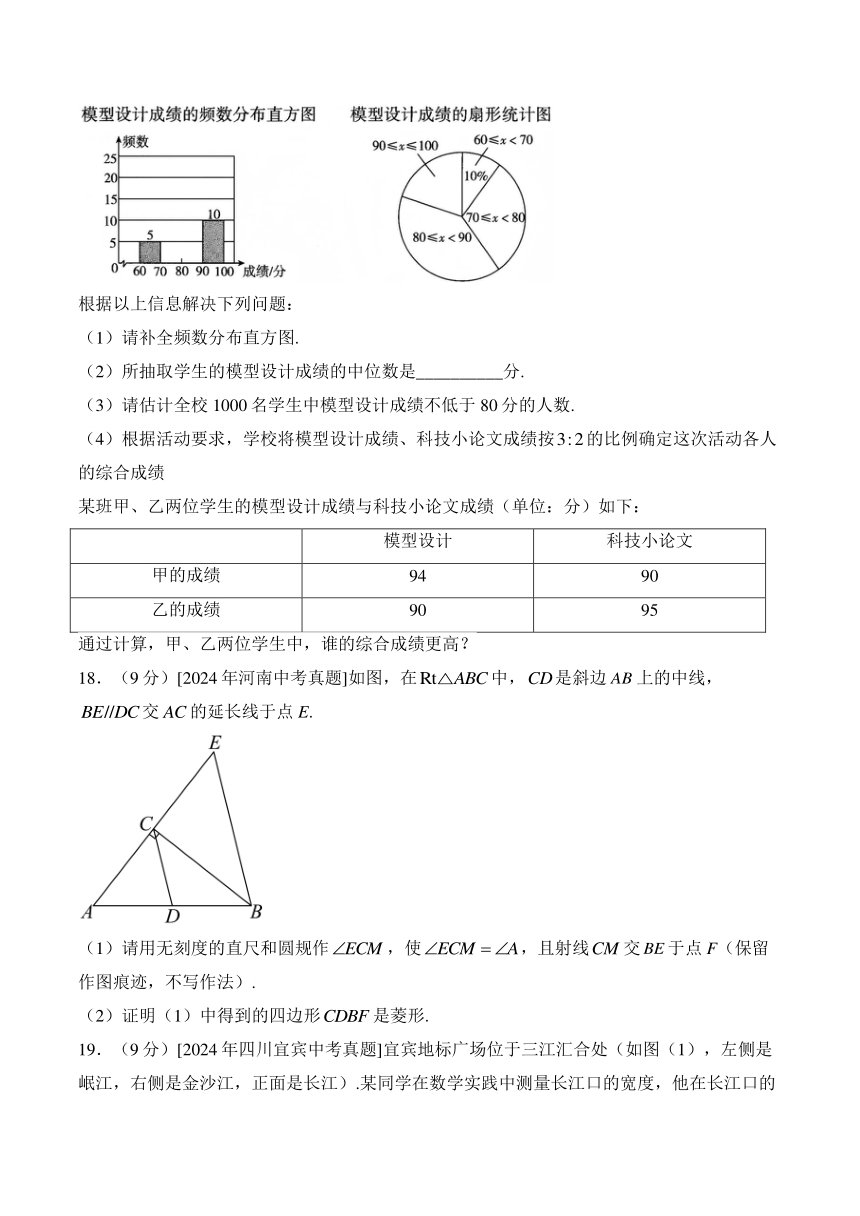
17.(9分)[2024年山东枣庄中考真题]某学校开展了“校园科技节”活动,活动包含模型设计、科技小论文两个项目.为了解学生的模型设计水平,从全校学生的模型设计成绩中随机抽取部分学生的模型设计成绩(成绩为百分制,用x表示),并将其分成如下四组:,,,.
下面给出了部分信息:
的成绩为:81,81,82,82,83,83,84,84,84,85,86,86,86,87,88,88,88,89,89,89.
根据以上信息解决下列问题:
(1)请补全频数分布直方图.
(2)所抽取学生的模型设计成绩的中位数是__________分.
(3)请估计全校1000名学生中模型设计成绩不低于80分的人数.
(4)根据活动要求,学校将模型设计成绩、科技小论文成绩按的比例确定这次活动各人的综合成绩
某班甲、乙两位学生的模型设计成绩与科技小论文成绩(单位:分)如下:
模型设计 科技小论文
甲的成绩 94 90
乙的成绩 90 95
通过计算,甲、乙两位学生中,谁的综合成绩更高?
18.(9分)[2024年河南中考真题]如图,在中,是斜边上的中线,交的延长线于点E.
(1)请用无刻度的直尺和圆规作,使,且射线交于点F(保留作图痕迹,不写作法).
(2)证明(1)中得到的四边形是菱形.
19.(9分)[2024年四川宜宾中考真题]宜宾地标广场位于三江汇合处(如图(1),左侧是岷江,右侧是金沙江,正面是长江).某同学在数学实践中测量长江口的宽度,他在长江口的两岸选择两个标点C,D,在地标广场上选择两个观测点A,B(点A,B,C,D在同一平面内,且).如图(2)所示,在点A处测得点C在北偏西方向上,测得点D在北偏东方向上,在点B处测得点C在北偏西方向上,测得点D在北偏东方向上,测得米.求长江口的宽度CD的值.(结果精确到1米.参考数据:,,,,,)
20.(9分)[2024年陕西中考真题]一条河上横跨着一座宏伟壮观的悬索桥.桥梁的缆索与缆索均呈抛物线型,桥塔与桥塔均垂直于桥面,如图所示,以O为原点,以直线为x轴,以桥塔所在直线为y轴,建立平面直角坐标系.
已知:缆索所在抛物线与缆索所在抛物线关于y轴对称,桥塔与桥塔之间的距离,,缆索的最低点P到的距离(桥塔的粗细忽略不计)
(1)求缆索所在抛物线的函数表达式;
(2)点E在缆索上,,且,,求的长.
21.(9分)[2024年江苏淮安中考真题]如图,在平面直角坐标系中,一次函数的图像与x轴、y轴分别交于点A、B,与反比例函数的图像交于点C,已知点A坐标为,点C坐标为.
(1)求反比例函数及一次函数的表达式;
(2)点D在线段上,过点D且平行于x轴的直线交于点E,交反比例函数图像于点F,当时,求点F的坐标.
22.(10分)[2024年江苏淮安中考真题]如图,在中,,以为直径作交于点D,过点D作,垂足为E,延长交的延长线于点F.
(1)求证:为的切线;
(2)若,,求的值.
23.(10分)[2024年山东枣庄中考真题]一副三角板分别记作和,其中,,,.作于点M,于点N,如图(1).
(1)求证:.
(2)在同一平面内,将图(1)中的两个三角形按如图(2)所示的方式放置,点C与点E重合记为C,点A与点D重合,将图(2)中的绕C按顺时针方向旋转后,延长BM交直线DF于点P.
①当时,如图(3),求证:四边形CNPM为正方形.
②当时,写出线段MP,DP,CD的数量关系,并证明;当时,直接写出线段MP,DP,CD的数量关系.
参考答案
1.答案:A
解析:因为为负数,
所以的绝对值为,
故选A.
2.答案:C
解析:,故选C.
3.答案:C
解析:A.,故本选项不符合题意;
B.,故本选项不符合题意;
C.,故本选项符合题意;
D.,故本选项不符合题意;
故选:C.
4.答案:B
解析:,
,
,
故选:B.
5.答案:C
解析:把跳绳、踢毽子、韵律操分别记为A,B,C,根据题意,画树状图如下:
由树状图可知,共有9种等可能的结果,其中甲、乙两位同学恰好选择同一项活动的结果有3种,故所求概率为.故选C.
6.答案:A
解析:,
,
,
,
,
关于x的分式方程的解是负数,
且,
解得:且,
故选: A.
7.答案:B
解析:过点B作轴,垂足为点D,
顶点B在直线上,点B的横坐标是8,
,即,
,
轴,
由勾股定理得:,
四边形是菱形,
,轴,
将点B向左平移10个单位得到点C,
点,
故选:B.
8.答案:A
解析:如图,连接,.
是的直径,.
平分,,,.
将绕点D逆时针旋转,得到,
,A,B,三点共线,.
由旋转可知,,
在等腰直角三角形中,,.故选A.
9.答案:B
解析:过点A作BC的垂线,垂足为点D,设BC与y轴交于点E,
如图.在等腰三角形ABC中,,则D是BC的中点,
设,,则,
.
的中点为M,.
点M在反比例函数图象上,,
(不合题意,已舍去).
由题可知,,.故选B.
10.答案:D
解析:①二次函数与的图像均过点和坐标原点O,P为线段的中点,
,两个函数的对称轴均为直线,
即,
解得:,故①正确;
②如图,过点B作交x轴于点D,过点C作交x轴于点E,
,
由函数的对称性可知,
在和中,
,
,
,故正确②;
③当点B、C分别在两个函数的顶点上时,,点B、C的横坐标均为2,
由①可知两个函数的解析式分别为,,
,,
,
点,
,
,
由,
此时以O,A,B,C为顶点的四边形为正方形,故③正确;
④作点B关于y轴的对称点,连接交y轴于点Q,此时周长的最小,最小值为,
点B的横坐标为1,
,点C的横坐标为3,
,,
,,
周长的最小值为,故正确④;
故选:D.
11.答案:且
解析:根据题意得:且,
解得且.
故答案为:且.
12.答案:6
解析:一元二次方程的两根为m,n,,,,.
13.答案:
解析:四边形是正方形,
,
又,
,
,
四边形是矩形,
,
又,
,
故答案为:.
14.答案:
解析:以点A为圆心,长为半径作弧交于点E,,,
,
以为直径作半圆时,圆心为点E,
设弓形,连接,,即,如图:
为等边三角形,
,
故阴影部分面积为,
代入数值可得,
故答案为.
15.答案:
解析:在中,,,可得,,
四边形是平行四边形,
,,
,
(依据:等角对等边).
设,则,
在中,由勾股定理,得,即,解得,即,
如图,过点G作,垂足为H,则,
,(依据:相似三角形的对应边成比例).
,.
设,则,,,
,.
16.答案:(1)0
(2);
解析:(1)
;
(2)
,
当时,原式.
17.答案:(1)图见解析
(2)83
(3)600人
(4)甲的综合成绩更高
解析:(1)补全频数分布直方图如图.
(2)将所抽取50名学生的成绩按照从小到大排列,位于第25,26位的数据分别是83,83,
中位数为.
(3)(人).
答:估计全校1000名学生中模型设计成绩不低于80分的人数为600人.
(4)甲的综合成绩为(分),
乙的综合成绩为(分),
,
甲的综合成绩更高.
18.答案:(1)见解析
(2)见解析
解析:(1)如图,即为所求.
(2)证明:由(1),得,
.
,
四边形CDBF是平行四边形,
是斜边上的中线,
,
四边形是菱形.
19.答案:1200米
解析:如图,分别过点A,B作CD的垂线,垂足分别为点E,F,则.
由,,,可证得四边形ABFE是矩形,
.
设.
在中,,
.
在中,,
.
在中,,
.
,
,
解得,
.
答:长江口的宽度CD的值约为1200米.
20.答案:(1)
(2)的长为
解析:(1)由题意得顶点P的坐标为,点A的坐标为,
设缆索所在抛物线的函数表达式为,
把代入得,
解得,
缆索所在抛物线的函数表达式为;
(2)缆索所在抛物线与缆索所在抛物线关于y轴对称,
缆索所在抛物线的函数表达式为,
,
把代入得,,
解得,,
或,
,
的长为.
21.答案:(1)
(2)
解析:(1)把点代入得:,
解得,
反比例函数的表达式为,
把点,点代入得,
,
解得,
一次函数的表达式为;
(2)设,
平行于x轴,
,
,
,
,
解得,
,
点F的纵坐标为,
把代入得,,
点F的坐标为.
22.答案:(1)证明见解析
(2)
解析:(1)证明:连接,,如图,
为的直径,
,
,
,
点D为的中点,
点O为的中点,
为的中位线,
,
,
,
,
,
,
为的半径,D为的外端点,
为的切线;
(2)如上图,
,,,
由勾股定理,得,
由(1)知,
,
,
,,,
,
解得,,
,
在中,
由勾股定理,得,
,
,
.
23.答案:(1)证明见解析
(2)①证明见解析
②当时,;当时,
解析:(1)证明:,,
,.
,.
,,.
,
.
(2)①证明:,,
四边形CNPM为矩形.
由(1)得,
又,,
四边形PMCN是正方形.
②当时,.
证明:如图(1),连接MN.
,.
又,
.
.
又,,
.
当时,.
当时,如图(2),连接CP,
由①得.
,,
,
,
.
又,
,即.
【满分120分 考试时间120分钟】
一、选择题(本大题共10小题,每小题3分,共30分.在每小题给出的四个选项中,只有一项是符合题目要求的)
1.[2024年内蒙古中考真题]的绝对值是( )
A. B.10 C. D.
2.[2024年江西中考真题]“长征是宣言书,长征是宣传队,长征是播种机”.二万五千里长征是中国历史上的伟大壮举,也是人类史上的奇迹.将25000用科学记数法可表示为( )
A. B. C. D.
3.[2024年吉林长春中考真题]下列运算一定正确的是( )
A. B. C. D.
4.[2024年山东东营中考真题]已知,直线,把一块含有角的直角三角板如图放置,,三角板的斜边所在直线交b于点A,则( )
A. B. C. D.
5.[2024年山东枣庄中考真题]某校课外活动期间开展跳绳、踢毽子、韵律操三项活动,甲、乙两位同学各自任选其中一项参加,则他们选择同一项活动的概率是( )
A. B. C. D.
6.[2024年黑龙江齐齐哈尔中考真题]如果关于x的分式方程的解是负数,那么实数m的取值范围是( )
A.且 B. C. D.且
7.[2024年辽宁中考真题]如图,在平面直角坐标系中,菱形的顶点A在x轴负半轴上,顶点B在直线上,若点B的横坐标是8,为点C的坐标为( )
A. B. C. D.
8.[2024年四川宜宾中考真题]如图,内接于,为的直径,AD平分交于D.则的值为( )
A. B. C. D.
9.[2024年四川宜宾中考真题]如图,等腰三角形ABC中,,反比例函数的图象经过点A,B及AC的中点M,轴,AB与y轴交于点N,则的值为( )
A. B. C. D.
10.[2024年四川资阳中考真题]已知二次函数与的图像均过点和坐标原点O,这两个函数在时形成的封闭图像如图所示,P为线段的中点,过点P且与x轴不重合的直线与封闭图像交于B,C两点.给出下列结论:
①;
②;
③以O,A,B,C为顶点的四边形可以为正方形;
④若点B的横坐标为1,点Q在y轴上(Q,B,C三点不共线),则周长的最小值为.
其中,所有正确结论的个数是( )
A.1 B.2 C.3 D.4
二、填空题(本大题共5小题,每小题3分,共15分.请把答案填在题中横线上)
11.[2024年黑龙江牡丹江中考真题]函数中,自变量x的取值范围是______________.
12.[2024年山东烟台中考真题]若一元二次方程的两根为m,n,则的值为___________.
13.[2024年山西中考真题]黄金分割是汉字结构最基本的规律.借助如图的正方形习字格书写的汉字“晋”端庄稳重、舒展美观.已知一条分制线的端点A,B分别在习字格的边MN,PQ上,且,“晋”字的笔画“、”的位置在AB的黄金分割点C处,且.若,则BC的长为________(结果保留根号).
14.[2024年四川资阳中考真题]如图,在矩形中,,.以点A为圆心,长为半径作弧交于点E,再以为直径作半圆,与交于点F,则图中阴影部分的面积为__________.
15.[2024年山西中考真题]如图,在中,AC为对角线,于点E,点F是AE延长线上一点,且,线段,的延长线交于点G.若,,,则BG的长为________.
三、解答题(本大题共8小题,共75分.解答应写出必要的文字说明,证明过程或演算步骤)
16.(10分)[2024年四川绵阳中考真题](1)计算:;
(2)先化简,再求值:,其中.
17.(9分)[2024年山东枣庄中考真题]某学校开展了“校园科技节”活动,活动包含模型设计、科技小论文两个项目.为了解学生的模型设计水平,从全校学生的模型设计成绩中随机抽取部分学生的模型设计成绩(成绩为百分制,用x表示),并将其分成如下四组:,,,.
下面给出了部分信息:
的成绩为:81,81,82,82,83,83,84,84,84,85,86,86,86,87,88,88,88,89,89,89.
根据以上信息解决下列问题:
(1)请补全频数分布直方图.
(2)所抽取学生的模型设计成绩的中位数是__________分.
(3)请估计全校1000名学生中模型设计成绩不低于80分的人数.
(4)根据活动要求,学校将模型设计成绩、科技小论文成绩按的比例确定这次活动各人的综合成绩
某班甲、乙两位学生的模型设计成绩与科技小论文成绩(单位:分)如下:
模型设计 科技小论文
甲的成绩 94 90
乙的成绩 90 95
通过计算,甲、乙两位学生中,谁的综合成绩更高?
18.(9分)[2024年河南中考真题]如图,在中,是斜边上的中线,交的延长线于点E.
(1)请用无刻度的直尺和圆规作,使,且射线交于点F(保留作图痕迹,不写作法).
(2)证明(1)中得到的四边形是菱形.
19.(9分)[2024年四川宜宾中考真题]宜宾地标广场位于三江汇合处(如图(1),左侧是岷江,右侧是金沙江,正面是长江).某同学在数学实践中测量长江口的宽度,他在长江口的两岸选择两个标点C,D,在地标广场上选择两个观测点A,B(点A,B,C,D在同一平面内,且).如图(2)所示,在点A处测得点C在北偏西方向上,测得点D在北偏东方向上,在点B处测得点C在北偏西方向上,测得点D在北偏东方向上,测得米.求长江口的宽度CD的值.(结果精确到1米.参考数据:,,,,,)
20.(9分)[2024年陕西中考真题]一条河上横跨着一座宏伟壮观的悬索桥.桥梁的缆索与缆索均呈抛物线型,桥塔与桥塔均垂直于桥面,如图所示,以O为原点,以直线为x轴,以桥塔所在直线为y轴,建立平面直角坐标系.
已知:缆索所在抛物线与缆索所在抛物线关于y轴对称,桥塔与桥塔之间的距离,,缆索的最低点P到的距离(桥塔的粗细忽略不计)
(1)求缆索所在抛物线的函数表达式;
(2)点E在缆索上,,且,,求的长.
21.(9分)[2024年江苏淮安中考真题]如图,在平面直角坐标系中,一次函数的图像与x轴、y轴分别交于点A、B,与反比例函数的图像交于点C,已知点A坐标为,点C坐标为.
(1)求反比例函数及一次函数的表达式;
(2)点D在线段上,过点D且平行于x轴的直线交于点E,交反比例函数图像于点F,当时,求点F的坐标.
22.(10分)[2024年江苏淮安中考真题]如图,在中,,以为直径作交于点D,过点D作,垂足为E,延长交的延长线于点F.
(1)求证:为的切线;
(2)若,,求的值.
23.(10分)[2024年山东枣庄中考真题]一副三角板分别记作和,其中,,,.作于点M,于点N,如图(1).
(1)求证:.
(2)在同一平面内,将图(1)中的两个三角形按如图(2)所示的方式放置,点C与点E重合记为C,点A与点D重合,将图(2)中的绕C按顺时针方向旋转后,延长BM交直线DF于点P.
①当时,如图(3),求证:四边形CNPM为正方形.
②当时,写出线段MP,DP,CD的数量关系,并证明;当时,直接写出线段MP,DP,CD的数量关系.
参考答案
1.答案:A
解析:因为为负数,
所以的绝对值为,
故选A.
2.答案:C
解析:,故选C.
3.答案:C
解析:A.,故本选项不符合题意;
B.,故本选项不符合题意;
C.,故本选项符合题意;
D.,故本选项不符合题意;
故选:C.
4.答案:B
解析:,
,
,
故选:B.
5.答案:C
解析:把跳绳、踢毽子、韵律操分别记为A,B,C,根据题意,画树状图如下:
由树状图可知,共有9种等可能的结果,其中甲、乙两位同学恰好选择同一项活动的结果有3种,故所求概率为.故选C.
6.答案:A
解析:,
,
,
,
,
关于x的分式方程的解是负数,
且,
解得:且,
故选: A.
7.答案:B
解析:过点B作轴,垂足为点D,
顶点B在直线上,点B的横坐标是8,
,即,
,
轴,
由勾股定理得:,
四边形是菱形,
,轴,
将点B向左平移10个单位得到点C,
点,
故选:B.
8.答案:A
解析:如图,连接,.
是的直径,.
平分,,,.
将绕点D逆时针旋转,得到,
,A,B,三点共线,.
由旋转可知,,
在等腰直角三角形中,,.故选A.
9.答案:B
解析:过点A作BC的垂线,垂足为点D,设BC与y轴交于点E,
如图.在等腰三角形ABC中,,则D是BC的中点,
设,,则,
.
的中点为M,.
点M在反比例函数图象上,,
(不合题意,已舍去).
由题可知,,.故选B.
10.答案:D
解析:①二次函数与的图像均过点和坐标原点O,P为线段的中点,
,两个函数的对称轴均为直线,
即,
解得:,故①正确;
②如图,过点B作交x轴于点D,过点C作交x轴于点E,
,
由函数的对称性可知,
在和中,
,
,
,故正确②;
③当点B、C分别在两个函数的顶点上时,,点B、C的横坐标均为2,
由①可知两个函数的解析式分别为,,
,,
,
点,
,
,
由,
此时以O,A,B,C为顶点的四边形为正方形,故③正确;
④作点B关于y轴的对称点,连接交y轴于点Q,此时周长的最小,最小值为,
点B的横坐标为1,
,点C的横坐标为3,
,,
,,
周长的最小值为,故正确④;
故选:D.
11.答案:且
解析:根据题意得:且,
解得且.
故答案为:且.
12.答案:6
解析:一元二次方程的两根为m,n,,,,.
13.答案:
解析:四边形是正方形,
,
又,
,
,
四边形是矩形,
,
又,
,
故答案为:.
14.答案:
解析:以点A为圆心,长为半径作弧交于点E,,,
,
以为直径作半圆时,圆心为点E,
设弓形,连接,,即,如图:
为等边三角形,
,
故阴影部分面积为,
代入数值可得,
故答案为.
15.答案:
解析:在中,,,可得,,
四边形是平行四边形,
,,
,
(依据:等角对等边).
设,则,
在中,由勾股定理,得,即,解得,即,
如图,过点G作,垂足为H,则,
,(依据:相似三角形的对应边成比例).
,.
设,则,,,
,.
16.答案:(1)0
(2);
解析:(1)
;
(2)
,
当时,原式.
17.答案:(1)图见解析
(2)83
(3)600人
(4)甲的综合成绩更高
解析:(1)补全频数分布直方图如图.
(2)将所抽取50名学生的成绩按照从小到大排列,位于第25,26位的数据分别是83,83,
中位数为.
(3)(人).
答:估计全校1000名学生中模型设计成绩不低于80分的人数为600人.
(4)甲的综合成绩为(分),
乙的综合成绩为(分),
,
甲的综合成绩更高.
18.答案:(1)见解析
(2)见解析
解析:(1)如图,即为所求.
(2)证明:由(1),得,
.
,
四边形CDBF是平行四边形,
是斜边上的中线,
,
四边形是菱形.
19.答案:1200米
解析:如图,分别过点A,B作CD的垂线,垂足分别为点E,F,则.
由,,,可证得四边形ABFE是矩形,
.
设.
在中,,
.
在中,,
.
在中,,
.
,
,
解得,
.
答:长江口的宽度CD的值约为1200米.
20.答案:(1)
(2)的长为
解析:(1)由题意得顶点P的坐标为,点A的坐标为,
设缆索所在抛物线的函数表达式为,
把代入得,
解得,
缆索所在抛物线的函数表达式为;
(2)缆索所在抛物线与缆索所在抛物线关于y轴对称,
缆索所在抛物线的函数表达式为,
,
把代入得,,
解得,,
或,
,
的长为.
21.答案:(1)
(2)
解析:(1)把点代入得:,
解得,
反比例函数的表达式为,
把点,点代入得,
,
解得,
一次函数的表达式为;
(2)设,
平行于x轴,
,
,
,
,
解得,
,
点F的纵坐标为,
把代入得,,
点F的坐标为.
22.答案:(1)证明见解析
(2)
解析:(1)证明:连接,,如图,
为的直径,
,
,
,
点D为的中点,
点O为的中点,
为的中位线,
,
,
,
,
,
,
为的半径,D为的外端点,
为的切线;
(2)如上图,
,,,
由勾股定理,得,
由(1)知,
,
,
,,,
,
解得,,
,
在中,
由勾股定理,得,
,
,
.
23.答案:(1)证明见解析
(2)①证明见解析
②当时,;当时,
解析:(1)证明:,,
,.
,.
,,.
,
.
(2)①证明:,,
四边形CNPM为矩形.
由(1)得,
又,,
四边形PMCN是正方形.
②当时,.
证明:如图(1),连接MN.
,.
又,
.
.
又,,
.
当时,.
当时,如图(2),连接CP,
由①得.
,,
,
,
.
又,
,即.
同课章节目录
