小升初复习精讲精练《立体图形的表面积和体积》--苏教版(复习课件)
文档属性
| 名称 | 小升初复习精讲精练《立体图形的表面积和体积》--苏教版(复习课件) |

|
|
| 格式 | pptx | ||
| 文件大小 | 2.7MB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 苏教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2025-05-28 17:47:19 | ||
图片预览







文档简介
(共43张PPT)
(苏教版)六年级
下
图形与几何
立体图形的表面积和体积
01
教学目标
02
新知导入
03
任务一
04
任务二
05
拓展延伸
06
课堂练习
07
课堂小结
08
作业布置
09
板书设计
01
教学目标
1. 能准确区分表面积与体积(所占空间大小)的意义,并能举例说明生活中的应用场景。
2. 能熟练写出长方体、正方体、圆柱、圆锥等常见立体图形的表面积和体积公式,并解释公式中每个字母的含义。
3. 在计算中正确进行单位换算,并能分析结果是否符合实际。
立体图形的表面积和体积
长方体
正方体
表面积
体积
(长×宽+长×高+宽×高)×2
即S=2×(ab+ah+bh)
圆锥
01
复习导入
圆柱
表面积
体积
体积
表面积
体积
棱长×棱长×6 即S=6a
圆柱的侧面积+两个底面的面积
长 × 宽 × 高 V=abh
棱长×棱长×棱长 V=a
底面积×高 V=S底h=πr h
底面积×高÷3 V = Sh
02
任务一
学习任务一
知识梳理
a
h
b
下
右
左
前
后
上
长方体(或正方体)6个面的总面积,叫作它的表面积。
高
长
宽
高
长
宽
长方体的表面积:
(长×宽+长×高+宽×高)×2
即S=2×(ab+ah+bh)
长方体的表面积
02
知识梳理
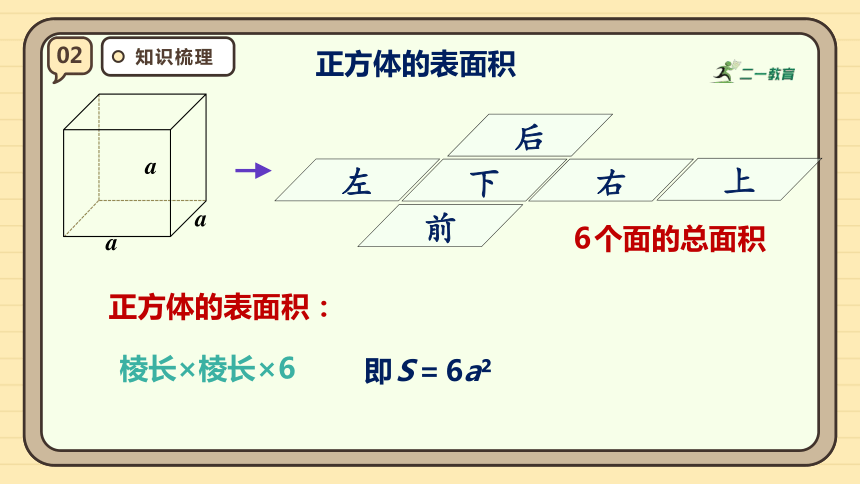
正方体的表面积:
棱长×棱长×6
a
a
a
后
前
左
右
上
下
即S=6a
6个面的总面积
02
知识梳理
正方体的表面积
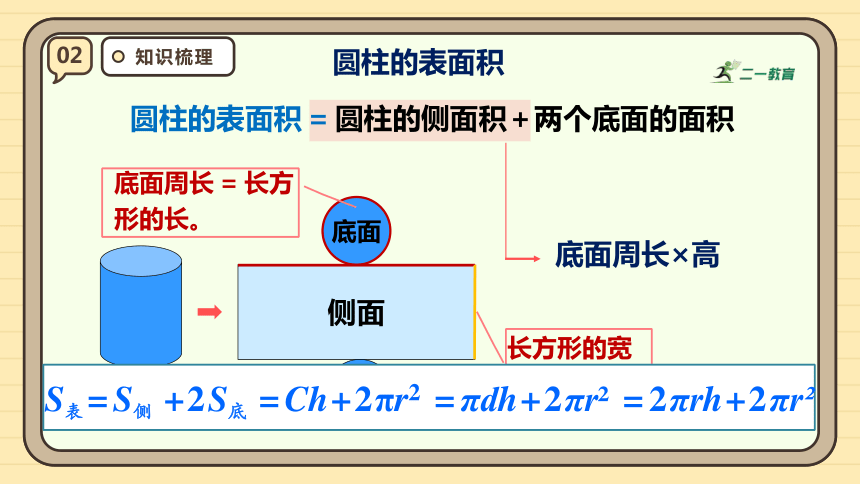
圆柱的表面积
圆柱的表面积=圆柱的侧面积+两个底面的面积
底面周长×高
侧面
底面
底面
底面周长=长方形的长。
长方形的宽
=圆柱的高。
S表=S侧 +2S底 =Ch+2πr2 =πdh+2πr =2πrh+2πr
02
知识梳理
体积和容积
立方厘米、立方分米、立方米。
升、毫升。
物体所占空间的大小叫作物体的体积。
容器所能容纳物体的体积叫作容器的容积。
计量容积,一般就用体积单位。计量液体的体积,通常用升或毫升作单位。
常用的体积单位:
常用的容积单位:
1粒花生米的
体积约1cm3
1盒牛奶大约有250毫升
02
知识梳理
体积单位间的进率:
1立方分米=1000立方厘米
升和毫升之间的进率是1000。
1升=1000毫升或1L=1000mL
升和毫升的进率:
1立方米=1000立方分米
每相邻单位之间的进率是1000。
1升=1立方分米
1毫升=1立方厘米
02
知识梳理
a
h
b
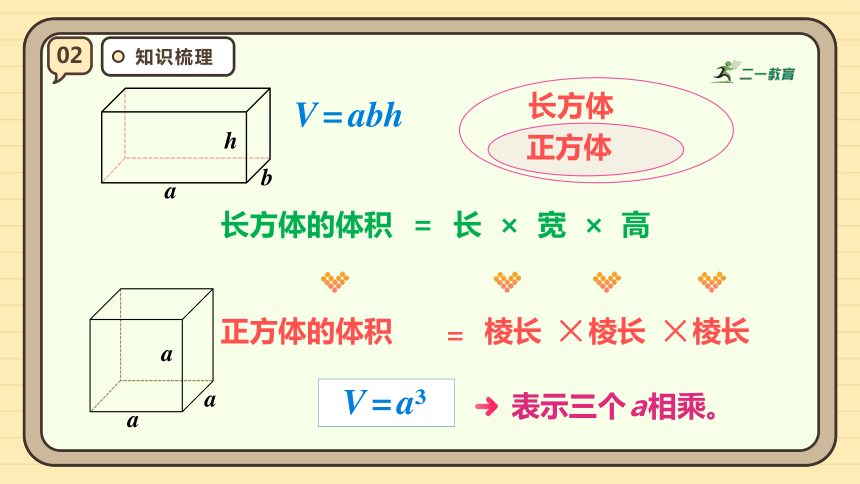
长方体的体积 = 长 × 宽 × 高
V=abh
长方体
正方体
正方体的体积
棱长
棱长
×
=
×
棱长
a
a
a
V=a
表示三个a相乘。
02
知识梳理
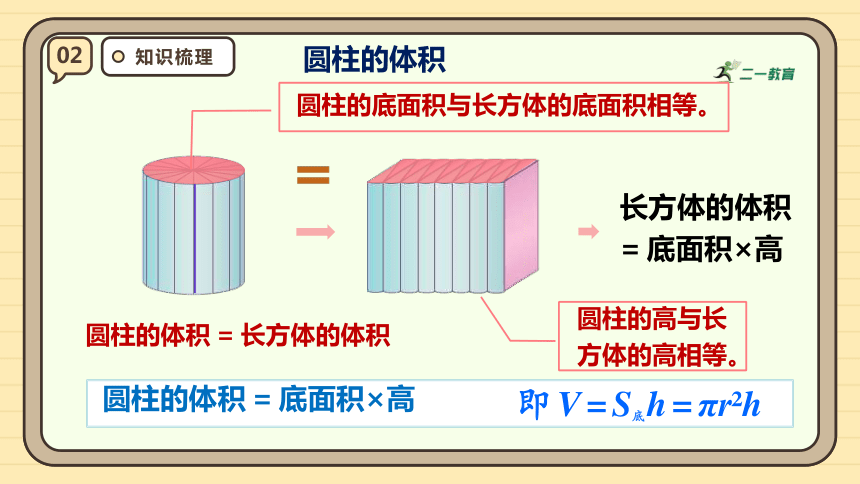
圆柱的体积
圆柱的底面积与长方体的底面积相等。
圆柱的高与长方体的高相等。
长方体的体积=底面积×高
圆柱的体积=长方体的体积
圆柱的体积=底面积×高
即V=S底h=πr h
02
知识梳理
圆柱和圆锥的体积
圆柱的体积
体积=底面积×高
圆心O
.
半径r
高 h
直径 d
侧面
.
体积=底面积×高÷3
.
半径r
高 h
侧面
底面
圆心O
.
圆锥的体积
圆锥的体积等于与它等底等高的圆柱体积的三分之一。
02
知识梳理
V=Sh
V= Sh
1
3
V=____
V=____
V=____
V=____
abh
a3
Sh
Sh
求物体的体积是从物体的外部来测量相关数据的,求物体的容积是从物体的内部来测量相关数据的。
V=____
Sh
02
知识梳理
在容器中装满水,把不规则物体完全浸入水中,溢出水的体积就是不规则物体的体积。
在粗细均匀的容器中倒入一定量的水,把不规则物体完全浸入水中,上升的水的体积就是不规则物体的体积。
利用体积不变的特征,把不规则物体转化成规则物体再进行计算。
溢出法
升高法
转化法
求不规则物体体积的方法
02
知识梳理
上升的水的体积就是鹅卵石的体积。
用“底面积×上升的高度”来计算。
怎样测量出一块拳头大的鹅卵石的体积?
02
知识梳理
03
任务二
学习任务二
典型例题
1.计算下面各图的表面积和体积。(图中单位:cm)
表面积:
(15×10+8×10+15×8)×2=700(cm2)
体积:
15×10×8=1200(cm3)
04
例题讲解
表面积:
6×10×10=600(cm2)
体积:
10×10×10=1000(cm3)
1.计算下面各图的表面积和体积。(图中单位:cm)
04
例题讲解
表面积:
2×3.14×42+3.14×8×12
=401.92(cm2)
体积:
3.14×42×12=602.88(cm3)
1.计算下面各图的表面积和体积。(图中单位:cm)
04
例题讲解
2.下面这个容器一共能装多少毫升水?(容器壁的厚度
忽略不计。)
8×5×2+3.14×(4÷2)2×3
=117.68(dm3)
=117680(mL)
答:这个容器能装117680毫升水。
04
例题讲解
3.一块圆锥形橡皮泥,底面积是12平方厘米,高是6厘米,
如果把它捏成同样高的一个圆柱,那么该圆柱的底面积
是多少平方厘米?
圆柱的底面积=体积÷高
24÷6=4(平方厘米)
答:该圆柱的底面积是4平方厘米。
04
例题讲解
圆锥体积=底面积×高×
1
3
12×6× =24(立方厘米)
1
3
4.一条水渠长800 m,横截面如下图。
(1)水渠的横截面积是多少平方米?
4×2.5=10(平方米)
答:水渠的横截面积是10平方米。
04
例题讲解
(2)水渠水深2 m,水在水渠中每分流动20 m,该水渠
每时的水流量是多少立方米?
2×4×20×60=9600(立方米)
答:该水渠每时的水流量是9600立方米。
04
例题讲解
1.求下面各圆柱的体积。
(1)底面积0.6平方米,高0.5平方米。
0.6×0.5=0.3(立方米)
(2)底面半径3厘米,高5厘米。
3.14×3 ×5=141.3(立方厘米)
(3)底面直径8米,高10米。
3.14×(8÷2) ×10=502.4(立方米)
----变式训练
05
课堂练习
2. 一台长方体形冰箱长0.6 m,宽0.5 m,高1.8 m。
(1)做这台冰箱的包装盒至少需要纸板多少平方米?
(2)这台冰箱占地面积是多少平方米?
(1)(0.6×0.5+0.6×1.8+0.5×1.8)×2=4.56(m2)
答:做这台冰箱的包装盒至少需要纸板4.56平方米。
(2)0.6×0.5=0.3(m2)
答:这台冰箱占地面积是0.3平方米。
----变式训练
05
课堂练习
3.一种空心的混凝土管道,内直径是40厘米,外直径是80厘米,长300厘米,求制作100节这种管道约需多少混凝土?
内半径是:40÷2=20(厘米)=0.2米
外半径是:80÷2=40(厘米)=0.4米
300厘米=3米
环形圆柱的体积:3.14×(0.4 -0.2 )×3=1.1304(立方米)
制作100节这种管道需要混凝土:
1.1304×100=113.04(立方米)
答:制作100节这种管道需要113.04立方米混凝土。
----变式训练
05
课堂练习
4.一种抽水机出水管的直径是1分米,管口水流的速度是每秒2米,1分钟能抽多少立方米?
1分米=0.1米
3.14×(0.1÷2) ×2=0.0157(立方米)
0.0157×60=0.942(立方米)
答:1分钟能抽0.942立方米。
----变式训练
05
课堂练习
5.用一根长24 cm的铁丝围一个长方体(或正方体)框架。在这个长方体的表面糊一层纸,怎样围框架用纸最多?
由题意可知,铁丝的长度就是长方体(或正方体)的棱长总和。长方体有4组长、宽、高,
24÷4=6(cm),
可以得出一组长、宽、高的和是6 cm。
求怎样围框架用纸最多,就是要使长方体(或正方体)的表面积最大。
----变式训练
05
课堂练习
06
任务四
学习任务四
培优拓展
1.将一个直角边分别为7厘米、9厘米的直角三角形,以一条直角边所在的直线为轴旋转,旋转后的圆锥的体积是多少?
7 cm
9 cm
13
3.14×92×7×-=593.46(cm3)
06
培优拓展
7 cm
9 cm
13
3.14×72×9×-=461.58(cm3)
593.46>461.58
答:以7厘米的直角边所在的直线为轴旋转,得到的圆锥的体积最大。
1.将一个直角边分别为7厘米、9厘米的直角三角形,以一条直角边所在的直线为轴旋转,旋转后的圆锥的体积是多少?
06
培优拓展
2.一个容积为2.5 L的酸奶瓶,瓶内酸奶高为20 cm。把酸奶瓶盖拧紧倒放,这时瓶中空的部分高为5 cm,请你算一算,瓶内酸奶的体积是多少?
正放或倒放时,酸奶和空的部分的体积和都是2.5 L;酸奶的体积不变,则两次空的部分体积也相等;正放时酸奶的体积加上倒放时空的部分的体积,和还是2.5 L。
20 cm
5
cm
2.5 L
20 cm
5cm
2.5 L
2.5 L
06
培优拓展
2500÷(20+5)×20=2000(cm3)
答:瓶内酸奶的体积是2 L。
2.5 L=2500 cm3
2000 cm3=2 L
2.一个容积为2.5 L的酸奶瓶,瓶内酸奶高为20 cm。把酸奶瓶盖拧紧倒放,这时瓶中空的部分高为5 cm,请你算一算,瓶内酸奶的体积是多少?
20 cm
5
cm
2.5 L
2.5 L
20 cm
5
cm
2.5 L
06
培优拓展
表面积 和 体积的本质不同,表面积是“外面包了多少”,体积是“里面能装多少”。
对于公式的梳理要一记二想三验算。复杂图形可拆解为基本图形再分步计算。
这节课你们都学会了哪些知识?
07
课堂小结
1.一个圆柱形水池,直径10米,深1米。
(2)在池底及池壁抹一层水泥,抹水泥部分的面积是多少?
(3)挖成这个水池,共需挖土多少立方米?
(1)这个水池占地面积是多少?
10÷2=5(米)3.14×5×5=78.5(平方米)
答:这个水池占地面积是78.5平方米。
2×3.14×5×1=31.4(平方米)78.5+31.4=109.9(平方米)
答:抹水泥部分的面积是109.9平方米。
3.14×5×5×1=78.5(立方米)
答:共需挖土78.5立方米。
08
作业布置
作业布置---知识技能类
2.一个棱长是10 cm的正方体,是由两个同样大小的长方体拼成的,原来一个长方体的表面积是( )cm2,体积是( )cm3。
10 cm
10 cm
10 cm
5 cm
10÷2=5(cm)
长方体的长:
表面积:
5×10×4+10×10×2
=200+200
=400(cm2)
体积:
5×10×10=500(cm3)
400
500
08
作业布置
作业布置---知识技能类
3.一个长方体的表面积是184 cm2,底面积是20 cm2,底面周长是18 cm,这个长方体的体积是( )cm3。
160
20 cm2
20 cm2
184-20×2=144(cm2)
144 cm2
cm
侧面积=表面积-底面积×2
144÷18=8(cm)
高=侧面积÷底面周长
20×8=160(cm3)
体积=底面积×高
18 cm
08
作业布置
作业布置---知识技能类
4.如下图,一个圆锥的高是3 cm,沿着它的高平均切成两部分,表面积就增加12 cm2,原来圆锥的底面直径是( )cm。
4
08
作业布置
作业布置---知识技能类
5.一个长方体罐头盒,长10cm、宽8cm、高6cm。在这个盒子的四周贴上商标纸,这张商标纸的面积是多少?长方体的罐头盒的体积是多少?
答:这张商标纸的面积是376cm2,长方体的罐头盒的体积是480cm3 。
(10×8+8×6+10×6)×2=376(cm2)
10×8×6=480(cm3)
08
作业布置
作业布置---知识技能类
整数和小数
09
板书设计
整数
负整数
0
自然数
小数
有限小数
无限小数
无限循环小数
数
无限不循环小数
正整数
https://www.21cnjy.com/recruitment/home/fine
(苏教版)六年级
下
图形与几何
立体图形的表面积和体积
01
教学目标
02
新知导入
03
任务一
04
任务二
05
拓展延伸
06
课堂练习
07
课堂小结
08
作业布置
09
板书设计
01
教学目标
1. 能准确区分表面积与体积(所占空间大小)的意义,并能举例说明生活中的应用场景。
2. 能熟练写出长方体、正方体、圆柱、圆锥等常见立体图形的表面积和体积公式,并解释公式中每个字母的含义。
3. 在计算中正确进行单位换算,并能分析结果是否符合实际。
立体图形的表面积和体积
长方体
正方体
表面积
体积
(长×宽+长×高+宽×高)×2
即S=2×(ab+ah+bh)
圆锥
01
复习导入
圆柱
表面积
体积
体积
表面积
体积
棱长×棱长×6 即S=6a
圆柱的侧面积+两个底面的面积
长 × 宽 × 高 V=abh
棱长×棱长×棱长 V=a
底面积×高 V=S底h=πr h
底面积×高÷3 V = Sh
02
任务一
学习任务一
知识梳理
a
h
b
下
右
左
前
后
上
长方体(或正方体)6个面的总面积,叫作它的表面积。
高
长
宽
高
长
宽
长方体的表面积:
(长×宽+长×高+宽×高)×2
即S=2×(ab+ah+bh)
长方体的表面积
02
知识梳理
正方体的表面积:
棱长×棱长×6
a
a
a
后
前
左
右
上
下
即S=6a
6个面的总面积
02
知识梳理
正方体的表面积
圆柱的表面积
圆柱的表面积=圆柱的侧面积+两个底面的面积
底面周长×高
侧面
底面
底面
底面周长=长方形的长。
长方形的宽
=圆柱的高。
S表=S侧 +2S底 =Ch+2πr2 =πdh+2πr =2πrh+2πr
02
知识梳理
体积和容积
立方厘米、立方分米、立方米。
升、毫升。
物体所占空间的大小叫作物体的体积。
容器所能容纳物体的体积叫作容器的容积。
计量容积,一般就用体积单位。计量液体的体积,通常用升或毫升作单位。
常用的体积单位:
常用的容积单位:
1粒花生米的
体积约1cm3
1盒牛奶大约有250毫升
02
知识梳理
体积单位间的进率:
1立方分米=1000立方厘米
升和毫升之间的进率是1000。
1升=1000毫升或1L=1000mL
升和毫升的进率:
1立方米=1000立方分米
每相邻单位之间的进率是1000。
1升=1立方分米
1毫升=1立方厘米
02
知识梳理
a
h
b
长方体的体积 = 长 × 宽 × 高
V=abh
长方体
正方体
正方体的体积
棱长
棱长
×
=
×
棱长
a
a
a
V=a
表示三个a相乘。
02
知识梳理
圆柱的体积
圆柱的底面积与长方体的底面积相等。
圆柱的高与长方体的高相等。
长方体的体积=底面积×高
圆柱的体积=长方体的体积
圆柱的体积=底面积×高
即V=S底h=πr h
02
知识梳理
圆柱和圆锥的体积
圆柱的体积
体积=底面积×高
圆心O
.
半径r
高 h
直径 d
侧面
.
体积=底面积×高÷3
.
半径r
高 h
侧面
底面
圆心O
.
圆锥的体积
圆锥的体积等于与它等底等高的圆柱体积的三分之一。
02
知识梳理
V=Sh
V= Sh
1
3
V=____
V=____
V=____
V=____
abh
a3
Sh
Sh
求物体的体积是从物体的外部来测量相关数据的,求物体的容积是从物体的内部来测量相关数据的。
V=____
Sh
02
知识梳理
在容器中装满水,把不规则物体完全浸入水中,溢出水的体积就是不规则物体的体积。
在粗细均匀的容器中倒入一定量的水,把不规则物体完全浸入水中,上升的水的体积就是不规则物体的体积。
利用体积不变的特征,把不规则物体转化成规则物体再进行计算。
溢出法
升高法
转化法
求不规则物体体积的方法
02
知识梳理
上升的水的体积就是鹅卵石的体积。
用“底面积×上升的高度”来计算。
怎样测量出一块拳头大的鹅卵石的体积?
02
知识梳理
03
任务二
学习任务二
典型例题
1.计算下面各图的表面积和体积。(图中单位:cm)
表面积:
(15×10+8×10+15×8)×2=700(cm2)
体积:
15×10×8=1200(cm3)
04
例题讲解
表面积:
6×10×10=600(cm2)
体积:
10×10×10=1000(cm3)
1.计算下面各图的表面积和体积。(图中单位:cm)
04
例题讲解
表面积:
2×3.14×42+3.14×8×12
=401.92(cm2)
体积:
3.14×42×12=602.88(cm3)
1.计算下面各图的表面积和体积。(图中单位:cm)
04
例题讲解
2.下面这个容器一共能装多少毫升水?(容器壁的厚度
忽略不计。)
8×5×2+3.14×(4÷2)2×3
=117.68(dm3)
=117680(mL)
答:这个容器能装117680毫升水。
04
例题讲解
3.一块圆锥形橡皮泥,底面积是12平方厘米,高是6厘米,
如果把它捏成同样高的一个圆柱,那么该圆柱的底面积
是多少平方厘米?
圆柱的底面积=体积÷高
24÷6=4(平方厘米)
答:该圆柱的底面积是4平方厘米。
04
例题讲解
圆锥体积=底面积×高×
1
3
12×6× =24(立方厘米)
1
3
4.一条水渠长800 m,横截面如下图。
(1)水渠的横截面积是多少平方米?
4×2.5=10(平方米)
答:水渠的横截面积是10平方米。
04
例题讲解
(2)水渠水深2 m,水在水渠中每分流动20 m,该水渠
每时的水流量是多少立方米?
2×4×20×60=9600(立方米)
答:该水渠每时的水流量是9600立方米。
04
例题讲解
1.求下面各圆柱的体积。
(1)底面积0.6平方米,高0.5平方米。
0.6×0.5=0.3(立方米)
(2)底面半径3厘米,高5厘米。
3.14×3 ×5=141.3(立方厘米)
(3)底面直径8米,高10米。
3.14×(8÷2) ×10=502.4(立方米)
----变式训练
05
课堂练习
2. 一台长方体形冰箱长0.6 m,宽0.5 m,高1.8 m。
(1)做这台冰箱的包装盒至少需要纸板多少平方米?
(2)这台冰箱占地面积是多少平方米?
(1)(0.6×0.5+0.6×1.8+0.5×1.8)×2=4.56(m2)
答:做这台冰箱的包装盒至少需要纸板4.56平方米。
(2)0.6×0.5=0.3(m2)
答:这台冰箱占地面积是0.3平方米。
----变式训练
05
课堂练习
3.一种空心的混凝土管道,内直径是40厘米,外直径是80厘米,长300厘米,求制作100节这种管道约需多少混凝土?
内半径是:40÷2=20(厘米)=0.2米
外半径是:80÷2=40(厘米)=0.4米
300厘米=3米
环形圆柱的体积:3.14×(0.4 -0.2 )×3=1.1304(立方米)
制作100节这种管道需要混凝土:
1.1304×100=113.04(立方米)
答:制作100节这种管道需要113.04立方米混凝土。
----变式训练
05
课堂练习
4.一种抽水机出水管的直径是1分米,管口水流的速度是每秒2米,1分钟能抽多少立方米?
1分米=0.1米
3.14×(0.1÷2) ×2=0.0157(立方米)
0.0157×60=0.942(立方米)
答:1分钟能抽0.942立方米。
----变式训练
05
课堂练习
5.用一根长24 cm的铁丝围一个长方体(或正方体)框架。在这个长方体的表面糊一层纸,怎样围框架用纸最多?
由题意可知,铁丝的长度就是长方体(或正方体)的棱长总和。长方体有4组长、宽、高,
24÷4=6(cm),
可以得出一组长、宽、高的和是6 cm。
求怎样围框架用纸最多,就是要使长方体(或正方体)的表面积最大。
----变式训练
05
课堂练习
06
任务四
学习任务四
培优拓展
1.将一个直角边分别为7厘米、9厘米的直角三角形,以一条直角边所在的直线为轴旋转,旋转后的圆锥的体积是多少?
7 cm
9 cm
13
3.14×92×7×-=593.46(cm3)
06
培优拓展
7 cm
9 cm
13
3.14×72×9×-=461.58(cm3)
593.46>461.58
答:以7厘米的直角边所在的直线为轴旋转,得到的圆锥的体积最大。
1.将一个直角边分别为7厘米、9厘米的直角三角形,以一条直角边所在的直线为轴旋转,旋转后的圆锥的体积是多少?
06
培优拓展
2.一个容积为2.5 L的酸奶瓶,瓶内酸奶高为20 cm。把酸奶瓶盖拧紧倒放,这时瓶中空的部分高为5 cm,请你算一算,瓶内酸奶的体积是多少?
正放或倒放时,酸奶和空的部分的体积和都是2.5 L;酸奶的体积不变,则两次空的部分体积也相等;正放时酸奶的体积加上倒放时空的部分的体积,和还是2.5 L。
20 cm
5
cm
2.5 L
20 cm
5cm
2.5 L
2.5 L
06
培优拓展
2500÷(20+5)×20=2000(cm3)
答:瓶内酸奶的体积是2 L。
2.5 L=2500 cm3
2000 cm3=2 L
2.一个容积为2.5 L的酸奶瓶,瓶内酸奶高为20 cm。把酸奶瓶盖拧紧倒放,这时瓶中空的部分高为5 cm,请你算一算,瓶内酸奶的体积是多少?
20 cm
5
cm
2.5 L
2.5 L
20 cm
5
cm
2.5 L
06
培优拓展
表面积 和 体积的本质不同,表面积是“外面包了多少”,体积是“里面能装多少”。
对于公式的梳理要一记二想三验算。复杂图形可拆解为基本图形再分步计算。
这节课你们都学会了哪些知识?
07
课堂小结
1.一个圆柱形水池,直径10米,深1米。
(2)在池底及池壁抹一层水泥,抹水泥部分的面积是多少?
(3)挖成这个水池,共需挖土多少立方米?
(1)这个水池占地面积是多少?
10÷2=5(米)3.14×5×5=78.5(平方米)
答:这个水池占地面积是78.5平方米。
2×3.14×5×1=31.4(平方米)78.5+31.4=109.9(平方米)
答:抹水泥部分的面积是109.9平方米。
3.14×5×5×1=78.5(立方米)
答:共需挖土78.5立方米。
08
作业布置
作业布置---知识技能类
2.一个棱长是10 cm的正方体,是由两个同样大小的长方体拼成的,原来一个长方体的表面积是( )cm2,体积是( )cm3。
10 cm
10 cm
10 cm
5 cm
10÷2=5(cm)
长方体的长:
表面积:
5×10×4+10×10×2
=200+200
=400(cm2)
体积:
5×10×10=500(cm3)
400
500
08
作业布置
作业布置---知识技能类
3.一个长方体的表面积是184 cm2,底面积是20 cm2,底面周长是18 cm,这个长方体的体积是( )cm3。
160
20 cm2
20 cm2
184-20×2=144(cm2)
144 cm2
cm
侧面积=表面积-底面积×2
144÷18=8(cm)
高=侧面积÷底面周长
20×8=160(cm3)
体积=底面积×高
18 cm
08
作业布置
作业布置---知识技能类
4.如下图,一个圆锥的高是3 cm,沿着它的高平均切成两部分,表面积就增加12 cm2,原来圆锥的底面直径是( )cm。
4
08
作业布置
作业布置---知识技能类
5.一个长方体罐头盒,长10cm、宽8cm、高6cm。在这个盒子的四周贴上商标纸,这张商标纸的面积是多少?长方体的罐头盒的体积是多少?
答:这张商标纸的面积是376cm2,长方体的罐头盒的体积是480cm3 。
(10×8+8×6+10×6)×2=376(cm2)
10×8×6=480(cm3)
08
作业布置
作业布置---知识技能类
整数和小数
09
板书设计
整数
负整数
0
自然数
小数
有限小数
无限小数
无限循环小数
数
无限不循环小数
正整数
https://www.21cnjy.com/recruitment/home/fine
同课章节目录
