初中数学苏科版(2024)七年级下册 12.4 定理2 课件(15张PPT )
文档属性
| 名称 | 初中数学苏科版(2024)七年级下册 12.4 定理2 课件(15张PPT ) |

|
|
| 格式 | pptx | ||
| 文件大小 | 1.9MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 苏科版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2025-05-29 11:04:24 | ||
图片预览





文档简介
(共15张PPT)
定理2
学习目标
探索并掌握多边形的内角和定理,外角和定理,并能简单应用
理解多边形内角和、外角和定理之间的关系,进一步感悟定理的运用
温故旧知
1.三角形内角和定理:三角形内角和是 。
2.三角形内角和定理的推论是 。
180°
三角形的外角等于与它不相邻的两个
内角的和.
温故知新
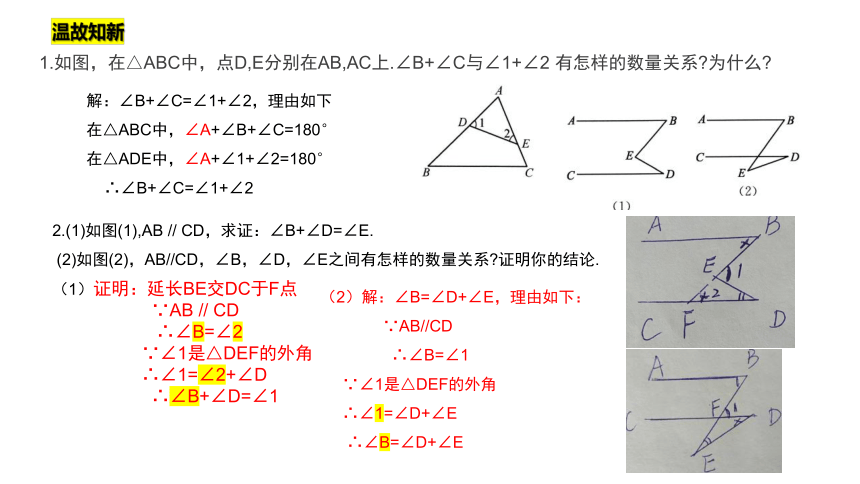
1.如图,在△ABC中,点D,E分别在AB,AC上.∠B+∠C与∠1+∠2 有怎样的数量关系 为什么
解:∠B+∠C=∠1+∠2,理由如下
在△ABC中,∠A+∠B+∠C=180°
在△ADE中,∠A+∠1+∠2=180°
∴∠B+∠C=∠1+∠2
2.(1)如图(1),AB // CD,求证:∠B+∠D=∠E.
(2)如图(2),AB//CD,∠B,∠D,∠E之间有怎样的数量关系 证明你的结论.
(1)证明:延长BE交DC于F点
∵AB // CD
∴∠B=∠2
∵∠1是△DEF的外角
∴∠1=∠2+∠D
∴∠B+∠D=∠1
(2)解:∠B=∠D+∠E,理由如下:
∵AB//CD
∴∠B=∠1
∵∠1是△DEF的外角
∴∠1=∠D+∠E
∴∠B=∠D+∠E
探索活动
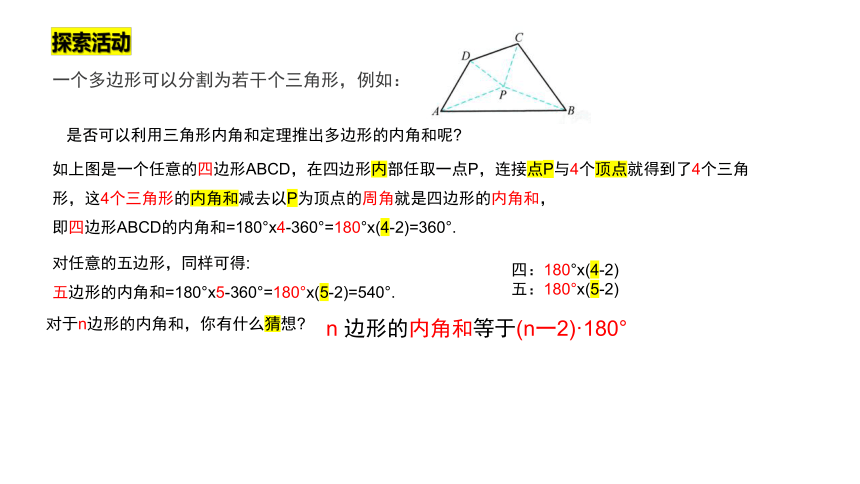
一个多边形可以分割为若干个三角形,例如:
是否可以利用三角形内角和定理推出多边形的内角和呢
如上图是一个任意的四边形ABCD,在四边形内部任取一点P,连接点P与4个顶点就得到了4个三角形,这4个三角形的内角和减去以P为顶点的周角就是四边形的内角和,
即四边形ABCD的内角和=180°x4-360°=180°x(4-2)=360°.
对任意的五边形,同样可得:
五边形的内角和=180°x5-360°=180°x(5-2)=540°.
对于n边形的内角和,你有什么猜想
四:180°x(4-2)
五:180°x(5-2)
n 边形的内角和等于(n一2)·180°
新知学习
一.多边形的内角和定理:
n 边形的内角和等于(n一2)·180°
1.十边形的内角和是 .
2. 边形的内角和的900°
(10-2)×180°=1440°
1440°
∵(n一2)·180°=900°
∴ n一2=5
∴ n=7
七
例题学习
1.已知:如图,∠ABC+∠C+∠CDE=360°,GH分别交AB,ED 于点G,H.
求证:∠1=∠2.
证明:∵五边形HDCBG内角和为
(5-2)×180°=540°
又∵∠ABC+∠C+∠CDE=360° (已知)
∴∠BGH+∠GHD=180° (等式的性质)
∵ ∠GHD=∠2 (对顶角相等)
∴ ∠BGH+∠2=180° (等量代换)
∵ ∠BGH+∠1=180° (平角的定义)
∴ ∠1=∠2. ( 等量代换)
活动探索
内角和有一般规律,外角和也有一般规律吗 仿照多边形的内角和研究过程,如何求多边形的外角和
如图△ABC的3个内角及3个对应外角共形成3个平角,因为三角形的内角和为180°,
所以三角形的外角和是:180°X3-180°=360°
.
如图,四边形ABCD的4个内角及4个对应外角共形成4个平角,因为四边形的内角和为360°,
所以四边形的外角和=180°X4-360°=360°.
我们可以把上面的结果推广到一般的n边形,得到:
多边形的外角和=180°Xn-多边形的内角和
= 180°Xn-180°X(n-2)
= 180°x2=360°.
新知学习
二.多边形外角和定理:多边形的外角和等于360°.
1.十边形的外角和是 。
2.一个多边形的内角和与外角和相等,这个多边形 是边形
3.如图,在操场上画出一个任意的多边形,然后从边AB上的一点S出发,沿着A→B方向,到达点B后再转向B→C方向,这样走完一圈回到点S后,一共转过了 度。
360°
由:(n一2)·180°=360°
n一2=2
n=4
4
360°
例题学习
2.如图,在四边形ABCD中,∠A+∠C=180°,∠ABE是四边形ABCD的一个外角,∠ABE与∠D相等吗 证明你的结论.
解:∠ABE=∠D,理由如下;
∵四边形ABCD的内角和=(4-2)×180°=360°
又∵∠A+∠C=180°
∴∠ABC+∠D =180°
∵∠ABC+∠ABE =180°
∴ ∠ABE=∠D
练习巩固
1.在五边形 ABCDE 中,∠A=∠E=120°,∠B=130∠C=70°,则∠D的大小为( )
A.100° B.110° C.120° D.130°
2.若一个正多边形的内角和是其外角和的2倍,则这个正多边形的每个内角为________
3.如图,∠1,∠2,∠3 是五边形 ABCDE的三个外角,边AE,CD的延长线相交于点F,如果∠F=a,
那么∠1+∠2+∠3的大小为 ( )
A.270°-a B.360°-a C.90°+a D.180°+a
A
2.由 (n一2)·180°=2×360°
n一2=4
n=6
∵是正多边形,∴每个内角都相等
∴每个内角度数= (6一2)·180°÷6=120°
120°
3.∵五边形ABCDE的外角和=360°
∴∠1+∠2+∠3+∠FED+∠FDE=360°
又∵∠F+∠FED+∠FDE=180°
∴360°-(∠1+∠2+∠3)=180°-∠F
∴ ∠1+∠2+∠3= 180+∠F
∴ ∠1+∠2+∠3=a+180°
D
课堂检测
1..已知一个多边形的内角和比外角和多900°,并且这个多边形各个内角的度数都相等。
这个多边形的每个内角是多少度
2.如图,在四边形ABCD中,AD//BC,连接 BD,点E在选BC上,点F在边DC上,且∠1=∠2,
(1)求证:EF//BD:
(2)若BD平分∠ABC,∠A=130,∠C=70°,求∠CFE的度数
1.解:由(n一2)·180°=360°+900°得
n=9
∵每个内角都相等
∴每个内角度数=(360°+900°)÷9=140°
答:这个多边形的每个内角是140°
2.(1)证明:∵AD//BC
∴∠1=∠DBC
∵ ∠1=∠2
∴ ∠2=∠DBC
∴EF//BD:
2.(2)∵AD//BC,∠A=130
∴∠ABC=180°-∠A=130°
∵BD平分∠ABC
∴∠DBC=∠ABC=65°
由(1)得:∠2=∠DBC=65°
∵∠C=70° ∴∠CFE=180-∠C-∠2=45°
素养提升
如图①,求证:∠BOC=∠A+∠B+∠C.
[直观应用]
(1)根据上述结论,若图②中,∠EDF=α,则∠A,∠B,∠C,∠D,∠E,∠F的度数之和等于 (直接给出结论,不必说明理由)。
(2)根据上述结论,求图③中∠A,∠B,∠C,∠D.∠E的数之和,并证明你的结论.
[类比联系](3)如图①.求∠A,∠B,/C,∠D,∠E,∠F,∠G的度数之和,并证明你的结论.
总结反思
一.多边形的内角和定理:
n 边形的内角和=(n一2)·180°
二.多边形外角和定理:多边形的外角和=360°.
谢谢观看!
定理2
学习目标
探索并掌握多边形的内角和定理,外角和定理,并能简单应用
理解多边形内角和、外角和定理之间的关系,进一步感悟定理的运用
温故旧知
1.三角形内角和定理:三角形内角和是 。
2.三角形内角和定理的推论是 。
180°
三角形的外角等于与它不相邻的两个
内角的和.
温故知新
1.如图,在△ABC中,点D,E分别在AB,AC上.∠B+∠C与∠1+∠2 有怎样的数量关系 为什么
解:∠B+∠C=∠1+∠2,理由如下
在△ABC中,∠A+∠B+∠C=180°
在△ADE中,∠A+∠1+∠2=180°
∴∠B+∠C=∠1+∠2
2.(1)如图(1),AB // CD,求证:∠B+∠D=∠E.
(2)如图(2),AB//CD,∠B,∠D,∠E之间有怎样的数量关系 证明你的结论.
(1)证明:延长BE交DC于F点
∵AB // CD
∴∠B=∠2
∵∠1是△DEF的外角
∴∠1=∠2+∠D
∴∠B+∠D=∠1
(2)解:∠B=∠D+∠E,理由如下:
∵AB//CD
∴∠B=∠1
∵∠1是△DEF的外角
∴∠1=∠D+∠E
∴∠B=∠D+∠E
探索活动
一个多边形可以分割为若干个三角形,例如:
是否可以利用三角形内角和定理推出多边形的内角和呢
如上图是一个任意的四边形ABCD,在四边形内部任取一点P,连接点P与4个顶点就得到了4个三角形,这4个三角形的内角和减去以P为顶点的周角就是四边形的内角和,
即四边形ABCD的内角和=180°x4-360°=180°x(4-2)=360°.
对任意的五边形,同样可得:
五边形的内角和=180°x5-360°=180°x(5-2)=540°.
对于n边形的内角和,你有什么猜想
四:180°x(4-2)
五:180°x(5-2)
n 边形的内角和等于(n一2)·180°
新知学习
一.多边形的内角和定理:
n 边形的内角和等于(n一2)·180°
1.十边形的内角和是 .
2. 边形的内角和的900°
(10-2)×180°=1440°
1440°
∵(n一2)·180°=900°
∴ n一2=5
∴ n=7
七
例题学习
1.已知:如图,∠ABC+∠C+∠CDE=360°,GH分别交AB,ED 于点G,H.
求证:∠1=∠2.
证明:∵五边形HDCBG内角和为
(5-2)×180°=540°
又∵∠ABC+∠C+∠CDE=360° (已知)
∴∠BGH+∠GHD=180° (等式的性质)
∵ ∠GHD=∠2 (对顶角相等)
∴ ∠BGH+∠2=180° (等量代换)
∵ ∠BGH+∠1=180° (平角的定义)
∴ ∠1=∠2. ( 等量代换)
活动探索
内角和有一般规律,外角和也有一般规律吗 仿照多边形的内角和研究过程,如何求多边形的外角和
如图△ABC的3个内角及3个对应外角共形成3个平角,因为三角形的内角和为180°,
所以三角形的外角和是:180°X3-180°=360°
.
如图,四边形ABCD的4个内角及4个对应外角共形成4个平角,因为四边形的内角和为360°,
所以四边形的外角和=180°X4-360°=360°.
我们可以把上面的结果推广到一般的n边形,得到:
多边形的外角和=180°Xn-多边形的内角和
= 180°Xn-180°X(n-2)
= 180°x2=360°.
新知学习
二.多边形外角和定理:多边形的外角和等于360°.
1.十边形的外角和是 。
2.一个多边形的内角和与外角和相等,这个多边形 是边形
3.如图,在操场上画出一个任意的多边形,然后从边AB上的一点S出发,沿着A→B方向,到达点B后再转向B→C方向,这样走完一圈回到点S后,一共转过了 度。
360°
由:(n一2)·180°=360°
n一2=2
n=4
4
360°
例题学习
2.如图,在四边形ABCD中,∠A+∠C=180°,∠ABE是四边形ABCD的一个外角,∠ABE与∠D相等吗 证明你的结论.
解:∠ABE=∠D,理由如下;
∵四边形ABCD的内角和=(4-2)×180°=360°
又∵∠A+∠C=180°
∴∠ABC+∠D =180°
∵∠ABC+∠ABE =180°
∴ ∠ABE=∠D
练习巩固
1.在五边形 ABCDE 中,∠A=∠E=120°,∠B=130∠C=70°,则∠D的大小为( )
A.100° B.110° C.120° D.130°
2.若一个正多边形的内角和是其外角和的2倍,则这个正多边形的每个内角为________
3.如图,∠1,∠2,∠3 是五边形 ABCDE的三个外角,边AE,CD的延长线相交于点F,如果∠F=a,
那么∠1+∠2+∠3的大小为 ( )
A.270°-a B.360°-a C.90°+a D.180°+a
A
2.由 (n一2)·180°=2×360°
n一2=4
n=6
∵是正多边形,∴每个内角都相等
∴每个内角度数= (6一2)·180°÷6=120°
120°
3.∵五边形ABCDE的外角和=360°
∴∠1+∠2+∠3+∠FED+∠FDE=360°
又∵∠F+∠FED+∠FDE=180°
∴360°-(∠1+∠2+∠3)=180°-∠F
∴ ∠1+∠2+∠3= 180+∠F
∴ ∠1+∠2+∠3=a+180°
D
课堂检测
1..已知一个多边形的内角和比外角和多900°,并且这个多边形各个内角的度数都相等。
这个多边形的每个内角是多少度
2.如图,在四边形ABCD中,AD//BC,连接 BD,点E在选BC上,点F在边DC上,且∠1=∠2,
(1)求证:EF//BD:
(2)若BD平分∠ABC,∠A=130,∠C=70°,求∠CFE的度数
1.解:由(n一2)·180°=360°+900°得
n=9
∵每个内角都相等
∴每个内角度数=(360°+900°)÷9=140°
答:这个多边形的每个内角是140°
2.(1)证明:∵AD//BC
∴∠1=∠DBC
∵ ∠1=∠2
∴ ∠2=∠DBC
∴EF//BD:
2.(2)∵AD//BC,∠A=130
∴∠ABC=180°-∠A=130°
∵BD平分∠ABC
∴∠DBC=∠ABC=65°
由(1)得:∠2=∠DBC=65°
∵∠C=70° ∴∠CFE=180-∠C-∠2=45°
素养提升
如图①,求证:∠BOC=∠A+∠B+∠C.
[直观应用]
(1)根据上述结论,若图②中,∠EDF=α,则∠A,∠B,∠C,∠D,∠E,∠F的度数之和等于 (直接给出结论,不必说明理由)。
(2)根据上述结论,求图③中∠A,∠B,∠C,∠D.∠E的数之和,并证明你的结论.
[类比联系](3)如图①.求∠A,∠B,/C,∠D,∠E,∠F,∠G的度数之和,并证明你的结论.
总结反思
一.多边形的内角和定理:
n 边形的内角和=(n一2)·180°
二.多边形外角和定理:多边形的外角和=360°.
谢谢观看!
同课章节目录
- 第7章 平面图形的认识(二)
- 7.1 探索直线平行的条件
- 7.2 探索平行线的性质
- 7.3 图形的平移
- 7.4 认识三角形
- 7.5 多边形的内角和与外角和
- 第8章 幂的运算
- 8.1 同底数幂的乘法
- 8.2 幂的乘方与积的乘方
- 8.3 同底数幂的除法
- 第9章 整式乘法与因式分解
- 9.1 单项式乘单项式
- 9.2 单项式乘多项式
- 9.3 多项式乘多项式
- 9.4 乘法公式
- 9.5 多项式的因式分解
- 第10章 二元一次方程组
- 10.1 二元一次方程
- 10.2 二元一次方程组
- 10.3 解二元一次方程组
- 10.4 三元一次方程组
- 10.5 用二元一次方程解决问题
- 第11章 一元一次不等式
- 11.1 生活中的不等式
- 11.2 不等式的解集
- 11.3 不等式的性质
- 11.4 解一元一次不等式
- 11.5 用一元一次不等式解决问题
- 11.6 一元一次不等式组
- 第12章 证明
- 12.1 定义与命题
- 12.2 证明
- 12.3 互逆命题
