第八章 实数 复习教案(含答案)七年级下册数学人教版(2024)期末四步复习法
文档属性
| 名称 | 第八章 实数 复习教案(含答案)七年级下册数学人教版(2024)期末四步复习法 | 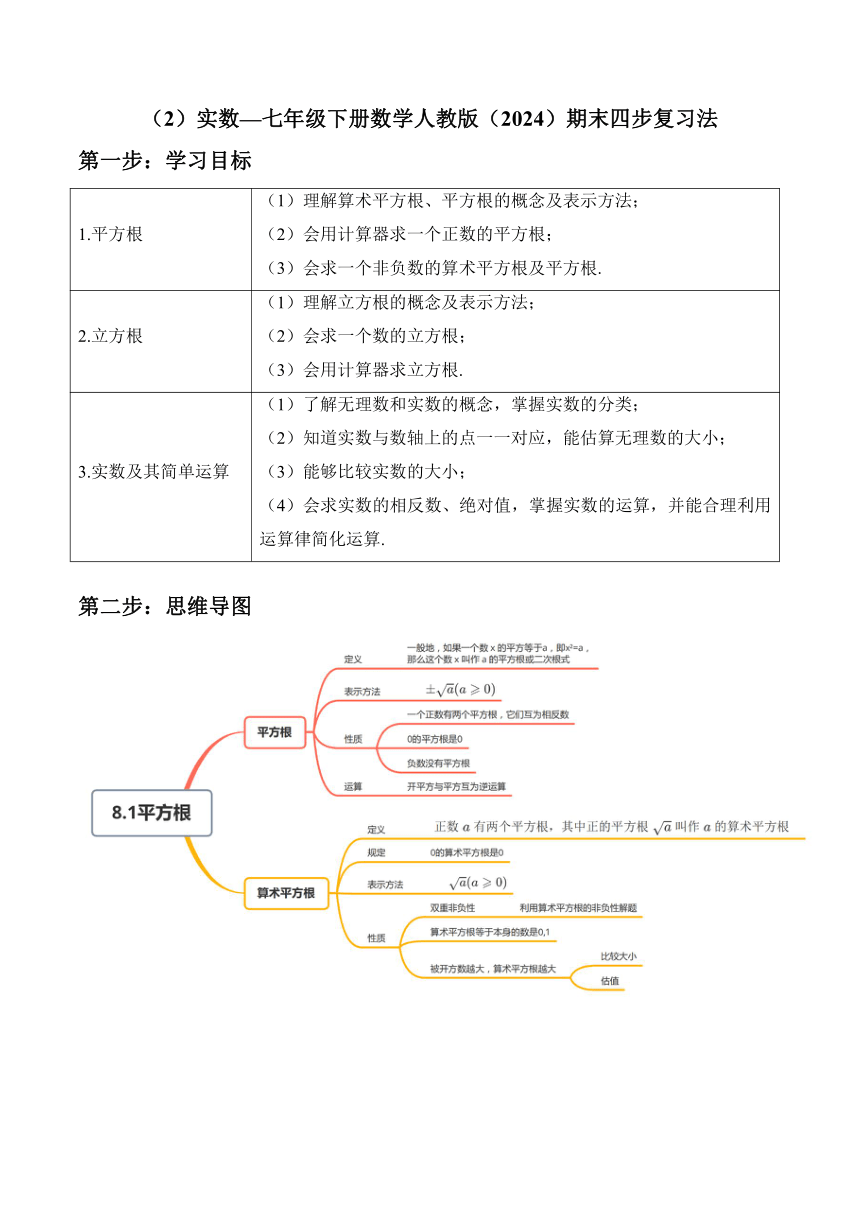 | |
| 格式 | docx | ||
| 文件大小 | 812.1KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 通用版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2025-05-29 11:12:32 | ||
图片预览




文档简介
(2)实数—七年级下册数学人教版(2024)期末四步复习法
第一步:学习目标
1.平方根 (1)理解算术平方根、平方根的概念及表示方法; (2)会用计算器求一个正数的平方根; (3)会求一个非负数的算术平方根及平方根.
2.立方根 (1)理解立方根的概念及表示方法; (2)会求一个数的立方根; (3)会用计算器求立方根.
3.实数及其简单运算 (1)了解无理数和实数的概念,掌握实数的分类; (2)知道实数与数轴上的点一一对应,能估算无理数的大小; (3)能够比较实数的大小; (4)会求实数的相反数、绝对值,掌握实数的运算,并能合理利用运算律简化运算.
第二步:思维导图
第三步:重难知识、易混易错
平方根:一般地,如果一个数的平方等于a,那么这个数叫做a的平方根,也叫做a的二次方根.
正数的平方根有两个,它们互为相反数,其中正的平方根就是这个数的算术平方根;0只有一个平方根,是0;负数没有平方根.
开平方:求一个数a的平方根的运算,叫做开平方.(a叫做被开方数)平方与开平方互逆运算.
【例题】已知,则x的值为_________.
答案:3或-1
解析:∵,
∴,
∴或,
∴或,
故答案为:3或.
【例题】若一个正数的平方根是和,则这个正数是( )
A.30 B.25 C. D.50
答案:B
解析:∵一个正数的平方根是和,
∴,
∴,
∴,
∴这个正数是,
故选:B.
算术平方根:一般地,如果一个正数x的平方等于a,即,那么这个正数x叫做a的算术平方根.非负数a的算术平方根记为,读作“根号a”,a叫做被开方数.
规定:0的算术平方根是0
【注意】算术平方根是它本身的数只有1和0.
【例题】的算术平方根是______.
答案:3
解析:,9的算术平方根为3
的算术平方根为3.
故答案为:3.
【例题】已知,,则______.
答案:6250
解析:∵,
∴,
故答案为:6250.
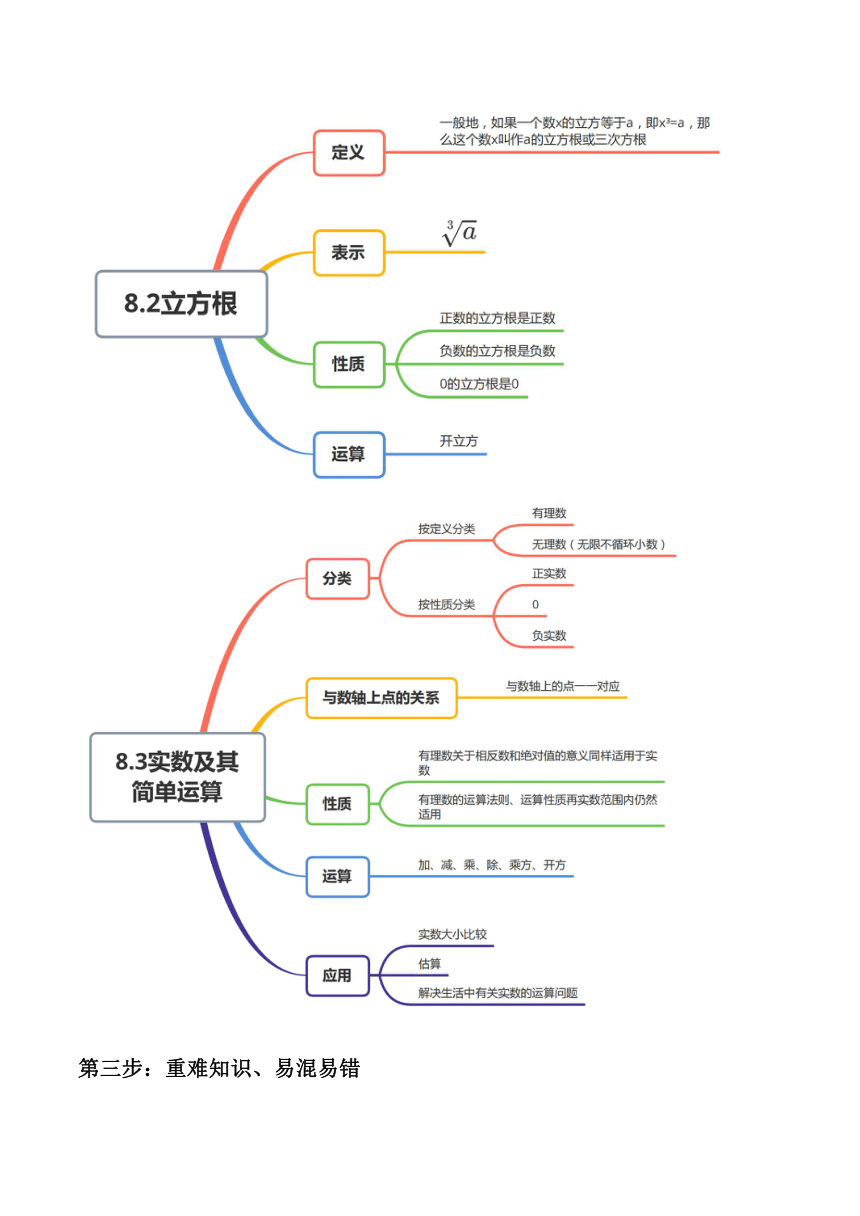
立方根:一般地,如果一个数的立方等于a,这个数就叫做a的立方根,也叫做a的三次方根.
一个数a的立方根,用符号“ ”表示,读作“ 三次根号a”,其中a是被开方数,3是根指数.
一个正数有一个正的立方根;一个负数有一个负的立方根,零的立方根是零.
任何有理数都有立方根,而且它的立方根是唯一的.
开立方:求一个数的立方根的运算,叫作开立方.
根据开立方与立方的互逆运算关系,我们可以借助立方运算求一个数的立方根.
【注意】(1)中的根指数3不能省略,而算术平方根的根指数2可以省略;
(2)互为相反数的两个数,它们的立方根也互为相反数.
【例题】若,则x的值是( )
A. B. C. D.
答案:A
解析:,
∴,
解得:.
故选:A
【例题】的立方根是__________.
答案:
解析:,的立方根是,故答案为.
无理数:无限不循环小数又叫做无理数.
实数的分类:按定义分:
按大小分:
【例题】下列各数中:,,,,,,(相邻两个2之间0的个数依次加1),无理数有( )
A.2个 B.3个 C.4个 D.5个
答案:B
解析:是有理数,是无理数,是分数属于有理数,是无理数,是有理数,是有理数,(相邻两个2之间0的个数依次加1)是无理数.
综上,无理数有3个.
故选B.
【例题】下列实数中,有理数是( )
A. B. C. D.
答案:B
解析:,
是有理数,而、、是无理数;
故选B.
实数与数轴:实数与数轴上的点是一一对应的,即每一个实数都可以用数轴上的一个点来表示;反过来,数轴上的每一个点都表示一个实数.与规定有理数的大小一样,对于数轴上的任意两个点,右边的点表示实数总比左边的点表示的实数大.
【例题】如图,数轴上有M,N,P,Q四个点,则下列说法正确的是( )
A.点M表示的数可能是 B.点N表示的数可能是
C.点P表示的数可能是 D.点Q表示的数可能是
答案:C
解析:A.,点A表示的数小于1,故选项说法错误,不符合题意;
B. ,点B表示的数在1.5和2之间,故选项说法错误,不符合题意;
C.,点C表示的数在和2.5之间,故选项说法正确,符合题意;
D.,点D表示的数大于4,故选项说法错误,不符合题意.
故选:C.
实数的大小比较:(1)数轴上的两个点表示的数,右边的数总比左边的数大;
(2)负实数 < 0 < 正实数
(3)两个正实数,绝对值大的较大;两个负实数,绝对值大的反而较小
【例题】比较大小:______(填“>”或“<”).
答案:>
解析:∵
∴.
故答案为:>.
【例题】比较大小:____________5.(填“>”“=”或“<”)
答案:<
解析:,,
,
.
故答案为:<.
相反数:数a的相反数是-a,这里a表示任意一个实数.
绝对值:一个正实数的绝对值是它本身,一个负实数的绝对值是它的相反数;0的绝对值是0.
即:
实数的运算:先乘方、开方,在乘除,最后加减;如有括号,先进行括号内的运算,一般按小括号、中号、大括号依次进行;同级运算,从左到右进行.
【例题】计算:.
答案:4
解析:原式.
【例题】的相反数为_________.
答案:
解析:由题意知,的相反数为,
故答案为:.
【例题】计算:.
答案:
解析:原式
.
第四步:对接中考
1.[2024年广东中考真题]完全相同的4个正方形面积之和是100,则正方形的边长是( )
A.2 B.5 C.10 D.20
2.[2024年新疆中考真题]估计的值在( )
A.2和3之间 B.3和4之间 C.4和5之间 D.5和6之间
3.[2024年天津中考真题]估计的值在( )
A.1和2之间 B.2和3之间 C.3和4之间 D.4和5之间
4.[2024年福建中考真题]下列实数中,无理数是( )
A. B.0 C. D.
5.[2024年宁夏中考真题]下列各数中,无理数是( )
A.-1 B. C. D.π
6.[2024年四川巴中中考真题]在0,1,,中最小的实数是( )
A.0 B. C.1 D.
7.[2024年青海中考真题]-8的立方根是________.
8.[2024年四川巴中中考真题]27的立方根为__________.
9.[2024年山西中考真题]比较大小:________2(填“>”“<”或“=”).
答案以及解析
对接中考
1.答案:B
解析:根据题意得:,
则正方形的边长为5,
故选: B.
2.答案:A
解析:,,估计的值在2和3之间.
3.答案:C
解析:,
,
即在3和4之间,
故选:C.
4.答案:D
解析:-3,0是整数,是分数,它们不是无理数;5是无限不循环小数,它是无理数,
故选D.
5.答案:D
解析:,是整数,是分数,它们不是无理数;
是无限不循环小数,它是无理数;
故选:D.
6.答案:B
解析:,
最小的实数是,
故选:B.
7.答案:-2
解析:,
的立方根是.
答案:-2.
8.答案:3
解析:,
的立方根是3,
故答案为:3.
9.答案:>
解析:,,
,
,
故答案为:>.
第一步:学习目标
1.平方根 (1)理解算术平方根、平方根的概念及表示方法; (2)会用计算器求一个正数的平方根; (3)会求一个非负数的算术平方根及平方根.
2.立方根 (1)理解立方根的概念及表示方法; (2)会求一个数的立方根; (3)会用计算器求立方根.
3.实数及其简单运算 (1)了解无理数和实数的概念,掌握实数的分类; (2)知道实数与数轴上的点一一对应,能估算无理数的大小; (3)能够比较实数的大小; (4)会求实数的相反数、绝对值,掌握实数的运算,并能合理利用运算律简化运算.
第二步:思维导图
第三步:重难知识、易混易错
平方根:一般地,如果一个数的平方等于a,那么这个数叫做a的平方根,也叫做a的二次方根.
正数的平方根有两个,它们互为相反数,其中正的平方根就是这个数的算术平方根;0只有一个平方根,是0;负数没有平方根.
开平方:求一个数a的平方根的运算,叫做开平方.(a叫做被开方数)平方与开平方互逆运算.
【例题】已知,则x的值为_________.
答案:3或-1
解析:∵,
∴,
∴或,
∴或,
故答案为:3或.
【例题】若一个正数的平方根是和,则这个正数是( )
A.30 B.25 C. D.50
答案:B
解析:∵一个正数的平方根是和,
∴,
∴,
∴,
∴这个正数是,
故选:B.
算术平方根:一般地,如果一个正数x的平方等于a,即,那么这个正数x叫做a的算术平方根.非负数a的算术平方根记为,读作“根号a”,a叫做被开方数.
规定:0的算术平方根是0
【注意】算术平方根是它本身的数只有1和0.
【例题】的算术平方根是______.
答案:3
解析:,9的算术平方根为3
的算术平方根为3.
故答案为:3.
【例题】已知,,则______.
答案:6250
解析:∵,
∴,
故答案为:6250.
立方根:一般地,如果一个数的立方等于a,这个数就叫做a的立方根,也叫做a的三次方根.
一个数a的立方根,用符号“ ”表示,读作“ 三次根号a”,其中a是被开方数,3是根指数.
一个正数有一个正的立方根;一个负数有一个负的立方根,零的立方根是零.
任何有理数都有立方根,而且它的立方根是唯一的.
开立方:求一个数的立方根的运算,叫作开立方.
根据开立方与立方的互逆运算关系,我们可以借助立方运算求一个数的立方根.
【注意】(1)中的根指数3不能省略,而算术平方根的根指数2可以省略;
(2)互为相反数的两个数,它们的立方根也互为相反数.
【例题】若,则x的值是( )
A. B. C. D.
答案:A
解析:,
∴,
解得:.
故选:A
【例题】的立方根是__________.
答案:
解析:,的立方根是,故答案为.
无理数:无限不循环小数又叫做无理数.
实数的分类:按定义分:
按大小分:
【例题】下列各数中:,,,,,,(相邻两个2之间0的个数依次加1),无理数有( )
A.2个 B.3个 C.4个 D.5个
答案:B
解析:是有理数,是无理数,是分数属于有理数,是无理数,是有理数,是有理数,(相邻两个2之间0的个数依次加1)是无理数.
综上,无理数有3个.
故选B.
【例题】下列实数中,有理数是( )
A. B. C. D.
答案:B
解析:,
是有理数,而、、是无理数;
故选B.
实数与数轴:实数与数轴上的点是一一对应的,即每一个实数都可以用数轴上的一个点来表示;反过来,数轴上的每一个点都表示一个实数.与规定有理数的大小一样,对于数轴上的任意两个点,右边的点表示实数总比左边的点表示的实数大.
【例题】如图,数轴上有M,N,P,Q四个点,则下列说法正确的是( )
A.点M表示的数可能是 B.点N表示的数可能是
C.点P表示的数可能是 D.点Q表示的数可能是
答案:C
解析:A.,点A表示的数小于1,故选项说法错误,不符合题意;
B. ,点B表示的数在1.5和2之间,故选项说法错误,不符合题意;
C.,点C表示的数在和2.5之间,故选项说法正确,符合题意;
D.,点D表示的数大于4,故选项说法错误,不符合题意.
故选:C.
实数的大小比较:(1)数轴上的两个点表示的数,右边的数总比左边的数大;
(2)负实数 < 0 < 正实数
(3)两个正实数,绝对值大的较大;两个负实数,绝对值大的反而较小
【例题】比较大小:______(填“>”或“<”).
答案:>
解析:∵
∴.
故答案为:>.
【例题】比较大小:____________5.(填“>”“=”或“<”)
答案:<
解析:,,
,
.
故答案为:<.
相反数:数a的相反数是-a,这里a表示任意一个实数.
绝对值:一个正实数的绝对值是它本身,一个负实数的绝对值是它的相反数;0的绝对值是0.
即:
实数的运算:先乘方、开方,在乘除,最后加减;如有括号,先进行括号内的运算,一般按小括号、中号、大括号依次进行;同级运算,从左到右进行.
【例题】计算:.
答案:4
解析:原式.
【例题】的相反数为_________.
答案:
解析:由题意知,的相反数为,
故答案为:.
【例题】计算:.
答案:
解析:原式
.
第四步:对接中考
1.[2024年广东中考真题]完全相同的4个正方形面积之和是100,则正方形的边长是( )
A.2 B.5 C.10 D.20
2.[2024年新疆中考真题]估计的值在( )
A.2和3之间 B.3和4之间 C.4和5之间 D.5和6之间
3.[2024年天津中考真题]估计的值在( )
A.1和2之间 B.2和3之间 C.3和4之间 D.4和5之间
4.[2024年福建中考真题]下列实数中,无理数是( )
A. B.0 C. D.
5.[2024年宁夏中考真题]下列各数中,无理数是( )
A.-1 B. C. D.π
6.[2024年四川巴中中考真题]在0,1,,中最小的实数是( )
A.0 B. C.1 D.
7.[2024年青海中考真题]-8的立方根是________.
8.[2024年四川巴中中考真题]27的立方根为__________.
9.[2024年山西中考真题]比较大小:________2(填“>”“<”或“=”).
答案以及解析
对接中考
1.答案:B
解析:根据题意得:,
则正方形的边长为5,
故选: B.
2.答案:A
解析:,,估计的值在2和3之间.
3.答案:C
解析:,
,
即在3和4之间,
故选:C.
4.答案:D
解析:-3,0是整数,是分数,它们不是无理数;5是无限不循环小数,它是无理数,
故选D.
5.答案:D
解析:,是整数,是分数,它们不是无理数;
是无限不循环小数,它是无理数;
故选:D.
6.答案:B
解析:,
最小的实数是,
故选:B.
7.答案:-2
解析:,
的立方根是.
答案:-2.
8.答案:3
解析:,
的立方根是3,
故答案为:3.
9.答案:>
解析:,,
,
,
故答案为:>.
同课章节目录
