2024-2025学年五年级数学下册期末备考真题分类汇编(北京专版)填空题(一)【答案+解析】
文档属性
| 名称 | 2024-2025学年五年级数学下册期末备考真题分类汇编(北京专版)填空题(一)【答案+解析】 |  | |
| 格式 | docx | ||
| 文件大小 | 528.3KB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 北京版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2025-05-29 07:55:01 | ||
图片预览



文档简介
2024-2025学年五年级数学下册期末备考真题分类汇编(北京专版)
填空题(一)
一、填空题
1.(2024五下·门头沟期末)典典在文献阅读的过程中,遇到了一些表达年龄称谓的词,如“花甲”、“古稀”、“耄(mào)耋(dié)”……经过查阅,典典了解到:六十岁为“花甲”,七十岁为“古稀”,八九十岁为“耄(mào)耋(dié)”。典典)岁。的爷爷已过古稀,未及耄,且年龄既是2的倍数又有因数3,典典的爷爷最小 岁。
2.(2024五下·门头沟期末)如下图所示,张老师把一些体积为1cm3的小正方体摆放在个长方体盒子中,一共可以摆放 个这样的小正方体,这个长方体盒子的棱长总和是 cm。
3.(2024五下·门头沟期末)春暖花开,亮亮和爷爷一起栽花。他们把一袋5千克的花土平均分装在6个花盆中,每个花盆中的土占这袋土的 ,每个花盆里放了 千克的土。
4.(2024五下·门头沟期末)为了降低包装成本,某糕点厂简化了一款糕点的包装盒,使包装盒的盒壁变薄,如右图所示,包装盒的体积 ,容积 (请选填:变大、变小、不变)
5.(2024五下·门头沟期末)一个由若干个同样的小正方体摆成的几何体,从正面看是,从左面看是,摆成这样的几何体最少用 个小正方体,最多用 个小正方体。
6.(2024五下·门头沟期末)用下图中的台秤称量 kg 的物品,指针会顺时针旋转 90°。
如果称量 4kg的物品,指针会顺时针旋转 度。
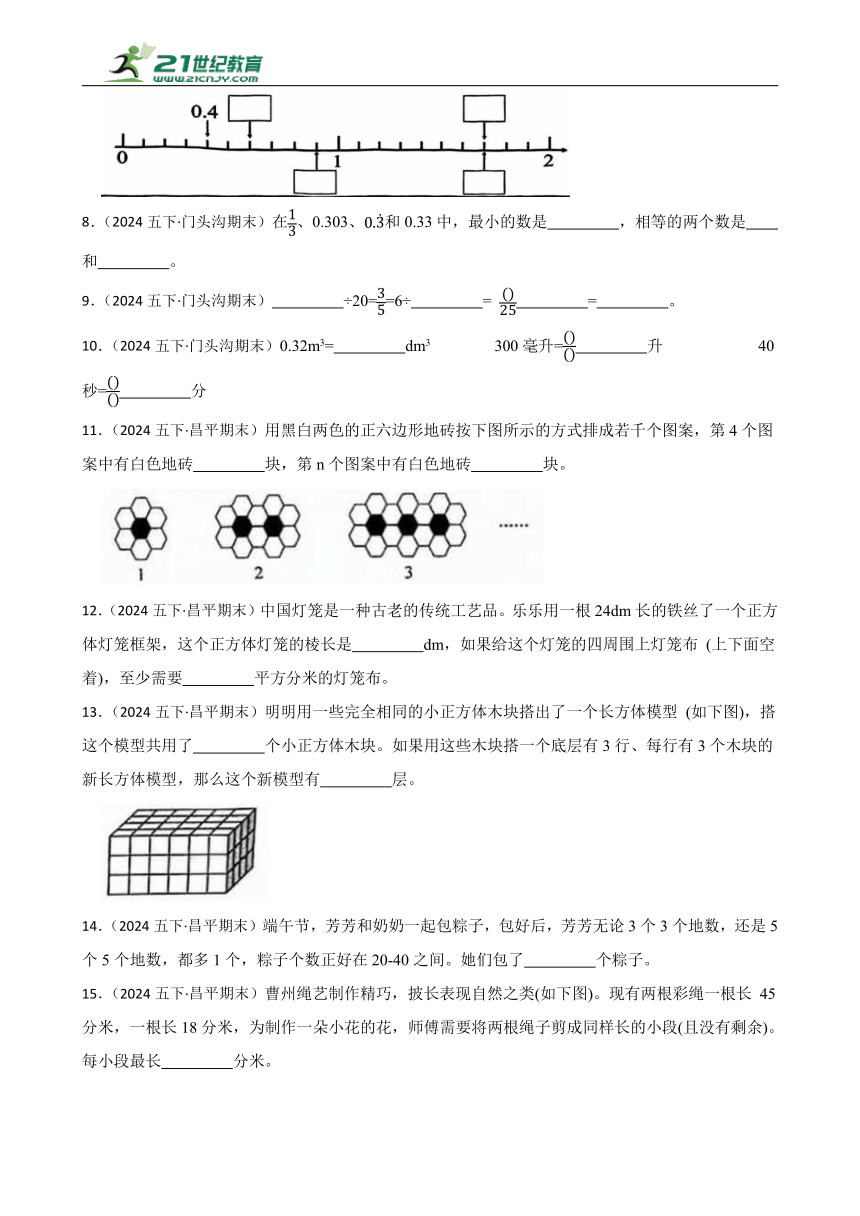
7.(2024五下·门头沟期末)在直线上面的里填上适当的小数,在直线下面的里填上适当的分数。
8.(2024五下·门头沟期末)在、0.303、和0.33中,最小的数是 ,相等的两个数是 和 。
9.(2024五下·门头沟期末) ÷20==6÷ = = 。
10.(2024五下·门头沟期末)0.32m3= dm3 300毫升= 升 40秒= 分
11.(2024五下·昌平期末)用黑白两色的正六边形地砖按下图所示的方式排成若千个图案,第4个图案中有白色地砖 块,第n个图案中有白色地砖 块。
12.(2024五下·昌平期末)中国灯笼是一种古老的传统工艺品。乐乐用一根24dm长的铁丝了一个正方体灯笼框架,这个正方体灯笼的棱长是 dm,如果给这个灯笼的四周围上灯笼布 (上下面空着),至少需要 平方分米的灯笼布。
13.(2024五下·昌平期末)明明用一些完全相同的小正方体木块搭出了一个长方体模型 (如下图),搭这个模型共用了 个小正方体木块。如果用这些木块搭一个底层有3行、每行有3个木块的新长方体模型,那么这个新模型有 层。
14.(2024五下·昌平期末)端午节,芳芳和奶奶一起包粽子,包好后,芳芳无论3个3个地数,还是5个5个地数,都多1个,粽子个数正好在20-40之间。她们包了 个粽子。
15.(2024五下·昌平期末)曹州绳艺制作精巧,披长表现自然之类(如下图)。现有两根彩绳一根长 45分米,一根长18分米,为制作一朵小花的花,师傅需要将两根绳子剪成同样长的小段(且没有剩余)。每小段最长 分米。
16.(2024五下·昌平期末)某品牌的空调外机可近似看成长方体,长约900mm,宽约400mm,高约700mm,这款空调外机占据的空间约为 dm3
17.(2024五下·昌平期末)把一根长5米的丝带平均分成8段,每段占这根丝带的 ,每段长 米。
18.(2024五下·昌平期末) =3÷4= =9÷ = (填小数)。
19.(2024五下·昌平期末)5020cm3= dm3 8.6L= L mL
20.(2024五下·期末)在一次朗诵比赛中,几位评委给笑笑打的分数如下。(满分100分)
去掉一个最高分、去掉一个最低分,将余下的4个分数的平均数作为选手的最终成绩。笑笑的最终成绩是 分。
21.(2024五下·期末)在里填上“>”” <”或”=”
22.(2024五下·期末)一根绳子长 12m ,如果每m 截一段,可以截 段。
23.(2024五下·期末)0.9dm3= cm3
83mL= L
2325cm3= mL
0.47dm3= mL
24.(2024五下·期末)= = = ÷40= (填小数)
25.(2024五下·朝阳期末)根据航空公司的规定,乘坐飞机时随身行李和托运行李的尺寸要求如下图,随身行李箱的体积是 立方厘米。
26.(2024五下·朝阳期末)一杯纯果汁,小亮喝了半杯后,兑满水又喝了杯,他一共喝水 杯。
27.(2024五下·朝阳期末)端午节是每年的农历五月初五,是我国首个入选非遗的节日。端午节前夕,圆圆家一共包了 24 个蛋黄粽和 36 个蜜枣粽,他们想把粽子分装成礼盒送给亲朋好友品尝。如果每盒里都有这两种口味的粽子,且分完后都没有剩余,他们最多能分装出 个同样的粽子礼盒。
28.(2024五下·朝阳期末)把、0.63、和 这四个数按照从大到小的顺序排列, 。
29.(2024五下·朝阳期末)= 6÷ = = (填小数)
30.(2024五下·东城期末)一杯纯果汁,李强喝了杯后,兑满水又喝了一半。李强一共喝了 杯纯果汁, 杯水。
31.(2024五下·东城期末)下图是冰雪大世界冰灯展区的一个冰雕作品“数字 0”,它的体积是 立方分米。(单位:分米)
32.(2024五下·东城期末)为了弘扬中华传统文化,少年宫开设了古诗词鉴资班。王红每3天上一次唐诗鉴赏班,张亮每隔5天上一次宋词鉴资班。2024年4月1日是两人同一天学习古诗词的日子,4月里他们共有 次同一天学习古诗词。
33.(2024五下·东城期末)一个几何体从上面看是,从左面看是,要搭成这样的几何体至少要用 个小正方体,最多可以用 个小正方体。
34.(2024五下·东城期末)在下面每组的里填上“>” “<” 或“=”
35.(2024五下·东城期末)3÷4= = = (填小数)
36.(2024五下·东城期末)350cm3= dm3 2.08L= mL
37.(2024五下·房山期末)《庄子·天下》中有一句话:“一尺之捶,日取其半,万世不竭。”意思就是:一根一尺(尺,我国古代长度单位)长的木,第一天取它的一半,第二天取剩下的一半,第三天继续取剩下的一半……这样取下去,永远也取不尽。第四天取的长度是这根木棒的 。(填分数)
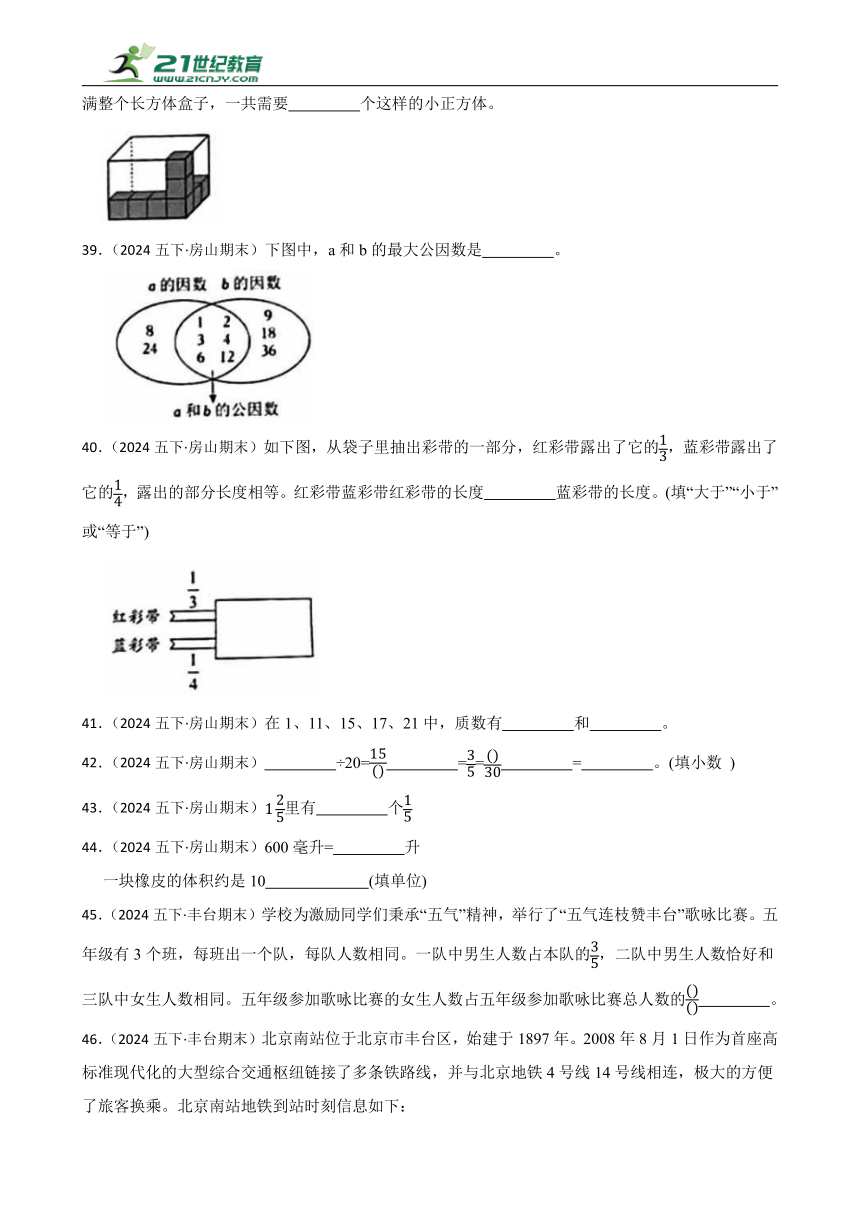
38.(2024五下·房山期末)如下图所示,丽丽已经在一个长方体盒子中摆了8个小正方体,如果要摆满整个长方体盒子,一共需要 个这样的小正方体。
39.(2024五下·房山期末)下图中,a和b的最大公因数是 。
40.(2024五下·房山期末)如下图,从袋子里抽出彩带的一部分,红彩带露出了它的,蓝彩带露出了它的,露出的部分长度相等。红彩带蓝彩带红彩带的长度 蓝彩带的长度。(填“大于”“小于”或“等于”)
41.(2024五下·房山期末)在1、11、15、17、21中,质数有 和 。
42.(2024五下·房山期末) ÷20= == = 。(填小数 )
43.(2024五下·房山期末)里有 个
44.(2024五下·房山期末)600毫升= 升
一块橡皮的体积约是10 (填单位)
45.(2024五下·丰台期末)学校为激励同学们秉承“五气”精神,举行了“五气连枝赞丰台”歌咏比赛。五年级有3个班,每班出一个队,每队人数相同。一队中男生人数占本队的,二队中男生人数恰好和三队中女生人数相同。五年级参加歌咏比赛的女生人数占五年级参加歌咏比赛总人数的 。
46.(2024五下·丰台期末)北京南站位于北京市丰台区,始建于1897年。2008年8月1日作为首座高标准现代化的大型综合交通枢纽链接了多条铁路线,并与北京地铁4号线14号线相连,极大的方便了旅客换乘。北京南站地铁到站时刻信息如下:
根据地铁到站时刻表,这两条地铁线路在早高峰8时至10时期间,同时到达北京南站的次数有 次。
47.(2024五下·丰台期末)兰兰做了一个测量铁球体积的实验:
第一步,将 800毫升的水倒入一个容积1升的杯子中;
第二步,将5个相同的铁球放入水中,杯中的水没有满;
第三步,再将1个同样的铁球放入水中,这时杯中的水溢出10毫升
根据这个实验,可以知道一个铁球的体积是 立方厘米。
48.(2024五下·丰台期末)学校门厅有一个长 20分米,宽12分米的长方形宣传栏。如果把同学们用完全相同的正方形纸完成的书画作品,既不重叠、也无缝隙地正好贴满宣传栏,正方形纸的边长最大是 分米。
49.(2024五下·丰台期末)在上面的括号里填上分数,在下面的括号里填上小数。
50.(2024五下·丰台期末)把一桶 5kg花生油平均装在3个瓶子里,每个瓶子能装 kg花生油,每个瓶子能装这桶花生油的 。
答案解析部分
1.72
解:在71岁到79岁的范围内,既是2的倍数又是3的倍数的年龄是72岁。因为72岁既是偶数(2的倍数),同时72也能被3整除(7+2=9,9可以被3整除)。所以,根据题目的条件,典典的爷爷最小可能是72岁。
故答案为:72。
根据题干信息,典典的爷爷已过古稀,即年龄大于70岁;且未及耄耋,即年龄小于80岁。因此,爷爷的年龄范围是71岁到79岁。同时,题目要求爷爷的年龄既是2的倍数又是3的倍数。这就需要我们在这一个年龄范围内,找出同时满足这两个条件的年龄。
2.96;56
解:6×4×4
=24×4
=96(个)
(6+4+4)×4
=14×4
=56(厘米)。
故答案为:96;56。
一共可以摆放这样小正方体的个数=长边的个数×宽边的个数×高边的个数;这个长方体盒子的棱长总和=(长+宽+高)×4。
3.;
解:1÷6=
5÷6=(千克)。
故答案为:;。
每个花盆中的土占这袋土的分率=1÷平均分装花盆的个数,每个花盆里放的质量=花土的总质量÷平均分装花盆的个数。
4.变小;不变
解:由于包装盒的盒壁变薄,包装盒的体积确实变小了,但是包装盒的容积是指包装盒所能容纳物体的体积,这个空间并没有因为盒壁的变薄而改变,所以包装盒的容积是不变的。
故答案为:变小;不变。
物体所占空间的大小叫做它的体积,容器所能容纳物体的体积叫做它的容积,使包装盒的盒壁变薄后,包装盒的体积变小,容积不变。
5.3;6
解: 摆成这样的几何体最少用3个小正方体,最多用6个小正方体。
故答案为:3;6。
用正方体最少时,左边一列有2个正方体,右边一列1个正方体,共3个;
用正方体最多时,左边一列有3个正方体,右边一列3个正方体,共6个。
6.2;180
解:360°÷8=45°,90°÷45°=2(格),下图中的台秤称量2千克的物品,指针会顺时针旋转 90°;
如果称量4千克的物品,指针会顺时针旋转45°×4=180°。
故答案为:2;180。
平均每个格表示的度数=周角÷总格数,台秤称量2千克的物品,指针会顺时针旋转 90°;如果称量4千克的物品,指针会顺时针旋转的度数=平均每个格表示的度数×格数。
7.解:
把单位“1”平均分成10份,每份是0.1或者,几份的地方就是十分之几。
8.0.303;;
解:=1÷3=
=>0.33>0.303,最小的数是0.303,相等的两个数是和。
故答案为:0.303;;。
分数化成小数,用分数的分子除以分母,然后再比较大小。
9.12;10;15;0.6
解:=(3×4)÷(5×4)=12÷20;
=(3×2)÷(5×2)=6÷10;
==;
=3÷5=0.6;
所以12÷20==6÷10==0.6。
故答案为:12;10;15;0.6。
分数的基本性质:分数的分子和分母同时乘或除以同一个不为0的数,分数的大小不变。
分数与除法的关系,被除数作分子,除数作分母。
10.320;;
解:0.32×1000=320(立方分米);
300÷1000=(升);
40÷60=(分)。
故答案为:320;;。
单位换算,从高级单位到低级单位,用高级单位的数乘进率;从低级单位到高级单位,用低级单位的数除以进率。
11.18;4n+2
解:4×4+2
=16+2
=18(块)
4×n+2=(4n+2)(块)。
故答案为:18;(4n+2)。
第n个图形中有白色地砖的块数=(4n+2)块。
12.2;16
解:24÷12=2(分米)
2×2×4
=4×4
=16(平方分米)。
故答案为:2;16。
这个正方体灯笼的棱长=铁丝的长÷12,至少需要灯笼布的面积=棱长×棱长×4。
13.72;8
解:6×4×3
=24×3
=72(个)
72÷3÷3
=24÷3
=8(层)。
故答案为:72;8。
搭这个模型共用小正方体木块的块数=长边用的块数×宽边用的块数×高边用的块数;这个新模型的层数=总块数÷底层的行数÷平均每行的个数。
14.31
解:3×5×2+1
=15×2+1
=30+1
=31(个)。
故答案为:31。
她们包粽子的总个数=3和5的最小公倍数×2+1个。
15.9
解:,45和18的最大公因数是3×3=9。
故答案为:9。
每小段最长的长度=45和18的最大公因数,用短除法求出。
16.252
解:900毫米=9分米
400毫米=4分米
700毫米=7分米
9×4×7
=36×7
=252(立方分米)。
故答案为:252。
这款空调外机占据的空间=长×宽×高。
17.;
解:1÷8=
5÷8=(米)。
故答案为:;。
每段占这根丝带的分率=1÷平均分的段数,每段的长度=丝带的总长度÷平均分的段数。
18.15;24;12;0.75
解:3÷4===;
==;
3÷4=(3×3)÷(4×3)=9÷12;
3÷4=0.75;
所以=3÷4==9÷12=0.75。
故答案为:15;24;12;0.75。
分数的基本性质:分数的分子和分母同时乘或除以同一个不为0的数,分数的大小不变。
分数与除法的关系,被除数作分子,除数作分母。
19.5.02;8;600
解:5020÷1000=5.02(立方分米);
(8.6-8)×1000
=0.6×1000
=600(毫升),所以8.6升=8升600毫升。
故答案为:5.02;8;600。
单位换算,从高级单位到低级单位,用高级单位的数乘进率;从低级单位到高级单位,用低级单位的数除以进率。
20.96.5
解:(95+96+97+98)÷4
=386÷4
=96.5(分)。
故答案为:96.5。
笑笑的最终成绩=去掉一个最高分、去掉一个最低分后剩余分数的和÷4。
21.
解:因为<1,所以<;
因为<1,<,>,所以×<;
因为a>1,所以>。
故答案为:<;<;>。
一个数(0和负数除外)除以小于1的数,所得的商大于原来的数;反之,商小于原来的数;一个数(0和负数除外)乘小于1的数,所得的积小于原来的数,反之,积大于原来的数。
22.18
解:12÷=18(段)。
故答案为:18。
可以截的段数=绳子的总长÷平均每段的长度。
23.900;0.083;2325;470
解:0.9×1000=900(立方厘米);
83÷1000=0.083(升),所以83毫升=0.083升;
2325立方厘米=2325毫升;
0.47×1000=470(毫升)。
故答案为:900;0.083;2325;470。
单位换算,从高级单位到低级单位,用高级单位的数乘进率;从低级单位到高级单位,用低级单位的数除以进率。
24.9;32;15;0.375
解:==;
==;
=(3×5)÷(8×5)=15÷40;
=3÷8=0.375;
所以===15÷40=0.375。
故答案为:9;32;15;0.375。
分数的基本性质:分数的分子和分母同时乘或除以同一个不为0的数,分数的大小不变
分数化成小数,用分数的分子除以分母。
25.44000
解:40×55×20
=2200×20
=44000(立方厘米)。
故答案为:44000。
随身行李箱的体积=长×宽×高。
26.
解:1-=(杯),杯的是杯。
故答案为:。
一杯纯果汁,小亮喝了半杯后,则兑水1-=杯,然后他喝的水是杯的即杯。
27.12
解:24和36的最大公因数是2×2×3=12。
故答案为:12。
他们最多能分装出同样粽子礼盒的个数=24和36的最大公因数,用短除法求出。
28.0.63>>>
解:=8÷13≈0.6154;
=5÷8=0.625
所以0.63>>>。
故答案为:0.63>>>。
分数化成小数,用分数的分子除以分母,然后比较大小。
29.16;9;0.375
解:=3÷8=(3×2)÷(8×2)=6÷16;
==;
=3÷8=0.375;
所以=6÷16==0.375。
故答案为:16;9;0.375。
商不变的性质:在除法里,被除数和除数同时扩大或缩小相同的倍数(0除外),商不变;
分数的基本性质:分数的分子和分母同时乘或除以同一个不为0的数,分数的大小不变;
分数化成小数,用分数的分子除以分母。
30.;
解:纯果汁:+=(杯);
水:的是(杯)。
故答案为:;。
共喝纯果汁的杯数=先喝的杯+又喝的(1-)的也就是杯;
共喝水的杯数=的是杯。
31.56
解:6×2×10-4×2×8
=120-64
=56(立方分米)。
故答案为:56。
它的体积=整个长方体的长×宽×高-中间空余部分的长×宽×高。
32.2
解:3×5=15(天)
1+15=16(日),共2次。
故答案为:2。
先求出3和5的最小公倍数是3×5=15天,也就是王红和张亮最少每隔15天同时上一次宋词鉴赏班,4月有30天,4月1日是第一次,4月16日是第二次,第三次就是5月1日了,所以4月里他们共有2次同一天学习古诗词。
33.5;7
解:
4+1=5(个);4+3=7(个)。
故答案为:5;7。
这个立体图形最少时,下面一层4个小正方体,上面一层1个小正方体,在后面一排的任何一个上面;这个立体图形最多时,下面一层4个小正方体,上面一层3个小正方体,在后面一排的任何一个上面.
34. 3 3.34
=,所以<;
3=,所以3>;
==,所以=;
=3+17÷50=3.34,所以=3.34。
故答案为:<;>;=;=。
分数的基本性质:分数的分子和分母同时乘或除以同一个不为0的数,分数的大小不变;
分数比较大小,同分母分数,分子大的就大;同分子分数,分母小的就大;异分母分数比较大小,先通分,然后按照同分母分数比较大小的方法比较大小。
35.8;18;0.75
解:3÷4=0.75;
3÷4=====;
所以3÷4===0.75。
故答案为:8;18;0.75。
分数化成小数,用分数的分子除以分母;
分数的基本性质:分数的分子和分母同时乘或除以同一个不为0的数,分数的大小不变;
分数与除法的关系,被除数作分子,除数作分母。
36.0.35;2080
解:350÷1000=0.35(立方分米);
2.08×1000=2080(毫升)。
故答案为:0.35;2080。
单位换算,从高级单位到低级单位,用高级单位的数乘进率;从低级单位到高级单位,用低级单位的数除以进率。
37.
解:2×2×2×2=16
1÷16=。
故答案为:。
第四天取的长度相当于把这根木棒平均分成16份,取其中的1份,是。
38.36
解:4×3×3
=12×3
=36(个)。
故答案为:36。
一共需要这样小正方体的个数=长边需要的个数×宽边需要的个数×高边需要的个数。
39.12
解:a和b的公因数有1、2、3、4、6、12,所以最大公因数是12。
故答案为:12。
两个数的因数中,最大的一个是最大公因数。
40.小于
解:>,所以红彩带的长度小于蓝彩带的长度。
故答案为:小于。
因为红彩带露出的分率大于蓝彩带露出的分率,并且露出部分长度相等,所以红彩带的长度小于蓝彩带的长度。
41.11;17
解:在1、11、15、17、21中,质数有11和17。
故答案为:11;17。
依据100以内的质数表填空。
42.12;25;18;0.6
解:=(3×4)÷(5×4)=12÷20;
==;
==;
=3÷5=0.6;
所以12÷20====0.6。
故答案为:12;25;18;0.6。
分数的基本性质:分数的分子和分母同时乘或除以同一个不为0的数,分数的大小不变;
分数与除法的关系,被除数作分子,除数作分母;
分数化成小数,用分数的分子除以分母。
43.7
解:=,里面有7个。
故答案为:7。
分数中的分母表示把单位“1”平均分的份数,分子表示取的份数,分子是几,就表示有几个这样的分数单位。
44.0.6;立方厘米
解:600÷1000=0.6(升),所以600毫升=0.6升;
一块橡皮的体积约是10立方厘米。
故答案为:0.6;立方厘米。
单位换算,从高级单位到低级单位,用高级单位的数乘进率;从低级单位到高级单位,用低级单位的数除以进率;
根据实际生活经验以及题干中的具体数据来进行填空。
45.
解:1-=
×=
1÷2×(1-)
=×
=
+=。
故答案为:。
每队人数相同,并且二队男生人数=三队女生人数,则二队女生人数=三队男生人数(每队人数=男生+女生),那么二队男生人数+三队男生人数=二队女生人数+三队女生人数,一队女生占本队人数的:1-=;一队女生占总人数的×=,二、三队女生占总人数的:1÷2×(1-)=,然后再相加。
46.20
解:3-1=2(分钟)
4-1=3(分钟)
2×3=6(分钟)
60×(10-8)
=60×2
=120(分)
120÷6=20(次)。
故答案为:20。
北京地铁4号线每2分钟到达一次,14号线每3分钟到达一次,这两条线同时到达北京南站的间隔时间是2和3的最小公倍数,这两条线同时到达北京南站的次数=(10时-8时)×平均每小时的分钟数÷这两条线同时到达北京南站的间隔时间。
47.35
解:1升=1000毫升
(1000+10-800)÷(5+1)
=210÷6
=35(毫升)
35毫升=35立方厘米。
故答案为:35。
一个铁球的体积=(杯子的容积+溢出水的体积-倒入水的体积) ÷(先放入铁球的个数+又放入铁球的个数)。
48.4
解:20和12的最大公因数是2×2=4,则正方形纸的边长最大是4分米。
故答案为:4。
正方形纸的边长最大是20和12的最大公因数,可以用短除法求出。
49.;;0.75;1.25
解:1÷4=,7÷4=,3÷4=0.75,5÷4=1.25。
故答案为:;;0.75;1.25。
把单位“1”平均分成4份,每份是,几份就是几除以4。
50.;
解:5÷3=(千克)
1÷3=。
故答案为:;。
每个瓶子能装的质量=花生油的总质量÷平均装的瓶数;每个瓶子能装这桶花生油的分率=1÷平均装的瓶数。
填空题(一)
一、填空题
1.(2024五下·门头沟期末)典典在文献阅读的过程中,遇到了一些表达年龄称谓的词,如“花甲”、“古稀”、“耄(mào)耋(dié)”……经过查阅,典典了解到:六十岁为“花甲”,七十岁为“古稀”,八九十岁为“耄(mào)耋(dié)”。典典)岁。的爷爷已过古稀,未及耄,且年龄既是2的倍数又有因数3,典典的爷爷最小 岁。
2.(2024五下·门头沟期末)如下图所示,张老师把一些体积为1cm3的小正方体摆放在个长方体盒子中,一共可以摆放 个这样的小正方体,这个长方体盒子的棱长总和是 cm。
3.(2024五下·门头沟期末)春暖花开,亮亮和爷爷一起栽花。他们把一袋5千克的花土平均分装在6个花盆中,每个花盆中的土占这袋土的 ,每个花盆里放了 千克的土。
4.(2024五下·门头沟期末)为了降低包装成本,某糕点厂简化了一款糕点的包装盒,使包装盒的盒壁变薄,如右图所示,包装盒的体积 ,容积 (请选填:变大、变小、不变)
5.(2024五下·门头沟期末)一个由若干个同样的小正方体摆成的几何体,从正面看是,从左面看是,摆成这样的几何体最少用 个小正方体,最多用 个小正方体。
6.(2024五下·门头沟期末)用下图中的台秤称量 kg 的物品,指针会顺时针旋转 90°。
如果称量 4kg的物品,指针会顺时针旋转 度。
7.(2024五下·门头沟期末)在直线上面的里填上适当的小数,在直线下面的里填上适当的分数。
8.(2024五下·门头沟期末)在、0.303、和0.33中,最小的数是 ,相等的两个数是 和 。
9.(2024五下·门头沟期末) ÷20==6÷ = = 。
10.(2024五下·门头沟期末)0.32m3= dm3 300毫升= 升 40秒= 分
11.(2024五下·昌平期末)用黑白两色的正六边形地砖按下图所示的方式排成若千个图案,第4个图案中有白色地砖 块,第n个图案中有白色地砖 块。
12.(2024五下·昌平期末)中国灯笼是一种古老的传统工艺品。乐乐用一根24dm长的铁丝了一个正方体灯笼框架,这个正方体灯笼的棱长是 dm,如果给这个灯笼的四周围上灯笼布 (上下面空着),至少需要 平方分米的灯笼布。
13.(2024五下·昌平期末)明明用一些完全相同的小正方体木块搭出了一个长方体模型 (如下图),搭这个模型共用了 个小正方体木块。如果用这些木块搭一个底层有3行、每行有3个木块的新长方体模型,那么这个新模型有 层。
14.(2024五下·昌平期末)端午节,芳芳和奶奶一起包粽子,包好后,芳芳无论3个3个地数,还是5个5个地数,都多1个,粽子个数正好在20-40之间。她们包了 个粽子。
15.(2024五下·昌平期末)曹州绳艺制作精巧,披长表现自然之类(如下图)。现有两根彩绳一根长 45分米,一根长18分米,为制作一朵小花的花,师傅需要将两根绳子剪成同样长的小段(且没有剩余)。每小段最长 分米。
16.(2024五下·昌平期末)某品牌的空调外机可近似看成长方体,长约900mm,宽约400mm,高约700mm,这款空调外机占据的空间约为 dm3
17.(2024五下·昌平期末)把一根长5米的丝带平均分成8段,每段占这根丝带的 ,每段长 米。
18.(2024五下·昌平期末) =3÷4= =9÷ = (填小数)。
19.(2024五下·昌平期末)5020cm3= dm3 8.6L= L mL
20.(2024五下·期末)在一次朗诵比赛中,几位评委给笑笑打的分数如下。(满分100分)
去掉一个最高分、去掉一个最低分,将余下的4个分数的平均数作为选手的最终成绩。笑笑的最终成绩是 分。
21.(2024五下·期末)在里填上“>”” <”或”=”
22.(2024五下·期末)一根绳子长 12m ,如果每m 截一段,可以截 段。
23.(2024五下·期末)0.9dm3= cm3
83mL= L
2325cm3= mL
0.47dm3= mL
24.(2024五下·期末)= = = ÷40= (填小数)
25.(2024五下·朝阳期末)根据航空公司的规定,乘坐飞机时随身行李和托运行李的尺寸要求如下图,随身行李箱的体积是 立方厘米。
26.(2024五下·朝阳期末)一杯纯果汁,小亮喝了半杯后,兑满水又喝了杯,他一共喝水 杯。
27.(2024五下·朝阳期末)端午节是每年的农历五月初五,是我国首个入选非遗的节日。端午节前夕,圆圆家一共包了 24 个蛋黄粽和 36 个蜜枣粽,他们想把粽子分装成礼盒送给亲朋好友品尝。如果每盒里都有这两种口味的粽子,且分完后都没有剩余,他们最多能分装出 个同样的粽子礼盒。
28.(2024五下·朝阳期末)把、0.63、和 这四个数按照从大到小的顺序排列, 。
29.(2024五下·朝阳期末)= 6÷ = = (填小数)
30.(2024五下·东城期末)一杯纯果汁,李强喝了杯后,兑满水又喝了一半。李强一共喝了 杯纯果汁, 杯水。
31.(2024五下·东城期末)下图是冰雪大世界冰灯展区的一个冰雕作品“数字 0”,它的体积是 立方分米。(单位:分米)
32.(2024五下·东城期末)为了弘扬中华传统文化,少年宫开设了古诗词鉴资班。王红每3天上一次唐诗鉴赏班,张亮每隔5天上一次宋词鉴资班。2024年4月1日是两人同一天学习古诗词的日子,4月里他们共有 次同一天学习古诗词。
33.(2024五下·东城期末)一个几何体从上面看是,从左面看是,要搭成这样的几何体至少要用 个小正方体,最多可以用 个小正方体。
34.(2024五下·东城期末)在下面每组的里填上“>” “<” 或“=”
35.(2024五下·东城期末)3÷4= = = (填小数)
36.(2024五下·东城期末)350cm3= dm3 2.08L= mL
37.(2024五下·房山期末)《庄子·天下》中有一句话:“一尺之捶,日取其半,万世不竭。”意思就是:一根一尺(尺,我国古代长度单位)长的木,第一天取它的一半,第二天取剩下的一半,第三天继续取剩下的一半……这样取下去,永远也取不尽。第四天取的长度是这根木棒的 。(填分数)
38.(2024五下·房山期末)如下图所示,丽丽已经在一个长方体盒子中摆了8个小正方体,如果要摆满整个长方体盒子,一共需要 个这样的小正方体。
39.(2024五下·房山期末)下图中,a和b的最大公因数是 。
40.(2024五下·房山期末)如下图,从袋子里抽出彩带的一部分,红彩带露出了它的,蓝彩带露出了它的,露出的部分长度相等。红彩带蓝彩带红彩带的长度 蓝彩带的长度。(填“大于”“小于”或“等于”)
41.(2024五下·房山期末)在1、11、15、17、21中,质数有 和 。
42.(2024五下·房山期末) ÷20= == = 。(填小数 )
43.(2024五下·房山期末)里有 个
44.(2024五下·房山期末)600毫升= 升
一块橡皮的体积约是10 (填单位)
45.(2024五下·丰台期末)学校为激励同学们秉承“五气”精神,举行了“五气连枝赞丰台”歌咏比赛。五年级有3个班,每班出一个队,每队人数相同。一队中男生人数占本队的,二队中男生人数恰好和三队中女生人数相同。五年级参加歌咏比赛的女生人数占五年级参加歌咏比赛总人数的 。
46.(2024五下·丰台期末)北京南站位于北京市丰台区,始建于1897年。2008年8月1日作为首座高标准现代化的大型综合交通枢纽链接了多条铁路线,并与北京地铁4号线14号线相连,极大的方便了旅客换乘。北京南站地铁到站时刻信息如下:
根据地铁到站时刻表,这两条地铁线路在早高峰8时至10时期间,同时到达北京南站的次数有 次。
47.(2024五下·丰台期末)兰兰做了一个测量铁球体积的实验:
第一步,将 800毫升的水倒入一个容积1升的杯子中;
第二步,将5个相同的铁球放入水中,杯中的水没有满;
第三步,再将1个同样的铁球放入水中,这时杯中的水溢出10毫升
根据这个实验,可以知道一个铁球的体积是 立方厘米。
48.(2024五下·丰台期末)学校门厅有一个长 20分米,宽12分米的长方形宣传栏。如果把同学们用完全相同的正方形纸完成的书画作品,既不重叠、也无缝隙地正好贴满宣传栏,正方形纸的边长最大是 分米。
49.(2024五下·丰台期末)在上面的括号里填上分数,在下面的括号里填上小数。
50.(2024五下·丰台期末)把一桶 5kg花生油平均装在3个瓶子里,每个瓶子能装 kg花生油,每个瓶子能装这桶花生油的 。
答案解析部分
1.72
解:在71岁到79岁的范围内,既是2的倍数又是3的倍数的年龄是72岁。因为72岁既是偶数(2的倍数),同时72也能被3整除(7+2=9,9可以被3整除)。所以,根据题目的条件,典典的爷爷最小可能是72岁。
故答案为:72。
根据题干信息,典典的爷爷已过古稀,即年龄大于70岁;且未及耄耋,即年龄小于80岁。因此,爷爷的年龄范围是71岁到79岁。同时,题目要求爷爷的年龄既是2的倍数又是3的倍数。这就需要我们在这一个年龄范围内,找出同时满足这两个条件的年龄。
2.96;56
解:6×4×4
=24×4
=96(个)
(6+4+4)×4
=14×4
=56(厘米)。
故答案为:96;56。
一共可以摆放这样小正方体的个数=长边的个数×宽边的个数×高边的个数;这个长方体盒子的棱长总和=(长+宽+高)×4。
3.;
解:1÷6=
5÷6=(千克)。
故答案为:;。
每个花盆中的土占这袋土的分率=1÷平均分装花盆的个数,每个花盆里放的质量=花土的总质量÷平均分装花盆的个数。
4.变小;不变
解:由于包装盒的盒壁变薄,包装盒的体积确实变小了,但是包装盒的容积是指包装盒所能容纳物体的体积,这个空间并没有因为盒壁的变薄而改变,所以包装盒的容积是不变的。
故答案为:变小;不变。
物体所占空间的大小叫做它的体积,容器所能容纳物体的体积叫做它的容积,使包装盒的盒壁变薄后,包装盒的体积变小,容积不变。
5.3;6
解: 摆成这样的几何体最少用3个小正方体,最多用6个小正方体。
故答案为:3;6。
用正方体最少时,左边一列有2个正方体,右边一列1个正方体,共3个;
用正方体最多时,左边一列有3个正方体,右边一列3个正方体,共6个。
6.2;180
解:360°÷8=45°,90°÷45°=2(格),下图中的台秤称量2千克的物品,指针会顺时针旋转 90°;
如果称量4千克的物品,指针会顺时针旋转45°×4=180°。
故答案为:2;180。
平均每个格表示的度数=周角÷总格数,台秤称量2千克的物品,指针会顺时针旋转 90°;如果称量4千克的物品,指针会顺时针旋转的度数=平均每个格表示的度数×格数。
7.解:
把单位“1”平均分成10份,每份是0.1或者,几份的地方就是十分之几。
8.0.303;;
解:=1÷3=
=>0.33>0.303,最小的数是0.303,相等的两个数是和。
故答案为:0.303;;。
分数化成小数,用分数的分子除以分母,然后再比较大小。
9.12;10;15;0.6
解:=(3×4)÷(5×4)=12÷20;
=(3×2)÷(5×2)=6÷10;
==;
=3÷5=0.6;
所以12÷20==6÷10==0.6。
故答案为:12;10;15;0.6。
分数的基本性质:分数的分子和分母同时乘或除以同一个不为0的数,分数的大小不变。
分数与除法的关系,被除数作分子,除数作分母。
10.320;;
解:0.32×1000=320(立方分米);
300÷1000=(升);
40÷60=(分)。
故答案为:320;;。
单位换算,从高级单位到低级单位,用高级单位的数乘进率;从低级单位到高级单位,用低级单位的数除以进率。
11.18;4n+2
解:4×4+2
=16+2
=18(块)
4×n+2=(4n+2)(块)。
故答案为:18;(4n+2)。
第n个图形中有白色地砖的块数=(4n+2)块。
12.2;16
解:24÷12=2(分米)
2×2×4
=4×4
=16(平方分米)。
故答案为:2;16。
这个正方体灯笼的棱长=铁丝的长÷12,至少需要灯笼布的面积=棱长×棱长×4。
13.72;8
解:6×4×3
=24×3
=72(个)
72÷3÷3
=24÷3
=8(层)。
故答案为:72;8。
搭这个模型共用小正方体木块的块数=长边用的块数×宽边用的块数×高边用的块数;这个新模型的层数=总块数÷底层的行数÷平均每行的个数。
14.31
解:3×5×2+1
=15×2+1
=30+1
=31(个)。
故答案为:31。
她们包粽子的总个数=3和5的最小公倍数×2+1个。
15.9
解:,45和18的最大公因数是3×3=9。
故答案为:9。
每小段最长的长度=45和18的最大公因数,用短除法求出。
16.252
解:900毫米=9分米
400毫米=4分米
700毫米=7分米
9×4×7
=36×7
=252(立方分米)。
故答案为:252。
这款空调外机占据的空间=长×宽×高。
17.;
解:1÷8=
5÷8=(米)。
故答案为:;。
每段占这根丝带的分率=1÷平均分的段数,每段的长度=丝带的总长度÷平均分的段数。
18.15;24;12;0.75
解:3÷4===;
==;
3÷4=(3×3)÷(4×3)=9÷12;
3÷4=0.75;
所以=3÷4==9÷12=0.75。
故答案为:15;24;12;0.75。
分数的基本性质:分数的分子和分母同时乘或除以同一个不为0的数,分数的大小不变。
分数与除法的关系,被除数作分子,除数作分母。
19.5.02;8;600
解:5020÷1000=5.02(立方分米);
(8.6-8)×1000
=0.6×1000
=600(毫升),所以8.6升=8升600毫升。
故答案为:5.02;8;600。
单位换算,从高级单位到低级单位,用高级单位的数乘进率;从低级单位到高级单位,用低级单位的数除以进率。
20.96.5
解:(95+96+97+98)÷4
=386÷4
=96.5(分)。
故答案为:96.5。
笑笑的最终成绩=去掉一个最高分、去掉一个最低分后剩余分数的和÷4。
21.
解:因为<1,所以<;
因为<1,<,>,所以×<;
因为a>1,所以>。
故答案为:<;<;>。
一个数(0和负数除外)除以小于1的数,所得的商大于原来的数;反之,商小于原来的数;一个数(0和负数除外)乘小于1的数,所得的积小于原来的数,反之,积大于原来的数。
22.18
解:12÷=18(段)。
故答案为:18。
可以截的段数=绳子的总长÷平均每段的长度。
23.900;0.083;2325;470
解:0.9×1000=900(立方厘米);
83÷1000=0.083(升),所以83毫升=0.083升;
2325立方厘米=2325毫升;
0.47×1000=470(毫升)。
故答案为:900;0.083;2325;470。
单位换算,从高级单位到低级单位,用高级单位的数乘进率;从低级单位到高级单位,用低级单位的数除以进率。
24.9;32;15;0.375
解:==;
==;
=(3×5)÷(8×5)=15÷40;
=3÷8=0.375;
所以===15÷40=0.375。
故答案为:9;32;15;0.375。
分数的基本性质:分数的分子和分母同时乘或除以同一个不为0的数,分数的大小不变
分数化成小数,用分数的分子除以分母。
25.44000
解:40×55×20
=2200×20
=44000(立方厘米)。
故答案为:44000。
随身行李箱的体积=长×宽×高。
26.
解:1-=(杯),杯的是杯。
故答案为:。
一杯纯果汁,小亮喝了半杯后,则兑水1-=杯,然后他喝的水是杯的即杯。
27.12
解:24和36的最大公因数是2×2×3=12。
故答案为:12。
他们最多能分装出同样粽子礼盒的个数=24和36的最大公因数,用短除法求出。
28.0.63>>>
解:=8÷13≈0.6154;
=5÷8=0.625
所以0.63>>>。
故答案为:0.63>>>。
分数化成小数,用分数的分子除以分母,然后比较大小。
29.16;9;0.375
解:=3÷8=(3×2)÷(8×2)=6÷16;
==;
=3÷8=0.375;
所以=6÷16==0.375。
故答案为:16;9;0.375。
商不变的性质:在除法里,被除数和除数同时扩大或缩小相同的倍数(0除外),商不变;
分数的基本性质:分数的分子和分母同时乘或除以同一个不为0的数,分数的大小不变;
分数化成小数,用分数的分子除以分母。
30.;
解:纯果汁:+=(杯);
水:的是(杯)。
故答案为:;。
共喝纯果汁的杯数=先喝的杯+又喝的(1-)的也就是杯;
共喝水的杯数=的是杯。
31.56
解:6×2×10-4×2×8
=120-64
=56(立方分米)。
故答案为:56。
它的体积=整个长方体的长×宽×高-中间空余部分的长×宽×高。
32.2
解:3×5=15(天)
1+15=16(日),共2次。
故答案为:2。
先求出3和5的最小公倍数是3×5=15天,也就是王红和张亮最少每隔15天同时上一次宋词鉴赏班,4月有30天,4月1日是第一次,4月16日是第二次,第三次就是5月1日了,所以4月里他们共有2次同一天学习古诗词。
33.5;7
解:
4+1=5(个);4+3=7(个)。
故答案为:5;7。
这个立体图形最少时,下面一层4个小正方体,上面一层1个小正方体,在后面一排的任何一个上面;这个立体图形最多时,下面一层4个小正方体,上面一层3个小正方体,在后面一排的任何一个上面.
34. 3 3.34
=,所以<;
3=,所以3>;
==,所以=;
=3+17÷50=3.34,所以=3.34。
故答案为:<;>;=;=。
分数的基本性质:分数的分子和分母同时乘或除以同一个不为0的数,分数的大小不变;
分数比较大小,同分母分数,分子大的就大;同分子分数,分母小的就大;异分母分数比较大小,先通分,然后按照同分母分数比较大小的方法比较大小。
35.8;18;0.75
解:3÷4=0.75;
3÷4=====;
所以3÷4===0.75。
故答案为:8;18;0.75。
分数化成小数,用分数的分子除以分母;
分数的基本性质:分数的分子和分母同时乘或除以同一个不为0的数,分数的大小不变;
分数与除法的关系,被除数作分子,除数作分母。
36.0.35;2080
解:350÷1000=0.35(立方分米);
2.08×1000=2080(毫升)。
故答案为:0.35;2080。
单位换算,从高级单位到低级单位,用高级单位的数乘进率;从低级单位到高级单位,用低级单位的数除以进率。
37.
解:2×2×2×2=16
1÷16=。
故答案为:。
第四天取的长度相当于把这根木棒平均分成16份,取其中的1份,是。
38.36
解:4×3×3
=12×3
=36(个)。
故答案为:36。
一共需要这样小正方体的个数=长边需要的个数×宽边需要的个数×高边需要的个数。
39.12
解:a和b的公因数有1、2、3、4、6、12,所以最大公因数是12。
故答案为:12。
两个数的因数中,最大的一个是最大公因数。
40.小于
解:>,所以红彩带的长度小于蓝彩带的长度。
故答案为:小于。
因为红彩带露出的分率大于蓝彩带露出的分率,并且露出部分长度相等,所以红彩带的长度小于蓝彩带的长度。
41.11;17
解:在1、11、15、17、21中,质数有11和17。
故答案为:11;17。
依据100以内的质数表填空。
42.12;25;18;0.6
解:=(3×4)÷(5×4)=12÷20;
==;
==;
=3÷5=0.6;
所以12÷20====0.6。
故答案为:12;25;18;0.6。
分数的基本性质:分数的分子和分母同时乘或除以同一个不为0的数,分数的大小不变;
分数与除法的关系,被除数作分子,除数作分母;
分数化成小数,用分数的分子除以分母。
43.7
解:=,里面有7个。
故答案为:7。
分数中的分母表示把单位“1”平均分的份数,分子表示取的份数,分子是几,就表示有几个这样的分数单位。
44.0.6;立方厘米
解:600÷1000=0.6(升),所以600毫升=0.6升;
一块橡皮的体积约是10立方厘米。
故答案为:0.6;立方厘米。
单位换算,从高级单位到低级单位,用高级单位的数乘进率;从低级单位到高级单位,用低级单位的数除以进率;
根据实际生活经验以及题干中的具体数据来进行填空。
45.
解:1-=
×=
1÷2×(1-)
=×
=
+=。
故答案为:。
每队人数相同,并且二队男生人数=三队女生人数,则二队女生人数=三队男生人数(每队人数=男生+女生),那么二队男生人数+三队男生人数=二队女生人数+三队女生人数,一队女生占本队人数的:1-=;一队女生占总人数的×=,二、三队女生占总人数的:1÷2×(1-)=,然后再相加。
46.20
解:3-1=2(分钟)
4-1=3(分钟)
2×3=6(分钟)
60×(10-8)
=60×2
=120(分)
120÷6=20(次)。
故答案为:20。
北京地铁4号线每2分钟到达一次,14号线每3分钟到达一次,这两条线同时到达北京南站的间隔时间是2和3的最小公倍数,这两条线同时到达北京南站的次数=(10时-8时)×平均每小时的分钟数÷这两条线同时到达北京南站的间隔时间。
47.35
解:1升=1000毫升
(1000+10-800)÷(5+1)
=210÷6
=35(毫升)
35毫升=35立方厘米。
故答案为:35。
一个铁球的体积=(杯子的容积+溢出水的体积-倒入水的体积) ÷(先放入铁球的个数+又放入铁球的个数)。
48.4
解:20和12的最大公因数是2×2=4,则正方形纸的边长最大是4分米。
故答案为:4。
正方形纸的边长最大是20和12的最大公因数,可以用短除法求出。
49.;;0.75;1.25
解:1÷4=,7÷4=,3÷4=0.75,5÷4=1.25。
故答案为:;;0.75;1.25。
把单位“1”平均分成4份,每份是,几份就是几除以4。
50.;
解:5÷3=(千克)
1÷3=。
故答案为:;。
每个瓶子能装的质量=花生油的总质量÷平均装的瓶数;每个瓶子能装这桶花生油的分率=1÷平均装的瓶数。
同课章节目录
