高一上学期数学 人教A版2019必修第一册第一章 集合与常用逻辑用语 课件(共16张PPT)
文档属性
| 名称 | 高一上学期数学 人教A版2019必修第一册第一章 集合与常用逻辑用语 课件(共16张PPT) |

|
|
| 格式 | pptx | ||
| 文件大小 | 646.6KB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 人教A版(2019) | ||
| 科目 | 数学 | ||
| 更新时间 | 2025-05-30 11:35:14 | ||
图片预览





文档简介
(共16张PPT)
章末复习课
《集合与常用逻辑用语》
1.能够掌握集合的概念、元素与集合间的关系、集合与集合间的关系、集合的基本运算;
2.熟练地掌握集合的Venn图表示法和数轴表示法,培养数形结合思想;
3.能够利用命题之间的关系判定充要关系或进行充要条件的证明;
4.掌握全称命题与特称命题真假性的判定且能正确地对含有一个量词的命题进行否定.
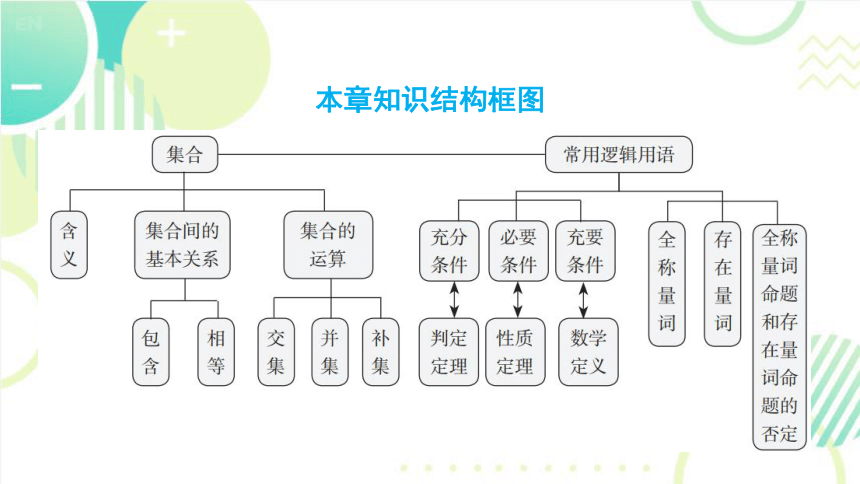
本章知识结构框图
为什么学习集合?
明确研究对象、确定研究范围是研究数学问题的基础;
把研究对象放在一起作为一个整体看待,就形成一个集合;
使用集合的语言和工具,可以简洁、准确地表述研究对象及研究范围;
集合语言是数学的基本语言,是现代数学的基础.
集合是刻画一类事物的语言和工具;
为什么学习逻辑用语?
使用常用逻辑用语表达数学对象、进行数学推理,可以提高交流的严谨性和准确性,提升逻辑推理素养;
逻辑用语是数学语言的重要组成部分,是数学表达和交流的工具,是逻辑思维的基本语言.
数学的重要特征是它的严谨性;
数学知识是建立在有限的定义和公理基础上的一系列数学推理;
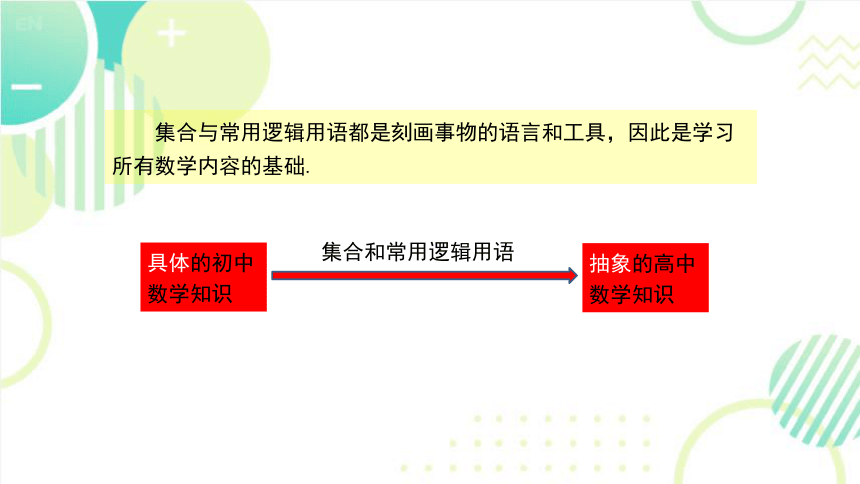
集合和常用逻辑用语
集合与常用逻辑用语都是刻画事物的语言和工具,因此是学习所有数学内容的基础.
具体的初中数学知识
抽象的高中数学知识
类型一、集合的概念与集合中的元素
解:
解:
类型一、集合的概念与集合中的元素
类型二、集合间的基本关系
解:
确定性
无序性
互异性
类型二、集合间的基本关系
空集是任意集合的子集
解:
类型三、集合的运算
解:(1)
(2)满足 需
显然无解,故不存在这样的
类型四、集合的应用
例5.学校举办运动会时,高一(1)班共有28名同学参加比赛,有15人参加游泳比赛,有8人参加田径比赛,有14人参加球类比赛,同时参加游泳比赛和田径比赛的有3人,同时参加游泳比赛和球类比赛的有3人,没有人同时参加三项比赛.同时参加田径和球类比赛的有多少人?只参加游泳一项比赛的有多少人?
解:
类型五、充分条件与必要条件
解:
类型六、全称量词与存在量词和两种命题的否定
类型六、全称量词与存在量词和两种命题的否定
1.本章所学内容包含了哪些知识点?你能自己画出知识结构图吗
2.解决集合问题需要注意什么呢?数轴和Venn图在解决集合问题中有什么作用呢?
3.类比数的运算,你还能定义集合其他的运算吗?能给出两个集合的减法运算吗?
4.你能从集合的角度分析充分条件、必要条件和充要条件及命题与命题的否定吗?
章末复习课
《集合与常用逻辑用语》
1.能够掌握集合的概念、元素与集合间的关系、集合与集合间的关系、集合的基本运算;
2.熟练地掌握集合的Venn图表示法和数轴表示法,培养数形结合思想;
3.能够利用命题之间的关系判定充要关系或进行充要条件的证明;
4.掌握全称命题与特称命题真假性的判定且能正确地对含有一个量词的命题进行否定.
本章知识结构框图
为什么学习集合?
明确研究对象、确定研究范围是研究数学问题的基础;
把研究对象放在一起作为一个整体看待,就形成一个集合;
使用集合的语言和工具,可以简洁、准确地表述研究对象及研究范围;
集合语言是数学的基本语言,是现代数学的基础.
集合是刻画一类事物的语言和工具;
为什么学习逻辑用语?
使用常用逻辑用语表达数学对象、进行数学推理,可以提高交流的严谨性和准确性,提升逻辑推理素养;
逻辑用语是数学语言的重要组成部分,是数学表达和交流的工具,是逻辑思维的基本语言.
数学的重要特征是它的严谨性;
数学知识是建立在有限的定义和公理基础上的一系列数学推理;
集合和常用逻辑用语
集合与常用逻辑用语都是刻画事物的语言和工具,因此是学习所有数学内容的基础.
具体的初中数学知识
抽象的高中数学知识
类型一、集合的概念与集合中的元素
解:
解:
类型一、集合的概念与集合中的元素
类型二、集合间的基本关系
解:
确定性
无序性
互异性
类型二、集合间的基本关系
空集是任意集合的子集
解:
类型三、集合的运算
解:(1)
(2)满足 需
显然无解,故不存在这样的
类型四、集合的应用
例5.学校举办运动会时,高一(1)班共有28名同学参加比赛,有15人参加游泳比赛,有8人参加田径比赛,有14人参加球类比赛,同时参加游泳比赛和田径比赛的有3人,同时参加游泳比赛和球类比赛的有3人,没有人同时参加三项比赛.同时参加田径和球类比赛的有多少人?只参加游泳一项比赛的有多少人?
解:
类型五、充分条件与必要条件
解:
类型六、全称量词与存在量词和两种命题的否定
类型六、全称量词与存在量词和两种命题的否定
1.本章所学内容包含了哪些知识点?你能自己画出知识结构图吗
2.解决集合问题需要注意什么呢?数轴和Venn图在解决集合问题中有什么作用呢?
3.类比数的运算,你还能定义集合其他的运算吗?能给出两个集合的减法运算吗?
4.你能从集合的角度分析充分条件、必要条件和充要条件及命题与命题的否定吗?
同课章节目录
- 第一章 集合与常用逻辑用语
- 1.1 集合的概念
- 1.2 集合间的基本关系
- 1.3 集合的基本运算
- 1.4 充分条件与必要条件
- 1.5 全称量词与存在量词
- 第二章 一元二次函数、方程和不等式
- 2.1 等式性质与不等式性质
- 2.2 基本不等式
- 2.3 二次函数与一元二次方程、不等式
- 第三章 函数概念与性质
- 3.1 函数的概念及其表示
- 3.2 函数的基本性质
- 3.3 幂函数
- 3.4 函数的应用(一)
- 第四章 指数函数与对数函数
- 4.1 指数
- 4.2 指数函数
- 4.3 对数
- 4.4 对数函数
- 4.5 函数的应用(二)
- 第五章 三角函数
- 5.1 任意角和弧度制
- 5.2 三角函数的概念
- 5.3 诱导公式
- 5.4 三角函数的图象与性质
- 5.5 三角恒等变换
- 5.6 函数 y=Asin( ωx + φ)
- 5.7 三角函数的应用
