中心对称图形复习2

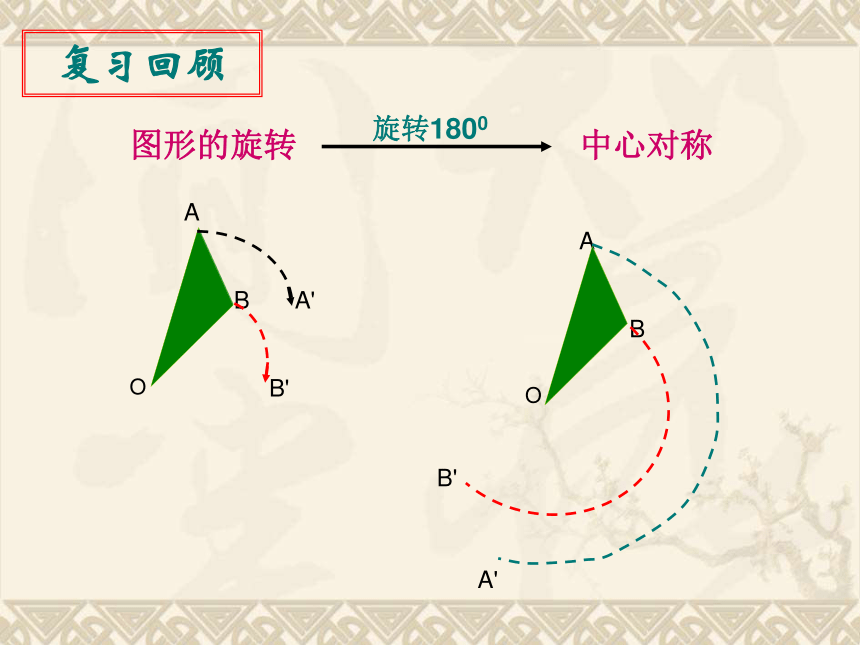
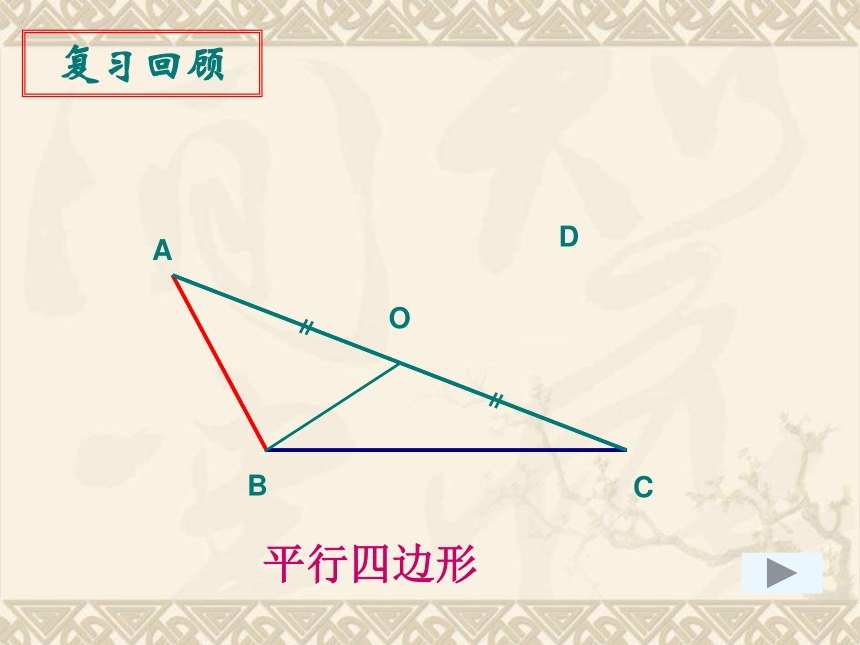
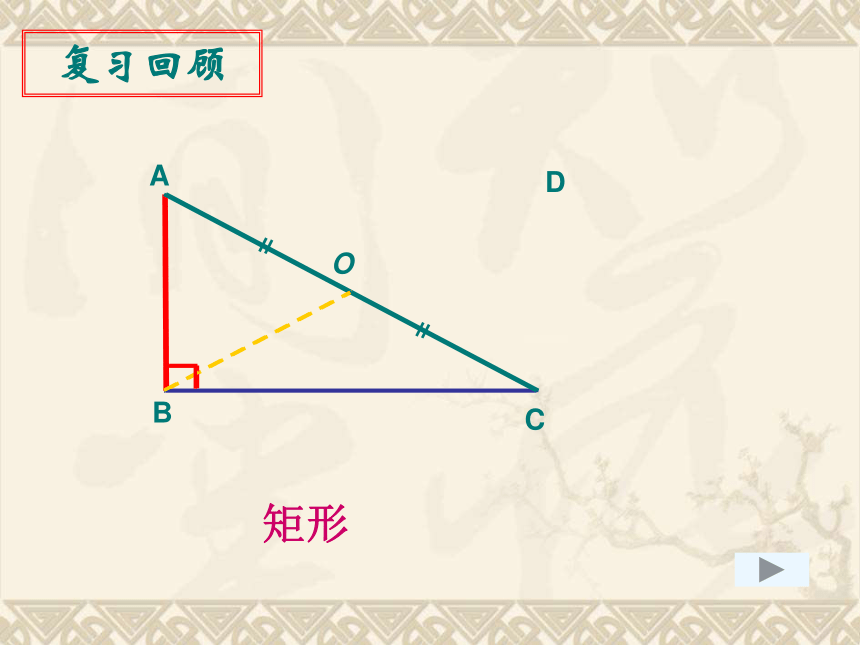
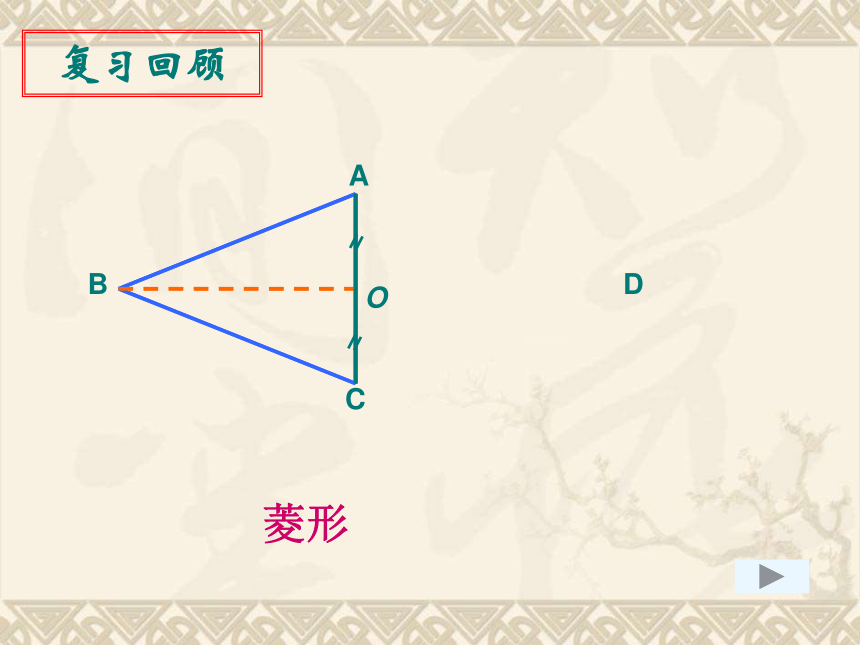
课件20张PPT。中心对称图形（一）复习课(1)A'B'BOA图形的旋转中心对称A'B'BOA复习回顾ABCOD平行四边形复习回顾ABCOD矩形复习回顾ABCDO菱形复习回顾ABCOD正方形复习回顾①平行四边形的对边平行；
②平行四边形的对边相等；
③平行四边形的对角相等；
④平行四边形的对角线互相平分。①2组对边分别平行的四边形是平行四边形；
②2组对边分别相等的四边形是平行四边形；
③一组对边平行且相等的四边形是平行四边形；
④对角线互相平分的四边形是平行四边形。
性质判定方法性质①矩形是特殊的平行四边形，它具有平行四边形的一切性质；
②矩形的四个角都是直角；
③矩形的对角线相等。判定方法①有一个角是直角的平行四边形是矩形；
②有3个角是直角的四边形是矩形；
③对角线相等的平行四边形是矩形。①菱形是特殊的平行四边形，它具有平行四边形的一切性质；
②菱形的四条边相等；
③菱形的对角线互相垂直，并且每一条对角线平分一组对角。性质判定方法①有一组邻边相等的平行四边形是菱形；
②四边都相等的四边形是菱形；
③对角线互相垂直的平行四边形是菱形。性质判定方法正方形具有矩形的性质，同时又具有菱形的
性质。
①有一组邻边相等并且有一个角是直角的平行
四边形是正方形
②有一组邻边相等的矩形是正方形；
③有一个角是直角的菱形是正方形。平行四边形、矩形、菱形、正方形之间的关系 1．矩形的两条对角线的夹角为600，较短的边长为12cm，
则对角线长为 cm.2．菱形的周长为20，一条对角线长为6，则另一条对角线长为 ，菱形的面积为 .3．如图，□ABCD的对角线AC、BD相交于点O，过点O的直线OM⊥AC．已知ΔCDM的周长是22㎝．则□ABCD的周长是 ㎝．
4．如图，正方形ABCD绕点A旋转后得到正方AB′C′D′
① 旋转角是 度
② 若AB=1，则C′ D= .
基础练习例1： 如图，平行四边形 ABCD的对角线AC的垂直平分线与边AD，BC分别交于点E，F．
试说明四边形AFCE是菱形．解：在□ ABCD中， AD//BC∴∠ EAO=∠ OCF, ∠ AEO=∠OFC
∵AO=CO
∴Δ AOE≌Δ COF∴OE=OF∴四边形AFCE是平行四边形∵EF⊥AC
∴四边形AFCE是菱形例题分析例2：如图，在梯形ABCD中，AD//BC，AB//DE，AF//DC，E，F两点在边BC上，且四边形AEFD是平行四边形．
（1）AD与BC有何等量关系？请说明理由；
（2）当AB=DC时，试说明□AEFD是矩形．解：理由如下：∴四边形ABED和四边形AFCD都是平行四边形.∵ AD//BC，AB//DE，AF//DC∴AD=BE，AD=CF∵四边形AEFD是平行四边形∴AD=EF∴AD=BE=EF=FC∴BC=3AD(1)BC=3AD(2) ∵四边形ABED和四边形AFCD都是平行四边形∴AB=DE，AF=DC∴DE=AF∵AB=DC又∵四边形AEFD是平行四边形∴四边形AEFD是矩形例3：如图，矩形ABCD中，AE平分∠BAD，交BC于E，对角线AC、BD交于O，若∠OAE＝15°。（1）试说明：OB＝BE；（2）求∠BOE的度数.解：（1）在矩形ABCD中，AE平分∠BAD∴ ∠BAE=45 °∴ ∠BAO=60 °∵∠OAE＝15°∵矩形ABCD中，OA=OB∴△OAB是等边三角形∴ AB=OB ∴AB=BE∴OB=BE（2）∵ △OAB是等边三角形∴ ∠ABO=60 °∴ ∠OBC=30 °∴ ∠BOE=75 °∵ OB=BE例4：如图，正方形ABCD，AC、BD相交于点O，点E在AC上，连接BE，作AG⊥BE，垂足为G，且交直线BD于F。
（1）试说明：OE＝OF；
（2）若点E在AC的延长线上，其余条件不变，（1）的结论还成立吗？画出图形，并说明理由。解：(1)在正方形ABCD中， AO=BO,∠AOF= ∠BOE=90 °∵ AG⊥BE∴ ∠AGB=90 °∵∠AFO=∠BFG∴ ∠OAF=∠OBE∴ △AOF≌△BOE∴ OE=OF(2)在正方形ABCD中， AO=BO,∠AOF= ∠BOE=90 °∵ AG⊥BE∴ ∠FGB=90 °∵∠OBE=∠GBF∴ ∠AFO=∠BEO∴ △AOF≌△BOE∴ OE=OF例4：如图，正方形ABCD，AC、BD相交于点O，点E在AC上，连接BE，作AG⊥BE，垂足为G，且交直线BD于F。
（1）试说明：OE＝OF；
（2）若点E在AC的延长线上，其余条件不变，（1）的结论还成立吗？画出图形，并说明理由。解：如图,直角梯形ABCD中，AD∥BC，AB⊥BC，
AD＝2，BC＝3，将腰CD以D为中心逆时针旋转90°至ED，连AE、CE，则△ADE的面积是( )
A．1 B．2 C．3 D．不能确定FG ?A通过本堂课的学习，
说说你的收获和体会祝同学们学习进步!