2025年北师大版小学数学五年级下册期末达标素养卷(含答案)
文档属性
| 名称 | 2025年北师大版小学数学五年级下册期末达标素养卷(含答案) |  | |
| 格式 | docx | ||
| 文件大小 | 470.8KB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 北师大版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2025-05-29 09:50:55 | ||
图片预览



文档简介
中小学教育资源及组卷应用平台
2025年北师大版小学数学五年级下册期末达标素养卷
一、填空题(共20分)
1.如图,从小刚家出发,向 °方向走 米到达广场,然后再从广场向 °方向走 米到达银行。
2.五位评委给一名参赛歌手打分,如果去掉一个最高分和一个最低分,平均分是9.25分,如果只去掉最低分平均分是9.35分,最高分是 分。
3.两辆汽车分别同时从两地出发,相向而行,t时相遇。两地相距 千米,相遇时小轿车比卡车多行了 千米。
4.建华小学五年级和六年级共种树204棵,六年级种树的棵数比五年级的2倍少36棵,五年级种树 棵,六年级种树 棵.(用方程解)
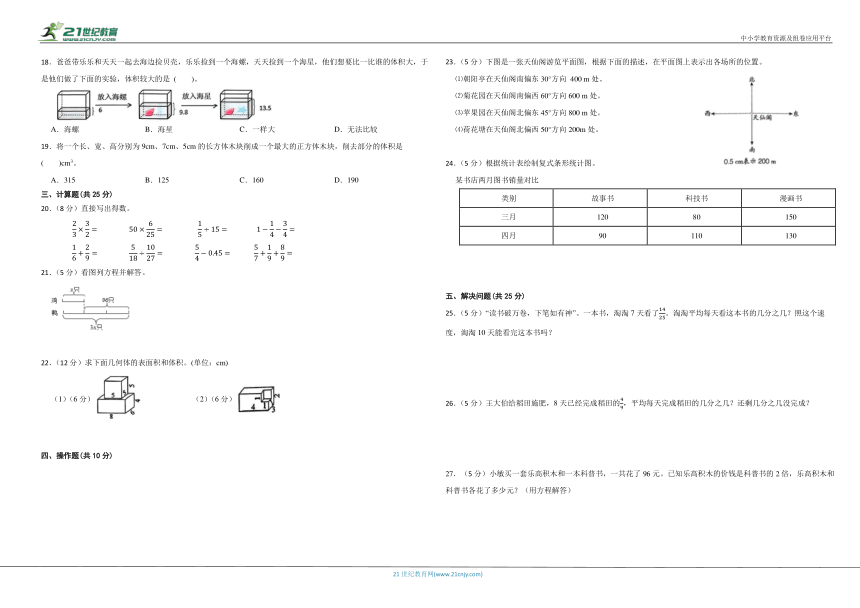
5.把一根 米长的绳子,平均剪成4段,其中每段占全长的 ,每段长 米。
6.古代女子的年龄称谓如下图所示。姐姐的年龄按古代的称谓是碧玉年华,妹妹的年龄按古代的称谓是金钗之年。妹妹的年龄是姐姐年龄的 。
7.在横线上填写合适的容积或体积单位。
一台微波炉容积约30 肥皂的体积约是150 一支口服液约10 衣柜的体积约是2
8.科学课上,同学们学习了很多金属的性质。有一个棱长为4dm的正方体金属,将它放入一个长8dm、宽5dm的长方体容器中(完全浸没在水中)。若原来容器中水面的高度是6dm,则放入金属后水面的高度是 dm。(水未溢出)
9.一个正方体的棱长之和是96厘米,这个正方体的棱长是 厘米,表面积是 厘米2,体积是 厘米3。
二、单选题(共20分)
10.笑笑上学时向南偏西45°方向行走了750米到学校,放学时应向( )方向就可以回家。
A.南偏西45°750米 B.北偏西45°250米 C.东偏北45°250米 D.北偏东45°750米
11.学校准备在4月18日举行五年级“三分钟定点投篮”比赛,每班派一名代表参加。五(1)班陈飞和张亮都想代表班级参加比赛,并认真地进行了练习。下图为他们4月11日—17日连续7天练习的成绩。派谁去参加比赛呢?
同学们推荐张亮参加比赛,下面哪些信息可以作为支持理由?( )
①在7天练习中,张亮的平均成绩比陈飞高。
②张亮在第7天投中了21个,陈飞这7天中没有出现过这样的好成绩。
③张亮的成绩一直在稳步上升,他比赛时有可能出现更好的成绩。
④陈飞的成绩上下波动比较明显。照这样,他比赛当天的成绩一定会比前一天低。
A.只有①③ B.只有②④ C.只有①②③ D.①②③④
12.甲、乙两列火车同时从两地相对出发,4小时后在离中点约10km的地方相遇。已知慢车每小时行50km,那么快车每小时行多少千米?设快车每小时行xkm,下列方程中,正确的是( )。
A.4x-50×4=10 B.4x-50×4=10×2 C.4x-10=50×4+10×2 D.4x-50×4=50+10
13.果园里有桃树、李树和荔枝树,李树比荔枝树的3倍多28棵,荔枝树比桃树少70棵,桃树和李树总和是荔枝树的6倍,这三种树共有( )棵。
A.303 B.323 C.343 D.363
14.下列算式,结果比1 小的是 ( )。
A. B. C. D.
15.妈妈的年龄比笑笑年龄的3倍多4岁,妈妈今年37岁,笑笑今年几岁?设笑笑今年x岁,根据其中的等量关系,下列方程正确的是( )。
A. B. C. D.
16.学校五年级有280人,六年级人数比五年级少 ,求六年级比五年级少多少人,列式为 ( )。
A.280-280× B.280× C.280+280× D.280-
17.下面情境图可以用 来解决的是 ( )。
A. B.
C. D.
18.爸爸带乐乐和天天一起去海边捡贝壳,乐乐捡到一个海螺,天天捡到一个海星,他们想要比一比谁的体积大,于是他们做了下面的实验,体积较大的是 ( )。
A.海螺 B.海星 C.一样大 D.无法比较
19.将一个长、宽、高分别为9cm、7cm、5cm的长方体木块削成一个最大的正方体木块,削去部分的体积是( )cm3。
A.315 B.125 C.160 D.190
三、计算题(共25分)
20.(8分)直接写出得数。
21.(5分)看图列方程并解答。
22.(12分)求下面几何体的表面积和体积。(单位:cm)
(1)(6分) (2)(6分)
四、操作题(共10分)
23.(5分)下图是一张天仙阁游览平面图,根据下面的描述,在平面图上表示出各场所的位置。
⑴朝阳亭在天仙阁南偏东30°方向 400 m处。
⑵菊花园在天仙阁南偏西60°方向600 m处。
⑶苹果园在天仙阁北偏东45°方向800 m处。
⑷荷花塘在天仙阁北偏西50°方向200m处。
24.(5分)根据统计表绘制复式条形统计图。
某书店两月图书销量对比
类别 故事书 科技书 漫画书
三月 120 80 150
四月 90 110 130
五、解决问题(共25分)
25.(5分)“读书破万卷,下笔如有神”。一本书,淘淘7天看了。淘淘平均每天看这本书的几分之几?照这个速度,淘淘10天能看完这本书吗?
26.(5分)王大伯给稻田施肥,8天已经完成稻田的,平均每天完成稻田的几分之几?还剩几分之几没完成?
(5分)小敏买一套乐高积木和一本科普书,一共花了96元。已知乐高积木的价钱是科普书的2倍,乐高积木和科普书各花了多少元?(用方程解答)
(5分)甲、乙两地相距900千米,一辆货车和一列客车分别同时从甲、乙两地相对开出,货车每时行80千米,客车每时行120千米,经过多少时两车在途中相遇?(用方程解)
29.(5分)“度量衡”是我国古代计量长度、容积、质量的标准或器具的统称。“度”用以计量长短;“量”用以测量容积大小;“衡”用以测量物体轻重。“商鞅变法”的重要物证————商鞅方升(如下图),就是“度量衡”中的“量”。它全长18.7厘米,内口长约12.5厘米、宽约7厘米、深约2.3厘米。它的容积便是商鞅规定的“一升”。算一算,商鞅规定的“一升”大约相当于现在的多少升?(得数保留一位小数)
答案解析部分
1.东偏北30;200;南偏东40;300
解:从小刚家出发,向东偏北30°方向走200米到达广场,然后再从广场向南偏东40°方向走300米到达银行。
故答案为:东偏北30;200;南偏东40;300。
在地图上的方位是上北,下南,左西,右东;东和西相对,南和北相对;西南和东北相对,西北和东南相对。描述路线图时,要先按行走路线确定每一个观测点,然后以每一个观测点为参照物,描述到下一个目标所行走的方向和路程。
2.9.65
解:9.25×3=27.75(分)
9.35×4=37.4(分)
37.4-27.75=9.65(分)。
故答案为:9.65。
最高分=只去掉最低分平均分×4-去掉一个最高分和一个最低分后的平均分×3。
3.110t;14t
解:(62+48)×t=110t(千米)
(62-48)×t=14t(千米)。
故答案为:110t;14t。
两地相距的路程=两辆汽车的速度和×相遇时间;相遇时小轿车比卡车多行的路程=(小轿车的速度-卡车的速度) ×相遇时间。
4.80;124
解:设五年级种树X棵,那么六年级种树(2X–36)棵。
X+2X–36=204
3X=240
X=80
2X–36=2x80–36=124
答:五年级种树80棵,六年级种树124棵。
故填:80;124
题意可知,五年级种树棵树是1倍量,“六年级种树棵树比五年级的2倍少36棵”是本题关键句,“五年级和六年级共种树204棵”是列方程的关系式。即五年级种树棵树+六年级种树棵树=共种树棵树。
5.;
解:把一根 米长的绳子,平均剪成4段,其中每段占全长的,每段长÷4=(米)。
故答案为:;。
把绳子的长度看作单位“1”,根据分数的意义确定每段占全长的几分之几。用绳子的长度除以剪成的段数即可求出每段的长度。
6.
解:12÷16=
故答案为:。
妹妹的年龄是12岁,姐姐的年龄是16岁。用妹妹的年龄除以姐姐的年龄即可求出妹妹的年龄是姐姐的几分之几。
7.L;cm3;mL;m3
解:一台微波炉容积约30L;
肥皂的体积约是150cm3;
一支口服液约10mL;
衣柜的体积约是2m3。
故答案为:L;cm3;mL;m3。
根据实际情况选择合适的单位,要注意联系生活经验、计量单位和数据的大小,多积累生活参照,灵活选择。
8.7.6
解:4×4×4÷(8×5)+6
=64÷40+6
=1.6+6
=7.6(dm)
故答案为:7.6。
通过实际操作可知:当正方体完全浸没在水中,且水未溢出时,正方体的体积等于上升部分水的体积,上升部分水的底面积等于容器的底面积,上升部分水的高等于水面上升的高度,因此,棱长×棱长×棱长=上升部分水的体积,长×宽=上升部分水的底面积,棱长×棱长×棱长÷(长×宽)=水面上升的高度,棱长×棱长×棱长÷(长×宽)+原水面高度=放入金属后水面的高度。
9.8;384;512
解:96÷12=8(厘米)
8×8×6
=64×6
=384(平方厘米)
8×8×8
=64×8
=512(立方厘米)
故答案为:8;384;512。
根据正方体的特征可知:正方体的棱长之和÷12=正方体的棱长,棱长×棱长×6=正方体的表面积,棱长×棱长×棱长=正方体的体积。
10.D
解:南和北相对,西和东相对,笑笑上学时向南偏西45°方向行走了750米到学校,放学时应向北偏东45°750米方向就可以回家。
故答案为:D。
两个位置是相对的,分别以它们为观察中心时,看到对方的方向相反,角度和距离相等。
11.C
解:①陈飞的平均成绩:
(11+12+15+14+19+16+19)÷7
=106÷7
≈15(个)
张亮的平均成绩:
(10+13+14+17+18+19+21)÷7
=112÷7
=16(个)
16>15,在七天练习中,张亮的平均成绩比陈飞高,原题说法正确;
②在七天中,张亮的最好成绩出现在第七天,是21个;陈飞的最好成绩出现在第五天和第七天,是19个,低于张亮的最好成绩,原题说法正确;
③表示陈飞成绩的折线,是忽高忽低的走势,说明他的成绩有波动;而表示张亮成绩的折线,一直呈上升的趋势,说明一直在稳步上升,他比赛时有可能出现更好的成绩,原题说法正确;
④尽管陈飞的成绩上下波动比较明显,但不代表比赛当天成绩一定会比前一天低,比赛当天的成绩是不确定的,原题说法错误。
可以作为支持理由的有①②③。
故答案为:C。
①平均数的计算是用所有数据的和除以需要分的总次数后所得的商;可分别计算出两人七天练均成绩,再比较即可;
②观察两人在七天中,最好的成绩分别是多少,再加以比较;
③折线的上升、下降,能够表示出两人成绩的上升和下降,分别观察表示两人成绩的折线的走势,再做判断即可;
④结合统计图的走势可以观察到两人成绩的变化情况,但是之前的成绩波动,并不能代表之后成绩一定会波动。据此解答。
12.B
解:设快车每小时行x千米。可以列方程4x-50×4=10×2。
故答案为:B。
设快车每小时行x千米。依据等量关系式:快车的速度×行驶时间-慢车的速度×行驶时间=离中点的距离×2,列方程。
13.C
解: 设荔枝树有 x 棵,李树有(3 x + 28)棵,桃树有(x + 70)棵。
( 3 x + 28 ) + ( x + 70 ) = 6 x
4 x + 98 = 6 x
98 = 2 x
x = 49
李树:3 × 49 + 28 = 175(棵)
桃树:49 + 70 = 119 (棵)
三种树共有:49 + 175 + 119 = 343(棵)。
故答案为:C。
设荔枝树有 x 棵,李树有(3 x + 28)棵,桃树有(x + 70)棵。依据等量关系式: 桃树和李树的总和是荔枝树的6倍,列方程,解方程,求出荔枝树有49棵,分别求出其余两种的棵数,再相加。
14.A
解:选项A,-=,<1;
选项B,+=,>1;
选项C,6×=,>1;
选项D,÷=,>1。
故答案为:A。
异分母分数加减法计算方法:先通分,然后按照同分母分数加减法的法则进行计算,计算结果能约分的要约成最简分数,据此计算,再比较与1的大小。
15.C
解:设笑笑今年x岁,3x+4=37。
故答案为:C。
设笑笑今年x岁,依据等量关系式:笑笑今年的年龄×3+多的岁数=妈妈今年的岁数,列方程。
16.B
解:280×
故答案为:B。
根据题意可知把五年级人数看作单位“1”,五年级人数×六年级比五年级少的分率=六年级比五年级少的人数,据此可以判断。
17.D
解:A:+,不符合题意;
B:-,不符合题意;
C:2+1,不符合题意;
D:×,符合题意。
故答案为:D。
A:看图可知是求吨与吨的和是多少吨,用加法;
B:看图可知是求米比米长多少米,用减法;
C:看图可知是把一个黑圆并给两个白圆,因此用加法;
D:看图可知是求的是多少,求一个数的几分之几是多少,用乘法。
18.A
解:9.8-6=3.8
13.5-9.8=3.7
3.8>3.7,即海螺的体积比海星的体积大。
故答案为:A。
通过实际操作可知应用排水法测量不规则物体体积时,当不规则物体完全浸没在水中时上升部分水的体积等于不规则物体的体积,上升部分水的底面积等于容器的底面积,上升部分水的高等于水面上升的高度,因此,根据题意可知测量海螺与海星时容器是同一个即它们的底面积是相等的,所以只需比较水面上升的高度即可判断:放入海螺时的水面高度-原水面高度=放入海螺后水面上升高度,放入海星后水面高度-放入海螺后水面高度=放入海星后水面上升高度,最后比较两个水面上升高度即可判断。
19.D
解:9×7×5
=63×5
=315(立方厘米)
315-5×5×5
=315-125
=190(立方厘米)
故答案为:D。
根据正方体的特征12条棱一样长可知把一个长方体削成一个最大的正方体,则正方体的棱长只能是长方体中最短的那条棱即5cm,因此,长×宽×高=长方体的体积,棱长×棱长×棱长=正方体的体积,长方体的体积-棱长×棱长×棱长=削去部分的体积。
20.
1 12 0
0.8
异分母分数加减法计算方法: 先通分,然后按照同分母分数加减法的法则进行计算;
分数乘法的计算法则:分数乘分数,用分子相乘的积作分子,分母相乘的积作分母;
分数除法的计算法则: 甲数除以乙数(0除外),等于甲数乘乙数的倒数,据此解答。
21.解:3x-x=96
2x=96
x=96÷2
x=48
3x=3×48=144
答:鸡有48只,鸭有144只。
依据等量关系式:鸭的只数-鸡的只数=96只,列方程,解方程。
22.(1)解:表面积
5×5×4+(8×6+8×4+6×4)×2
=100+104×2
=100+208
=308(cm2)
体积
5×5×5+8×6×4
=125+192
=317(cm3)
(2)解:表面积
(4×3+4×2+3×2)×2
=26×2
=52(cm2)
体积
4×3×2-1×1×1
=24-1
=23(cm3)
(1)把正方体的上面平移到下面,则长方体的表面积就是完整6个面的面积和,此时正方体的表面积就是4个面的面积和,因此,棱长×棱长×4=正方体的表面积,(长×宽+长×高+宽×高)×2=长方体的表面积,棱长×棱长×4+(长×宽+长×高+宽×高)×2=几何体的表面积;棱长×棱长×棱长=正方体的体积,长×宽×高=长方体的体积,棱长×棱长×棱长+长×宽×高=几何体的体积;
(2)把凹进去的三个面分别平移到它们的对面,则几何体的表面积就是长方体的表面积,因此,(长×宽+长×高+宽×高)×2=几何体的表面积;棱长×棱长×棱长=正方体的体积,长×宽×高=长方体的体积,长×宽×高-棱长×棱长×棱长=几何体的体积。
23.解:(1)
(2)
(3)
(4)
图上的方向是上北下南、左西右东,图上0.5cm表示200m,根据实际情况确定图上距离,根据图上的方向、夹角度数和图上距离分别确定每个点的位置即可。
24.解:
绘制复式条形统计图,用直条的长度表示数据的多少,由于数据均为十几,要用一格表示20个单位,可以用横轴表示月份,纵轴表示图书销量,依据图例中不同的直条高度表示图书的类别,依据统计表中的数据画出直条,并且标上数据。
25.解: ÷7=
1÷=12.5(天)
12.5>10
答: 淘淘平均每天看这本书的,照这个速度,淘淘10天不能看完这本书。
要求淘淘每天看书的进度,用他7天看的书的分率除以7来计算。接下来,把这本书的总页数看作单位“1”,然后除以 淘淘平均每天看这本书的 分率即可。
26.解: ÷8=
1-=
答: 平均每天完成稻田的,还剩没完成。
根据8天完成稻田的 ,求平均每天完成稻田的几分之几,求平均数,用 除以8;求还剩几分之几,用单位“1”减去 ,据此解答。
27.解:设科普书的价钱是x元,则乐高积木的价钱是2x元。
x+2x=96
3x=96
x=96÷3
x=32
32×2=64(元)
答:科普书32元,乐高积木64元。
设科普书的价钱是x元,则乐高积木的价钱是2x元。依据科普书的价钱+乐高积木的价钱=总钱数,列方程,解方程。
28.解:设经过x小时两车在途中相遇。
(80+120)x=900
200x=900
x=900÷200
x=4.5
答:经过4.5小时两车在途中相遇。
设经过x小时两车在途中相遇。 依据等量关系式:(货车的速度+客车的速度)×相遇时间=甲、乙两地的路程,列方程,解方程。
29.解:12.5×7×2.3
=87.5×2.3
=201.25(立方厘米)
1升=1000毫升=1000立方厘米
201.25÷1000=0.201250.2(升)
答:商鞅规定的“一升”大约相当于现在的0.2升。
根据题意可得:内口长×宽×深=商鞅方升的体积,先统一单位:1升=1000毫升=1000立方厘米,再根据:商鞅方升的体积÷1000立方厘米=相当于多少升,结果再根据要求保留小数即可。
21世纪教育网(www.21cnjy.com)
2025年北师大版小学数学五年级下册期末达标素养卷
一、填空题(共20分)
1.如图,从小刚家出发,向 °方向走 米到达广场,然后再从广场向 °方向走 米到达银行。
2.五位评委给一名参赛歌手打分,如果去掉一个最高分和一个最低分,平均分是9.25分,如果只去掉最低分平均分是9.35分,最高分是 分。
3.两辆汽车分别同时从两地出发,相向而行,t时相遇。两地相距 千米,相遇时小轿车比卡车多行了 千米。
4.建华小学五年级和六年级共种树204棵,六年级种树的棵数比五年级的2倍少36棵,五年级种树 棵,六年级种树 棵.(用方程解)
5.把一根 米长的绳子,平均剪成4段,其中每段占全长的 ,每段长 米。
6.古代女子的年龄称谓如下图所示。姐姐的年龄按古代的称谓是碧玉年华,妹妹的年龄按古代的称谓是金钗之年。妹妹的年龄是姐姐年龄的 。
7.在横线上填写合适的容积或体积单位。
一台微波炉容积约30 肥皂的体积约是150 一支口服液约10 衣柜的体积约是2
8.科学课上,同学们学习了很多金属的性质。有一个棱长为4dm的正方体金属,将它放入一个长8dm、宽5dm的长方体容器中(完全浸没在水中)。若原来容器中水面的高度是6dm,则放入金属后水面的高度是 dm。(水未溢出)
9.一个正方体的棱长之和是96厘米,这个正方体的棱长是 厘米,表面积是 厘米2,体积是 厘米3。
二、单选题(共20分)
10.笑笑上学时向南偏西45°方向行走了750米到学校,放学时应向( )方向就可以回家。
A.南偏西45°750米 B.北偏西45°250米 C.东偏北45°250米 D.北偏东45°750米
11.学校准备在4月18日举行五年级“三分钟定点投篮”比赛,每班派一名代表参加。五(1)班陈飞和张亮都想代表班级参加比赛,并认真地进行了练习。下图为他们4月11日—17日连续7天练习的成绩。派谁去参加比赛呢?
同学们推荐张亮参加比赛,下面哪些信息可以作为支持理由?( )
①在7天练习中,张亮的平均成绩比陈飞高。
②张亮在第7天投中了21个,陈飞这7天中没有出现过这样的好成绩。
③张亮的成绩一直在稳步上升,他比赛时有可能出现更好的成绩。
④陈飞的成绩上下波动比较明显。照这样,他比赛当天的成绩一定会比前一天低。
A.只有①③ B.只有②④ C.只有①②③ D.①②③④
12.甲、乙两列火车同时从两地相对出发,4小时后在离中点约10km的地方相遇。已知慢车每小时行50km,那么快车每小时行多少千米?设快车每小时行xkm,下列方程中,正确的是( )。
A.4x-50×4=10 B.4x-50×4=10×2 C.4x-10=50×4+10×2 D.4x-50×4=50+10
13.果园里有桃树、李树和荔枝树,李树比荔枝树的3倍多28棵,荔枝树比桃树少70棵,桃树和李树总和是荔枝树的6倍,这三种树共有( )棵。
A.303 B.323 C.343 D.363
14.下列算式,结果比1 小的是 ( )。
A. B. C. D.
15.妈妈的年龄比笑笑年龄的3倍多4岁,妈妈今年37岁,笑笑今年几岁?设笑笑今年x岁,根据其中的等量关系,下列方程正确的是( )。
A. B. C. D.
16.学校五年级有280人,六年级人数比五年级少 ,求六年级比五年级少多少人,列式为 ( )。
A.280-280× B.280× C.280+280× D.280-
17.下面情境图可以用 来解决的是 ( )。
A. B.
C. D.
18.爸爸带乐乐和天天一起去海边捡贝壳,乐乐捡到一个海螺,天天捡到一个海星,他们想要比一比谁的体积大,于是他们做了下面的实验,体积较大的是 ( )。
A.海螺 B.海星 C.一样大 D.无法比较
19.将一个长、宽、高分别为9cm、7cm、5cm的长方体木块削成一个最大的正方体木块,削去部分的体积是( )cm3。
A.315 B.125 C.160 D.190
三、计算题(共25分)
20.(8分)直接写出得数。
21.(5分)看图列方程并解答。
22.(12分)求下面几何体的表面积和体积。(单位:cm)
(1)(6分) (2)(6分)
四、操作题(共10分)
23.(5分)下图是一张天仙阁游览平面图,根据下面的描述,在平面图上表示出各场所的位置。
⑴朝阳亭在天仙阁南偏东30°方向 400 m处。
⑵菊花园在天仙阁南偏西60°方向600 m处。
⑶苹果园在天仙阁北偏东45°方向800 m处。
⑷荷花塘在天仙阁北偏西50°方向200m处。
24.(5分)根据统计表绘制复式条形统计图。
某书店两月图书销量对比
类别 故事书 科技书 漫画书
三月 120 80 150
四月 90 110 130
五、解决问题(共25分)
25.(5分)“读书破万卷,下笔如有神”。一本书,淘淘7天看了。淘淘平均每天看这本书的几分之几?照这个速度,淘淘10天能看完这本书吗?
26.(5分)王大伯给稻田施肥,8天已经完成稻田的,平均每天完成稻田的几分之几?还剩几分之几没完成?
(5分)小敏买一套乐高积木和一本科普书,一共花了96元。已知乐高积木的价钱是科普书的2倍,乐高积木和科普书各花了多少元?(用方程解答)
(5分)甲、乙两地相距900千米,一辆货车和一列客车分别同时从甲、乙两地相对开出,货车每时行80千米,客车每时行120千米,经过多少时两车在途中相遇?(用方程解)
29.(5分)“度量衡”是我国古代计量长度、容积、质量的标准或器具的统称。“度”用以计量长短;“量”用以测量容积大小;“衡”用以测量物体轻重。“商鞅变法”的重要物证————商鞅方升(如下图),就是“度量衡”中的“量”。它全长18.7厘米,内口长约12.5厘米、宽约7厘米、深约2.3厘米。它的容积便是商鞅规定的“一升”。算一算,商鞅规定的“一升”大约相当于现在的多少升?(得数保留一位小数)
答案解析部分
1.东偏北30;200;南偏东40;300
解:从小刚家出发,向东偏北30°方向走200米到达广场,然后再从广场向南偏东40°方向走300米到达银行。
故答案为:东偏北30;200;南偏东40;300。
在地图上的方位是上北,下南,左西,右东;东和西相对,南和北相对;西南和东北相对,西北和东南相对。描述路线图时,要先按行走路线确定每一个观测点,然后以每一个观测点为参照物,描述到下一个目标所行走的方向和路程。
2.9.65
解:9.25×3=27.75(分)
9.35×4=37.4(分)
37.4-27.75=9.65(分)。
故答案为:9.65。
最高分=只去掉最低分平均分×4-去掉一个最高分和一个最低分后的平均分×3。
3.110t;14t
解:(62+48)×t=110t(千米)
(62-48)×t=14t(千米)。
故答案为:110t;14t。
两地相距的路程=两辆汽车的速度和×相遇时间;相遇时小轿车比卡车多行的路程=(小轿车的速度-卡车的速度) ×相遇时间。
4.80;124
解:设五年级种树X棵,那么六年级种树(2X–36)棵。
X+2X–36=204
3X=240
X=80
2X–36=2x80–36=124
答:五年级种树80棵,六年级种树124棵。
故填:80;124
题意可知,五年级种树棵树是1倍量,“六年级种树棵树比五年级的2倍少36棵”是本题关键句,“五年级和六年级共种树204棵”是列方程的关系式。即五年级种树棵树+六年级种树棵树=共种树棵树。
5.;
解:把一根 米长的绳子,平均剪成4段,其中每段占全长的,每段长÷4=(米)。
故答案为:;。
把绳子的长度看作单位“1”,根据分数的意义确定每段占全长的几分之几。用绳子的长度除以剪成的段数即可求出每段的长度。
6.
解:12÷16=
故答案为:。
妹妹的年龄是12岁,姐姐的年龄是16岁。用妹妹的年龄除以姐姐的年龄即可求出妹妹的年龄是姐姐的几分之几。
7.L;cm3;mL;m3
解:一台微波炉容积约30L;
肥皂的体积约是150cm3;
一支口服液约10mL;
衣柜的体积约是2m3。
故答案为:L;cm3;mL;m3。
根据实际情况选择合适的单位,要注意联系生活经验、计量单位和数据的大小,多积累生活参照,灵活选择。
8.7.6
解:4×4×4÷(8×5)+6
=64÷40+6
=1.6+6
=7.6(dm)
故答案为:7.6。
通过实际操作可知:当正方体完全浸没在水中,且水未溢出时,正方体的体积等于上升部分水的体积,上升部分水的底面积等于容器的底面积,上升部分水的高等于水面上升的高度,因此,棱长×棱长×棱长=上升部分水的体积,长×宽=上升部分水的底面积,棱长×棱长×棱长÷(长×宽)=水面上升的高度,棱长×棱长×棱长÷(长×宽)+原水面高度=放入金属后水面的高度。
9.8;384;512
解:96÷12=8(厘米)
8×8×6
=64×6
=384(平方厘米)
8×8×8
=64×8
=512(立方厘米)
故答案为:8;384;512。
根据正方体的特征可知:正方体的棱长之和÷12=正方体的棱长,棱长×棱长×6=正方体的表面积,棱长×棱长×棱长=正方体的体积。
10.D
解:南和北相对,西和东相对,笑笑上学时向南偏西45°方向行走了750米到学校,放学时应向北偏东45°750米方向就可以回家。
故答案为:D。
两个位置是相对的,分别以它们为观察中心时,看到对方的方向相反,角度和距离相等。
11.C
解:①陈飞的平均成绩:
(11+12+15+14+19+16+19)÷7
=106÷7
≈15(个)
张亮的平均成绩:
(10+13+14+17+18+19+21)÷7
=112÷7
=16(个)
16>15,在七天练习中,张亮的平均成绩比陈飞高,原题说法正确;
②在七天中,张亮的最好成绩出现在第七天,是21个;陈飞的最好成绩出现在第五天和第七天,是19个,低于张亮的最好成绩,原题说法正确;
③表示陈飞成绩的折线,是忽高忽低的走势,说明他的成绩有波动;而表示张亮成绩的折线,一直呈上升的趋势,说明一直在稳步上升,他比赛时有可能出现更好的成绩,原题说法正确;
④尽管陈飞的成绩上下波动比较明显,但不代表比赛当天成绩一定会比前一天低,比赛当天的成绩是不确定的,原题说法错误。
可以作为支持理由的有①②③。
故答案为:C。
①平均数的计算是用所有数据的和除以需要分的总次数后所得的商;可分别计算出两人七天练均成绩,再比较即可;
②观察两人在七天中,最好的成绩分别是多少,再加以比较;
③折线的上升、下降,能够表示出两人成绩的上升和下降,分别观察表示两人成绩的折线的走势,再做判断即可;
④结合统计图的走势可以观察到两人成绩的变化情况,但是之前的成绩波动,并不能代表之后成绩一定会波动。据此解答。
12.B
解:设快车每小时行x千米。可以列方程4x-50×4=10×2。
故答案为:B。
设快车每小时行x千米。依据等量关系式:快车的速度×行驶时间-慢车的速度×行驶时间=离中点的距离×2,列方程。
13.C
解: 设荔枝树有 x 棵,李树有(3 x + 28)棵,桃树有(x + 70)棵。
( 3 x + 28 ) + ( x + 70 ) = 6 x
4 x + 98 = 6 x
98 = 2 x
x = 49
李树:3 × 49 + 28 = 175(棵)
桃树:49 + 70 = 119 (棵)
三种树共有:49 + 175 + 119 = 343(棵)。
故答案为:C。
设荔枝树有 x 棵,李树有(3 x + 28)棵,桃树有(x + 70)棵。依据等量关系式: 桃树和李树的总和是荔枝树的6倍,列方程,解方程,求出荔枝树有49棵,分别求出其余两种的棵数,再相加。
14.A
解:选项A,-=,<1;
选项B,+=,>1;
选项C,6×=,>1;
选项D,÷=,>1。
故答案为:A。
异分母分数加减法计算方法:先通分,然后按照同分母分数加减法的法则进行计算,计算结果能约分的要约成最简分数,据此计算,再比较与1的大小。
15.C
解:设笑笑今年x岁,3x+4=37。
故答案为:C。
设笑笑今年x岁,依据等量关系式:笑笑今年的年龄×3+多的岁数=妈妈今年的岁数,列方程。
16.B
解:280×
故答案为:B。
根据题意可知把五年级人数看作单位“1”,五年级人数×六年级比五年级少的分率=六年级比五年级少的人数,据此可以判断。
17.D
解:A:+,不符合题意;
B:-,不符合题意;
C:2+1,不符合题意;
D:×,符合题意。
故答案为:D。
A:看图可知是求吨与吨的和是多少吨,用加法;
B:看图可知是求米比米长多少米,用减法;
C:看图可知是把一个黑圆并给两个白圆,因此用加法;
D:看图可知是求的是多少,求一个数的几分之几是多少,用乘法。
18.A
解:9.8-6=3.8
13.5-9.8=3.7
3.8>3.7,即海螺的体积比海星的体积大。
故答案为:A。
通过实际操作可知应用排水法测量不规则物体体积时,当不规则物体完全浸没在水中时上升部分水的体积等于不规则物体的体积,上升部分水的底面积等于容器的底面积,上升部分水的高等于水面上升的高度,因此,根据题意可知测量海螺与海星时容器是同一个即它们的底面积是相等的,所以只需比较水面上升的高度即可判断:放入海螺时的水面高度-原水面高度=放入海螺后水面上升高度,放入海星后水面高度-放入海螺后水面高度=放入海星后水面上升高度,最后比较两个水面上升高度即可判断。
19.D
解:9×7×5
=63×5
=315(立方厘米)
315-5×5×5
=315-125
=190(立方厘米)
故答案为:D。
根据正方体的特征12条棱一样长可知把一个长方体削成一个最大的正方体,则正方体的棱长只能是长方体中最短的那条棱即5cm,因此,长×宽×高=长方体的体积,棱长×棱长×棱长=正方体的体积,长方体的体积-棱长×棱长×棱长=削去部分的体积。
20.
1 12 0
0.8
异分母分数加减法计算方法: 先通分,然后按照同分母分数加减法的法则进行计算;
分数乘法的计算法则:分数乘分数,用分子相乘的积作分子,分母相乘的积作分母;
分数除法的计算法则: 甲数除以乙数(0除外),等于甲数乘乙数的倒数,据此解答。
21.解:3x-x=96
2x=96
x=96÷2
x=48
3x=3×48=144
答:鸡有48只,鸭有144只。
依据等量关系式:鸭的只数-鸡的只数=96只,列方程,解方程。
22.(1)解:表面积
5×5×4+(8×6+8×4+6×4)×2
=100+104×2
=100+208
=308(cm2)
体积
5×5×5+8×6×4
=125+192
=317(cm3)
(2)解:表面积
(4×3+4×2+3×2)×2
=26×2
=52(cm2)
体积
4×3×2-1×1×1
=24-1
=23(cm3)
(1)把正方体的上面平移到下面,则长方体的表面积就是完整6个面的面积和,此时正方体的表面积就是4个面的面积和,因此,棱长×棱长×4=正方体的表面积,(长×宽+长×高+宽×高)×2=长方体的表面积,棱长×棱长×4+(长×宽+长×高+宽×高)×2=几何体的表面积;棱长×棱长×棱长=正方体的体积,长×宽×高=长方体的体积,棱长×棱长×棱长+长×宽×高=几何体的体积;
(2)把凹进去的三个面分别平移到它们的对面,则几何体的表面积就是长方体的表面积,因此,(长×宽+长×高+宽×高)×2=几何体的表面积;棱长×棱长×棱长=正方体的体积,长×宽×高=长方体的体积,长×宽×高-棱长×棱长×棱长=几何体的体积。
23.解:(1)
(2)
(3)
(4)
图上的方向是上北下南、左西右东,图上0.5cm表示200m,根据实际情况确定图上距离,根据图上的方向、夹角度数和图上距离分别确定每个点的位置即可。
24.解:
绘制复式条形统计图,用直条的长度表示数据的多少,由于数据均为十几,要用一格表示20个单位,可以用横轴表示月份,纵轴表示图书销量,依据图例中不同的直条高度表示图书的类别,依据统计表中的数据画出直条,并且标上数据。
25.解: ÷7=
1÷=12.5(天)
12.5>10
答: 淘淘平均每天看这本书的,照这个速度,淘淘10天不能看完这本书。
要求淘淘每天看书的进度,用他7天看的书的分率除以7来计算。接下来,把这本书的总页数看作单位“1”,然后除以 淘淘平均每天看这本书的 分率即可。
26.解: ÷8=
1-=
答: 平均每天完成稻田的,还剩没完成。
根据8天完成稻田的 ,求平均每天完成稻田的几分之几,求平均数,用 除以8;求还剩几分之几,用单位“1”减去 ,据此解答。
27.解:设科普书的价钱是x元,则乐高积木的价钱是2x元。
x+2x=96
3x=96
x=96÷3
x=32
32×2=64(元)
答:科普书32元,乐高积木64元。
设科普书的价钱是x元,则乐高积木的价钱是2x元。依据科普书的价钱+乐高积木的价钱=总钱数,列方程,解方程。
28.解:设经过x小时两车在途中相遇。
(80+120)x=900
200x=900
x=900÷200
x=4.5
答:经过4.5小时两车在途中相遇。
设经过x小时两车在途中相遇。 依据等量关系式:(货车的速度+客车的速度)×相遇时间=甲、乙两地的路程,列方程,解方程。
29.解:12.5×7×2.3
=87.5×2.3
=201.25(立方厘米)
1升=1000毫升=1000立方厘米
201.25÷1000=0.201250.2(升)
答:商鞅规定的“一升”大约相当于现在的0.2升。
根据题意可得:内口长×宽×深=商鞅方升的体积,先统一单位:1升=1000毫升=1000立方厘米,再根据:商鞅方升的体积÷1000立方厘米=相当于多少升,结果再根据要求保留小数即可。
21世纪教育网(www.21cnjy.com)
同课章节目录
