2025年浙江省中考数学模拟试卷(9)(含解析)
文档属性
| 名称 | 2025年浙江省中考数学模拟试卷(9)(含解析) |  | |
| 格式 | doc | ||
| 文件大小 | 1.3MB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 浙教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2025-05-29 10:41:46 | ||
图片预览



文档简介
中小学教育资源及组卷应用平台
2025年浙江省中考数学模拟试卷(9)
一、选择题:本题共10小题,每小题3分,共30分。在每小题给出的四个选项中,只有一项是符合题目要求的。
1.(2025 渝北区一模)的相反数是( )
A. B. C.﹣ D.﹣
2.(2025 鹤山市一模)垃圾分类功在当代利在千秋,下列垃圾分类指引标志图形中,是轴对称图形又是中心对称图形的是( )
A.厨余垃圾Food Waste B.可回收物Recyclable
C.其他垃圾Residual Waste D.有害垃圾Hazardous Waste
3.(2024秋 娄底校级期末)电影《志愿军:存亡之战》以7.61亿元票房领跑2024年国庆档电影票房.其中数据7.61亿用科学记数法表示为( )
A.0.761×109 B.7.61×108 C.7.61×106 D.761×108
4.(2025 华蓥市模拟)下列计算正确的是( )
A.(m3)5=m15 B.m4+m4=m8 C.m6÷m2=m3 D.(m+1)2=m2+1
5.(2025 盐城一模)若点A(﹣3,y1),B(﹣1,y2),C(2,y3)在反比例函数的图象上,则y1,y2,y3的大小关系是( )
A.y1<y2<y3 B.y2<y1<y3 C.y3<y2<y1 D.y2<y3<y1
6.(2025 吉林二模)关于x的不等式2x﹣a≤﹣1的解集如图所示,那么a的值是( )
A.﹣2 B.2 C.﹣3 D.3
7.(2025 崂山区一模)某中学足球队16名队员的年龄情况如下表,则这些队员年龄的众数和中位数分别为( )
年龄(单位岁) 14 15 16 17 18
人数 2 4 5 3 2
A.15,16 B.16,16.5 C.16,16 D.17,16.5
8.(2025 西宁一模)某环卫公司为清理卫生死角内的垃圾,调用甲车3h,只清理了一半垃圾,为了加快进步,再调用乙车,两车合作1.2h清理完另一半垃圾,设乙车单独清理全部垃圾的时间为xh,根据题意可列出方程为( )
A.+=1 B.+= C.+=1 D.+=
9.(2025 义乌市二模)如图,在四边形ABCD中,已知AD∥BC,∠B=90°,,对角线AC平分∠BAD,∠DCA:∠BCA=2:3,则CD的值为( )
A. B. C. D.
10.(2025 滨江区一模)如图,AB,CD是⊙O的直径,AB⊥CD,点E为劣弧(不含端点)上一点,连接AE,CE,分别交OD,OB于点F,G.若⊙O的半径为1,记OF=x,BG=y,则下列代数式的值不变的是( )
A.2x﹣y B. C.2y﹣x D.
二、填空题:本题共6小题,每小题3分,共18分。
11.(2024 新丰县一模)因式分解:m2﹣25= .
12.(2025 上虞区二模)若分式的值为1,则字母x的取值为 .
13.(2025 濠江区一模)一个袋子中有2个白球和若干个黑球,它们除了颜色外都相同,随机从中摸一个球,恰好摸到黑球的概率是,则袋子中有 个黑球.
14.(2025 建邺区一模)如图,在矩形ABCD中,点A的坐标是(0,﹣1),点B的坐标是(2,0),点C在y轴上.若反比例函数的图象经过点D,则k= .
15.(2025 济宁二模)如图,⊙O半径为,正方形ABCD内接于⊙O,点E在上运动,连接BE,作AF⊥BE,垂足为F,连接CF.则CF长的最小值为 .
16.(2025 宣城二模)如图,正方形ABCD的边长为6,点E,F分别在BC,AD上.将该正方形沿EF折叠,使点A落在CD边上的点M处,连接AM,与折痕EF交于点P.
(1)若M是CD的中点,则AF的长为 ;
(2)若G为MN的中点,随着折痕EF位置的变化,PG+PM的最小值为 .
三.解答题(共8小题,其中第17-22题每题8分,第23题10分,第24题每题12分,共72分)
17.(2025 西宁一模)计算:.
18.(2025 乾安县模拟)先化简,再求值:(2a+b)2﹣(b﹣2a)(2a+b),其中a=﹣2,b=1.
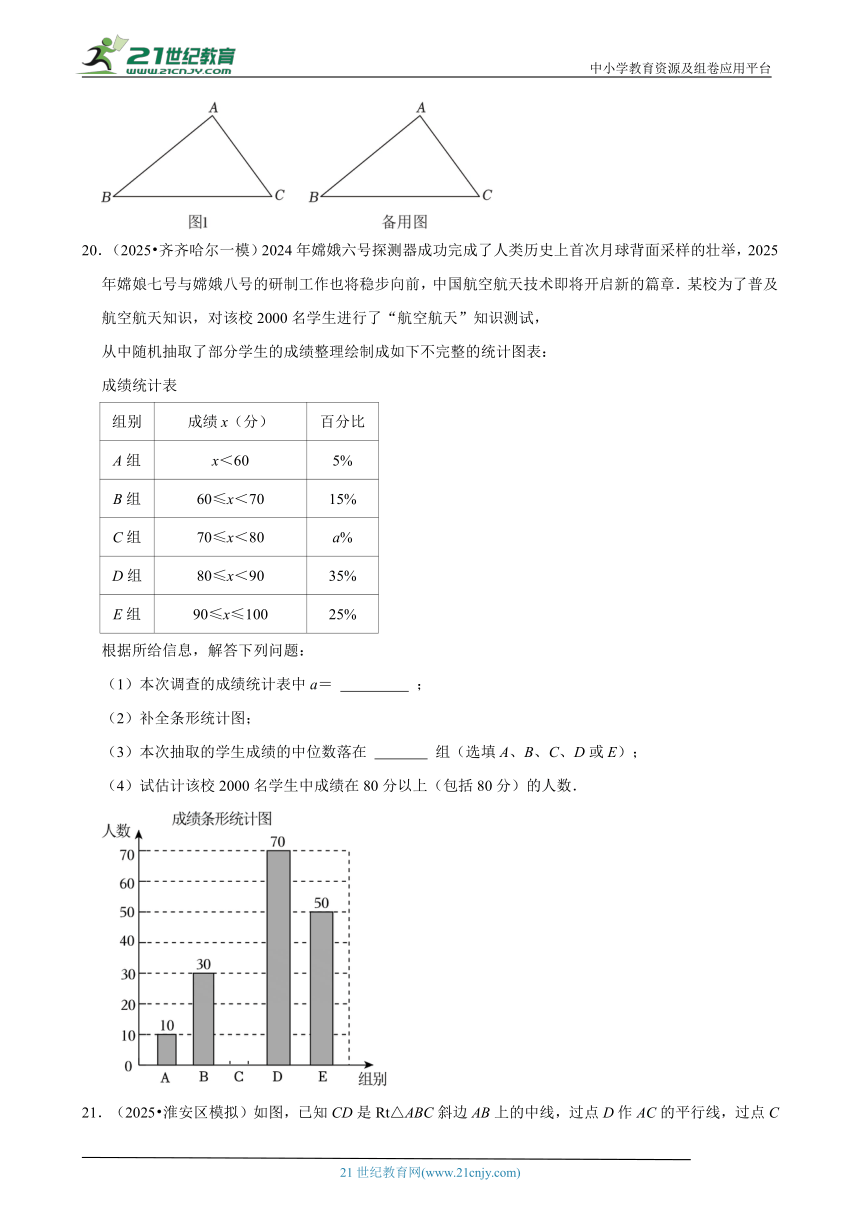
19.(2025 泰州二模)如图,△ABC中,∠ABC为锐角,AB<BC.点E为边BC上一点,点F为平面内一点,且四边形AECF为菱形.
(1)在图1中,请利用无刻度的直尺和圆规,作出菱形AECF.(不写作法,保留作图痕迹)
(2)若AC=5,BC=8,且△ABC的面积为16,则菱形AECF的边长为 .
20.(2025 齐齐哈尔一模)2024年嫦娥六号探测器成功完成了人类历史上首次月球背面采样的壮举,2025年嫦娘七号与嫦娥八号的研制工作也将稳步向前,中国航空航天技术即将开启新的篇章.某校为了普及航空航天知识,对该校2000名学生进行了“航空航天”知识测试,
从中随机抽取了部分学生的成绩整理绘制成如下不完整的统计图表:
成绩统计表
组别 成绩x(分) 百分比
A组 x<60 5%
B组 60≤x<70 15%
C组 70≤x<80 a%
D组 80≤x<90 35%
E组 90≤x≤100 25%
根据所给信息,解答下列问题:
(1)本次调查的成绩统计表中a= ;
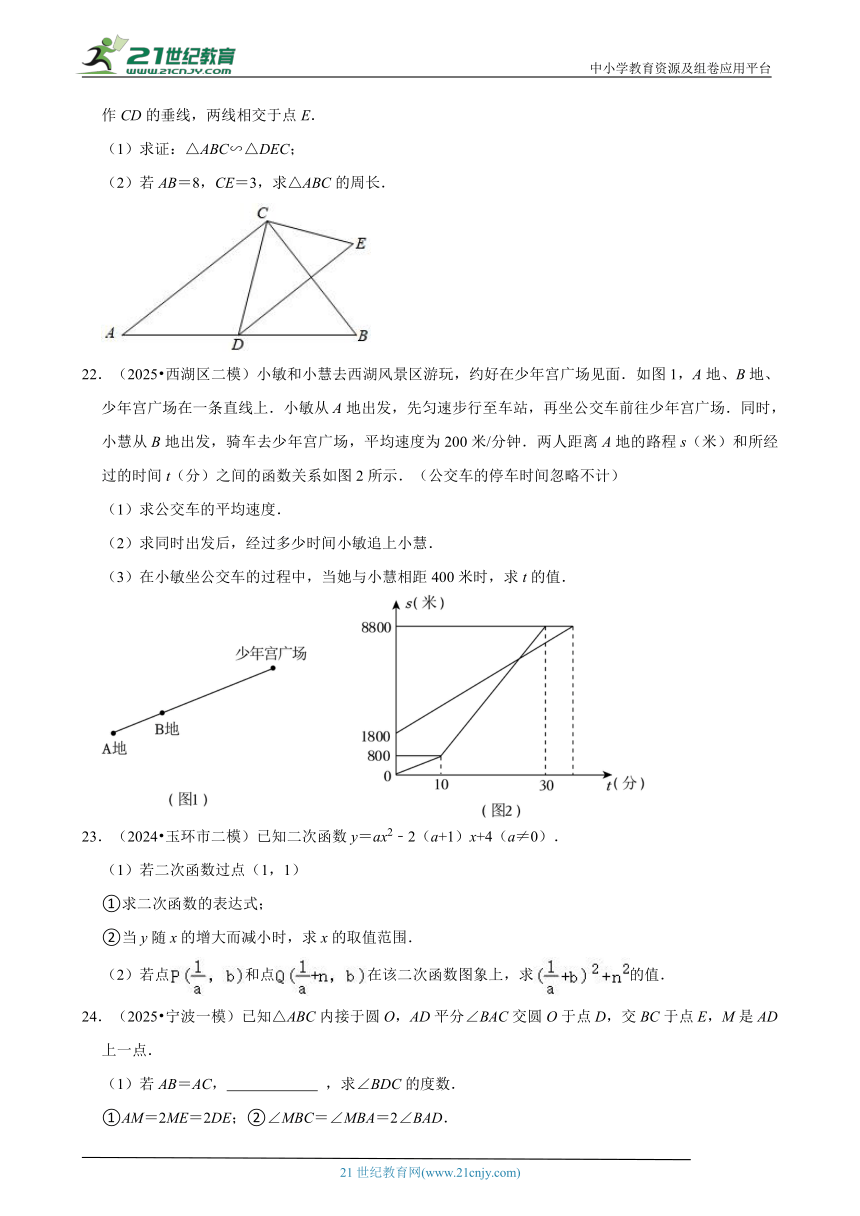
(2)补全条形统计图;
(3)本次抽取的学生成绩的中位数落在 组(选填A、B、C、D或E);
(4)试估计该校2000名学生中成绩在80分以上(包括80分)的人数.
21.(2025 淮安区模拟)如图,已知CD是Rt△ABC斜边AB上的中线,过点D作AC的平行线,过点C作CD的垂线,两线相交于点E.
(1)求证:△ABC∽△DEC;
(2)若AB=8,CE=3,求△ABC的周长.
22.(2025 西湖区二模)小敏和小慧去西湖风景区游玩,约好在少年宫广场见面.如图1,A地、B地、少年宫广场在一条直线上.小敏从A地出发,先匀速步行至车站,再坐公交车前往少年宫广场.同时,小慧从B地出发,骑车去少年宫广场,平均速度为200米/分钟.两人距离A地的路程s(米)和所经过的时间t(分)之间的函数关系如图2所示.(公交车的停车时间忽略不计)
(1)求公交车的平均速度.
(2)求同时出发后,经过多少时间小敏追上小慧.
(3)在小敏坐公交车的过程中,当她与小慧相距400米时,求t的值.
23.(2024 玉环市二模)已知二次函数y=ax2﹣2(a+1)x+4(a≠0).
(1)若二次函数过点(1,1)
①求二次函数的表达式;
②当y随x的增大而减小时,求x的取值范围.
(2)若点和点在该二次函数图象上,求的值.
24.(2025 宁波一模)已知△ABC内接于圆O,AD平分∠BAC交圆O于点D,交BC于点E,M是AD上一点.
(1)若AB=AC, ,求∠BDC的度数.
①AM=2ME=2DE;②∠MBC=∠MBA=2∠BAD.
(作答第(1)题时,先选择①或②填写在横线处,使题目完整,然后求解∠BDC的度数.)
(2)若AB=c,AE=m,AC=b,求DE的长.
(3)若∠MBC=∠MCA=∠MAB,求证:BC2=AB AC.
答案与解析
一、选择题:本题共10小题,每小题3分,共30分。在每小题给出的四个选项中,只有一项是符合题目要求的。
1.(2025 渝北区一模)的相反数是( )
A. B. C.﹣ D.﹣
【点拨】根据只有符号不同的两个数互为相反数,可得答案.
【解析】解:的相反数是﹣,
故选:C.
【点睛】本题考查了相反数,在一个数的前面加上负号就是这个数的相反数.
2.(2025 鹤山市一模)垃圾分类功在当代利在千秋,下列垃圾分类指引标志图形中,是轴对称图形又是中心对称图形的是( )
A.厨余垃圾Food Waste B.可回收物Recyclable
C.其他垃圾Residual Waste D.有害垃圾Hazardous Waste
【点拨】根据轴对称图形与中心对称图形的概念求解.
【解析】解:A、是轴对称图形,不是中心对称图形,故此选项不符合题意;
B、不是轴对称图形,不是中心对称图形,故此选项不符合题意;
C、不是轴对称图形,不是中心对称图形,故此选项不符合题意;
D、是轴对称图形,也是中心对称图形,故此选项符合题意.
故选:D.
【点睛】此题主要考查了中心对称图形与轴对称图形,轴对称图形的关键是寻找对称轴,图形两部分折叠后可重合,中心对称图形是要寻找对称中心,旋转180度后两部分重合.
3.(2024秋 娄底校级期末)电影《志愿军:存亡之战》以7.61亿元票房领跑2024年国庆档电影票房.其中数据7.61亿用科学记数法表示为( )
A.0.761×109 B.7.61×108 C.7.61×106 D.761×108
【点拨】科学记数法的表示形式为a×10n的形式,其中1≤|a|<10,n为整数.确定n的值时,要看把原数变成a时,小数点移动了多少位,n的绝对值与小数点移动的位数相同.当原数绝对值≥10时,n是正数;当原数的绝对值<1时,n是负数.
【解析】解:7.61亿=761000000=7.61×108.
故选:B.
【点睛】此题考查科学记数法的表示方法.科学记数法的表示形式为a×10n的形式,其中1≤|a|<10,n为整数,表示时关键要正确确定a的值以及n的值.
4.(2025 华蓥市模拟)下列计算正确的是( )
A.(m3)5=m15 B.m4+m4=m8 C.m6÷m2=m3 D.(m+1)2=m2+1
【点拨】根据幂的乘方,合并同类项,同底数幂的除法,完全平方和公式的运算法则,对各选项分析判断求解即可.
【解析】解:根据整式的相关运算法则逐项分析判断如下:
A.(m3)5=m15,正确,符合题意;
B.m4+m4=2m4,原式计算错误,不符合题意;
C.m6÷m2=m4,原式计算错误,不符合题意;
D.(m+1)2=m2+2m+1,原式计算错误,不符合题意.
故选:A.
【点睛】本题考查了幂的乘方,合并同类项,同底数幂的除法,完全平方和公式,掌握以上运算法则是解题的关键.
5.(2025 盐城一模)若点A(﹣3,y1),B(﹣1,y2),C(2,y3)在反比例函数的图象上,则y1,y2,y3的大小关系是( )
A.y1<y2<y3 B.y2<y1<y3 C.y3<y2<y1 D.y2<y3<y1
【点拨】根据k=7>0,可得反比例函数图象和增减性,即可进行比较.
【解析】解∵k=7>0,
∴反比例函数经过第一、三象限,且在每一象限内,y随着x增大而减小,
根据A,B,C点横坐标,可知点A,B在第三象限,C在第一象限,
﹣3<﹣1,2>0,
∴y2<y1<y3;
故选:B.
【点睛】本题考查了反比例函数的图象和性质,熟练掌握反比例函数的增减性是解题的关键.
6.(2025 吉林二模)关于x的不等式2x﹣a≤﹣1的解集如图所示,那么a的值是( )
A.﹣2 B.2 C.﹣3 D.3
【点拨】先求出不等式的解集,然后根据数轴写出不等式的解集,从而可以得到关于a的方程,再求解即可.
【解析】解:由不等式2x﹣a≤﹣1可得x≤,
由数轴可得,该不等式的解集为x≤1,
∴=1,
解得a=3,
故选:D.
【点睛】本题考查解一元一次不等式、在数轴上表示不等式的解集,解答本题的关键是明确解一元一次不等式的方法.
7.(2025 崂山区一模)某中学足球队16名队员的年龄情况如下表,则这些队员年龄的众数和中位数分别为( )
年龄(单位岁) 14 15 16 17 18
人数 2 4 5 3 2
A.15,16 B.16,16.5 C.16,16 D.17,16.5
【点拨】根据中位数、众数的意义进行计算即可.
【解析】解:足球队16名队员的年龄出现次数最多的是16岁,共出现5次,
因此众数是16岁;
将这16名队员的年龄从小到大排列,处在中间位置的两个数都是16岁,
因此中位数是16岁,
故选:C.
【点睛】本题考查中位数、众数,理解中位数、众数的意义,掌握中位数、众数的计算方法是正确解题的关键.
8.(2025 西宁一模)某环卫公司为清理卫生死角内的垃圾,调用甲车3h,只清理了一半垃圾,为了加快进步,再调用乙车,两车合作1.2h清理完另一半垃圾,设乙车单独清理全部垃圾的时间为xh,根据题意可列出方程为( )
A.+=1 B.+= C.+=1 D.+=
【点拨】首先明确将总工作量看作单位1,则甲乙合作完成的工作量=;根据甲的工作量为,乙的工作量为:,可得方程.
【解析】解:甲的工作效率为,乙的工作效率为,所以方程为:+=.
故选:B.
【点睛】本题考查分式方程的应用,找到等量关系列出方程是解题关键.
9.(2025 义乌市二模)如图,在四边形ABCD中,已知AD∥BC,∠B=90°,,对角线AC平分∠BAD,∠DCA:∠BCA=2:3,则CD的值为( )
A. B. C. D.
【点拨】根据角平分线的意义和平行线的性质可证明△ABC是等腰直角三角形,由勾股定理得AC=2,由∠DCA:∠BCA=2:3得∠ACD=30°,过点D作DE⊥AC,可证明△ADE是等腰直角三角形,设DE=AE=x,则CE=2﹣x,由可求出x的值,再根据可求出CD的长.
【解析】解:∵AD∥BC,∠B=90°,AB=,
∴∠B+∠BAD=180°,
∴∠BAD=90°,
∵AC平分∠BAD,
∴,
∵AD∥BC,
∴∠DAC=∠ACB,
∴∠BAC=∠ACB=45°,
∴,
∴,
∵∠DCA:∠BCA=2:3,
∴;
如图,过点D作DE⊥AC,
∴∠AED=90°,
∵∠DAE=45°,
∴∠ADE=∠DAE=45°,
∴AE=DE,
设DE=AE=x,则CE=2﹣x,
∵,
∴
∴,即,
∵,
∴,
故选:D.
【点睛】本题主要考查等腰直角三角形的判定与性质,平行线的性质,角平分线的性质,熟知以上知识是解题的关键.
10.(2025 滨江区一模)如图,AB,CD是⊙O的直径,AB⊥CD,点E为劣弧(不含端点)上一点,连接AE,CE,分别交OD,OB于点F,G.若⊙O的半径为1,记OF=x,BG=y,则下列代数式的值不变的是( )
A.2x﹣y B. C.2y﹣x D.
【点拨】如图,由题可得∠1=∠2=45°,,导角证明△ACF∽△GAC,则,化简即可得到,即可判断.
【解析】解:如图,连接AC
∵AB,CD是⊙O的直径,AB⊥CD,OA=OC=1,
∴∠1=∠2=45°,,
设∠OAF=α,
则∠CAF=∠1+∠OAF=45°+α,,
∴∠CAF=∠AGC,
∴△ACF∽△GAC,
∴,即,
∴(1+x)(2﹣y)=2,
∴2﹣y+2x﹣xy=2,
∴2x﹣y=xy,
两边同时除以xy得:,
故D符合题意,而A、B、C代数式的值均不能证明不变,故不符合题意,
故选:D.
【点睛】本题考查了圆周角定理,相似三角形的判定与性质,勾股定理等知识点,正确添加辅助线,熟练掌握各知识点并灵活运用是解题的关键.
二、填空题:本题共6小题,每小题3分,共18分。
11.(2024 新丰县一模)因式分解:m2﹣25= (m+5)(m﹣5) .
【点拨】原式利用平方差公式分解即可.
【解析】解:原式=(m+5)(m﹣5),
故答案为:(m+5)(m﹣5)
【点睛】此题考查了因式分解﹣运用公式法,熟练掌握平方差公式是解本题的关键.
12.(2025 上虞区二模)若分式的值为1,则字母x的取值为 2 .
【点拨】由题意易得=1,解方程后并检验即可.
【解析】解:由题意得=1,
去分母得:x+2=4,
解得:x=2,
经检验,x=2是分式方程的解,
故答案为:2.
【点睛】本题考查解分式方程,熟练掌握解方程的方法是解题的关键.
13.(2025 濠江区一模)一个袋子中有2个白球和若干个黑球,它们除了颜色外都相同,随机从中摸一个球,恰好摸到黑球的概率是,则袋子中有 3 个黑球.
【点拨】设袋子中有x个黑球,由此列式求解即可.
【解析】解:设袋子中有x个黑球,
∵随机从中摸一个球,恰好摸到黑球的概率是,
∴,
解得,x=3,
检验,当x=3时,原分式方程有意义,
∴袋子中有3个黑球,
故答案为:3.
【点睛】本题考查了概率公式,熟记概率公式熟解题的关键.
14.(2025 建邺区一模)如图,在矩形ABCD中,点A的坐标是(0,﹣1),点B的坐标是(2,0),点C在y轴上.若反比例函数的图象经过点D,则k= ﹣6 .
【点拨】根据三角形相似,可求出D点坐标,把D点坐标代入反比例函数解析式中,即可求出k的值.
【解析】
解:过点D作DE垂直于y轴,并交y轴于点E,
∠CAB+∠ABO=90°,
∠CAB+∠ACB=90°
∴∠ABO=∠ACB,
在Rt△OAB和Rt△OCB中,
∠AOB=∠COB,
∠ABO=∠ACB,
∴Rt△OAB和∽Rt△OCB,
∴=,
∵OA=1,OB=2,
∴OC=4,
∵DC∥AB,
∴∠DCA=∠CAB,
∵DC=AB,∠DCA=∠CAB,∠DEC=∠BOA,
∴△DEC=△BOA,
∴DE=OB,CE=AO,
∴D点坐标为(﹣2,3),
∴点D在反比例函数上,
∴y=,即3=,
∴k=﹣6.
故答案为:﹣6.
【点睛】本题主要考查了反比例函数的性质,熟练掌握反比例函数的性质是解题的关键.
15.(2025 济宁二模)如图,⊙O半径为,正方形ABCD内接于⊙O,点E在上运动,连接BE,作AF⊥BE,垂足为F,连接CF.则CF长的最小值为 .
【点拨】如图,取AB的中点K,以AB为直径作⊙K,想办法求出FK,CK,根据CF≥CK﹣FK即可解决问题.
【解析】解:如图,取AB的中点K,以AB为直径作⊙K,
∵AF⊥BE,
∴∠AFB=90°,
∵AK=BK,
∴KF=AK=BK,
∵正方形ABCD的外接圆的半径为,
∴AB=BC==2,
∴KF=AK=KB=1,
∵∠CBK=90°,
∴CK===,
∵CF≥CK﹣KF,
∴CF≥﹣1,
∴CF的最小值为﹣1.
故答案为﹣1.
【点睛】本题考查正多边形与圆,圆周角定理,解直角三角形等知识,解题的关键是学会用转化的思想思考问题,属于中考常考题型.
16.(2025 宣城二模)如图,正方形ABCD的边长为6,点E,F分别在BC,AD上.将该正方形沿EF折叠,使点A落在CD边上的点M处,连接AM,与折痕EF交于点P.
(1)若M是CD的中点,则AF的长为 ;
(2)若G为MN的中点,随着折痕EF位置的变化,PG+PM的最小值为 3 .
【点拨】(1)由折叠得EF是AM的中垂线,根据线段垂直平分线的性质求出AF=MF,再根据勾股定理求出AF的长.
(2)取AB的中点Q,根据两点之间线段最短得出PG+PM的最小值.
【解析】解:(1)根据折叠的性质可得EF是AM的垂直平分线,
∴AF=MF,
设AF=MF=x,则DF=6﹣x.
∵M是CD的中点,
∴DM=CD=3,
在Rt△DFM中,DF2+DM2=FM2,
即(6﹣x)2+32=x2,
解得x=,
即AF的长为,
故答案为:;
(2)如图,取AB的中点Q,连接QP,PG,PD,由折叠的对称性可知PQ=PG.
∵G为MN的中点,△ADM为直角三角形,
∴PD=AM=PM,
∴PG+PM=PQ+DP≥DQ,
当且仅当D,P,Q三点共线时PG+PM最小,最小值===3,
故答案为:
【点睛】本题考查了折叠的性质、正方形的性质、勾股定理、最值问题,第二问有难度,解题的关键是取AB的中点Q,确定PG+PM=PQ+DP,属于中考常考题型.
三.解答题(共8小题,其中第17-22题每题8分,第23题10分,第24题每题12分,共72分)
17.(2025 西宁一模)计算:.
【点拨】先计算乘方、零指数幂、特殊角的三角函数值、二次根式,再计算乘法,最后计算加减即可得出答案.
【解析】解:
=
=
=0.
【点睛】此题主要考查了实数的混合运算,熟练掌握乘方运算的法则,零指数幂的运算法则,二次根式的化简,熟记特殊角的三角函数值是解决问题的关键.
18.(2025 乾安县模拟)先化简,再求值:(2a+b)2﹣(b﹣2a)(2a+b),其中a=﹣2,b=1.
【点拨】先根据完全平方公式和平方差公式进行计算再合并同类项,最后代入求出答案即可.
【解析】解:(2a+b)2﹣(b﹣2a)(2a+b)
=(4a2+4ab+b2)﹣(b2﹣4a2)
=4a2+4ab+b2﹣b2+4a2
=8a2+4ab,
当a=﹣2,b=1时,
原式=8×(﹣2)2+4×(﹣2)×1
=8×4﹣8
=32﹣8
=24.
【点睛】本题考查了整式的化简求值,能正确根据整式的运算法则进行计算是解此题的关键,注意运算顺序.
19.(2025 泰州二模)如图,△ABC中,∠ABC为锐角,AB<BC.点E为边BC上一点,点F为平面内一点,且四边形AECF为菱形.
(1)在图1中,请利用无刻度的直尺和圆规,作出菱形AECF.(不写作法,保留作图痕迹)
(2)若AC=5,BC=8,且△ABC的面积为16,则菱形AECF的边长为 .
【点拨】(1)作线段AC的垂直平分线MN,MN交BC于点E,以C为圆心,CE为半径作弧交MN于点F,连接AF,CF,四边形AECF即为所求.
(2)过点A作AH⊥BC于点H.利用面积法求出AH,设AE=EC=x,利用勾股定理构建方程求出x即可.
【解析】解:(1)如图1中,四边形AECF即为所求;
(2)过点A作AH⊥BC于点H.
∵△ABC的面积= BC AH,
∴AH==4,
∴CH===3,
设AE=EC=x,则有x2=42+(x﹣3)2,
解得x=.
∴AE=EC=,
故答案为:.
【点睛】本题考查作图﹣复杂作图,菱形的判定和性质,勾股定理,解题的关键是理解题意,灵活运用所学知识解决问题
20.(2025 齐齐哈尔一模)2024年嫦娥六号探测器成功完成了人类历史上首次月球背面采样的壮举,2025年嫦娘七号与嫦娥八号的研制工作也将稳步向前,中国航空航天技术即将开启新的篇章.某校为了普及航空航天知识,对该校2000名学生进行了“航空航天”知识测试,
从中随机抽取了部分学生的成绩整理绘制成如下不完整的统计图表:
成绩统计表
组别 成绩x(分) 百分比
A组 x<60 5%
B组 60≤x<70 15%
C组 70≤x<80 a%
D组 80≤x<90 35%
E组 90≤x≤100 25%
根据所给信息,解答下列问题:
(1)本次调查的成绩统计表中a= 20 ;
(2)补全条形统计图;
(3)本次抽取的学生成绩的中位数落在 D 组(选填A、B、C、D或E);
(4)试估计该校2000名学生中成绩在80分以上(包括80分)的人数.
【点拨】(1)利用1减去其他四组所占的百分比即可得a的值;
(2)先根据A的条形统计图和统计表信息求出此次调查抽取的总人数,再乘以C组所占百分比可得C组的人数,据此补全条形统计图即可得;
(3)根据中位数的定义求解即可得;
(4)利用该校学生总人数乘以成绩在80分以上(包括80分)的人数所占的百分比即可得.
【解析】解:(1)利用1减去其他四组所占的百分比可得:
a%=1﹣5%﹣15%﹣35%﹣25%=20%,
∴a=20,
故答案为:20.
(2)此次调查抽取的总人数为10÷5%=200(名),
则C组的人数为200×20%=40(名),
补全条形统计图如下:
(3)∵10+30+40=80,10+30+40+70=150,
∴排在第100个数和第101个数均在D组,
∴被抽取的学生成绩的中位数落在D组,
故答案为:D.
(4)2000×(35%+25%)=1200(名),
答:估计该校1200名学生中成绩在80分以上(包括80分)的人数为1200名.
【点睛】本题考查了统计表、条形统计图、中位数、利用样本估计总体,熟练掌握统计调查的相关知识是解题关键.
21.(2025 淮安区模拟)如图,已知CD是Rt△ABC斜边AB上的中线,过点D作AC的平行线,过点C作CD的垂线,两线相交于点E.
(1)求证:△ABC∽△DEC;
(2)若AB=8,CE=3,求△ABC的周长.
【点拨】(1)先根据斜边上的中线性质得到DA=DC,则∠A=∠ACD,再根据平行线的性质得到∠ACD=∠CDE,所以∠A=∠CDE,加上∠ACB=∠DCE=90°,则根据相似三角形的判定方法可判断△ABC∽△DEC;
(2)先利用斜边上的中线性质得到CD=AB=4,再利用勾股定理计算出DE=5,接着根据相似三角形的性质得到==,然后求出AC、BC,从而得到△ABC的周长.
【解析】(1)证明:∵DC⊥CE,
∴∠DCE=90°,
∵CD是Rt△ABC斜边AB上的中线,
∴DA=DC,
∴∠A=∠ACD,
∵AC∥DE,
∴∠ACD=∠CDE,
∴∠A=∠CDE,
∵∠ACB=∠DCE,
∴△ABC∽△DEC;
(2)解:∵CD是Rt△ABC斜边AB上的中线,
∴CD=AB=4,
在Rt△DCE中,DE===5,
∵△ABC∽△DEC,
∴==,即==,
∴AC=,BC=,
∴△ABC的周长=++8=.
【点睛】本题考查了相似三角形的判定与性质:在判定两个三角形相似时,应注意利用图形中已有的公共角、公共边等隐含条件;灵活运用相似三角形的性质进行几何计算是解决问题的关键.也考查了直角三角形斜边上的中线性质.
22.(2025 西湖区二模)小敏和小慧去西湖风景区游玩,约好在少年宫广场见面.如图1,A地、B地、少年宫广场在一条直线上.小敏从A地出发,先匀速步行至车站,再坐公交车前往少年宫广场.同时,小慧从B地出发,骑车去少年宫广场,平均速度为200米/分钟.两人距离A地的路程s(米)和所经过的时间t(分)之间的函数关系如图2所示.(公交车的停车时间忽略不计)
(1)求公交车的平均速度.
(2)求同时出发后,经过多少时间小敏追上小慧.
(3)在小敏坐公交车的过程中,当她与小慧相距400米时,求t的值.
【点拨】(1)根据速度=路程÷时间计算即可;
(2)分别写出当10≤t≤30时小敏距离A地的路程s和所经过的时间t之间的函数关系式、小慧距离A地的路程s和所经过的时间t之间的函数关系式,令两函数值相等列关于t的一元一次方程并求解即可;
(3)当10≤t≤30时,令两函数值差的绝对值为400,列关于t的方程并求解即可.
【解析】解:(1)(8800﹣800)÷(30﹣10)=400(米/分).
答:公交车的平均速度是400米/分.
(2)当10≤t≤30时,小敏距离A地的路程s和所经过的时间t之间的函数关系式为s=800+400(t﹣10)=400t﹣3200,
小慧距离A地的路程s和所经过的时间t之间的函数关系式为s=200t+1800,
当小敏追上小慧时,得400t﹣3200=200t+1800,
解得t=25.
答:同时出发后,经过25分小敏追上小慧.
(3)当10≤t≤30时,得|400t﹣3200﹣(200t+1800)|=400,
解得t=23或27.
答:小敏坐公交车的过程中,当她与小慧相距400米时,求t的值为23或27.
【点睛】本题考查一次函数的应用,掌握时间、速度和路程之间的关系是解题的关键.
23.(2024 玉环市二模)已知二次函数y=ax2﹣2(a+1)x+4(a≠0).
(1)若二次函数过点(1,1)
①求二次函数的表达式;
②当y随x的增大而减小时,求x的取值范围.
(2)若点和点在该二次函数图象上,求的值.
【点拨】(1)①依据题意,由二次函数过点(1,1),从而可得1=a﹣2(a+1)+4,求出a后即可得解;
②依据题意,由①y=x2﹣4x+4=(x﹣2)2,结合二次函数的性质可以判断得解;
(2)依据题意,先求出抛物线对称轴,在根据P,Q关于对称轴对称求出n=2,再把点P坐标代入抛物线求出b=2﹣,再求出(+b)2+n2的值;
【解析】解:(1)①∵二次函数过点(1,1),
∴1=a﹣2(a+1)+4.
∴a=1.
∴二次函数的表达式为y=x2﹣4x+4.
②由①y=x2﹣4x+4=(x﹣2)2,
∴当x<2时,y随x的增大而减小.
∴当y随x的增大而减小时,x<2.
(2)∵y=ax2﹣2(a+1)x+4(a≠0),
∴抛物线对称轴为直线x=﹣=1+.
∵点P(,b)和点Q(+n,b)关于对称轴对称,
∴=1+.
∴n=2.
把P(,b)代入函数解析式得:a×﹣2(a+1)×+4=b,
解得b=2﹣.
∴(+b)2+n2=(+2﹣)2+22=8.
【点睛】本题主要考查二次函数图象与系数的关系,解题关键是掌握二次函数的性质.
24.(2025 宁波一模)已知△ABC内接于圆O,AD平分∠BAC交圆O于点D,交BC于点E,M是AD上一点.
(1)若AB=AC, ①(或②) ,求∠BDC的度数.
①AM=2ME=2DE;②∠MBC=∠MBA=2∠BAD.
(作答第(1)题时,先选择①或②填写在横线处,使题目完整,然后求解∠BDC的度数.)
(2)若AB=c,AE=m,AC=b,求DE的长.
(3)若∠MBC=∠MCA=∠MAB,求证:BC2=AB AC.
【点拨】(1)当选择①时,由题意易得AE⊥BC,BE=EC,∠BAD=∠CAD,然后可得AD是直径,则有点M是圆心,且四边形BDCM是平行四边形,进而问题可求解;若选择②,由题意易得AE⊥BC,∠BAD=∠CAD,设∠BAD=α,则有∠MBC=∠MBA=2α=∠BAC,然后可得方程2α+3α=90°,进而问题可求解;
(2)由题意易得∠BAD=∠CAD,则可证△ABD∽△AEC,则有,进而问题可求解;
(3)先证明△ABC∽△BMD,△ABC∽△MDC,则有,,然后根据BD=CD可得,进而问题可求证.
【解析】(1)解:当选择①时;
∵已知△ABC内接于圆O,AD平分∠BAC交圆O于点D,AB=AC,
∴AE⊥BC,BE=EC,∠BAD=∠CAD,
∴,
∴AD是直径,
∵AM=2ME=2DE,
∴ME=DE,AM=DM,
∴点M是圆心,且四边形BDCM是平行四边形,
∵BM=CM,
∴四边形BDCM是菱形,
∴BM=BD=DM=CD=MC,
∴△BDM,△CDM都为等边三角形,
∴∠BDM=∠CDM=60°,
∴∠BDC=120°;
若选择②;
∵已知△ABC内接于圆O,AD平分∠BAC交圆O于点D,AB=AC,
∴AE⊥BC,∠BAD=∠CAD,
由∠MBC=∠MBA=2∠BAD可设∠BAD=α,则有∠MBC=∠MBA=2α=∠BAC,
∴∠BMD=∠MBA+∠BAD=3α,
∵∠MEB=90°,
∴∠MBC+∠BME=90°,即2α+3α=90°,
∴α=18°,
∴∠BAC=2α=36°,
∵四边形ABDC内接于圆O,
∴∠BDC=180°﹣∠BAC=144°,
故答案为:①(或②);
(2)解:已知△ABC内接于圆O,AD平分∠BAC交圆O于点D,
∴∠BAD=∠CAD,
∵∠ADB=∠ACE,
∴△ABD∽△AEC,
∴,
∵AB=c,AE=m,AC=b,
∴,
∴,
∴;
(3)证明:已知△ABC内接于圆O,AD平分∠BAC交圆O于点D,
∴∠BAD=∠CAD,
∵∠MBC=∠MCA=∠MAB,
∴∠MBC=∠MCA=∠MAB=∠CAD,
∴∠BMD=∠BAM+∠ABM=∠ABM+∠MBC=∠ABC,
∵∠BDM=∠ACB,
∴△ABC∽△BMD,
∴,即,
∵∠DMC=∠CAD+∠ACM=2∠CAD,
∴∠BAC=∠DMC,
∵∠ABC=∠MDC,
∴△ABC∽△MDC,
∴,
∴,
∵∠BAD=∠CAD,
∴,
∴BD=CD,
∴,
∴,
∴BC2=AB AC.
【点睛】本题属于圆的综合题,主要考查垂径定理、菱形的性质与判定、圆周角的性质、圆内接四边形的性质及相似三角形的性质与判定,熟练掌握垂径定理、菱形的性质与判定、圆周角的性质、圆内接四边形的性质及相似三角形的性质与判定是解题的关键.
21世纪教育网 www.21cnjy.com 精品试卷·第 2 页 (共 2 页)
HYPERLINK "http://21世纪教育网(www.21cnjy.com)
" 21世纪教育网(www.21cnjy.com)
2025年浙江省中考数学模拟试卷(9)
一、选择题:本题共10小题,每小题3分,共30分。在每小题给出的四个选项中,只有一项是符合题目要求的。
1.(2025 渝北区一模)的相反数是( )
A. B. C.﹣ D.﹣
2.(2025 鹤山市一模)垃圾分类功在当代利在千秋,下列垃圾分类指引标志图形中,是轴对称图形又是中心对称图形的是( )
A.厨余垃圾Food Waste B.可回收物Recyclable
C.其他垃圾Residual Waste D.有害垃圾Hazardous Waste
3.(2024秋 娄底校级期末)电影《志愿军:存亡之战》以7.61亿元票房领跑2024年国庆档电影票房.其中数据7.61亿用科学记数法表示为( )
A.0.761×109 B.7.61×108 C.7.61×106 D.761×108
4.(2025 华蓥市模拟)下列计算正确的是( )
A.(m3)5=m15 B.m4+m4=m8 C.m6÷m2=m3 D.(m+1)2=m2+1
5.(2025 盐城一模)若点A(﹣3,y1),B(﹣1,y2),C(2,y3)在反比例函数的图象上,则y1,y2,y3的大小关系是( )
A.y1<y2<y3 B.y2<y1<y3 C.y3<y2<y1 D.y2<y3<y1
6.(2025 吉林二模)关于x的不等式2x﹣a≤﹣1的解集如图所示,那么a的值是( )
A.﹣2 B.2 C.﹣3 D.3
7.(2025 崂山区一模)某中学足球队16名队员的年龄情况如下表,则这些队员年龄的众数和中位数分别为( )
年龄(单位岁) 14 15 16 17 18
人数 2 4 5 3 2
A.15,16 B.16,16.5 C.16,16 D.17,16.5
8.(2025 西宁一模)某环卫公司为清理卫生死角内的垃圾,调用甲车3h,只清理了一半垃圾,为了加快进步,再调用乙车,两车合作1.2h清理完另一半垃圾,设乙车单独清理全部垃圾的时间为xh,根据题意可列出方程为( )
A.+=1 B.+= C.+=1 D.+=
9.(2025 义乌市二模)如图,在四边形ABCD中,已知AD∥BC,∠B=90°,,对角线AC平分∠BAD,∠DCA:∠BCA=2:3,则CD的值为( )
A. B. C. D.
10.(2025 滨江区一模)如图,AB,CD是⊙O的直径,AB⊥CD,点E为劣弧(不含端点)上一点,连接AE,CE,分别交OD,OB于点F,G.若⊙O的半径为1,记OF=x,BG=y,则下列代数式的值不变的是( )
A.2x﹣y B. C.2y﹣x D.
二、填空题:本题共6小题,每小题3分,共18分。
11.(2024 新丰县一模)因式分解:m2﹣25= .
12.(2025 上虞区二模)若分式的值为1,则字母x的取值为 .
13.(2025 濠江区一模)一个袋子中有2个白球和若干个黑球,它们除了颜色外都相同,随机从中摸一个球,恰好摸到黑球的概率是,则袋子中有 个黑球.
14.(2025 建邺区一模)如图,在矩形ABCD中,点A的坐标是(0,﹣1),点B的坐标是(2,0),点C在y轴上.若反比例函数的图象经过点D,则k= .
15.(2025 济宁二模)如图,⊙O半径为,正方形ABCD内接于⊙O,点E在上运动,连接BE,作AF⊥BE,垂足为F,连接CF.则CF长的最小值为 .
16.(2025 宣城二模)如图,正方形ABCD的边长为6,点E,F分别在BC,AD上.将该正方形沿EF折叠,使点A落在CD边上的点M处,连接AM,与折痕EF交于点P.
(1)若M是CD的中点,则AF的长为 ;
(2)若G为MN的中点,随着折痕EF位置的变化,PG+PM的最小值为 .
三.解答题(共8小题,其中第17-22题每题8分,第23题10分,第24题每题12分,共72分)
17.(2025 西宁一模)计算:.
18.(2025 乾安县模拟)先化简,再求值:(2a+b)2﹣(b﹣2a)(2a+b),其中a=﹣2,b=1.
19.(2025 泰州二模)如图,△ABC中,∠ABC为锐角,AB<BC.点E为边BC上一点,点F为平面内一点,且四边形AECF为菱形.
(1)在图1中,请利用无刻度的直尺和圆规,作出菱形AECF.(不写作法,保留作图痕迹)
(2)若AC=5,BC=8,且△ABC的面积为16,则菱形AECF的边长为 .
20.(2025 齐齐哈尔一模)2024年嫦娥六号探测器成功完成了人类历史上首次月球背面采样的壮举,2025年嫦娘七号与嫦娥八号的研制工作也将稳步向前,中国航空航天技术即将开启新的篇章.某校为了普及航空航天知识,对该校2000名学生进行了“航空航天”知识测试,
从中随机抽取了部分学生的成绩整理绘制成如下不完整的统计图表:
成绩统计表
组别 成绩x(分) 百分比
A组 x<60 5%
B组 60≤x<70 15%
C组 70≤x<80 a%
D组 80≤x<90 35%
E组 90≤x≤100 25%
根据所给信息,解答下列问题:
(1)本次调查的成绩统计表中a= ;
(2)补全条形统计图;
(3)本次抽取的学生成绩的中位数落在 组(选填A、B、C、D或E);
(4)试估计该校2000名学生中成绩在80分以上(包括80分)的人数.
21.(2025 淮安区模拟)如图,已知CD是Rt△ABC斜边AB上的中线,过点D作AC的平行线,过点C作CD的垂线,两线相交于点E.
(1)求证:△ABC∽△DEC;
(2)若AB=8,CE=3,求△ABC的周长.
22.(2025 西湖区二模)小敏和小慧去西湖风景区游玩,约好在少年宫广场见面.如图1,A地、B地、少年宫广场在一条直线上.小敏从A地出发,先匀速步行至车站,再坐公交车前往少年宫广场.同时,小慧从B地出发,骑车去少年宫广场,平均速度为200米/分钟.两人距离A地的路程s(米)和所经过的时间t(分)之间的函数关系如图2所示.(公交车的停车时间忽略不计)
(1)求公交车的平均速度.
(2)求同时出发后,经过多少时间小敏追上小慧.
(3)在小敏坐公交车的过程中,当她与小慧相距400米时,求t的值.
23.(2024 玉环市二模)已知二次函数y=ax2﹣2(a+1)x+4(a≠0).
(1)若二次函数过点(1,1)
①求二次函数的表达式;
②当y随x的增大而减小时,求x的取值范围.
(2)若点和点在该二次函数图象上,求的值.
24.(2025 宁波一模)已知△ABC内接于圆O,AD平分∠BAC交圆O于点D,交BC于点E,M是AD上一点.
(1)若AB=AC, ,求∠BDC的度数.
①AM=2ME=2DE;②∠MBC=∠MBA=2∠BAD.
(作答第(1)题时,先选择①或②填写在横线处,使题目完整,然后求解∠BDC的度数.)
(2)若AB=c,AE=m,AC=b,求DE的长.
(3)若∠MBC=∠MCA=∠MAB,求证:BC2=AB AC.
答案与解析
一、选择题:本题共10小题,每小题3分,共30分。在每小题给出的四个选项中,只有一项是符合题目要求的。
1.(2025 渝北区一模)的相反数是( )
A. B. C.﹣ D.﹣
【点拨】根据只有符号不同的两个数互为相反数,可得答案.
【解析】解:的相反数是﹣,
故选:C.
【点睛】本题考查了相反数,在一个数的前面加上负号就是这个数的相反数.
2.(2025 鹤山市一模)垃圾分类功在当代利在千秋,下列垃圾分类指引标志图形中,是轴对称图形又是中心对称图形的是( )
A.厨余垃圾Food Waste B.可回收物Recyclable
C.其他垃圾Residual Waste D.有害垃圾Hazardous Waste
【点拨】根据轴对称图形与中心对称图形的概念求解.
【解析】解:A、是轴对称图形,不是中心对称图形,故此选项不符合题意;
B、不是轴对称图形,不是中心对称图形,故此选项不符合题意;
C、不是轴对称图形,不是中心对称图形,故此选项不符合题意;
D、是轴对称图形,也是中心对称图形,故此选项符合题意.
故选:D.
【点睛】此题主要考查了中心对称图形与轴对称图形,轴对称图形的关键是寻找对称轴,图形两部分折叠后可重合,中心对称图形是要寻找对称中心,旋转180度后两部分重合.
3.(2024秋 娄底校级期末)电影《志愿军:存亡之战》以7.61亿元票房领跑2024年国庆档电影票房.其中数据7.61亿用科学记数法表示为( )
A.0.761×109 B.7.61×108 C.7.61×106 D.761×108
【点拨】科学记数法的表示形式为a×10n的形式,其中1≤|a|<10,n为整数.确定n的值时,要看把原数变成a时,小数点移动了多少位,n的绝对值与小数点移动的位数相同.当原数绝对值≥10时,n是正数;当原数的绝对值<1时,n是负数.
【解析】解:7.61亿=761000000=7.61×108.
故选:B.
【点睛】此题考查科学记数法的表示方法.科学记数法的表示形式为a×10n的形式,其中1≤|a|<10,n为整数,表示时关键要正确确定a的值以及n的值.
4.(2025 华蓥市模拟)下列计算正确的是( )
A.(m3)5=m15 B.m4+m4=m8 C.m6÷m2=m3 D.(m+1)2=m2+1
【点拨】根据幂的乘方,合并同类项,同底数幂的除法,完全平方和公式的运算法则,对各选项分析判断求解即可.
【解析】解:根据整式的相关运算法则逐项分析判断如下:
A.(m3)5=m15,正确,符合题意;
B.m4+m4=2m4,原式计算错误,不符合题意;
C.m6÷m2=m4,原式计算错误,不符合题意;
D.(m+1)2=m2+2m+1,原式计算错误,不符合题意.
故选:A.
【点睛】本题考查了幂的乘方,合并同类项,同底数幂的除法,完全平方和公式,掌握以上运算法则是解题的关键.
5.(2025 盐城一模)若点A(﹣3,y1),B(﹣1,y2),C(2,y3)在反比例函数的图象上,则y1,y2,y3的大小关系是( )
A.y1<y2<y3 B.y2<y1<y3 C.y3<y2<y1 D.y2<y3<y1
【点拨】根据k=7>0,可得反比例函数图象和增减性,即可进行比较.
【解析】解∵k=7>0,
∴反比例函数经过第一、三象限,且在每一象限内,y随着x增大而减小,
根据A,B,C点横坐标,可知点A,B在第三象限,C在第一象限,
﹣3<﹣1,2>0,
∴y2<y1<y3;
故选:B.
【点睛】本题考查了反比例函数的图象和性质,熟练掌握反比例函数的增减性是解题的关键.
6.(2025 吉林二模)关于x的不等式2x﹣a≤﹣1的解集如图所示,那么a的值是( )
A.﹣2 B.2 C.﹣3 D.3
【点拨】先求出不等式的解集,然后根据数轴写出不等式的解集,从而可以得到关于a的方程,再求解即可.
【解析】解:由不等式2x﹣a≤﹣1可得x≤,
由数轴可得,该不等式的解集为x≤1,
∴=1,
解得a=3,
故选:D.
【点睛】本题考查解一元一次不等式、在数轴上表示不等式的解集,解答本题的关键是明确解一元一次不等式的方法.
7.(2025 崂山区一模)某中学足球队16名队员的年龄情况如下表,则这些队员年龄的众数和中位数分别为( )
年龄(单位岁) 14 15 16 17 18
人数 2 4 5 3 2
A.15,16 B.16,16.5 C.16,16 D.17,16.5
【点拨】根据中位数、众数的意义进行计算即可.
【解析】解:足球队16名队员的年龄出现次数最多的是16岁,共出现5次,
因此众数是16岁;
将这16名队员的年龄从小到大排列,处在中间位置的两个数都是16岁,
因此中位数是16岁,
故选:C.
【点睛】本题考查中位数、众数,理解中位数、众数的意义,掌握中位数、众数的计算方法是正确解题的关键.
8.(2025 西宁一模)某环卫公司为清理卫生死角内的垃圾,调用甲车3h,只清理了一半垃圾,为了加快进步,再调用乙车,两车合作1.2h清理完另一半垃圾,设乙车单独清理全部垃圾的时间为xh,根据题意可列出方程为( )
A.+=1 B.+= C.+=1 D.+=
【点拨】首先明确将总工作量看作单位1,则甲乙合作完成的工作量=;根据甲的工作量为,乙的工作量为:,可得方程.
【解析】解:甲的工作效率为,乙的工作效率为,所以方程为:+=.
故选:B.
【点睛】本题考查分式方程的应用,找到等量关系列出方程是解题关键.
9.(2025 义乌市二模)如图,在四边形ABCD中,已知AD∥BC,∠B=90°,,对角线AC平分∠BAD,∠DCA:∠BCA=2:3,则CD的值为( )
A. B. C. D.
【点拨】根据角平分线的意义和平行线的性质可证明△ABC是等腰直角三角形,由勾股定理得AC=2,由∠DCA:∠BCA=2:3得∠ACD=30°,过点D作DE⊥AC,可证明△ADE是等腰直角三角形,设DE=AE=x,则CE=2﹣x,由可求出x的值,再根据可求出CD的长.
【解析】解:∵AD∥BC,∠B=90°,AB=,
∴∠B+∠BAD=180°,
∴∠BAD=90°,
∵AC平分∠BAD,
∴,
∵AD∥BC,
∴∠DAC=∠ACB,
∴∠BAC=∠ACB=45°,
∴,
∴,
∵∠DCA:∠BCA=2:3,
∴;
如图,过点D作DE⊥AC,
∴∠AED=90°,
∵∠DAE=45°,
∴∠ADE=∠DAE=45°,
∴AE=DE,
设DE=AE=x,则CE=2﹣x,
∵,
∴
∴,即,
∵,
∴,
故选:D.
【点睛】本题主要考查等腰直角三角形的判定与性质,平行线的性质,角平分线的性质,熟知以上知识是解题的关键.
10.(2025 滨江区一模)如图,AB,CD是⊙O的直径,AB⊥CD,点E为劣弧(不含端点)上一点,连接AE,CE,分别交OD,OB于点F,G.若⊙O的半径为1,记OF=x,BG=y,则下列代数式的值不变的是( )
A.2x﹣y B. C.2y﹣x D.
【点拨】如图,由题可得∠1=∠2=45°,,导角证明△ACF∽△GAC,则,化简即可得到,即可判断.
【解析】解:如图,连接AC
∵AB,CD是⊙O的直径,AB⊥CD,OA=OC=1,
∴∠1=∠2=45°,,
设∠OAF=α,
则∠CAF=∠1+∠OAF=45°+α,,
∴∠CAF=∠AGC,
∴△ACF∽△GAC,
∴,即,
∴(1+x)(2﹣y)=2,
∴2﹣y+2x﹣xy=2,
∴2x﹣y=xy,
两边同时除以xy得:,
故D符合题意,而A、B、C代数式的值均不能证明不变,故不符合题意,
故选:D.
【点睛】本题考查了圆周角定理,相似三角形的判定与性质,勾股定理等知识点,正确添加辅助线,熟练掌握各知识点并灵活运用是解题的关键.
二、填空题:本题共6小题,每小题3分,共18分。
11.(2024 新丰县一模)因式分解:m2﹣25= (m+5)(m﹣5) .
【点拨】原式利用平方差公式分解即可.
【解析】解:原式=(m+5)(m﹣5),
故答案为:(m+5)(m﹣5)
【点睛】此题考查了因式分解﹣运用公式法,熟练掌握平方差公式是解本题的关键.
12.(2025 上虞区二模)若分式的值为1,则字母x的取值为 2 .
【点拨】由题意易得=1,解方程后并检验即可.
【解析】解:由题意得=1,
去分母得:x+2=4,
解得:x=2,
经检验,x=2是分式方程的解,
故答案为:2.
【点睛】本题考查解分式方程,熟练掌握解方程的方法是解题的关键.
13.(2025 濠江区一模)一个袋子中有2个白球和若干个黑球,它们除了颜色外都相同,随机从中摸一个球,恰好摸到黑球的概率是,则袋子中有 3 个黑球.
【点拨】设袋子中有x个黑球,由此列式求解即可.
【解析】解:设袋子中有x个黑球,
∵随机从中摸一个球,恰好摸到黑球的概率是,
∴,
解得,x=3,
检验,当x=3时,原分式方程有意义,
∴袋子中有3个黑球,
故答案为:3.
【点睛】本题考查了概率公式,熟记概率公式熟解题的关键.
14.(2025 建邺区一模)如图,在矩形ABCD中,点A的坐标是(0,﹣1),点B的坐标是(2,0),点C在y轴上.若反比例函数的图象经过点D,则k= ﹣6 .
【点拨】根据三角形相似,可求出D点坐标,把D点坐标代入反比例函数解析式中,即可求出k的值.
【解析】
解:过点D作DE垂直于y轴,并交y轴于点E,
∠CAB+∠ABO=90°,
∠CAB+∠ACB=90°
∴∠ABO=∠ACB,
在Rt△OAB和Rt△OCB中,
∠AOB=∠COB,
∠ABO=∠ACB,
∴Rt△OAB和∽Rt△OCB,
∴=,
∵OA=1,OB=2,
∴OC=4,
∵DC∥AB,
∴∠DCA=∠CAB,
∵DC=AB,∠DCA=∠CAB,∠DEC=∠BOA,
∴△DEC=△BOA,
∴DE=OB,CE=AO,
∴D点坐标为(﹣2,3),
∴点D在反比例函数上,
∴y=,即3=,
∴k=﹣6.
故答案为:﹣6.
【点睛】本题主要考查了反比例函数的性质,熟练掌握反比例函数的性质是解题的关键.
15.(2025 济宁二模)如图,⊙O半径为,正方形ABCD内接于⊙O,点E在上运动,连接BE,作AF⊥BE,垂足为F,连接CF.则CF长的最小值为 .
【点拨】如图,取AB的中点K,以AB为直径作⊙K,想办法求出FK,CK,根据CF≥CK﹣FK即可解决问题.
【解析】解:如图,取AB的中点K,以AB为直径作⊙K,
∵AF⊥BE,
∴∠AFB=90°,
∵AK=BK,
∴KF=AK=BK,
∵正方形ABCD的外接圆的半径为,
∴AB=BC==2,
∴KF=AK=KB=1,
∵∠CBK=90°,
∴CK===,
∵CF≥CK﹣KF,
∴CF≥﹣1,
∴CF的最小值为﹣1.
故答案为﹣1.
【点睛】本题考查正多边形与圆,圆周角定理,解直角三角形等知识,解题的关键是学会用转化的思想思考问题,属于中考常考题型.
16.(2025 宣城二模)如图,正方形ABCD的边长为6,点E,F分别在BC,AD上.将该正方形沿EF折叠,使点A落在CD边上的点M处,连接AM,与折痕EF交于点P.
(1)若M是CD的中点,则AF的长为 ;
(2)若G为MN的中点,随着折痕EF位置的变化,PG+PM的最小值为 3 .
【点拨】(1)由折叠得EF是AM的中垂线,根据线段垂直平分线的性质求出AF=MF,再根据勾股定理求出AF的长.
(2)取AB的中点Q,根据两点之间线段最短得出PG+PM的最小值.
【解析】解:(1)根据折叠的性质可得EF是AM的垂直平分线,
∴AF=MF,
设AF=MF=x,则DF=6﹣x.
∵M是CD的中点,
∴DM=CD=3,
在Rt△DFM中,DF2+DM2=FM2,
即(6﹣x)2+32=x2,
解得x=,
即AF的长为,
故答案为:;
(2)如图,取AB的中点Q,连接QP,PG,PD,由折叠的对称性可知PQ=PG.
∵G为MN的中点,△ADM为直角三角形,
∴PD=AM=PM,
∴PG+PM=PQ+DP≥DQ,
当且仅当D,P,Q三点共线时PG+PM最小,最小值===3,
故答案为:
【点睛】本题考查了折叠的性质、正方形的性质、勾股定理、最值问题,第二问有难度,解题的关键是取AB的中点Q,确定PG+PM=PQ+DP,属于中考常考题型.
三.解答题(共8小题,其中第17-22题每题8分,第23题10分,第24题每题12分,共72分)
17.(2025 西宁一模)计算:.
【点拨】先计算乘方、零指数幂、特殊角的三角函数值、二次根式,再计算乘法,最后计算加减即可得出答案.
【解析】解:
=
=
=0.
【点睛】此题主要考查了实数的混合运算,熟练掌握乘方运算的法则,零指数幂的运算法则,二次根式的化简,熟记特殊角的三角函数值是解决问题的关键.
18.(2025 乾安县模拟)先化简,再求值:(2a+b)2﹣(b﹣2a)(2a+b),其中a=﹣2,b=1.
【点拨】先根据完全平方公式和平方差公式进行计算再合并同类项,最后代入求出答案即可.
【解析】解:(2a+b)2﹣(b﹣2a)(2a+b)
=(4a2+4ab+b2)﹣(b2﹣4a2)
=4a2+4ab+b2﹣b2+4a2
=8a2+4ab,
当a=﹣2,b=1时,
原式=8×(﹣2)2+4×(﹣2)×1
=8×4﹣8
=32﹣8
=24.
【点睛】本题考查了整式的化简求值,能正确根据整式的运算法则进行计算是解此题的关键,注意运算顺序.
19.(2025 泰州二模)如图,△ABC中,∠ABC为锐角,AB<BC.点E为边BC上一点,点F为平面内一点,且四边形AECF为菱形.
(1)在图1中,请利用无刻度的直尺和圆规,作出菱形AECF.(不写作法,保留作图痕迹)
(2)若AC=5,BC=8,且△ABC的面积为16,则菱形AECF的边长为 .
【点拨】(1)作线段AC的垂直平分线MN,MN交BC于点E,以C为圆心,CE为半径作弧交MN于点F,连接AF,CF,四边形AECF即为所求.
(2)过点A作AH⊥BC于点H.利用面积法求出AH,设AE=EC=x,利用勾股定理构建方程求出x即可.
【解析】解:(1)如图1中,四边形AECF即为所求;
(2)过点A作AH⊥BC于点H.
∵△ABC的面积= BC AH,
∴AH==4,
∴CH===3,
设AE=EC=x,则有x2=42+(x﹣3)2,
解得x=.
∴AE=EC=,
故答案为:.
【点睛】本题考查作图﹣复杂作图,菱形的判定和性质,勾股定理,解题的关键是理解题意,灵活运用所学知识解决问题
20.(2025 齐齐哈尔一模)2024年嫦娥六号探测器成功完成了人类历史上首次月球背面采样的壮举,2025年嫦娘七号与嫦娥八号的研制工作也将稳步向前,中国航空航天技术即将开启新的篇章.某校为了普及航空航天知识,对该校2000名学生进行了“航空航天”知识测试,
从中随机抽取了部分学生的成绩整理绘制成如下不完整的统计图表:
成绩统计表
组别 成绩x(分) 百分比
A组 x<60 5%
B组 60≤x<70 15%
C组 70≤x<80 a%
D组 80≤x<90 35%
E组 90≤x≤100 25%
根据所给信息,解答下列问题:
(1)本次调查的成绩统计表中a= 20 ;
(2)补全条形统计图;
(3)本次抽取的学生成绩的中位数落在 D 组(选填A、B、C、D或E);
(4)试估计该校2000名学生中成绩在80分以上(包括80分)的人数.
【点拨】(1)利用1减去其他四组所占的百分比即可得a的值;
(2)先根据A的条形统计图和统计表信息求出此次调查抽取的总人数,再乘以C组所占百分比可得C组的人数,据此补全条形统计图即可得;
(3)根据中位数的定义求解即可得;
(4)利用该校学生总人数乘以成绩在80分以上(包括80分)的人数所占的百分比即可得.
【解析】解:(1)利用1减去其他四组所占的百分比可得:
a%=1﹣5%﹣15%﹣35%﹣25%=20%,
∴a=20,
故答案为:20.
(2)此次调查抽取的总人数为10÷5%=200(名),
则C组的人数为200×20%=40(名),
补全条形统计图如下:
(3)∵10+30+40=80,10+30+40+70=150,
∴排在第100个数和第101个数均在D组,
∴被抽取的学生成绩的中位数落在D组,
故答案为:D.
(4)2000×(35%+25%)=1200(名),
答:估计该校1200名学生中成绩在80分以上(包括80分)的人数为1200名.
【点睛】本题考查了统计表、条形统计图、中位数、利用样本估计总体,熟练掌握统计调查的相关知识是解题关键.
21.(2025 淮安区模拟)如图,已知CD是Rt△ABC斜边AB上的中线,过点D作AC的平行线,过点C作CD的垂线,两线相交于点E.
(1)求证:△ABC∽△DEC;
(2)若AB=8,CE=3,求△ABC的周长.
【点拨】(1)先根据斜边上的中线性质得到DA=DC,则∠A=∠ACD,再根据平行线的性质得到∠ACD=∠CDE,所以∠A=∠CDE,加上∠ACB=∠DCE=90°,则根据相似三角形的判定方法可判断△ABC∽△DEC;
(2)先利用斜边上的中线性质得到CD=AB=4,再利用勾股定理计算出DE=5,接着根据相似三角形的性质得到==,然后求出AC、BC,从而得到△ABC的周长.
【解析】(1)证明:∵DC⊥CE,
∴∠DCE=90°,
∵CD是Rt△ABC斜边AB上的中线,
∴DA=DC,
∴∠A=∠ACD,
∵AC∥DE,
∴∠ACD=∠CDE,
∴∠A=∠CDE,
∵∠ACB=∠DCE,
∴△ABC∽△DEC;
(2)解:∵CD是Rt△ABC斜边AB上的中线,
∴CD=AB=4,
在Rt△DCE中,DE===5,
∵△ABC∽△DEC,
∴==,即==,
∴AC=,BC=,
∴△ABC的周长=++8=.
【点睛】本题考查了相似三角形的判定与性质:在判定两个三角形相似时,应注意利用图形中已有的公共角、公共边等隐含条件;灵活运用相似三角形的性质进行几何计算是解决问题的关键.也考查了直角三角形斜边上的中线性质.
22.(2025 西湖区二模)小敏和小慧去西湖风景区游玩,约好在少年宫广场见面.如图1,A地、B地、少年宫广场在一条直线上.小敏从A地出发,先匀速步行至车站,再坐公交车前往少年宫广场.同时,小慧从B地出发,骑车去少年宫广场,平均速度为200米/分钟.两人距离A地的路程s(米)和所经过的时间t(分)之间的函数关系如图2所示.(公交车的停车时间忽略不计)
(1)求公交车的平均速度.
(2)求同时出发后,经过多少时间小敏追上小慧.
(3)在小敏坐公交车的过程中,当她与小慧相距400米时,求t的值.
【点拨】(1)根据速度=路程÷时间计算即可;
(2)分别写出当10≤t≤30时小敏距离A地的路程s和所经过的时间t之间的函数关系式、小慧距离A地的路程s和所经过的时间t之间的函数关系式,令两函数值相等列关于t的一元一次方程并求解即可;
(3)当10≤t≤30时,令两函数值差的绝对值为400,列关于t的方程并求解即可.
【解析】解:(1)(8800﹣800)÷(30﹣10)=400(米/分).
答:公交车的平均速度是400米/分.
(2)当10≤t≤30时,小敏距离A地的路程s和所经过的时间t之间的函数关系式为s=800+400(t﹣10)=400t﹣3200,
小慧距离A地的路程s和所经过的时间t之间的函数关系式为s=200t+1800,
当小敏追上小慧时,得400t﹣3200=200t+1800,
解得t=25.
答:同时出发后,经过25分小敏追上小慧.
(3)当10≤t≤30时,得|400t﹣3200﹣(200t+1800)|=400,
解得t=23或27.
答:小敏坐公交车的过程中,当她与小慧相距400米时,求t的值为23或27.
【点睛】本题考查一次函数的应用,掌握时间、速度和路程之间的关系是解题的关键.
23.(2024 玉环市二模)已知二次函数y=ax2﹣2(a+1)x+4(a≠0).
(1)若二次函数过点(1,1)
①求二次函数的表达式;
②当y随x的增大而减小时,求x的取值范围.
(2)若点和点在该二次函数图象上,求的值.
【点拨】(1)①依据题意,由二次函数过点(1,1),从而可得1=a﹣2(a+1)+4,求出a后即可得解;
②依据题意,由①y=x2﹣4x+4=(x﹣2)2,结合二次函数的性质可以判断得解;
(2)依据题意,先求出抛物线对称轴,在根据P,Q关于对称轴对称求出n=2,再把点P坐标代入抛物线求出b=2﹣,再求出(+b)2+n2的值;
【解析】解:(1)①∵二次函数过点(1,1),
∴1=a﹣2(a+1)+4.
∴a=1.
∴二次函数的表达式为y=x2﹣4x+4.
②由①y=x2﹣4x+4=(x﹣2)2,
∴当x<2时,y随x的增大而减小.
∴当y随x的增大而减小时,x<2.
(2)∵y=ax2﹣2(a+1)x+4(a≠0),
∴抛物线对称轴为直线x=﹣=1+.
∵点P(,b)和点Q(+n,b)关于对称轴对称,
∴=1+.
∴n=2.
把P(,b)代入函数解析式得:a×﹣2(a+1)×+4=b,
解得b=2﹣.
∴(+b)2+n2=(+2﹣)2+22=8.
【点睛】本题主要考查二次函数图象与系数的关系,解题关键是掌握二次函数的性质.
24.(2025 宁波一模)已知△ABC内接于圆O,AD平分∠BAC交圆O于点D,交BC于点E,M是AD上一点.
(1)若AB=AC, ①(或②) ,求∠BDC的度数.
①AM=2ME=2DE;②∠MBC=∠MBA=2∠BAD.
(作答第(1)题时,先选择①或②填写在横线处,使题目完整,然后求解∠BDC的度数.)
(2)若AB=c,AE=m,AC=b,求DE的长.
(3)若∠MBC=∠MCA=∠MAB,求证:BC2=AB AC.
【点拨】(1)当选择①时,由题意易得AE⊥BC,BE=EC,∠BAD=∠CAD,然后可得AD是直径,则有点M是圆心,且四边形BDCM是平行四边形,进而问题可求解;若选择②,由题意易得AE⊥BC,∠BAD=∠CAD,设∠BAD=α,则有∠MBC=∠MBA=2α=∠BAC,然后可得方程2α+3α=90°,进而问题可求解;
(2)由题意易得∠BAD=∠CAD,则可证△ABD∽△AEC,则有,进而问题可求解;
(3)先证明△ABC∽△BMD,△ABC∽△MDC,则有,,然后根据BD=CD可得,进而问题可求证.
【解析】(1)解:当选择①时;
∵已知△ABC内接于圆O,AD平分∠BAC交圆O于点D,AB=AC,
∴AE⊥BC,BE=EC,∠BAD=∠CAD,
∴,
∴AD是直径,
∵AM=2ME=2DE,
∴ME=DE,AM=DM,
∴点M是圆心,且四边形BDCM是平行四边形,
∵BM=CM,
∴四边形BDCM是菱形,
∴BM=BD=DM=CD=MC,
∴△BDM,△CDM都为等边三角形,
∴∠BDM=∠CDM=60°,
∴∠BDC=120°;
若选择②;
∵已知△ABC内接于圆O,AD平分∠BAC交圆O于点D,AB=AC,
∴AE⊥BC,∠BAD=∠CAD,
由∠MBC=∠MBA=2∠BAD可设∠BAD=α,则有∠MBC=∠MBA=2α=∠BAC,
∴∠BMD=∠MBA+∠BAD=3α,
∵∠MEB=90°,
∴∠MBC+∠BME=90°,即2α+3α=90°,
∴α=18°,
∴∠BAC=2α=36°,
∵四边形ABDC内接于圆O,
∴∠BDC=180°﹣∠BAC=144°,
故答案为:①(或②);
(2)解:已知△ABC内接于圆O,AD平分∠BAC交圆O于点D,
∴∠BAD=∠CAD,
∵∠ADB=∠ACE,
∴△ABD∽△AEC,
∴,
∵AB=c,AE=m,AC=b,
∴,
∴,
∴;
(3)证明:已知△ABC内接于圆O,AD平分∠BAC交圆O于点D,
∴∠BAD=∠CAD,
∵∠MBC=∠MCA=∠MAB,
∴∠MBC=∠MCA=∠MAB=∠CAD,
∴∠BMD=∠BAM+∠ABM=∠ABM+∠MBC=∠ABC,
∵∠BDM=∠ACB,
∴△ABC∽△BMD,
∴,即,
∵∠DMC=∠CAD+∠ACM=2∠CAD,
∴∠BAC=∠DMC,
∵∠ABC=∠MDC,
∴△ABC∽△MDC,
∴,
∴,
∵∠BAD=∠CAD,
∴,
∴BD=CD,
∴,
∴,
∴BC2=AB AC.
【点睛】本题属于圆的综合题,主要考查垂径定理、菱形的性质与判定、圆周角的性质、圆内接四边形的性质及相似三角形的性质与判定,熟练掌握垂径定理、菱形的性质与判定、圆周角的性质、圆内接四边形的性质及相似三角形的性质与判定是解题的关键.
21世纪教育网 www.21cnjy.com 精品试卷·第 2 页 (共 2 页)
HYPERLINK "http://21世纪教育网(www.21cnjy.com)
" 21世纪教育网(www.21cnjy.com)
同课章节目录
