2025年中考数学二轮复习专题4角的数量关系问题(含答案)
文档属性
| 名称 | 2025年中考数学二轮复习专题4角的数量关系问题(含答案) |  | |
| 格式 | docx | ||
| 文件大小 | 390.3KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 通用版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2025-05-29 13:42:57 | ||
图片预览



文档简介
专题4角的数量关系问题
核心归纳
编写说明:将此类难题的核心要点总结、结合例题加深理解,之后练综合题目易有解题思路.
类型 何时用 辅助线方法及核心 常用结论
二倍角问题 题 目 中出 现 2倍角 角平分线法:作二倍角的平分线,为得到相等的角. 条件:∠AOB=2∠CO'D、 辅助线:作OE 平分∠AOB、 得到等角:∠AOE=∠BOE=∠CO'D.
加倍法:加倍半角,为得到相等的角. 条件:∠AOB=2∠CO'D. 辅助线:作 得到等角:∠DO'E=∠AOB.
等腰法:由二倍角关系,构造以二倍角邻补角为顶角或一倍角为底角的等腰三角形,从而得到等角. 条件:∠B=2∠C. 辅助线1:作 BD 平分∠ABC. 辅助线2:作∠CAD=∠C. 辅助线3:延长CB 至点D,使DB=AB. 得到等角: 辅助线1: ∠ABD= ∠DBC=∠C. 辅助线2: ∠ABD= ∠ADB. 辅助线3: ∠D=∠C.
绝 配 角问题(若两 个 角满足α+2β =180°,则称 a,β为一 组绝配角) 条 件 中出 现 绝配 角 或者 导角后 得到绝 配角 两个角α,β共顶点 2α+β=180° 反向延长OB. 得到等角:∠AOD=∠AOC=α.
反向延长OA. 得到等角:∠BOD=∠AOC=α.
两个角α,β不共顶点 2a+β=180° 以α为底角构造等腰三角形. 得到等角:∠ACB=β.
以β为顶角构造等腰三角形. 得到等角: ∠E= ∠DFE=α.
类型突破
编写说明:每类例题由浅入深设置,包含该类型的经典情况且在不同几何图形背景下,让学生先练透每个类型,抓住核心本质后再综合练习.
类型1·二倍角问题
例1.如图,在△ABC 中、AB=3,AC=4,∠B=2∠C,求 BC 的长.(请用三种方法解答)
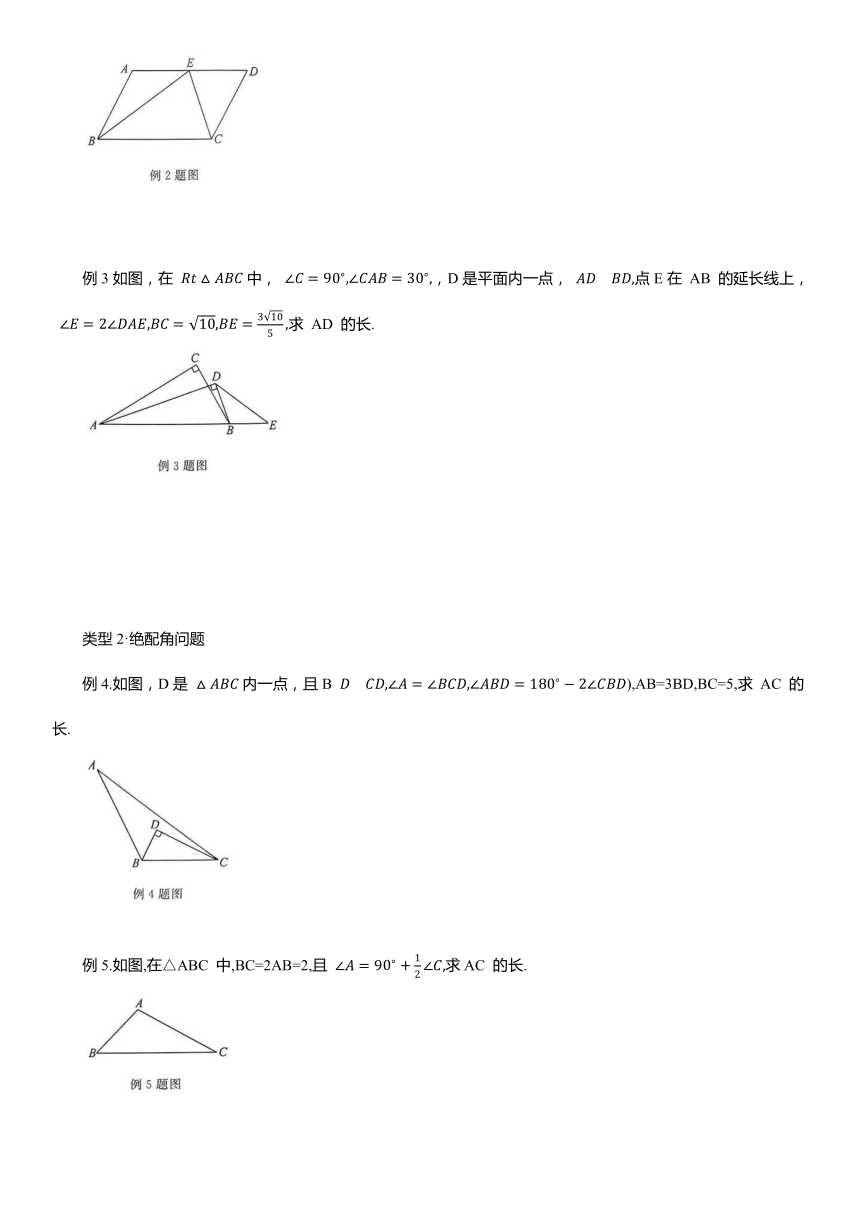
例2.如图.在 中、E是 A D的中点,连接BE,CE,若. 2∠AEB,求AB 的长.
例3如图,在 中, ,D是平面内一点, 点E在 AB 的延长线上, 求 AD 的长.
类型2·绝配角问题
例4.如图,D是 内一点,且B ),AB=3BD,BC=5,求 AC 的长.
例5.如图,在△ABC 中,BC=2AB=2,且 求AC 的长.
例6.如图,在 Rt△ABC 中,. D 是 BC上方一点,且. 180°,AB+BD=2AC,点 E 在 BC 上,. ,射线 CF 与 DE 的延长线相交于点 F,且∠BCF=∠ACB,若DF=4,BC=3,求CF 的长.
综合提升练
1.在△ABC 中.
(1)如图1,求证:AB=AC;
(2)如图2,延长CD至点E,使CE=AC,连接AE 并延长,交CB 的延长线于点F,连接EB,当EB⊥BC 时,探究 BC 和EF 之间的数量关系,并证明;
(3)如图3,将(2)中的“EB⊥BC”改为“EB⊥AF”,其他条件不变.
①求证:BC=BF;
若BC=2,求 AE 的长.
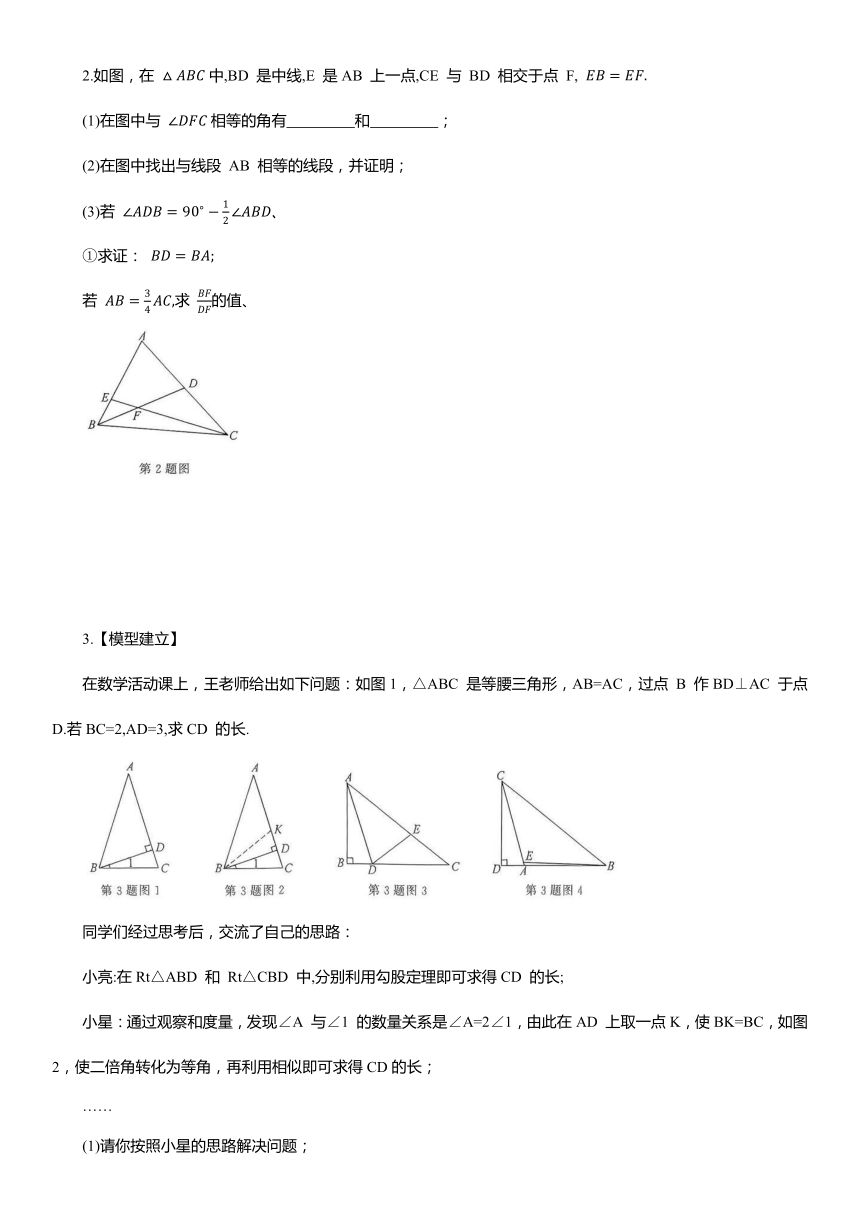
2.如图,在 中,BD 是中线,E 是AB 上一点,CE 与 BD 相交于点 F,
(1)在图中与 相等的角有 和 ;
(2)在图中找出与线段 AB 相等的线段,并证明;
(3)若
①求证:
若 求 的值、
3.【模型建立】
在数学活动课上,王老师给出如下问题:如图1,△ABC 是等腰三角形,AB=AC,过点 B 作BD⊥AC 于点D.若BC=2,AD=3,求CD 的长.
同学们经过思考后,交流了自己的思路:
小亮:在Rt△ABD 和 Rt△CBD 中,分别利用勾股定理即可求得CD 的长;
小星:通过观察和度量,发现∠A 与∠1 的数量关系是∠A=2∠1,由此在AD 上取一点K,使BK=BC,如图2,使二倍角转化为等角,再利用相似即可求得CD的长;
……
(1)请你按照小星的思路解决问题;
【模型应用】
小星的思路运用了转化思想.王老师为了帮助学生更好地感悟转化思想,将图1进行了变换,并提出下面的问题:
(2)如图3,在 Rt△ABC 中,∠ABC=90°,∠C=2∠DAB,点 E 在边AC 上,且DE=CE,若AB=CD=6.求AE 的长;
【模型迁移】
(3)如图4,△ABC 是等腰三角形,AB=AC,CD⊥AB 交BA 的延长线于点 D,E 是边AC 上一点, 求 BC 的长.
4.2024辽宁模拟【模型建立】
如图1,点O在直线AB 上,射线OC,OD 位于直线AB 两侧,若∠1=∠2,则称∠1,∠2是关于直线 AB 的对称角.
当射线OC,OD 位于直线AB 同侧且∠1=∠2时,可以通过作对顶角构造出对称角,可以反向延长射线OC,得到∠2=∠3(如图 2),或者反向延长射线OD,得到∠1=∠3(如图3).
【模型应用】
(1)小明受到模型启发,运用两种方法构造出对称角解决了下面的问题:
如图4,点C,D均在AB上,点E,F 在直线AB 外,连接CE,CF,DE,DF,DE 与CF 相交于点O.若∠FDB=∠EDA=45°,EC=CF,求∠ECF 的度数.
方法一:延长ED 至点 H,使DH=DF,连接CH.
方法二:延长FD 至点H,使DH=DE,连接CH.
请你依照小明的解题思路,任选一种方法,写出证明过程;
(2)小明又尝试将(1)中问题进行变式提出了新问题,请你应用“对称角”模型构造全等三角形或者按照自己的解题思路解答.
如图5,在Rt△ABC中,∠BAC=90°,D 是BC的中点,点E,F 分别在AC,BC上,∠AFB=∠CFE,∠AED=∠CEF,猜想 AF,EF 与DE 之间的数量关系,并说明理由;
【学以致用】
(3)如图6,在四边形 ABCD 中, AC,BD 相交于点 E,且∠BEC=60°,若AD=5,BD=15,求 AC 的长.
5.在四边形ABCD 中,,
(1)如图1,当四边形 ABCD 是平行四边形时,求 BD 的长;
(2)如图2.当 时,求 BC 的长;
(3)如图3,当∠BAD+∠BCD=180°,AB=AD 时,直接写出 BC 的长.
专题4 角的数量关系问题
例1.解:方法1:如图1,作∠ABC 的平分线 BD 交AC 于点 D.
∴∠ABC=2∠ABD=2∠DBC.
∵∠ABC=2∠C,∴∠ABD=∠DBC=∠C.
∴BD=CD.
∵∠A=∠A,∠ABD=∠C,∴△ABD∽△ACB.
方法2:如图2,以点C 为顶点,作∠BCD=∠ACB,交AB 的延长线于点D.
∴∠ACD=2∠ACB=2∠BCD.
∵∠ABC=2∠ACB,∠ABC=∠BCD+∠D,
∴∠ABC=∠ACD,∠ACB=∠D=∠BCD.
∴△ACB∽△ADC,BC=BD.
即
方法3:如图3,延长CB 至点 D,使BD=AB,连接AD.
∴BD=AB=3,∠BAD=∠D.
∵∠ABC=∠BAD+∠D=2∠D,∠ABC=2∠C,
∴∠BAD=∠D=∠C.
∴AC=AD=4,△BAD∽△ACD.
例2.解:如图,在 BC 上取一点 F,使 BF=EF,过点 E 作EH⊥BC于点 H,过点C 作CG⊥AD 于点G.
∴∠EBF=∠BEF,∠EHC=∠CGE=∠CGD=90°.
∴∠EFC=∠EBF+∠BEF=2∠EBF.
∵四边形ABCD是平行四边形,
∴AD∥BC,AD=BC=5,AB=DC.
∴∠AEB =∠EBF,∠DEC = ∠ECF,EH = CG,∠HCG=∠DGC=90°.
∴四边形 EHCG 是矩形.∴CH=EG.
∵∠DEC=2∠AEB,∴∠ECF=2∠EBF=∠EFC.
∴BF=EF=EC.∴FH=CH= CF.
设BF=EF=EC=x,则(CF=5-x.
在Rt△EBH 和 Rt△EFH 中、∵由勾股定理,
解得x=3(负值已舍).
∴BF=EF=EC=3,EG=CH=FH=1,CG=EH=2
∵E 为AD 的中点,
∴ 根 据 勾 股 定 理、得
例3.解:如图,在AB 上取一点M,使AM=DM,过点 D 作DN⊥AE 于点N.
∴∠DAE=∠ADM.
∴∠DME=∠DAE+∠ADM=2∠DAE.
∵∠E=2∠DAE,∴∠E=∠DME.
∴DM=DE.∵DN⊥AE,∴MN=EN= ME.
∵AD⊥BD,∴∠ADB=90°.
∴∠MDB=90°-∠ADM,∠DBM=90°-∠DAE.
∴∠MDB=∠DBM.∴MD=MB=AM.
∵在 Rt△ABC 中,∠CAB=30°,BC=
在 Rt△MDN 中,根据勾股定理,得
∴在 Rt△ADN 中,根据勾股定理,得
例4.解:如图,在AB的延长线上取点E,使BE=BD,连接CE.
∵∠ABD=180°-2∠CBD,∴∠ABC=180°-∠CBD.
又∠ABC=180°-∠CBE,∴∠CBD=∠CBE.
又BD=BE,BC=BC,∴△BCD≌△BCE.
∴∠BCD=∠BCE=∠A,∠E=∠D=90°.
又∠E=∠E,∴△BCE∽△CAE.∴EE=CEE.
∵AB=3BD,BD=BE,∴AE=4BE.
,即CE=2BE.
在 Rt△BCE中,∵根据勾股定理,
∴根据勾股定理,得
例5.解:如图,在CA 的延长线上取一点D,使BD=BA,连接BD.∴∠D=∠DAB.∴∠DBA=180°-2∠DAB=180°-2(180°-∠BAC)=2∠BAC-180°.
又∠D=∠D,∴△DBA∽△DCB.∴DBC=ABD=ABC.
例6.解:如图,延长DB,CF 相交于点G,延长 BG 至点 H,使BH=BC,连接CH.
∵∠ABD+2∠ABC=180°,∠ABD+∠ABC+∠GBC=180°,∴∠ABC=∠GBC.
又BC=BC,∠ACB=∠GCB,∴△ABC≌△GBC.
∴AB=GB,AC=GC,∠A=∠BGC=90°.∴∠CGH=90°.
∵AB+BD=2AC,∴BD+BG=2GC,即DG=2GC.设∠ABC=∠GBC=α.
∵BD=BE,BC=BH=3,
又∠CGH=∠DGF,∴△GCH∽△GDF.
∴GF=2GH,CH=2.
∵在 Rt△BCG 和 Rt△HCG 中,根据勾股定理,CG
1.解:(1)证明:∵CD⊥AB,∴∠BDC=90°.
∴AB=AC.
证明:如图1,过点 A 作AJ⊥BC 于点J.
又AB=AC,
设∠BAC=α,则
∵EB⊥BC,∴∠EBF=∠EBC=90°=∠CJA.
又∠BCE=∠CAJ,CE=AC,∴△CBE≌△AJC.
∴∠F=45°.
在 Rt△BEF 中,
即
(3)①如图2,过点 E 作EK⊥BF于点K.
由(2)可知,∠F=45°,BC=2EK.
∵BE⊥EF,∴∠BEF=90°.
∴∠EBF=45°=∠F.∴EF=EB.
∴△BEF 是等腰直角三角形.
∵EK⊥FB,∴BF=2EK.∴BC=BF.
②如图2,过点 C作CR⊥AF 于点R.
∴∠CRE=90°.
又CA=CE,∴AE=2ER.
∵∠BEF=∠CRE=90°,∴BE∥CR.
又BF=CB,∴EF=ER.∴AE=2EF.
∵在 Rt△BEF 中,
2.解:(1)∠EFB;∠EBF 点拨∵EB =EF,∴∠EBF =∠EFB=∠DFC.
(2)CF=AB.
证明:如图1,延长BD到点G,使BD=GD,连接CG.
∵BD 是△ABC的中线,∴AD=CD.
又∠ADB=∠CDG,BD=GD,∴△ABD≌△CGD.
∴AB=CG,∠ABD=∠G.
由(1),知∠GFC=∠EBF.
∴∠GFC=∠G.∴CF=CG.∴CF=AB.
一题多解如图2,在 BD的延长线上取一点 H,使CD=CH.
∴∠H=∠CDH=∠ADB.
∵BD 是△ABC 的中线,∴AD=CD=CH.
由(1),知∠ABD=∠HFC.
又AD=CH,∠ADB=∠H,
∴△ABD≌△CFH.∴AB=CF.
(3)①证明:设∠ABD=α.
∴∠BAD = 180°- ∠ABD-∠ADB = 180° - α -
∴∠ADB=∠BAD.∴BD=BA.
②如图3,在 FD的延长线上取一点 M,使 FM=FC,连接CM.
∴∠M=∠MCF.
由①,知BD=AB,∠BAD=∠ADB.
∵∠MFC=∠ABD,
∴∠M=∠MCF=∠ADB=∠BAD.
∵∠ADB=∠MDC,∴∠M=∠MDC.
∴CM=CD=AD.
设CM=CD=AD=a,则AC=2a.
∵CF=AB,∴CF=FM=AB=BD.∴DM=BF.
∵∠BAD=∠ADB=∠CDM=∠M、∴△ABD∽△DCM.
3.解:(1)如图1,在AD 上取一点K,使BK=BC.
∵BD⊥AC,BK=BC,
∴∠BDC=90°,∠1=∠KBD,CD=KD.
∴∠C=90°-∠1,∠CBK=2∠1.
∵AB=AC,∴∠ABC=∠C=90°-∠1.
∴∠A=180°-∠ABC-∠C=2∠1=∠CBK.
又∠C=∠C,∴△CBK∽△CAB.
负值已舍).
(2)如图2,延长CB到点G,使BD=BG,连接AG,过点 A作AF⊥DE于点F.
∵∠ABC=90°,∴AB⊥BD.
又BD=BG,∴AG=AD.
∴∠DAG=2∠DAB,∠G=∠ADG.
又∠C=2∠DAB,∴∠DAG=∠C.
又∠G=∠G,∴△AGD∽△CGA.
∴∠ADG=∠CAG.∴∠G=∠CAG.∴AC=GC.
设BD=x,则 BG=x.
∵CD=6,∴AC=GC=6+2x,BC=6+x.
在 Rt△ABC中,根据勾股定理,
解得x=2(负值已舍).
∴AC=6+2x=10,BD=DG=2.
设∠C=2∠DAB=2α,则∠DAB=α.
∵∠ABC=90°,∴∠ADB=90°-α.
∵DE=CE,∴∠EDC=∠C=2α.
∴∠ADE=180°-∠ADB-∠EDC=90°-α=∠ADB.
∵AF⊥DE,∴∠AFD=90°=∠ABD.
又AD=AD,∠ADB=∠ADF,∴△ADB≌△ADF.
∴AB=AF=6,BD=FD=2.
设EF=y,则DE=CE=2+y.
∴AE=AC-CE=10-(2+y)=8-y.
在Rt△AFE 中,根据勾股定理,
解得
(3)如图3,延长CA 至点G,使BE=BG,过点 B 作BF⊥EG于点F.
∴EF=GF.
设∠ACB=2α,则
∵BE=BG,∴∠BEA=∠G=90°-α.
∴∠EBG=180°-∠BEA-∠G=2α=∠ACB.
又∠G=∠G,∴△EBG∽△BCG.
∴∠BEG=∠CBG.∴∠G=∠CBG.∴CB=CG.
∵CD⊥AB,BF⊥EG,∴∠D=∠BFA=90°.
又∠CAD=∠BAF,AC=AB,
∴△CAD≌△BAF.∴AD=AF=7.
∵AE=1,∴GF=EF=AF+AE=7+1=8.
设AC=x,则AB=x,BC=CG=AC+AF+GF=x+7+8=x+15,BD=AB+AD=x+7.
在Rt△ACD和Rt△BCD 中,根据勾股定理,
即 7) .解得x=25(负值已舍).
∴BC=25+15=40.
4.解:(1)选择方法一.
如图1,延长ED 至点H,使DH=DF,连接CH.
∵∠FDB =∠EDA =45°,∴∠BDH =∠EDA =45°,∠EDF=180°-∠EDF=180°-∠EDA=90°.
又CD=CD、DF=DH,∴△FDC≌△HDC.
∴CH=CF,∠F=∠H.
∵EC=CF,∴EC=CH.∴∠E=∠H.∴∠E=∠F.
∵∠EOC=∠FOD,∴∠ECF=∠EDF=90°.
一题多解选择方法二.
如图2,延长FD 至点H,使DH=DE,连接CH.
∵∠FDB=∠EDA =45°,∴∠CDH=∠FDB=45°=∠EDA,∠EDF=180°-∠EDA-∠FDB=90°.
又CD=CD,DE=DH,∴△EDC≌△HDC.
∴EC=HC,∠E=∠H.
∵EC=CF,∴CF=HC.∴∠F=∠H=∠E.
∵∠EOC=∠FOD,∴∠ECF=∠EDF=90°.
(2)AF=EF+DE.理由如下:
如图3,延长FE 至点H,使HE=DE,连接AH,AD.
∵∠AED=∠CEF,∠CEF=∠AEH,
∴∠AED=∠AEH.
又DE=HE,AE=AE,∴△AED≌△AEH.
∴∠HAE=∠DAE.
∵在 Rt△ABC 中,∠BAC=90°,D 是BC 的中点.
∴AD=CD.∴∠C=∠DAE=∠HAE.∴AH∥CB.
∴∠H=∠CFE=∠AFB=∠HAF.∴AF=HF.
∵HF=EF+EH,∴AF=EF+DE.
(3)如图4,延长 DA 至点F,使AF=AC,过点 F 作FG⊥DB 于点G,连接BF.
∠BAC.
又AF=AC,AB=AB,∴△ABF≌△ABC.∴BF=BC.
又AD∥BC,∴∠BAF=∠ABC=∠ABF.
∴BF=AF=AC=BC.∴四边形ACBF 是菱形.
∴BF∥AC.∴∠FBG=∠BEC=60°.
∵FG⊥BD,∴∠FGB=∠FGD=90°.∴∠BFG=30°.
设AC=BC=BF=AF=x,则
在 Rt△BFG 中,根据勾股定理,得
∵AD=5,BD=15,∴DF=5+x,DG=15- x.
在 Rt△FDG 中,根据勾股定理,
5.解:(1)如图1,在 BD 上取一点E,使BE=CE,过点 C 作CF⊥BD 于点 F.
∴∠CBD=∠ECB,∠EFC=90°.
∴∠DEC=2∠CBD=2∠ECB.
∵∠ABD=2∠CBD,∴∠DEC=∠ABD.
∵四边形ABCD 是平行四边形,
∴∠EDC=∠ABD.∴∠DEC=∠EDC.
∴CD=CE=BE=5.∴EF=DF.
∵在 Rt△BFC 和 Rt△EFC 中,根据勾股定理,
即
∴DF=EF=4.∴BD=BE+EF+DF=5+4+4=13.
一题多解如图2,在 DB 的延长线上取一点E,使BE=AB,过点A 作AF⊥BD于点F.
∴∠E=∠EAB,∠AFB=90°.
∴∠ABD=2∠E=2∠EAB.
∵∠ABD=2∠CBD,∴∠E=∠CBD.
∵四边形 ABCD 是平行四边形,
∴CD=AB=BE=5,AD∥BC.∴∠ADB=∠CBD.
∴∠ADB=∠E.∴AD=AE=3
∵AF⊥BD,∴EF=DF.
∵在 Rt△BFA 和 Rt△EFA 中,根据勾股定理, 即
∴BF=4.∴DF=EF=5+4=9.
∴BD=BF+DF=4+9=13.
(2)如图3,过点D作DM∥BC,交AB 于点M,DN∥AB交BC 于点 N,DH⊥BC 于点 H.
∴四边形 BNDM 是平行四边形、∠AMD =∠ABC、∠ABC=∠DNC.
∵∠A=∠C=∠ABC,∴∠A=∠AMD、∠C=∠DNC、
∵DH⊥BC,∴NH=CH.
由(1),得BD=13.
∵在 Rt△BDH 和 Rt△NDH 中.根据勾股定理,
即
(3)BC 的长为
详解如图4,延长CB 至点 Q,使 BQ=DC,过点 A 作AP⊥BC 于点 P,连接AQ,AC.
∴∠APQ=90°.
∵∠BAD+∠BCD=180°,∠BAD+∠BCD+∠ADC+∠ABC=360°,∴∠ADC+∠ABC=180°.
又∠ABQ+∠ABC=180°,∴∠ADC=∠ABQ.
又AD=AB,DC=BQ,∴△ADC≌△ABQ.
∴AC=AQ,∠CAD=∠QAB.∴∠QAC=∠BAD.
∵AP⊥BC,∴PQ=PC,∠QAP=∠CAP.
设∠CBD=a.
∵AB=AD,∠ABD=2∠CBD,∴∠ADB=∠ABD=2a.
∴∠CAD=∠QAB=∠QAP-∠BAP=a,∠ACD=∠Q=90°-∠QAP=2a.∴∠ACD=2∠CAD.
在AC上取一点G,使AG=DG,过点 D 作 DK⊥AC 于点 K.
同理(1)可得,AQ=AC=13.
∵在 Rt△APQ 和 Rt△APB 中,根据勾股定理,
即
核心归纳
编写说明:将此类难题的核心要点总结、结合例题加深理解,之后练综合题目易有解题思路.
类型 何时用 辅助线方法及核心 常用结论
二倍角问题 题 目 中出 现 2倍角 角平分线法:作二倍角的平分线,为得到相等的角. 条件:∠AOB=2∠CO'D、 辅助线:作OE 平分∠AOB、 得到等角:∠AOE=∠BOE=∠CO'D.
加倍法:加倍半角,为得到相等的角. 条件:∠AOB=2∠CO'D. 辅助线:作 得到等角:∠DO'E=∠AOB.
等腰法:由二倍角关系,构造以二倍角邻补角为顶角或一倍角为底角的等腰三角形,从而得到等角. 条件:∠B=2∠C. 辅助线1:作 BD 平分∠ABC. 辅助线2:作∠CAD=∠C. 辅助线3:延长CB 至点D,使DB=AB. 得到等角: 辅助线1: ∠ABD= ∠DBC=∠C. 辅助线2: ∠ABD= ∠ADB. 辅助线3: ∠D=∠C.
绝 配 角问题(若两 个 角满足α+2β =180°,则称 a,β为一 组绝配角) 条 件 中出 现 绝配 角 或者 导角后 得到绝 配角 两个角α,β共顶点 2α+β=180° 反向延长OB. 得到等角:∠AOD=∠AOC=α.
反向延长OA. 得到等角:∠BOD=∠AOC=α.
两个角α,β不共顶点 2a+β=180° 以α为底角构造等腰三角形. 得到等角:∠ACB=β.
以β为顶角构造等腰三角形. 得到等角: ∠E= ∠DFE=α.
类型突破
编写说明:每类例题由浅入深设置,包含该类型的经典情况且在不同几何图形背景下,让学生先练透每个类型,抓住核心本质后再综合练习.
类型1·二倍角问题
例1.如图,在△ABC 中、AB=3,AC=4,∠B=2∠C,求 BC 的长.(请用三种方法解答)
例2.如图.在 中、E是 A D的中点,连接BE,CE,若. 2∠AEB,求AB 的长.
例3如图,在 中, ,D是平面内一点, 点E在 AB 的延长线上, 求 AD 的长.
类型2·绝配角问题
例4.如图,D是 内一点,且B ),AB=3BD,BC=5,求 AC 的长.
例5.如图,在△ABC 中,BC=2AB=2,且 求AC 的长.
例6.如图,在 Rt△ABC 中,. D 是 BC上方一点,且. 180°,AB+BD=2AC,点 E 在 BC 上,. ,射线 CF 与 DE 的延长线相交于点 F,且∠BCF=∠ACB,若DF=4,BC=3,求CF 的长.
综合提升练
1.在△ABC 中.
(1)如图1,求证:AB=AC;
(2)如图2,延长CD至点E,使CE=AC,连接AE 并延长,交CB 的延长线于点F,连接EB,当EB⊥BC 时,探究 BC 和EF 之间的数量关系,并证明;
(3)如图3,将(2)中的“EB⊥BC”改为“EB⊥AF”,其他条件不变.
①求证:BC=BF;
若BC=2,求 AE 的长.
2.如图,在 中,BD 是中线,E 是AB 上一点,CE 与 BD 相交于点 F,
(1)在图中与 相等的角有 和 ;
(2)在图中找出与线段 AB 相等的线段,并证明;
(3)若
①求证:
若 求 的值、
3.【模型建立】
在数学活动课上,王老师给出如下问题:如图1,△ABC 是等腰三角形,AB=AC,过点 B 作BD⊥AC 于点D.若BC=2,AD=3,求CD 的长.
同学们经过思考后,交流了自己的思路:
小亮:在Rt△ABD 和 Rt△CBD 中,分别利用勾股定理即可求得CD 的长;
小星:通过观察和度量,发现∠A 与∠1 的数量关系是∠A=2∠1,由此在AD 上取一点K,使BK=BC,如图2,使二倍角转化为等角,再利用相似即可求得CD的长;
……
(1)请你按照小星的思路解决问题;
【模型应用】
小星的思路运用了转化思想.王老师为了帮助学生更好地感悟转化思想,将图1进行了变换,并提出下面的问题:
(2)如图3,在 Rt△ABC 中,∠ABC=90°,∠C=2∠DAB,点 E 在边AC 上,且DE=CE,若AB=CD=6.求AE 的长;
【模型迁移】
(3)如图4,△ABC 是等腰三角形,AB=AC,CD⊥AB 交BA 的延长线于点 D,E 是边AC 上一点, 求 BC 的长.
4.2024辽宁模拟【模型建立】
如图1,点O在直线AB 上,射线OC,OD 位于直线AB 两侧,若∠1=∠2,则称∠1,∠2是关于直线 AB 的对称角.
当射线OC,OD 位于直线AB 同侧且∠1=∠2时,可以通过作对顶角构造出对称角,可以反向延长射线OC,得到∠2=∠3(如图 2),或者反向延长射线OD,得到∠1=∠3(如图3).
【模型应用】
(1)小明受到模型启发,运用两种方法构造出对称角解决了下面的问题:
如图4,点C,D均在AB上,点E,F 在直线AB 外,连接CE,CF,DE,DF,DE 与CF 相交于点O.若∠FDB=∠EDA=45°,EC=CF,求∠ECF 的度数.
方法一:延长ED 至点 H,使DH=DF,连接CH.
方法二:延长FD 至点H,使DH=DE,连接CH.
请你依照小明的解题思路,任选一种方法,写出证明过程;
(2)小明又尝试将(1)中问题进行变式提出了新问题,请你应用“对称角”模型构造全等三角形或者按照自己的解题思路解答.
如图5,在Rt△ABC中,∠BAC=90°,D 是BC的中点,点E,F 分别在AC,BC上,∠AFB=∠CFE,∠AED=∠CEF,猜想 AF,EF 与DE 之间的数量关系,并说明理由;
【学以致用】
(3)如图6,在四边形 ABCD 中, AC,BD 相交于点 E,且∠BEC=60°,若AD=5,BD=15,求 AC 的长.
5.在四边形ABCD 中,,
(1)如图1,当四边形 ABCD 是平行四边形时,求 BD 的长;
(2)如图2.当 时,求 BC 的长;
(3)如图3,当∠BAD+∠BCD=180°,AB=AD 时,直接写出 BC 的长.
专题4 角的数量关系问题
例1.解:方法1:如图1,作∠ABC 的平分线 BD 交AC 于点 D.
∴∠ABC=2∠ABD=2∠DBC.
∵∠ABC=2∠C,∴∠ABD=∠DBC=∠C.
∴BD=CD.
∵∠A=∠A,∠ABD=∠C,∴△ABD∽△ACB.
方法2:如图2,以点C 为顶点,作∠BCD=∠ACB,交AB 的延长线于点D.
∴∠ACD=2∠ACB=2∠BCD.
∵∠ABC=2∠ACB,∠ABC=∠BCD+∠D,
∴∠ABC=∠ACD,∠ACB=∠D=∠BCD.
∴△ACB∽△ADC,BC=BD.
即
方法3:如图3,延长CB 至点 D,使BD=AB,连接AD.
∴BD=AB=3,∠BAD=∠D.
∵∠ABC=∠BAD+∠D=2∠D,∠ABC=2∠C,
∴∠BAD=∠D=∠C.
∴AC=AD=4,△BAD∽△ACD.
例2.解:如图,在 BC 上取一点 F,使 BF=EF,过点 E 作EH⊥BC于点 H,过点C 作CG⊥AD 于点G.
∴∠EBF=∠BEF,∠EHC=∠CGE=∠CGD=90°.
∴∠EFC=∠EBF+∠BEF=2∠EBF.
∵四边形ABCD是平行四边形,
∴AD∥BC,AD=BC=5,AB=DC.
∴∠AEB =∠EBF,∠DEC = ∠ECF,EH = CG,∠HCG=∠DGC=90°.
∴四边形 EHCG 是矩形.∴CH=EG.
∵∠DEC=2∠AEB,∴∠ECF=2∠EBF=∠EFC.
∴BF=EF=EC.∴FH=CH= CF.
设BF=EF=EC=x,则(CF=5-x.
在Rt△EBH 和 Rt△EFH 中、∵由勾股定理,
解得x=3(负值已舍).
∴BF=EF=EC=3,EG=CH=FH=1,CG=EH=2
∵E 为AD 的中点,
∴ 根 据 勾 股 定 理、得
例3.解:如图,在AB 上取一点M,使AM=DM,过点 D 作DN⊥AE 于点N.
∴∠DAE=∠ADM.
∴∠DME=∠DAE+∠ADM=2∠DAE.
∵∠E=2∠DAE,∴∠E=∠DME.
∴DM=DE.∵DN⊥AE,∴MN=EN= ME.
∵AD⊥BD,∴∠ADB=90°.
∴∠MDB=90°-∠ADM,∠DBM=90°-∠DAE.
∴∠MDB=∠DBM.∴MD=MB=AM.
∵在 Rt△ABC 中,∠CAB=30°,BC=
在 Rt△MDN 中,根据勾股定理,得
∴在 Rt△ADN 中,根据勾股定理,得
例4.解:如图,在AB的延长线上取点E,使BE=BD,连接CE.
∵∠ABD=180°-2∠CBD,∴∠ABC=180°-∠CBD.
又∠ABC=180°-∠CBE,∴∠CBD=∠CBE.
又BD=BE,BC=BC,∴△BCD≌△BCE.
∴∠BCD=∠BCE=∠A,∠E=∠D=90°.
又∠E=∠E,∴△BCE∽△CAE.∴EE=CEE.
∵AB=3BD,BD=BE,∴AE=4BE.
,即CE=2BE.
在 Rt△BCE中,∵根据勾股定理,
∴根据勾股定理,得
例5.解:如图,在CA 的延长线上取一点D,使BD=BA,连接BD.∴∠D=∠DAB.∴∠DBA=180°-2∠DAB=180°-2(180°-∠BAC)=2∠BAC-180°.
又∠D=∠D,∴△DBA∽△DCB.∴DBC=ABD=ABC.
例6.解:如图,延长DB,CF 相交于点G,延长 BG 至点 H,使BH=BC,连接CH.
∵∠ABD+2∠ABC=180°,∠ABD+∠ABC+∠GBC=180°,∴∠ABC=∠GBC.
又BC=BC,∠ACB=∠GCB,∴△ABC≌△GBC.
∴AB=GB,AC=GC,∠A=∠BGC=90°.∴∠CGH=90°.
∵AB+BD=2AC,∴BD+BG=2GC,即DG=2GC.设∠ABC=∠GBC=α.
∵BD=BE,BC=BH=3,
又∠CGH=∠DGF,∴△GCH∽△GDF.
∴GF=2GH,CH=2.
∵在 Rt△BCG 和 Rt△HCG 中,根据勾股定理,CG
1.解:(1)证明:∵CD⊥AB,∴∠BDC=90°.
∴AB=AC.
证明:如图1,过点 A 作AJ⊥BC 于点J.
又AB=AC,
设∠BAC=α,则
∵EB⊥BC,∴∠EBF=∠EBC=90°=∠CJA.
又∠BCE=∠CAJ,CE=AC,∴△CBE≌△AJC.
∴∠F=45°.
在 Rt△BEF 中,
即
(3)①如图2,过点 E 作EK⊥BF于点K.
由(2)可知,∠F=45°,BC=2EK.
∵BE⊥EF,∴∠BEF=90°.
∴∠EBF=45°=∠F.∴EF=EB.
∴△BEF 是等腰直角三角形.
∵EK⊥FB,∴BF=2EK.∴BC=BF.
②如图2,过点 C作CR⊥AF 于点R.
∴∠CRE=90°.
又CA=CE,∴AE=2ER.
∵∠BEF=∠CRE=90°,∴BE∥CR.
又BF=CB,∴EF=ER.∴AE=2EF.
∵在 Rt△BEF 中,
2.解:(1)∠EFB;∠EBF 点拨∵EB =EF,∴∠EBF =∠EFB=∠DFC.
(2)CF=AB.
证明:如图1,延长BD到点G,使BD=GD,连接CG.
∵BD 是△ABC的中线,∴AD=CD.
又∠ADB=∠CDG,BD=GD,∴△ABD≌△CGD.
∴AB=CG,∠ABD=∠G.
由(1),知∠GFC=∠EBF.
∴∠GFC=∠G.∴CF=CG.∴CF=AB.
一题多解如图2,在 BD的延长线上取一点 H,使CD=CH.
∴∠H=∠CDH=∠ADB.
∵BD 是△ABC 的中线,∴AD=CD=CH.
由(1),知∠ABD=∠HFC.
又AD=CH,∠ADB=∠H,
∴△ABD≌△CFH.∴AB=CF.
(3)①证明:设∠ABD=α.
∴∠BAD = 180°- ∠ABD-∠ADB = 180° - α -
∴∠ADB=∠BAD.∴BD=BA.
②如图3,在 FD的延长线上取一点 M,使 FM=FC,连接CM.
∴∠M=∠MCF.
由①,知BD=AB,∠BAD=∠ADB.
∵∠MFC=∠ABD,
∴∠M=∠MCF=∠ADB=∠BAD.
∵∠ADB=∠MDC,∴∠M=∠MDC.
∴CM=CD=AD.
设CM=CD=AD=a,则AC=2a.
∵CF=AB,∴CF=FM=AB=BD.∴DM=BF.
∵∠BAD=∠ADB=∠CDM=∠M、∴△ABD∽△DCM.
3.解:(1)如图1,在AD 上取一点K,使BK=BC.
∵BD⊥AC,BK=BC,
∴∠BDC=90°,∠1=∠KBD,CD=KD.
∴∠C=90°-∠1,∠CBK=2∠1.
∵AB=AC,∴∠ABC=∠C=90°-∠1.
∴∠A=180°-∠ABC-∠C=2∠1=∠CBK.
又∠C=∠C,∴△CBK∽△CAB.
负值已舍).
(2)如图2,延长CB到点G,使BD=BG,连接AG,过点 A作AF⊥DE于点F.
∵∠ABC=90°,∴AB⊥BD.
又BD=BG,∴AG=AD.
∴∠DAG=2∠DAB,∠G=∠ADG.
又∠C=2∠DAB,∴∠DAG=∠C.
又∠G=∠G,∴△AGD∽△CGA.
∴∠ADG=∠CAG.∴∠G=∠CAG.∴AC=GC.
设BD=x,则 BG=x.
∵CD=6,∴AC=GC=6+2x,BC=6+x.
在 Rt△ABC中,根据勾股定理,
解得x=2(负值已舍).
∴AC=6+2x=10,BD=DG=2.
设∠C=2∠DAB=2α,则∠DAB=α.
∵∠ABC=90°,∴∠ADB=90°-α.
∵DE=CE,∴∠EDC=∠C=2α.
∴∠ADE=180°-∠ADB-∠EDC=90°-α=∠ADB.
∵AF⊥DE,∴∠AFD=90°=∠ABD.
又AD=AD,∠ADB=∠ADF,∴△ADB≌△ADF.
∴AB=AF=6,BD=FD=2.
设EF=y,则DE=CE=2+y.
∴AE=AC-CE=10-(2+y)=8-y.
在Rt△AFE 中,根据勾股定理,
解得
(3)如图3,延长CA 至点G,使BE=BG,过点 B 作BF⊥EG于点F.
∴EF=GF.
设∠ACB=2α,则
∵BE=BG,∴∠BEA=∠G=90°-α.
∴∠EBG=180°-∠BEA-∠G=2α=∠ACB.
又∠G=∠G,∴△EBG∽△BCG.
∴∠BEG=∠CBG.∴∠G=∠CBG.∴CB=CG.
∵CD⊥AB,BF⊥EG,∴∠D=∠BFA=90°.
又∠CAD=∠BAF,AC=AB,
∴△CAD≌△BAF.∴AD=AF=7.
∵AE=1,∴GF=EF=AF+AE=7+1=8.
设AC=x,则AB=x,BC=CG=AC+AF+GF=x+7+8=x+15,BD=AB+AD=x+7.
在Rt△ACD和Rt△BCD 中,根据勾股定理,
即 7) .解得x=25(负值已舍).
∴BC=25+15=40.
4.解:(1)选择方法一.
如图1,延长ED 至点H,使DH=DF,连接CH.
∵∠FDB =∠EDA =45°,∴∠BDH =∠EDA =45°,∠EDF=180°-∠EDF=180°-∠EDA=90°.
又CD=CD、DF=DH,∴△FDC≌△HDC.
∴CH=CF,∠F=∠H.
∵EC=CF,∴EC=CH.∴∠E=∠H.∴∠E=∠F.
∵∠EOC=∠FOD,∴∠ECF=∠EDF=90°.
一题多解选择方法二.
如图2,延长FD 至点H,使DH=DE,连接CH.
∵∠FDB=∠EDA =45°,∴∠CDH=∠FDB=45°=∠EDA,∠EDF=180°-∠EDA-∠FDB=90°.
又CD=CD,DE=DH,∴△EDC≌△HDC.
∴EC=HC,∠E=∠H.
∵EC=CF,∴CF=HC.∴∠F=∠H=∠E.
∵∠EOC=∠FOD,∴∠ECF=∠EDF=90°.
(2)AF=EF+DE.理由如下:
如图3,延长FE 至点H,使HE=DE,连接AH,AD.
∵∠AED=∠CEF,∠CEF=∠AEH,
∴∠AED=∠AEH.
又DE=HE,AE=AE,∴△AED≌△AEH.
∴∠HAE=∠DAE.
∵在 Rt△ABC 中,∠BAC=90°,D 是BC 的中点.
∴AD=CD.∴∠C=∠DAE=∠HAE.∴AH∥CB.
∴∠H=∠CFE=∠AFB=∠HAF.∴AF=HF.
∵HF=EF+EH,∴AF=EF+DE.
(3)如图4,延长 DA 至点F,使AF=AC,过点 F 作FG⊥DB 于点G,连接BF.
∠BAC.
又AF=AC,AB=AB,∴△ABF≌△ABC.∴BF=BC.
又AD∥BC,∴∠BAF=∠ABC=∠ABF.
∴BF=AF=AC=BC.∴四边形ACBF 是菱形.
∴BF∥AC.∴∠FBG=∠BEC=60°.
∵FG⊥BD,∴∠FGB=∠FGD=90°.∴∠BFG=30°.
设AC=BC=BF=AF=x,则
在 Rt△BFG 中,根据勾股定理,得
∵AD=5,BD=15,∴DF=5+x,DG=15- x.
在 Rt△FDG 中,根据勾股定理,
5.解:(1)如图1,在 BD 上取一点E,使BE=CE,过点 C 作CF⊥BD 于点 F.
∴∠CBD=∠ECB,∠EFC=90°.
∴∠DEC=2∠CBD=2∠ECB.
∵∠ABD=2∠CBD,∴∠DEC=∠ABD.
∵四边形ABCD 是平行四边形,
∴∠EDC=∠ABD.∴∠DEC=∠EDC.
∴CD=CE=BE=5.∴EF=DF.
∵在 Rt△BFC 和 Rt△EFC 中,根据勾股定理,
即
∴DF=EF=4.∴BD=BE+EF+DF=5+4+4=13.
一题多解如图2,在 DB 的延长线上取一点E,使BE=AB,过点A 作AF⊥BD于点F.
∴∠E=∠EAB,∠AFB=90°.
∴∠ABD=2∠E=2∠EAB.
∵∠ABD=2∠CBD,∴∠E=∠CBD.
∵四边形 ABCD 是平行四边形,
∴CD=AB=BE=5,AD∥BC.∴∠ADB=∠CBD.
∴∠ADB=∠E.∴AD=AE=3
∵AF⊥BD,∴EF=DF.
∵在 Rt△BFA 和 Rt△EFA 中,根据勾股定理, 即
∴BF=4.∴DF=EF=5+4=9.
∴BD=BF+DF=4+9=13.
(2)如图3,过点D作DM∥BC,交AB 于点M,DN∥AB交BC 于点 N,DH⊥BC 于点 H.
∴四边形 BNDM 是平行四边形、∠AMD =∠ABC、∠ABC=∠DNC.
∵∠A=∠C=∠ABC,∴∠A=∠AMD、∠C=∠DNC、
∵DH⊥BC,∴NH=CH.
由(1),得BD=13.
∵在 Rt△BDH 和 Rt△NDH 中.根据勾股定理,
即
(3)BC 的长为
详解如图4,延长CB 至点 Q,使 BQ=DC,过点 A 作AP⊥BC 于点 P,连接AQ,AC.
∴∠APQ=90°.
∵∠BAD+∠BCD=180°,∠BAD+∠BCD+∠ADC+∠ABC=360°,∴∠ADC+∠ABC=180°.
又∠ABQ+∠ABC=180°,∴∠ADC=∠ABQ.
又AD=AB,DC=BQ,∴△ADC≌△ABQ.
∴AC=AQ,∠CAD=∠QAB.∴∠QAC=∠BAD.
∵AP⊥BC,∴PQ=PC,∠QAP=∠CAP.
设∠CBD=a.
∵AB=AD,∠ABD=2∠CBD,∴∠ADB=∠ABD=2a.
∴∠CAD=∠QAB=∠QAP-∠BAP=a,∠ACD=∠Q=90°-∠QAP=2a.∴∠ACD=2∠CAD.
在AC上取一点G,使AG=DG,过点 D 作 DK⊥AC 于点 K.
同理(1)可得,AQ=AC=13.
∵在 Rt△APQ 和 Rt△APB 中,根据勾股定理,
即
同课章节目录
