2025年中考数学二轮复习专题3 利用顶点在同一直线上的三个相等角解决问题(含答案)
文档属性
| 名称 | 2025年中考数学二轮复习专题3 利用顶点在同一直线上的三个相等角解决问题(含答案) |  | |
| 格式 | docx | ||
| 文件大小 | 327.8KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 通用版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2025-05-29 13:42:34 | ||
图片预览



文档简介
专题3 利用顶点在同一直线上的三个相等角解决问题
1.难点分解练
核心归纳
编写说明:将此类难题的核心要点总结,结合例题加深理解,之后练综合题目易有解题思路.
类型 何时用 经典模型图 常用结论
等角 为直角 题中有直角或有2个直角的顶点在一条直线上 在△ABC 和△DEB 中,A,B,D 三点共线,共线的三个角为直角.
同侧型 异侧型 子母型
△ABC≌△DEB
△ABC∽△DEB
等 角为锐 角 或钝角 题中有 2个等角(锐角或钝角)的顶点在一条直线上(或一条直线上的一个角α的两边有数量关系,且直线上有另一 个 角 在△ADB 和△CEA 中,A,D,E三点共线,且∠1=∠2=∠3.
同侧型 异侧型 中点型(A 为ED 的中点)
△ADB≌△CEA
△ADB∽△CEA
类型突破
编写说明:每类例题由浅入深设置,包含该类型的经典情况且在不同几何图形背景下,让学生先练透每个类型,抓住核心本质后再综合练习.
类型1·等角为直角
例1.如图,在等腰 Rt△ABC中,∠ABC=90°,AB=BC,D 是△ABC 内一点,且AD=AB,连接BD,CD,若BD=2,求△BCD 的面积.
例2.如图,四边形ABCD 是正方形,E是 DC 上方一点, ,F 是 EC的延长线上一点,连接BF,已知 求CF 的长.
类型2·等角为锐角或钝角
例3.如图, ,E 是CB 的延长线上一点,连接DE 交AB 于点 F,连接AE,AD,若 与 互补,探究CD 与EF 的数量关系.
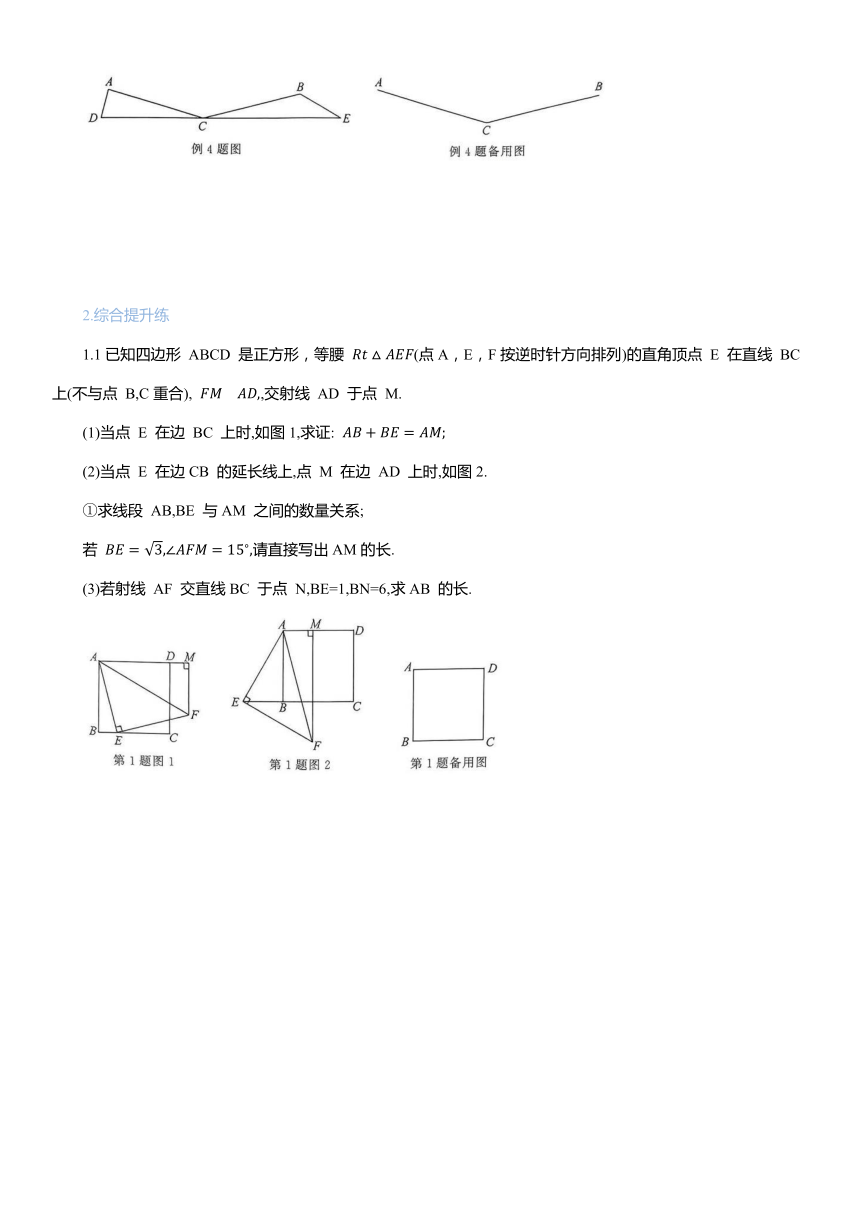
例4.学难如图, ,D,C,E 三点共线, 求 的面积.
2.综合提升练
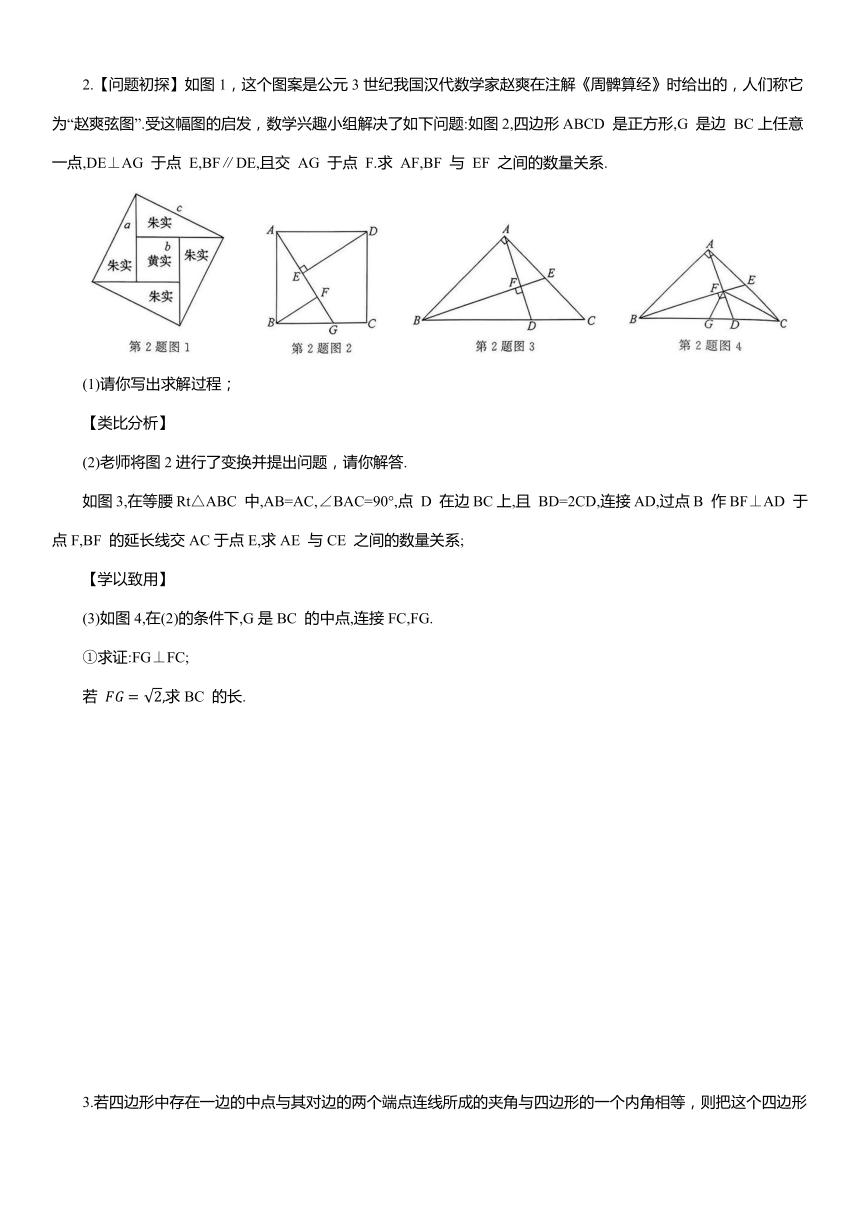
1.1已知四边形 ABCD 是正方形,等腰 (点A,E,F按逆时针方向排列)的直角顶点 E 在直线 BC 上(不与点 B,C重合), ,交射线 AD 于点 M.
(1)当点 E 在边 BC 上时,如图1,求证:
(2)当点 E 在边CB 的延长线上,点 M 在边 AD 上时,如图2.
①求线段 AB,BE 与AM 之间的数量关系;
若 请直接写出AM的长.
(3)若射线 AF 交直线BC 于点 N,BE=1,BN=6,求AB 的长.
2.【问题初探】如图1,这个图案是公元3世纪我国汉代数学家赵爽在注解《周髀算经》时给出的,人们称它为“赵爽弦图”.受这幅图的启发,数学兴趣小组解决了如下问题:如图2,四边形ABCD 是正方形,G 是边 BC上任意一点,DE⊥AG 于点 E,BF∥DE,且交 AG 于点 F.求 AF,BF 与 EF 之间的数量关系.
(1)请你写出求解过程;
【类比分析】
(2)老师将图2进行了变换并提出问题,请你解答.
如图3,在等腰Rt△ABC 中,AB=AC,∠BAC=90°,点 D 在边BC上,且 BD=2CD,连接AD,过点B 作BF⊥AD 于点F,BF 的延长线交AC于点E,求AE 与CE 之间的数量关系;
【学以致用】
(3)如图4,在(2)的条件下,G是BC 的中点,连接FC,FG.
①求证:FG⊥FC;
若 求BC 的长.
3.若四边形中存在一边的中点与其对边的两个端点连线所成的夹角与四边形的一个内角相等,则把这个四边形叫做“中角等四边形”.
(1)若矩形 ABCD 是“中角等四边形”,则矩形 ABCD 两条相邻边的比 是 ;
(2)如图,若菱形 ABCD 是“中角等四边形”,求 tan A 的值;
(3)若 ABCD 是“中角等四边形”, 求 CD 两邻边之比
4.【模型建立】
(1)如图1,在△AFC 中,∠F=α,将线段AC 绕点A 逆时针旋转角β得到线段AB,E 为线段AF上一点,已知∠BEA=∠F=α,α+β=180°.求证:△ABE≌△CAF;
【类比应用】
(2)如图2,在△ABC中,AB=AC,D 是△ABC外一点,∠D=∠BAC,过点B 作BE∥CD,交DA 的延长线于点E、在图中找出与AD 相等的线段,并证明;
【拓展探究】
(3)如图3,直线 交x轴于点A,交y轴于点C,点 B 与点A 关于y 轴对称,动点E,F分别在线段AB,AC上(点E 不与点A,B 重合),且∠CEF=∠CAO.
①当CF=EF 时,求点 F 的坐标;
是否存在点E,使△CEF 的面积被y轴平分 若存在,求△CEF 的面积;若不存在,请说明理由.
专题3 利用顶点在同一直线上的三个相等角解决问题
例1.解:如图,过点C作CN⊥BD交BD 的延长线于点N,过点A 作AM⊥BD 于点M、
∴∠AMB=∠N=90°.∴∠BAM+∠ABM=90°.
∵∠ABC=90°、∴∠CBN+∠ABM=90°.
∴∠BAM=∠CBN.
又∠AMB=∠N,AB=BC,
∴△ABM≌△BCN.
∴BM=CN.
∵AD=AB,AM⊥BD,BD=2,∴BM= BD=1.
例2.解:如图,过点 D 作DG⊥EC 于点G,过点 B 作BH⊥CF 于点H.
∴∠DGE=∠DGC=∠BHF=∠CHB=90°.
∴∠DCG+∠GDC=90°.
∵四边形ABCD为正方形,
∴DC=CB,∠DCB=90°.
∴∠DCG+∠HCB=90°.∴∠GDC=∠HCB.
又∠DGC=∠CHB,DC=CB,
∴△DGC≌△CHB.
∴DG=CH.
在Rt△DEG中,∵∠E=45°,DE=3
在Rt△BHF 中,
∴设BH=3x,FH=4x.
根据勾股定理,得
∴5x=10.∴x=2.∴FH=8.
∴CF=CH+FH=3+8=11.
例3.解:如图,在ED上取一点Q,使CQ=CD.
∴∠CQD=∠CDQ.
∵∠AFE 与∠AEC 互补,∠AFE 与∠AFD 互补,
∴∠AEC=∠AFD.
∴∠AEF+∠CEQ=∠AEF+∠EAF,即∠EAF=∠CEQ.
∵AB∥CD,∴∠AFD=∠CDQ=∠CQD.
∴∠AFE=∠EQC.
又∠EAF=∠CEQ,∴△AFE∽△EQC.
∵AE=2EC,∴EF=2CQ=2CD.
例4.解:当点 A,B 在 DE 的同侧时,如图1,在CE 上取一点T,使BT=BE,在DC 上取一点R,使∠DAR=∠ADC=75°,过点 A 作 AW⊥CD 于点 W,过点 B 作 BL⊥CE 于点L.
∴AR=DR,∠ARC=∠ADC+∠DAR=150°,∠BTE=
ET=2EL=2BE×cosE=2 ×cos30°=3.
∴∠ACR+∠BCT=30°,∠CBT+∠BCT=30°,CT=CE-ET=5-3=2.∴∠ACR=∠CBT.
又AC=CB,∠ARC=∠CTB,∴△ACR≌△CBT.
∴AR=DR=2.∴CD=DR+CR=2+
∵∠ARC=150°,∴∠ARW=30°.
又
当点A,B 在DE 的异侧时,如图2,在CE 上取一点 P,使 连接AP,过点 A 作AK⊥DP 于点 K.
∴∠DKA=∠AKP=90°.
∵∠E=30°,∴∠B+∠ECB=150°.
又∠ACP+∠ECB=∠ACB=150°,∴∠ACP=∠B.
又AC=CB,CP=BE,∴△ACP≌△CBE.
∴AP=CE=5,∠APC=∠E=30°.
∴在Rt△AKP 中,
∵∠ADC=75°,∴∠PAD=75°=∠ADC.
∴AP=PD=5.∴CD=PD-CP=5-
综上所述,△AOC 的面积为 或
1.解:(1)证明:如图1,延长MF 交边BC 的延长线于点 H.
∵四边形ABCD 是正方形、FM⊥AD,
∴∠ABE=∠BAD=∠M=90°,AM∥BH.
∴四边形ABHM 为矩形.
∴∠H=90°,AM=BH=BE+EH.
∴∠EFH+∠FEH=90°.
∵△AEF 为等腰直角三角形,
∴AE=EF,∠AEF=90°.∴∠AEB+∠FEH=90°.
∴∠AEB=∠EFH.
又∠B=∠H,AE=EF,∴△ABE≌△EHF.∴AB=EH.
∴AM=BE+AB,即AB+BE=AM.
(2)①如图2,设 BC 与MF 相交于点 H.
由(1),得 AE=EF,∠AEF=90°,∠DAB=∠ABH =∠AMH=90°.∴∠AEB+∠FEH=∠AEB+∠EAB=90°,四边形ABHM 为矩形.
∴∠EAB=∠FEH,AM=BH,∠BHM=90°.
∴∠ABE=∠EHF=90°.
又AE=EF,∠EAB=∠FEH,∴△ABE≌△EHF.
∴AB=EH=BE+BH.
∴AB=BE+AM.
②AM 的长为
详解由①,得四边形ABHM 是矩形.
∴AB∥MH.∴∠BAF=∠AFM=15°.
∵△AEF 为等腰直角三角形,∴∠FAE=45°.
∴∠BAE=∠FAE-∠BAF=30°.
∴在 Rt△ABE 中,
由①,得AB=BE+AM.
∴AM=AB-BE=3-
(3)当射线AF 与BC 的延长线相交于点N 时,如图3,延长MF 交BN 于点K.
由(1),得△ABE≌△EKF,四边形ABKM 是矩形.
∴AB=EK,BE=KF=1,AB∥MK.
∵BN=6,∴KN=BN-BE-EK=6-1-AB=5-AB.
∴AB=2或3.
当射线AF 与边BC 相交于点N 时,如图4,设 MF 交BC于点K.
由(2)①,得△ABE≌△EKF,∠ABN=∠FKN=90°.
∴BE=KF=1,AB=EK,AB∥KF.
∴△ABN∽△FKN.
∵BN=6,∴KN=EK-BE-BN=AB-7.
(负值已舍).
综上所述,AB 的长为2或3或
2.解:(1)∵四边形 ABCD 是正方形,
∴∠BAD=90°,BA=AD.∴∠BAF+∠EAD=90°.
∵DE⊥AG,BF∥DE,∴∠BFA=∠DEF=∠AED=90°.
∴∠BAF+∠FBA=90°.∴∠FBA=∠EAD.
又∠BFA=∠AED,BA=AD,∴△FBA≌△EAD.
∴BF=AE.
∵EF=AF-AE,∴EF=AF-BF.
(2)如图1,过点C作CH⊥AD交AD的延长线于点 H.
∴∠H=90°.∴∠HAC+∠ACH=90°.
∵BF⊥AD,∴∠BFA=∠BFD=90°.
∵∠BAC=∠BAF+∠HAC=90°,∴∠BAF=∠ACH.又∠BFA=∠H=90°,BA=AC,∴△BFA≌△AHC.
∴AF=CH,BF=AH.
∵∠H=∠BFD=90°,∠BDF=∠CDH、
∴△BFD∽△CHD,BF∥CH.∴BE=BD.
∵BD=2CD、∴BF=2CH.∴AH=2AF、
(3)如图2,过点C作CH⊥AD交AD 的延长线于点 H,过点G作GM⊥GF 交BF 于点M,连接AG 交BF 于点 N.
∵AB=AC,∠BAC=90°,G是BC 的中点,
∴AG=BG,AG⊥BC.∴∠AGB=∠FGM=90°.
∴∠FGA=∠MGB.
∵BF⊥AD,∴∠BFA=90°=∠AGB.
又∠ANF=∠BNG,∴∠GAF=∠GBM.
又AG=BG,∠FGA=∠MGB,∴△FGA≌△MGB.
∴FG=MG.∴∠GMF=∠GFM=45°.∴∠GFD与45°.
由(2),知CH=AF=FH.
又∠H=90°,∴∠HFC=45°.
∴∠GFC=∠HFC+∠GFD=90°.∴FG⊥FC.
②如图2,由(3)①,知∠GFM=∠HFC=45°,△FGA≌△MGB.∴AF=BM.
在 Rt△MGF 中 在 Rt△FHC中,
由(2),知/
又
∴AF=FH=2.∴FC=2
在Rt△GFC 中,根据勾股定理,得
∵G为BC的中点,.
3.解:(1) 详解根据题意,得矩形ABCD 长边的中点与其对边的两个端点连线所成的夹角与矩形的一个内角相等.如图1,设BC的中点为G,∴BG=CG.
∵矩形 ABCD 是“中角等四边形”,
∴∠B=∠C=90°,AB=CD,∠AGD=90°.
又BG=CG,∴△ABG≌△DCG.∴∠AGB=∠DGC.
∵∠AGB+∠AGD+∠DGC=180°,
∴∠AGB=45°.∴∠BAG=45°=∠AGB.
即
(2)如图2,设 AB 的中点为G,在AB 的延长线上取一点H,使CB=CH,过点C作CE⊥BH 于点E.
∵菱形 ABCD 是“中角等四边形”,
∴AD=AB=BC,∠A=∠DGC,AD∥BC.
∵∠DGB=∠DGC+∠CGH=∠A+∠GDA,
∴∠GDA=∠CGH.
又∠A=∠H,∴△GDA∽△CGH.
设AG=BG=a.∴AB=AD=BC=2a.
:JIG=4a.∴BH=3a.∴BE= a.
在 Rt△CBE中,根据勾股定理,得
(3)当 ABCD 的较长边AB的中点G与对边CD 的两个端点连线所成的夹角为锐角时,如图3,在AB 的延长线上取一点H,使CB=CH,过点C作CE⊥BH于点E.
∵□ABCD 是“中角等四边形”,
∴AD=BC=CH,∠A=∠DGC,AD∥BC.
∴∠A=∠CBH=∠H.
∵∠DGB=∠DGC+∠CGH=∠A+∠GDA,
∴∠GDA=∠CGH.
又∠A=∠H,∴△GDA∽△CGH.∴D/C=△GAC.
∴设 BE=3a,CE=4a.
根据勾股定理、得
设
负值已舍).
当 ABCD的较长边AB的中点G与对边CD 的两个端点连线所成的夹角为钝角时,如图4,在AB 上取一点 P,使DA=DP,过点 D作DQ⊥AB 于点Q.
∴∠A=∠DPA,AQ=PQ,AG=BG= AB.
同理上种情况,得△GCB∽△DGP. 学习之
同理上种情况.得 设 PD=m.
(负值已舍).
当 ABCD的较短边AD的中点G 与对边BC的两个端点连线所成的夹角为锐角时,同理可得, (负值已舍).
此种情况不存在.
综上所述,□ABCD 的两条邻边之比为 或
4.解:(1)证明:根据旋转的性质,得∠BAC=β,AB=CA.
∵∠BEA=α,α+β=180°,∴∠BEA+∠BAC=180°.
∵∠BEA+∠BEF=180°,∴∠BEF=∠BAC.
∴∠B+∠BAE=∠BAE+∠CAF.∴∠B=∠CAF.又∠BEA=∠F,AB=CA,∴△ABE≌△CAF.
(2)BE=AD、
证明:如图1,在AE上取一点 F,使BE=BF.
∴∠E=∠BFE.
∵BE∥CD,∴∠E+∠D=180°.∴∠BFE+∠D=180°.
∵∠BFE+∠BFA=180°,∴∠BFA=∠D.
∵∠D=∠BAC,∠FAB+∠BAC=∠DCA+∠D,
∴∠FAB=∠DCA.
又AB=CA,∠BFA=∠D,∴△FAB≌△DCA.
∴BF=AD.∴BE=AD.
③④在 中,令y=0,则x=-8;令x=0,则y=6.
∴A(-8,0),C(0,6).∴OA=8,OC=6.
根据勾股定理,得
∵CF=EF,∴∠ECF=∠CEF=∠CAO.∴AE=CE.
如图2,过点 E 作EG⊥AC 于点G,过点 F 作FK⊥CE于点K,FH⊥AB于点H.
②存在、
如图3,设EF 交y轴于点M,过点 F 作FN⊥OA 于点N.
∵点B 与点 A 关于y轴对称,∴OA=OB=8,AC=BC=10.
∴∠FAE=∠EBC.
∵∠CEF=∠CAO,∴∠AFE+∠FEA=∠FEA+∠BEC.
∴∠AFE=∠BEC.
又∠FAE=∠EBC,∴△AFE∽△BEC.∴AE=AEC.
∵△CEF的面积被y轴平分,
∴OA-ON=OB-OE,即AN=BE.
由①,知
由①,知
即
1.难点分解练
核心归纳
编写说明:将此类难题的核心要点总结,结合例题加深理解,之后练综合题目易有解题思路.
类型 何时用 经典模型图 常用结论
等角 为直角 题中有直角或有2个直角的顶点在一条直线上 在△ABC 和△DEB 中,A,B,D 三点共线,共线的三个角为直角.
同侧型 异侧型 子母型
△ABC≌△DEB
△ABC∽△DEB
等 角为锐 角 或钝角 题中有 2个等角(锐角或钝角)的顶点在一条直线上(或一条直线上的一个角α的两边有数量关系,且直线上有另一 个 角 在△ADB 和△CEA 中,A,D,E三点共线,且∠1=∠2=∠3.
同侧型 异侧型 中点型(A 为ED 的中点)
△ADB≌△CEA
△ADB∽△CEA
类型突破
编写说明:每类例题由浅入深设置,包含该类型的经典情况且在不同几何图形背景下,让学生先练透每个类型,抓住核心本质后再综合练习.
类型1·等角为直角
例1.如图,在等腰 Rt△ABC中,∠ABC=90°,AB=BC,D 是△ABC 内一点,且AD=AB,连接BD,CD,若BD=2,求△BCD 的面积.
例2.如图,四边形ABCD 是正方形,E是 DC 上方一点, ,F 是 EC的延长线上一点,连接BF,已知 求CF 的长.
类型2·等角为锐角或钝角
例3.如图, ,E 是CB 的延长线上一点,连接DE 交AB 于点 F,连接AE,AD,若 与 互补,探究CD 与EF 的数量关系.
例4.学难如图, ,D,C,E 三点共线, 求 的面积.
2.综合提升练
1.1已知四边形 ABCD 是正方形,等腰 (点A,E,F按逆时针方向排列)的直角顶点 E 在直线 BC 上(不与点 B,C重合), ,交射线 AD 于点 M.
(1)当点 E 在边 BC 上时,如图1,求证:
(2)当点 E 在边CB 的延长线上,点 M 在边 AD 上时,如图2.
①求线段 AB,BE 与AM 之间的数量关系;
若 请直接写出AM的长.
(3)若射线 AF 交直线BC 于点 N,BE=1,BN=6,求AB 的长.
2.【问题初探】如图1,这个图案是公元3世纪我国汉代数学家赵爽在注解《周髀算经》时给出的,人们称它为“赵爽弦图”.受这幅图的启发,数学兴趣小组解决了如下问题:如图2,四边形ABCD 是正方形,G 是边 BC上任意一点,DE⊥AG 于点 E,BF∥DE,且交 AG 于点 F.求 AF,BF 与 EF 之间的数量关系.
(1)请你写出求解过程;
【类比分析】
(2)老师将图2进行了变换并提出问题,请你解答.
如图3,在等腰Rt△ABC 中,AB=AC,∠BAC=90°,点 D 在边BC上,且 BD=2CD,连接AD,过点B 作BF⊥AD 于点F,BF 的延长线交AC于点E,求AE 与CE 之间的数量关系;
【学以致用】
(3)如图4,在(2)的条件下,G是BC 的中点,连接FC,FG.
①求证:FG⊥FC;
若 求BC 的长.
3.若四边形中存在一边的中点与其对边的两个端点连线所成的夹角与四边形的一个内角相等,则把这个四边形叫做“中角等四边形”.
(1)若矩形 ABCD 是“中角等四边形”,则矩形 ABCD 两条相邻边的比 是 ;
(2)如图,若菱形 ABCD 是“中角等四边形”,求 tan A 的值;
(3)若 ABCD 是“中角等四边形”, 求 CD 两邻边之比
4.【模型建立】
(1)如图1,在△AFC 中,∠F=α,将线段AC 绕点A 逆时针旋转角β得到线段AB,E 为线段AF上一点,已知∠BEA=∠F=α,α+β=180°.求证:△ABE≌△CAF;
【类比应用】
(2)如图2,在△ABC中,AB=AC,D 是△ABC外一点,∠D=∠BAC,过点B 作BE∥CD,交DA 的延长线于点E、在图中找出与AD 相等的线段,并证明;
【拓展探究】
(3)如图3,直线 交x轴于点A,交y轴于点C,点 B 与点A 关于y 轴对称,动点E,F分别在线段AB,AC上(点E 不与点A,B 重合),且∠CEF=∠CAO.
①当CF=EF 时,求点 F 的坐标;
是否存在点E,使△CEF 的面积被y轴平分 若存在,求△CEF 的面积;若不存在,请说明理由.
专题3 利用顶点在同一直线上的三个相等角解决问题
例1.解:如图,过点C作CN⊥BD交BD 的延长线于点N,过点A 作AM⊥BD 于点M、
∴∠AMB=∠N=90°.∴∠BAM+∠ABM=90°.
∵∠ABC=90°、∴∠CBN+∠ABM=90°.
∴∠BAM=∠CBN.
又∠AMB=∠N,AB=BC,
∴△ABM≌△BCN.
∴BM=CN.
∵AD=AB,AM⊥BD,BD=2,∴BM= BD=1.
例2.解:如图,过点 D 作DG⊥EC 于点G,过点 B 作BH⊥CF 于点H.
∴∠DGE=∠DGC=∠BHF=∠CHB=90°.
∴∠DCG+∠GDC=90°.
∵四边形ABCD为正方形,
∴DC=CB,∠DCB=90°.
∴∠DCG+∠HCB=90°.∴∠GDC=∠HCB.
又∠DGC=∠CHB,DC=CB,
∴△DGC≌△CHB.
∴DG=CH.
在Rt△DEG中,∵∠E=45°,DE=3
在Rt△BHF 中,
∴设BH=3x,FH=4x.
根据勾股定理,得
∴5x=10.∴x=2.∴FH=8.
∴CF=CH+FH=3+8=11.
例3.解:如图,在ED上取一点Q,使CQ=CD.
∴∠CQD=∠CDQ.
∵∠AFE 与∠AEC 互补,∠AFE 与∠AFD 互补,
∴∠AEC=∠AFD.
∴∠AEF+∠CEQ=∠AEF+∠EAF,即∠EAF=∠CEQ.
∵AB∥CD,∴∠AFD=∠CDQ=∠CQD.
∴∠AFE=∠EQC.
又∠EAF=∠CEQ,∴△AFE∽△EQC.
∵AE=2EC,∴EF=2CQ=2CD.
例4.解:当点 A,B 在 DE 的同侧时,如图1,在CE 上取一点T,使BT=BE,在DC 上取一点R,使∠DAR=∠ADC=75°,过点 A 作 AW⊥CD 于点 W,过点 B 作 BL⊥CE 于点L.
∴AR=DR,∠ARC=∠ADC+∠DAR=150°,∠BTE=
ET=2EL=2BE×cosE=2 ×cos30°=3.
∴∠ACR+∠BCT=30°,∠CBT+∠BCT=30°,CT=CE-ET=5-3=2.∴∠ACR=∠CBT.
又AC=CB,∠ARC=∠CTB,∴△ACR≌△CBT.
∴AR=DR=2.∴CD=DR+CR=2+
∵∠ARC=150°,∴∠ARW=30°.
又
当点A,B 在DE 的异侧时,如图2,在CE 上取一点 P,使 连接AP,过点 A 作AK⊥DP 于点 K.
∴∠DKA=∠AKP=90°.
∵∠E=30°,∴∠B+∠ECB=150°.
又∠ACP+∠ECB=∠ACB=150°,∴∠ACP=∠B.
又AC=CB,CP=BE,∴△ACP≌△CBE.
∴AP=CE=5,∠APC=∠E=30°.
∴在Rt△AKP 中,
∵∠ADC=75°,∴∠PAD=75°=∠ADC.
∴AP=PD=5.∴CD=PD-CP=5-
综上所述,△AOC 的面积为 或
1.解:(1)证明:如图1,延长MF 交边BC 的延长线于点 H.
∵四边形ABCD 是正方形、FM⊥AD,
∴∠ABE=∠BAD=∠M=90°,AM∥BH.
∴四边形ABHM 为矩形.
∴∠H=90°,AM=BH=BE+EH.
∴∠EFH+∠FEH=90°.
∵△AEF 为等腰直角三角形,
∴AE=EF,∠AEF=90°.∴∠AEB+∠FEH=90°.
∴∠AEB=∠EFH.
又∠B=∠H,AE=EF,∴△ABE≌△EHF.∴AB=EH.
∴AM=BE+AB,即AB+BE=AM.
(2)①如图2,设 BC 与MF 相交于点 H.
由(1),得 AE=EF,∠AEF=90°,∠DAB=∠ABH =∠AMH=90°.∴∠AEB+∠FEH=∠AEB+∠EAB=90°,四边形ABHM 为矩形.
∴∠EAB=∠FEH,AM=BH,∠BHM=90°.
∴∠ABE=∠EHF=90°.
又AE=EF,∠EAB=∠FEH,∴△ABE≌△EHF.
∴AB=EH=BE+BH.
∴AB=BE+AM.
②AM 的长为
详解由①,得四边形ABHM 是矩形.
∴AB∥MH.∴∠BAF=∠AFM=15°.
∵△AEF 为等腰直角三角形,∴∠FAE=45°.
∴∠BAE=∠FAE-∠BAF=30°.
∴在 Rt△ABE 中,
由①,得AB=BE+AM.
∴AM=AB-BE=3-
(3)当射线AF 与BC 的延长线相交于点N 时,如图3,延长MF 交BN 于点K.
由(1),得△ABE≌△EKF,四边形ABKM 是矩形.
∴AB=EK,BE=KF=1,AB∥MK.
∵BN=6,∴KN=BN-BE-EK=6-1-AB=5-AB.
∴AB=2或3.
当射线AF 与边BC 相交于点N 时,如图4,设 MF 交BC于点K.
由(2)①,得△ABE≌△EKF,∠ABN=∠FKN=90°.
∴BE=KF=1,AB=EK,AB∥KF.
∴△ABN∽△FKN.
∵BN=6,∴KN=EK-BE-BN=AB-7.
(负值已舍).
综上所述,AB 的长为2或3或
2.解:(1)∵四边形 ABCD 是正方形,
∴∠BAD=90°,BA=AD.∴∠BAF+∠EAD=90°.
∵DE⊥AG,BF∥DE,∴∠BFA=∠DEF=∠AED=90°.
∴∠BAF+∠FBA=90°.∴∠FBA=∠EAD.
又∠BFA=∠AED,BA=AD,∴△FBA≌△EAD.
∴BF=AE.
∵EF=AF-AE,∴EF=AF-BF.
(2)如图1,过点C作CH⊥AD交AD的延长线于点 H.
∴∠H=90°.∴∠HAC+∠ACH=90°.
∵BF⊥AD,∴∠BFA=∠BFD=90°.
∵∠BAC=∠BAF+∠HAC=90°,∴∠BAF=∠ACH.又∠BFA=∠H=90°,BA=AC,∴△BFA≌△AHC.
∴AF=CH,BF=AH.
∵∠H=∠BFD=90°,∠BDF=∠CDH、
∴△BFD∽△CHD,BF∥CH.∴BE=BD.
∵BD=2CD、∴BF=2CH.∴AH=2AF、
(3)如图2,过点C作CH⊥AD交AD 的延长线于点 H,过点G作GM⊥GF 交BF 于点M,连接AG 交BF 于点 N.
∵AB=AC,∠BAC=90°,G是BC 的中点,
∴AG=BG,AG⊥BC.∴∠AGB=∠FGM=90°.
∴∠FGA=∠MGB.
∵BF⊥AD,∴∠BFA=90°=∠AGB.
又∠ANF=∠BNG,∴∠GAF=∠GBM.
又AG=BG,∠FGA=∠MGB,∴△FGA≌△MGB.
∴FG=MG.∴∠GMF=∠GFM=45°.∴∠GFD与45°.
由(2),知CH=AF=FH.
又∠H=90°,∴∠HFC=45°.
∴∠GFC=∠HFC+∠GFD=90°.∴FG⊥FC.
②如图2,由(3)①,知∠GFM=∠HFC=45°,△FGA≌△MGB.∴AF=BM.
在 Rt△MGF 中 在 Rt△FHC中,
由(2),知/
又
∴AF=FH=2.∴FC=2
在Rt△GFC 中,根据勾股定理,得
∵G为BC的中点,.
3.解:(1) 详解根据题意,得矩形ABCD 长边的中点与其对边的两个端点连线所成的夹角与矩形的一个内角相等.如图1,设BC的中点为G,∴BG=CG.
∵矩形 ABCD 是“中角等四边形”,
∴∠B=∠C=90°,AB=CD,∠AGD=90°.
又BG=CG,∴△ABG≌△DCG.∴∠AGB=∠DGC.
∵∠AGB+∠AGD+∠DGC=180°,
∴∠AGB=45°.∴∠BAG=45°=∠AGB.
即
(2)如图2,设 AB 的中点为G,在AB 的延长线上取一点H,使CB=CH,过点C作CE⊥BH 于点E.
∵菱形 ABCD 是“中角等四边形”,
∴AD=AB=BC,∠A=∠DGC,AD∥BC.
∵∠DGB=∠DGC+∠CGH=∠A+∠GDA,
∴∠GDA=∠CGH.
又∠A=∠H,∴△GDA∽△CGH.
设AG=BG=a.∴AB=AD=BC=2a.
:JIG=4a.∴BH=3a.∴BE= a.
在 Rt△CBE中,根据勾股定理,得
(3)当 ABCD 的较长边AB的中点G与对边CD 的两个端点连线所成的夹角为锐角时,如图3,在AB 的延长线上取一点H,使CB=CH,过点C作CE⊥BH于点E.
∵□ABCD 是“中角等四边形”,
∴AD=BC=CH,∠A=∠DGC,AD∥BC.
∴∠A=∠CBH=∠H.
∵∠DGB=∠DGC+∠CGH=∠A+∠GDA,
∴∠GDA=∠CGH.
又∠A=∠H,∴△GDA∽△CGH.∴D/C=△GAC.
∴设 BE=3a,CE=4a.
根据勾股定理、得
设
负值已舍).
当 ABCD的较长边AB的中点G与对边CD 的两个端点连线所成的夹角为钝角时,如图4,在AB 上取一点 P,使DA=DP,过点 D作DQ⊥AB 于点Q.
∴∠A=∠DPA,AQ=PQ,AG=BG= AB.
同理上种情况,得△GCB∽△DGP. 学习之
同理上种情况.得 设 PD=m.
(负值已舍).
当 ABCD的较短边AD的中点G 与对边BC的两个端点连线所成的夹角为锐角时,同理可得, (负值已舍).
此种情况不存在.
综上所述,□ABCD 的两条邻边之比为 或
4.解:(1)证明:根据旋转的性质,得∠BAC=β,AB=CA.
∵∠BEA=α,α+β=180°,∴∠BEA+∠BAC=180°.
∵∠BEA+∠BEF=180°,∴∠BEF=∠BAC.
∴∠B+∠BAE=∠BAE+∠CAF.∴∠B=∠CAF.又∠BEA=∠F,AB=CA,∴△ABE≌△CAF.
(2)BE=AD、
证明:如图1,在AE上取一点 F,使BE=BF.
∴∠E=∠BFE.
∵BE∥CD,∴∠E+∠D=180°.∴∠BFE+∠D=180°.
∵∠BFE+∠BFA=180°,∴∠BFA=∠D.
∵∠D=∠BAC,∠FAB+∠BAC=∠DCA+∠D,
∴∠FAB=∠DCA.
又AB=CA,∠BFA=∠D,∴△FAB≌△DCA.
∴BF=AD.∴BE=AD.
③④在 中,令y=0,则x=-8;令x=0,则y=6.
∴A(-8,0),C(0,6).∴OA=8,OC=6.
根据勾股定理,得
∵CF=EF,∴∠ECF=∠CEF=∠CAO.∴AE=CE.
如图2,过点 E 作EG⊥AC 于点G,过点 F 作FK⊥CE于点K,FH⊥AB于点H.
②存在、
如图3,设EF 交y轴于点M,过点 F 作FN⊥OA 于点N.
∵点B 与点 A 关于y轴对称,∴OA=OB=8,AC=BC=10.
∴∠FAE=∠EBC.
∵∠CEF=∠CAO,∴∠AFE+∠FEA=∠FEA+∠BEC.
∴∠AFE=∠BEC.
又∠FAE=∠EBC,∴△AFE∽△BEC.∴AE=AEC.
∵△CEF的面积被y轴平分,
∴OA-ON=OB-OE,即AN=BE.
由①,知
由①,知
即
同课章节目录
