2025年中考数学二轮复习专题 2 如何利用“一边一角”构造全等、相似(含答案)
文档属性
| 名称 | 2025年中考数学二轮复习专题 2 如何利用“一边一角”构造全等、相似(含答案) |  | |
| 格式 | docx | ||
| 文件大小 | 335.5KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 通用版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2025-05-29 13:44:00 | ||
图片预览




文档简介
专题 2 如何利用“一边一角”构造全等、相似
难点分解练
核心归纳
编写说明:将此类难题的核心要点总结,结合例题加深理解,之后练综合题目易有解题思路.
类型 何时用 辅助线 解题通法
一 边 一等角 已知一组角相等(∠A=∠D)和一组边(角的 邻边)有数量关系(如 AB=DE) 截取角的另一组边相等(DF=AC),利用“SAS”的方法构造全等(△ABC≌△DEF)、 通过在相等边的另一端点处作一组等角(∠E=∠B).利用“ASA”的方法构造全等(△ABC≌△DEF). 当题目中某个三角形(△ABC)的一个内角(∠BAC)已知(或推导出)与其他角(∠D)相等,且∠BAC 的邻边(或对边)与∠D 的邻边(或对边)有数量关系(已知或所求),那么就以∠D为一个内角,构造一个与∠BAC 所在三角形(△ABC)全等(相似)的三角形,来变换边、角的位置与其他条件组合新的全等、等腰、相似、直角三角形或特殊四边形解决问题.
已知一组角相等(∠BAC=∠D)和一组边 (角的 对边)有数量关系(如 BC =EC) 以有数量关系的边(EC)为腰构造等腰△CEF,得到等角(∠BCA=∠EFD),继而利用“AAS”的方法证明全等(△ABC≌△DEF).
一 边 一互补角 已知一组角互补 ( ∠A ¬∠EDG=180°)和一组边(角的邻边)有数量 关 系 (如AB=DE) 截取角的另一组边相等(DF=AC),利用“SAS”的方法构造全等(△ABC≌△DEF). 通过在相等边的另一端点处作一组等角(∠E=∠B).利用“ASA”的方法构造全等(△ABC≌△DEF). 通过互补角找到等角,再利用一边一等角的思路解题.
类型突破
编写说明:每类例题由浅入深设置,包含该类型的经典情况且在不同几何图形背景下,让学生先练透每个类型,抓住核心本质后再综合练习.
类型1·一边一等角
例1如图,在△ABC中,∠ACB<90°,过点 A 作BC 的平行线AM,D 是 AM 上一点(AD>AC),连接CD,E 是AC的延长线上一点,CD=BE,∠E=∠CDA.求证:AC=BC.
例2.如图,在菱形ABCD 中,对角线AC与 BD 相交于点O,点 E 在 DA 的延长线上,连接OE,将射线OE 绕点O 顺时针旋转∠BCD的度数得到的射线与CD 的延长线相交于点F,探究OE 与 OF 的数量关系.
类型2·一边一互补角
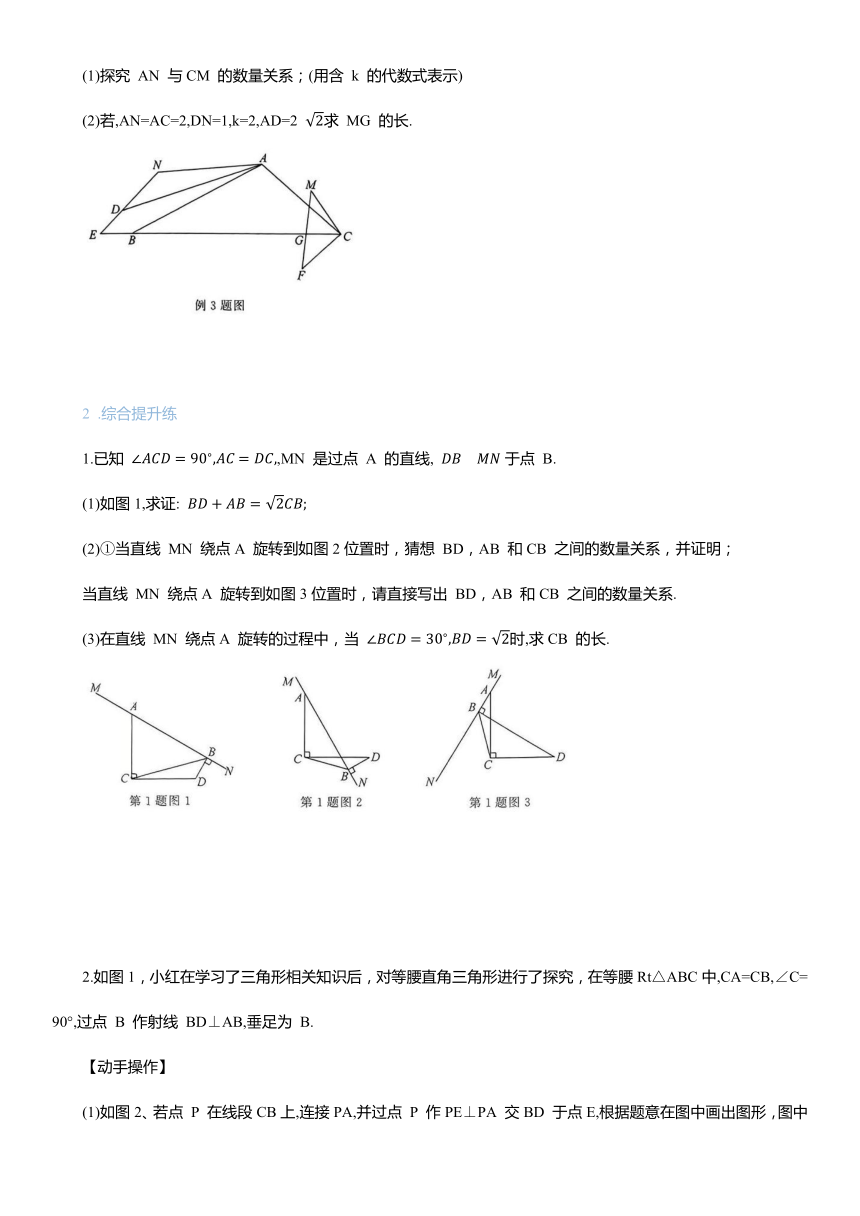
例3如图,△ABC 所在的平面内有一点 D,且AD=AB,E 是CB 的延长线上一点,且ED=EB,F是平面内一点,且AC=kCF,∠ACB=∠FCB,G是BC上一点,且FG=GC,点M,N 分别在 FG和ED的延长线上,连接CM,AN,已知∠M 与∠N 互补.
(1)探究 AN 与CM 的数量关系;(用含 k 的代数式表示)
(2)若,AN=AC=2,DN=1,k=2,AD=2 求 MG 的长.
2 .综合提升练
1.已知 ,MN 是过点 A 的直线, 于点 B.
(1)如图1,求证:
(2)①当直线 MN 绕点A 旋转到如图2位置时,猜想 BD,AB 和CB 之间的数量关系,并证明;
当直线 MN 绕点A 旋转到如图3位置时,请直接写出 BD,AB 和CB 之间的数量关系.
(3)在直线 MN 绕点A 旋转的过程中,当 时,求CB 的长.
2.如图1,小红在学习了三角形相关知识后,对等腰直角三角形进行了探究,在等腰Rt△ABC中,CA=CB,∠C=90°,过点 B 作射线 BD⊥AB,垂足为 B.
【动手操作】
(1)如图2、若点 P 在线段CB上,连接PA,并过点 P 作PE⊥PA 交BD 于点E,根据题意在图中画出图形,图中∠PBE 的度数为 ;
【问题探究】
(2)根据(1)所画图形,探究线段 PA 与EP 之间的数量关系,并说明理由;
【拓展延伸】
(3)如图3、若点 P 在射线CB上移动,过点 P 作PA⊥PE 交BD 于点E,探究线段BA,BP 与BE 之间的数量关系.
3【问题背景】
在 ABCD中,∠ADB=90°,点E 在CD上,点G 在AB 上,点 F 在BD 的延长线上,连接EF,DG
【特例感知】
(1)如图1,当k=1时,试探究AG 与DF 之间的数量关系;
【类比迁移】
(2)如图2,当 时,写出AD,ED 和DF 之间的数量关系,并说明理由;
【问题解决】
(3)在(2)的条件下、当G 是AB 的中点时,连接BE,求 tan∠EBF 的值.
4.在△ABC 中, 的平分线交 AC 于点 D,在AB 的延长线上截取BE,使 BE=CD,连接 DE 交 BC 于点 F.
(1)如图1,当. 时,求 DE 的长;
(2)如图2,当 时,求证:BE=2BF;
(3)如图3、H 是BC的中点,连接AH 分别交DE,BD于点G,K.当AB=6,CD=2时,①求 BC 的长;
直接写出 KG 的长.
5.【问题情境】
数学活动课上,王老师出示了一个问题:
如图1,在△ABC 中,点 D 在AB上,∠ADC=∠ACB.求证:∠ABC=∠ACD.
【独立思考】
(1)请解答王老师的问题;
【实践探究】
(2)在原有问题条件不变的情况下,王老师增加下面的条件,并提出新问题,请你解答.
“如图2、延长CA 至点E,使CE=BD,连接BE,交 CD 的延长线相交于点F,点G,H 分别在BF、BC上,GB=CD、∠BGH=∠BCF.在图中找出与BH 相等的线段,并证明”;
【问题解决】
(3)如图3,在(2)的条件下,
①求证:AC=2AE;
若AB=4,求 BH 的长.
专题2 如何利用“一边一角”构造全等、相似
例1.解:如图,在AE上取一点N,使EN=DA,连接BN.
∵∠E=∠CDA,BE=CD,∴△BEN≌△CDA.
∴BN=CA,∠DAC=∠ENB.
∵AM∥BC,∴∠DAC=∠BCA.∴∠ENB=∠BCA.
∴BN=BC.∴AC=BC.
例2.解:如图,在ED上取一点G,使OG=OD.
∴∠OGD=∠ODG.
∵四边形ABCD 是菱形,∴∠ODG=∠ODC,AD∥BC.
∴∠OGD=∠ODC,∠BCD=∠ADF.
∴∠OGE=∠ODF.
根据旋转的性质,得∠EOF=∠BCD=∠ADF.
∵∠E+∠EOF=∠F+∠ADF,∴∠E=∠F.
又∠OGE=∠ODF,OG=OD,∴△OGE≌△ODF.
∴OE=OF.
例3.解:(1)如图,在EC上取一点 H,使EN=EH,连接AE.
∵AD=AB,ED=EB,AE=AE,
∴△ADE≌△ABE.∴∠AEN=∠AEH.又EN=EH,AE=AE,∴△AEN≌△AEH.
∴∠N=∠AHE,AN=AH.
∵∠N 与∠M互补,∠AHE 与∠AHC 互补,
∴∠M=∠AHC.
∵FG=GC,∠ACB=∠FCB,∴∠F=∠FCB=∠ACB.
∴△AHC∽△CMF∴AHM=ACF=CF=k.
∵AN=AH,∴ANM=k,1即AN=kCM.
(2)如图,过点A 作AK⊥EC于点 K.∴∠AKH=90°.
由题意,得.
由(1)可知,AN=AH=AC=2,EN=EH.
EB,即 DN=BH=1.
∴BK=1+HK.
∵在 Rt△ABK 和 Rt△AHK 中,根据勾股定理, ,
即
解得
∴HC=2HK=3.
∵AC=kCF=2,k=2,∴CF=1.
由(1)可知,∠F=∠FCB=∠ACB,△AHC∽△CMF.
∴∠F=∠FCB=∠ACB=∠AHC,ACF=HC∥=2.
∴△AHC∽△GFC,MF=
即
1.解:(1)证明:如图1,过点 C作CE⊥CB,交MN 于点E、∴∠ACB+∠ACE=90°.
又∠ACD=∠ACB+∠DCB=90°,∴∠ACE=∠DCB、
∵DB⊥MN,∴∠ABD=90°.
∵∠ACD+∠ABD+∠D+∠CAB=360°、
∴∠D+∠CAB=180°.
∵∠EAC+∠CAB=180°,∴∠EAC=∠D.
又AC=DC,∠ACE=∠DCB,∴△ACE≌△DCB、
∴AE=DB,CE=CB.
在Rt△BCE 中,根据勾股定理,得
∵AE+AB=BE,∴BD+AB= CB.
证明:如图2,过点C作CE⊥CB,交 MN于点E.
∴∠ECB=∠ECD+∠DCB=90°.
又∠ACD=∠ECD+∠ACE=90°,∴∠ACE=∠DCB.
∵∠EAC+∠ACD=∠D+∠EBD,∠ACD=∠EBD=90°,
∴∠EAC=∠D.
又AC=DC,∴△ACE≌△DCB.
∴AE=DB,CE=CB.
在 Rt△BCE 中,根据勾股定理,得
∵AB-AE=BE,∴AB-BD= CB.
详解如图3,过点C 作CE⊥CB,交 MN 于点E.
同理①,得△ACE≌△DCB.
∴AE=DB,CE=CB.
在Rt△BCE 中,根据勾股定理,得
∵AE-AB=BE,∴BD-AB= CB.
(3)当C,D 两点在直线MN 异侧时,如图4,过点 C 作CE⊥CB,交 MN 于点E,连接AD.
由(2)①可知,
∵AC=DC,CE=CB,∠ACD=∠ECB=90°,
∴∠CAD=∠CEB=45°,∠ACE=∠BCD=30°.
∴∠EAC=∠CEB-∠ACE=15°.
∴∠BAD=∠CAD-∠EAC=30°.
∴在 Rt△ABD中,
当C,D 两点在直线MN 同侧时,如图5,过点 C 作CE⊥CB,交 MN 于点E,连接AD.
由(1)可知,
同理上种情况得
综上所述,CB的长为 或
2.解:(1)如图1,PE 即为所求.
135°点拨∵∠PAC+∠APC=∠APC+∠EPB,
∴∠PAC=∠EPB.
∵∠BEP+∠EBA=∠PAB+∠APE,∴∠BEP=∠PAB.
∴∠BEP+∠EPB=∠PAB+∠PAC=45°.
∴∠PBE=135°.
(2)PA=EP.理由如下:
如图2,在AC上取一点F,使CP=CF,连接PF.
∵∠C=90°,∴∠PFC=45°,∠PAF+∠APC=90°.
∴∠AFP=135°.
由(1),知∠PBE=135°.∴∠AFP=∠PBE.
∵PA⊥PE,∴∠APE=90°.
∴∠EPB+∠APC=90°.∴∠PAF=∠EPB.
∵CA=CB,CF=CP,∴AF=PB.
又∠PAF=∠EPB,∠AFP=∠PBE,
∴△AFP≌△PBE.∴PA=EP.
(3)当点 P 在线段BC 上时,如图2.
∵CA=CB,∠C=90°,∴∠BAC=∠ABC=45°.
由(2),知∠PFC=45°,△AFP≌△PBE.
当点 P 在线段CB 的延长线上时,如图3,过点 P 作 PG⊥PB 交AB 的延长线于点G.
∵PA⊥PE,∴∠GPB=∠EPA=90°.
∴∠GPB+∠APB=∠EPA+∠APB,即∠GPA=∠BPE.
∵∠ABC=∠PBG=45°,∠GPB=90°,
即
∵∠ABE=90°,∠ABC=45°,∴∠EBP=45°=∠G.
又PB=PG,∠BPE=∠GPA,
∴△BPE≌△GPA.∴BE=GA.
∵GA-BA=BG,∴BE--BA= BP.
综上所述,1 或.
3.解:(1)如图1,在AD上截取DH=ED,连接HG.
当k=1时,AD=BD,DG=EF.
又∠GDH=∠FED,DH=ED,∴△DHG≌△EDF.
∴HG=DF,∠DHG=∠EDF.∴∠AHG=∠BDC.
∵∠ADB=90°,AD=BD,∴∠A=∠ABD=45°.
∵四边形ABCD 是平行四边形,
∴AB∥CD,∴∠CDB=∠ABD=45°.
∴AG=HG=DF.
理由如下:
如图2,在AD 上取一点M,使∠DMG=∠EDF,连接MG.
∴∠AMG=∠CDB.
∵∠GDM=∠FED,∠DMG=∠EDF,∴△GDM∽△FED.
∵四边形ABCD 是平行四边形,∴AB∥CD.
∴∠ABD=∠CDB=∠AMG.
∵∠A=∠A,∴△ABD∽△AMG.
根据勾股定理,得
∵AD=AM+DM,∴AD=2 DF+ ED.
(3)如图2,过点 E 作EN⊥BD 于点 N.
∵∠CDB=∠AMG,∴△EDN∽△AMG.∴AM=MG=ENG.
设 即ED=2x,EN= x.
设DF=m,则MG= m.∴AG=3m.
∵在Rt△ABD中,G是AB的中点,∴DG=AG=3m.
在 Rt△EFN 中,∵根据勾股定理, NF=x+m,
(负值已舍).
∴DF=2x.
∴BD=6x.∴BN=BD-DN=5x.
∴在 Rt△BNE 中.
4.解:(1)如图1,过点 D 作DH⊥AB 于点 H.
∴∠AHD=90°.
∵AC=AB,∠CAB=60°,
∴△ABC 是等边三角形,∠ADH=30°.
∴AB=BC=AC=2.
∵BD平分∠ABC,∴AD=DC=1.
在Rt△ADH 中,∵∠ADH=30°,AD=1,
∵BE=CD=1,∴EH=BH+BE=
在 Rt△DHE中,根据勾股定理,得
(2)如图2、过点 D 作DH∥AB交BC于点H.
∵AB=AC,∴∠C=∠ABC.
∵DH∥AB,∴∠DHC=∠ABC=∠C、∠HDF=∠BEF.∠HDB=∠ABD.∴CD=DH.
∵CD=BE,∴DH=BE.
又∠DFH=∠EFB.∴△DFH≌△EFB.∴HF=BF.
∵BD平分∠ABC,∴∠ABD=∠HBD=∠HDB.
∴DH=BH=BE.∴BE=2BF、
一题多解如图3,过点D作DH∥AB交BC 于点 H,连接EH.
∵AB=AC,∴∠C=∠ABC.
∵DH∥AB,∴∠DHC=∠ABC=∠C.∴CD=DH.
∵CD=BE.∴DH=BE.
又 DH∥AB、∴四边形DBEH 是平行四边形,
∴∠BHE=∠DBH.∠DBA=∠BEH.
∵BD平分∠ABC,
∴∠DBA=∠DBH=∠BHE=∠BEH.
∴BH=BE.∴BE=2BF.
(3)如图4,过点 D 作DM∥AB交BC于点M.
①由(2),得CD=DM=BE=BM,BF=MF.
∵AB=AC=6,CD=2,∴AD=4,BM=2.∴BF=MF=1.
∴CM=1.∴BC=CM+BM=3.
②KG的长为
详解由①,得BC=3,BF=MF=CM=1,BM=2.
∵H是 BC 的中点,AC=AB,∴AH⊥BC,HC=HB=
如图4,过点 D 作DN⊥BC 于点N.
由(2)、得
在 Rt△CND 中,根据勾股定理,得
∵∠DNC=∠AHC=90°,∴GH∥DN.
∴△GHF∽△DNF,△KBH∽△DBN.
5.解:(1)证明:∵∠ADC=∠ACB,
∴∠ABC+∠DCB=∠DCB+∠ACD.
∴∠ABC=∠ACD.
(2)BH=EF.
证明:如图1,在CB上取一点T,使GH=CT,连接DT.
∵GB=CD,∠BGH=∠DCT,∴△BGH≌△DCT.
∴BH=DT,∠GBH=∠CDT.
∵∠CDT+∠FDT=180°,∴∠GBH+∠FDT=180°.
∴∠BFD+∠BTD=180°.
∵∠CFE+∠BFD=180°,∴∠CFE=∠BTD.
又∠ECF=∠DBT,CE=BD,∴△CEF≌△BDT.
∴EF=DT.∴BH=EF.
(3)①由(1),得∠ABC=∠ACD.
∴AB=2AC,AC=2AD.∴AB=4AD.
∴CE=BD=AB-AD=3AD.
∵AE=CE-AC=3AD-2AD=AD,∴AC=2AE.
②∵AB=4,∴AD=AE=1,AC=2.∴BD=EC=3.
在 Rt△ABE 中,根据勾股定理,得
如图2,过点 E 作EM∥AD交CF 的延长线于点M.
∴△ACD∽△ECM,△MEF∽△DBF、
难点分解练
核心归纳
编写说明:将此类难题的核心要点总结,结合例题加深理解,之后练综合题目易有解题思路.
类型 何时用 辅助线 解题通法
一 边 一等角 已知一组角相等(∠A=∠D)和一组边(角的 邻边)有数量关系(如 AB=DE) 截取角的另一组边相等(DF=AC),利用“SAS”的方法构造全等(△ABC≌△DEF)、 通过在相等边的另一端点处作一组等角(∠E=∠B).利用“ASA”的方法构造全等(△ABC≌△DEF). 当题目中某个三角形(△ABC)的一个内角(∠BAC)已知(或推导出)与其他角(∠D)相等,且∠BAC 的邻边(或对边)与∠D 的邻边(或对边)有数量关系(已知或所求),那么就以∠D为一个内角,构造一个与∠BAC 所在三角形(△ABC)全等(相似)的三角形,来变换边、角的位置与其他条件组合新的全等、等腰、相似、直角三角形或特殊四边形解决问题.
已知一组角相等(∠BAC=∠D)和一组边 (角的 对边)有数量关系(如 BC =EC) 以有数量关系的边(EC)为腰构造等腰△CEF,得到等角(∠BCA=∠EFD),继而利用“AAS”的方法证明全等(△ABC≌△DEF).
一 边 一互补角 已知一组角互补 ( ∠A ¬∠EDG=180°)和一组边(角的邻边)有数量 关 系 (如AB=DE) 截取角的另一组边相等(DF=AC),利用“SAS”的方法构造全等(△ABC≌△DEF). 通过在相等边的另一端点处作一组等角(∠E=∠B).利用“ASA”的方法构造全等(△ABC≌△DEF). 通过互补角找到等角,再利用一边一等角的思路解题.
类型突破
编写说明:每类例题由浅入深设置,包含该类型的经典情况且在不同几何图形背景下,让学生先练透每个类型,抓住核心本质后再综合练习.
类型1·一边一等角
例1如图,在△ABC中,∠ACB<90°,过点 A 作BC 的平行线AM,D 是 AM 上一点(AD>AC),连接CD,E 是AC的延长线上一点,CD=BE,∠E=∠CDA.求证:AC=BC.
例2.如图,在菱形ABCD 中,对角线AC与 BD 相交于点O,点 E 在 DA 的延长线上,连接OE,将射线OE 绕点O 顺时针旋转∠BCD的度数得到的射线与CD 的延长线相交于点F,探究OE 与 OF 的数量关系.
类型2·一边一互补角
例3如图,△ABC 所在的平面内有一点 D,且AD=AB,E 是CB 的延长线上一点,且ED=EB,F是平面内一点,且AC=kCF,∠ACB=∠FCB,G是BC上一点,且FG=GC,点M,N 分别在 FG和ED的延长线上,连接CM,AN,已知∠M 与∠N 互补.
(1)探究 AN 与CM 的数量关系;(用含 k 的代数式表示)
(2)若,AN=AC=2,DN=1,k=2,AD=2 求 MG 的长.
2 .综合提升练
1.已知 ,MN 是过点 A 的直线, 于点 B.
(1)如图1,求证:
(2)①当直线 MN 绕点A 旋转到如图2位置时,猜想 BD,AB 和CB 之间的数量关系,并证明;
当直线 MN 绕点A 旋转到如图3位置时,请直接写出 BD,AB 和CB 之间的数量关系.
(3)在直线 MN 绕点A 旋转的过程中,当 时,求CB 的长.
2.如图1,小红在学习了三角形相关知识后,对等腰直角三角形进行了探究,在等腰Rt△ABC中,CA=CB,∠C=90°,过点 B 作射线 BD⊥AB,垂足为 B.
【动手操作】
(1)如图2、若点 P 在线段CB上,连接PA,并过点 P 作PE⊥PA 交BD 于点E,根据题意在图中画出图形,图中∠PBE 的度数为 ;
【问题探究】
(2)根据(1)所画图形,探究线段 PA 与EP 之间的数量关系,并说明理由;
【拓展延伸】
(3)如图3、若点 P 在射线CB上移动,过点 P 作PA⊥PE 交BD 于点E,探究线段BA,BP 与BE 之间的数量关系.
3【问题背景】
在 ABCD中,∠ADB=90°,点E 在CD上,点G 在AB 上,点 F 在BD 的延长线上,连接EF,DG
【特例感知】
(1)如图1,当k=1时,试探究AG 与DF 之间的数量关系;
【类比迁移】
(2)如图2,当 时,写出AD,ED 和DF 之间的数量关系,并说明理由;
【问题解决】
(3)在(2)的条件下、当G 是AB 的中点时,连接BE,求 tan∠EBF 的值.
4.在△ABC 中, 的平分线交 AC 于点 D,在AB 的延长线上截取BE,使 BE=CD,连接 DE 交 BC 于点 F.
(1)如图1,当. 时,求 DE 的长;
(2)如图2,当 时,求证:BE=2BF;
(3)如图3、H 是BC的中点,连接AH 分别交DE,BD于点G,K.当AB=6,CD=2时,①求 BC 的长;
直接写出 KG 的长.
5.【问题情境】
数学活动课上,王老师出示了一个问题:
如图1,在△ABC 中,点 D 在AB上,∠ADC=∠ACB.求证:∠ABC=∠ACD.
【独立思考】
(1)请解答王老师的问题;
【实践探究】
(2)在原有问题条件不变的情况下,王老师增加下面的条件,并提出新问题,请你解答.
“如图2、延长CA 至点E,使CE=BD,连接BE,交 CD 的延长线相交于点F,点G,H 分别在BF、BC上,GB=CD、∠BGH=∠BCF.在图中找出与BH 相等的线段,并证明”;
【问题解决】
(3)如图3,在(2)的条件下,
①求证:AC=2AE;
若AB=4,求 BH 的长.
专题2 如何利用“一边一角”构造全等、相似
例1.解:如图,在AE上取一点N,使EN=DA,连接BN.
∵∠E=∠CDA,BE=CD,∴△BEN≌△CDA.
∴BN=CA,∠DAC=∠ENB.
∵AM∥BC,∴∠DAC=∠BCA.∴∠ENB=∠BCA.
∴BN=BC.∴AC=BC.
例2.解:如图,在ED上取一点G,使OG=OD.
∴∠OGD=∠ODG.
∵四边形ABCD 是菱形,∴∠ODG=∠ODC,AD∥BC.
∴∠OGD=∠ODC,∠BCD=∠ADF.
∴∠OGE=∠ODF.
根据旋转的性质,得∠EOF=∠BCD=∠ADF.
∵∠E+∠EOF=∠F+∠ADF,∴∠E=∠F.
又∠OGE=∠ODF,OG=OD,∴△OGE≌△ODF.
∴OE=OF.
例3.解:(1)如图,在EC上取一点 H,使EN=EH,连接AE.
∵AD=AB,ED=EB,AE=AE,
∴△ADE≌△ABE.∴∠AEN=∠AEH.又EN=EH,AE=AE,∴△AEN≌△AEH.
∴∠N=∠AHE,AN=AH.
∵∠N 与∠M互补,∠AHE 与∠AHC 互补,
∴∠M=∠AHC.
∵FG=GC,∠ACB=∠FCB,∴∠F=∠FCB=∠ACB.
∴△AHC∽△CMF∴AHM=ACF=CF=k.
∵AN=AH,∴ANM=k,1即AN=kCM.
(2)如图,过点A 作AK⊥EC于点 K.∴∠AKH=90°.
由题意,得.
由(1)可知,AN=AH=AC=2,EN=EH.
EB,即 DN=BH=1.
∴BK=1+HK.
∵在 Rt△ABK 和 Rt△AHK 中,根据勾股定理, ,
即
解得
∴HC=2HK=3.
∵AC=kCF=2,k=2,∴CF=1.
由(1)可知,∠F=∠FCB=∠ACB,△AHC∽△CMF.
∴∠F=∠FCB=∠ACB=∠AHC,ACF=HC∥=2.
∴△AHC∽△GFC,MF=
即
1.解:(1)证明:如图1,过点 C作CE⊥CB,交MN 于点E、∴∠ACB+∠ACE=90°.
又∠ACD=∠ACB+∠DCB=90°,∴∠ACE=∠DCB、
∵DB⊥MN,∴∠ABD=90°.
∵∠ACD+∠ABD+∠D+∠CAB=360°、
∴∠D+∠CAB=180°.
∵∠EAC+∠CAB=180°,∴∠EAC=∠D.
又AC=DC,∠ACE=∠DCB,∴△ACE≌△DCB、
∴AE=DB,CE=CB.
在Rt△BCE 中,根据勾股定理,得
∵AE+AB=BE,∴BD+AB= CB.
证明:如图2,过点C作CE⊥CB,交 MN于点E.
∴∠ECB=∠ECD+∠DCB=90°.
又∠ACD=∠ECD+∠ACE=90°,∴∠ACE=∠DCB.
∵∠EAC+∠ACD=∠D+∠EBD,∠ACD=∠EBD=90°,
∴∠EAC=∠D.
又AC=DC,∴△ACE≌△DCB.
∴AE=DB,CE=CB.
在 Rt△BCE 中,根据勾股定理,得
∵AB-AE=BE,∴AB-BD= CB.
详解如图3,过点C 作CE⊥CB,交 MN 于点E.
同理①,得△ACE≌△DCB.
∴AE=DB,CE=CB.
在Rt△BCE 中,根据勾股定理,得
∵AE-AB=BE,∴BD-AB= CB.
(3)当C,D 两点在直线MN 异侧时,如图4,过点 C 作CE⊥CB,交 MN 于点E,连接AD.
由(2)①可知,
∵AC=DC,CE=CB,∠ACD=∠ECB=90°,
∴∠CAD=∠CEB=45°,∠ACE=∠BCD=30°.
∴∠EAC=∠CEB-∠ACE=15°.
∴∠BAD=∠CAD-∠EAC=30°.
∴在 Rt△ABD中,
当C,D 两点在直线MN 同侧时,如图5,过点 C 作CE⊥CB,交 MN 于点E,连接AD.
由(1)可知,
同理上种情况得
综上所述,CB的长为 或
2.解:(1)如图1,PE 即为所求.
135°点拨∵∠PAC+∠APC=∠APC+∠EPB,
∴∠PAC=∠EPB.
∵∠BEP+∠EBA=∠PAB+∠APE,∴∠BEP=∠PAB.
∴∠BEP+∠EPB=∠PAB+∠PAC=45°.
∴∠PBE=135°.
(2)PA=EP.理由如下:
如图2,在AC上取一点F,使CP=CF,连接PF.
∵∠C=90°,∴∠PFC=45°,∠PAF+∠APC=90°.
∴∠AFP=135°.
由(1),知∠PBE=135°.∴∠AFP=∠PBE.
∵PA⊥PE,∴∠APE=90°.
∴∠EPB+∠APC=90°.∴∠PAF=∠EPB.
∵CA=CB,CF=CP,∴AF=PB.
又∠PAF=∠EPB,∠AFP=∠PBE,
∴△AFP≌△PBE.∴PA=EP.
(3)当点 P 在线段BC 上时,如图2.
∵CA=CB,∠C=90°,∴∠BAC=∠ABC=45°.
由(2),知∠PFC=45°,△AFP≌△PBE.
当点 P 在线段CB 的延长线上时,如图3,过点 P 作 PG⊥PB 交AB 的延长线于点G.
∵PA⊥PE,∴∠GPB=∠EPA=90°.
∴∠GPB+∠APB=∠EPA+∠APB,即∠GPA=∠BPE.
∵∠ABC=∠PBG=45°,∠GPB=90°,
即
∵∠ABE=90°,∠ABC=45°,∴∠EBP=45°=∠G.
又PB=PG,∠BPE=∠GPA,
∴△BPE≌△GPA.∴BE=GA.
∵GA-BA=BG,∴BE--BA= BP.
综上所述,1 或.
3.解:(1)如图1,在AD上截取DH=ED,连接HG.
当k=1时,AD=BD,DG=EF.
又∠GDH=∠FED,DH=ED,∴△DHG≌△EDF.
∴HG=DF,∠DHG=∠EDF.∴∠AHG=∠BDC.
∵∠ADB=90°,AD=BD,∴∠A=∠ABD=45°.
∵四边形ABCD 是平行四边形,
∴AB∥CD,∴∠CDB=∠ABD=45°.
∴AG=HG=DF.
理由如下:
如图2,在AD 上取一点M,使∠DMG=∠EDF,连接MG.
∴∠AMG=∠CDB.
∵∠GDM=∠FED,∠DMG=∠EDF,∴△GDM∽△FED.
∵四边形ABCD 是平行四边形,∴AB∥CD.
∴∠ABD=∠CDB=∠AMG.
∵∠A=∠A,∴△ABD∽△AMG.
根据勾股定理,得
∵AD=AM+DM,∴AD=2 DF+ ED.
(3)如图2,过点 E 作EN⊥BD 于点 N.
∵∠CDB=∠AMG,∴△EDN∽△AMG.∴AM=MG=ENG.
设 即ED=2x,EN= x.
设DF=m,则MG= m.∴AG=3m.
∵在Rt△ABD中,G是AB的中点,∴DG=AG=3m.
在 Rt△EFN 中,∵根据勾股定理, NF=x+m,
(负值已舍).
∴DF=2x.
∴BD=6x.∴BN=BD-DN=5x.
∴在 Rt△BNE 中.
4.解:(1)如图1,过点 D 作DH⊥AB 于点 H.
∴∠AHD=90°.
∵AC=AB,∠CAB=60°,
∴△ABC 是等边三角形,∠ADH=30°.
∴AB=BC=AC=2.
∵BD平分∠ABC,∴AD=DC=1.
在Rt△ADH 中,∵∠ADH=30°,AD=1,
∵BE=CD=1,∴EH=BH+BE=
在 Rt△DHE中,根据勾股定理,得
(2)如图2、过点 D 作DH∥AB交BC于点H.
∵AB=AC,∴∠C=∠ABC.
∵DH∥AB,∴∠DHC=∠ABC=∠C、∠HDF=∠BEF.∠HDB=∠ABD.∴CD=DH.
∵CD=BE,∴DH=BE.
又∠DFH=∠EFB.∴△DFH≌△EFB.∴HF=BF.
∵BD平分∠ABC,∴∠ABD=∠HBD=∠HDB.
∴DH=BH=BE.∴BE=2BF、
一题多解如图3,过点D作DH∥AB交BC 于点 H,连接EH.
∵AB=AC,∴∠C=∠ABC.
∵DH∥AB,∴∠DHC=∠ABC=∠C.∴CD=DH.
∵CD=BE.∴DH=BE.
又 DH∥AB、∴四边形DBEH 是平行四边形,
∴∠BHE=∠DBH.∠DBA=∠BEH.
∵BD平分∠ABC,
∴∠DBA=∠DBH=∠BHE=∠BEH.
∴BH=BE.∴BE=2BF.
(3)如图4,过点 D 作DM∥AB交BC于点M.
①由(2),得CD=DM=BE=BM,BF=MF.
∵AB=AC=6,CD=2,∴AD=4,BM=2.∴BF=MF=1.
∴CM=1.∴BC=CM+BM=3.
②KG的长为
详解由①,得BC=3,BF=MF=CM=1,BM=2.
∵H是 BC 的中点,AC=AB,∴AH⊥BC,HC=HB=
如图4,过点 D 作DN⊥BC 于点N.
由(2)、得
在 Rt△CND 中,根据勾股定理,得
∵∠DNC=∠AHC=90°,∴GH∥DN.
∴△GHF∽△DNF,△KBH∽△DBN.
5.解:(1)证明:∵∠ADC=∠ACB,
∴∠ABC+∠DCB=∠DCB+∠ACD.
∴∠ABC=∠ACD.
(2)BH=EF.
证明:如图1,在CB上取一点T,使GH=CT,连接DT.
∵GB=CD,∠BGH=∠DCT,∴△BGH≌△DCT.
∴BH=DT,∠GBH=∠CDT.
∵∠CDT+∠FDT=180°,∴∠GBH+∠FDT=180°.
∴∠BFD+∠BTD=180°.
∵∠CFE+∠BFD=180°,∴∠CFE=∠BTD.
又∠ECF=∠DBT,CE=BD,∴△CEF≌△BDT.
∴EF=DT.∴BH=EF.
(3)①由(1),得∠ABC=∠ACD.
∴AB=2AC,AC=2AD.∴AB=4AD.
∴CE=BD=AB-AD=3AD.
∵AE=CE-AC=3AD-2AD=AD,∴AC=2AE.
②∵AB=4,∴AD=AE=1,AC=2.∴BD=EC=3.
在 Rt△ABE 中,根据勾股定理,得
如图2,过点 E 作EM∥AD交CF 的延长线于点M.
∴△ACD∽△ECM,△MEF∽△DBF、
同课章节目录
