2025年中考数学二轮复习函数重难选填题:专题2 函数解析式的应用(含答案)
文档属性
| 名称 | 2025年中考数学二轮复习函数重难选填题:专题2 函数解析式的应用(含答案) |  | |
| 格式 | docx | ||
| 文件大小 | 106.5KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 通用版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2025-05-29 13:45:53 | ||
图片预览


文档简介
专题2 函数解析式的应用
类型1·代几综合
1.如图,直线y= kx+b(k≠0)与x轴相交于点A(3,0),与y轴相交于点 B(0,6),若在线段AB上存在一点 M,使得∠AMO=45°,则点 M 的坐标是 .
2.2024辽宁省模如图,抛物线 与 x 轴相交于 A,B两点.点C 的坐标为( ,0),.点 P 在抛物线上,将线段 PC 绕点 P 顺时针旋转90°得到线段 PD,当点 D 落在 y 轴正半轴上时,点D 的坐标为 、
3.如图,抛物线 与x轴相交于点 A,B,与y轴相交于点 C,P是抛物线上一点,连接AC,BP,若∠ABP=∠CAO,则点 P 的坐标为 .
4.2024大连模拟如图,在平面直角坐标系中,抛物线 与x轴相交于点A,B,与y轴相交于点C,点D 在线段OC上,坐标为(0,m),点E 的坐标为(2m,0),过点 E 作x轴的垂线l,点D 关于直线l的对称点为点D',连接DE,D'E.若D'E与抛物线有一个公共点,则m的取值范围是 .
类型2·实际应用
5.2024鞍山二模如图,小明站在原点处,从离地面高度为1m 的点 A 处抛出弹力球,弹力球在B 处着地后弹起,落至点C处,弹力球着地前后的运动轨迹可近似看成形状相同的两条抛物线,弹力球第一次着地前抛物线的解析式为. ,弹力球在点 B 处着地后弹起的最大高度为着地前抛出的最大高度的一半,在地上摆放一个底面半径为0.5m,高为0.5m 的圆柱形筐,筐的最左端距离原点为 nm,若要弹力球从点 B 弹起后落入筐内,则n的值可以是 ( )
A.7 B.9 C.10 D.8
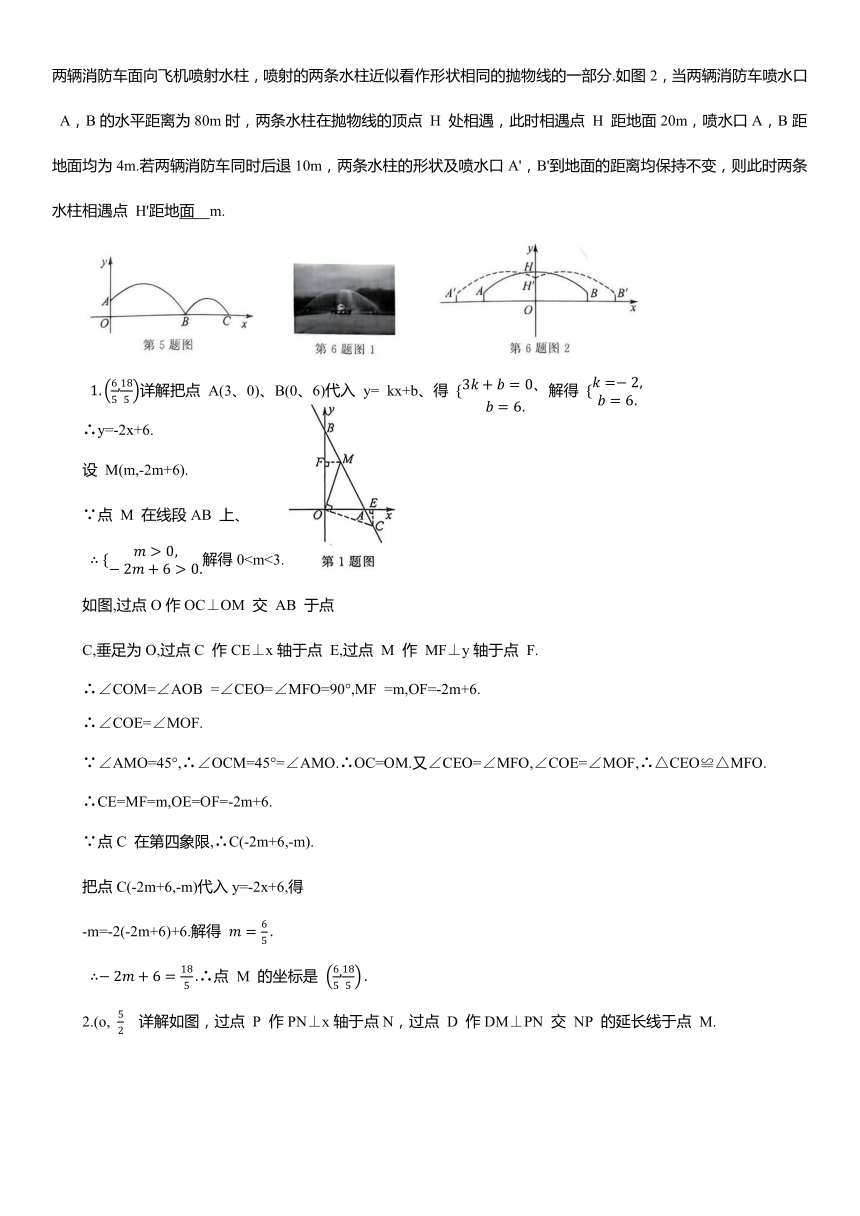
6.2023年5月28日,C919商业首航完成——中国民商业运营国产大飞机正式起步.12时31分航班抵达北京首都机场,穿过隆重的“水门礼”(寓意“接风洗尘”,是国际民航中最高级别的礼仪).如图1,在一次“水门礼”的预演中,两辆消防车面向飞机喷射水柱,喷射的两条水柱近似看作形状相同的抛物线的一部分.如图2,当两辆消防车喷水口 A,B的水平距离为80m时,两条水柱在抛物线的顶点 H 处相遇,此时相遇点 H 距地面20m,喷水口A,B距地面均为4m.若两辆消防车同时后退10m,两条水柱的形状及喷水口A',B'到地面的距离均保持不变,则此时两条水柱相遇点 H'距地面 m.
详解把点 A(3、0)、B(0、6)代入 y= kx+b、得 解得
∴y=-2x+6.
设 M(m,-2m+6).
∵点 M 在线段AB 上、
解得0如图,过点O作OC⊥OM 交 AB 于点
C,垂足为O,过点C 作CE⊥x轴于点 E,过点 M 作 MF⊥y轴于点 F.
∴∠COM=∠AOB =∠CEO=∠MFO=90°,MF =m,OF=-2m+6.
∴∠COE=∠MOF.
∵∠AMO=45°,∴∠OCM=45°=∠AMO.∴OC=OM.又∠CEO=∠MFO,∠COE=∠MOF,∴△CEO≌△MFO.
∴CE=MF=m,OE=OF=-2m+6.
∵点C 在第四象限,∴C(-2m+6,-m).
把点C(-2m+6,-m)代入y=-2x+6,得
-m=-2(-2m+6)+6.解得
∴点 M 的坐标是
2.(o, 详解如图,过点 P 作PN⊥x轴于点N,过点 D 作DM⊥PN 交 NP 的延长线于点 M.
∴∠M=∠PNC=90°.∴∠MDP+∠DPM=90°.
∵将线段 PC 绕点 P 顺时针旋转90°得到线段 PD,点 D 落在y轴正半轴上,
∴DP=PC,∠DPC=90°,点 P 在第一象限的抛物线上.
∴∠NPC+∠DPM=90°.∴∠MDP=∠NPC.又DP=PC,∠M=∠PNC,∴△MDP≌△NPC.
∴DM=PN,MP=NC.
设
解得 (不合题意,舍去),,m =2.∴N(2,0),PN=2.
3.(-4,-21)或(2,3)详解当点 P 在x轴下方的抛物线上时,如图,过点 B 作 BE∥AC交y轴于点 E,交抛物线于点 P.
∴∠CAO=∠ABP.
令x=0,则y=3.
令y=0,则
解得
∴A(--1,0),B(3,0),C(0,3).
∴OA=1,OB=3,OC=3.
∴OE=9.∴E(0,-9).
设 BE 所在直线的函数解析式为y=kx+b.
将点 B(3,0),E(0,-9)代入y= kx+b,得
解得
联立 解得
∴P(-4,-21).
当点 P 在x 轴上方的抛物线上时,记为点 P',如图,作点 E关于x轴的对称点 E',直线 BE'交抛物线于点 P'.
由对称的性质,得
∵E(0,-9),∴E'(0,9).
同理可得,直线 BE'的函数解析式为y=-3x+9.
联立 解得
∴P'(2,3).
综上所述,点 P 的坐标为(-4,-21)或(2,3).
详解当x=0时,y=2.∴C(0,2).
∵点 D(0,m)在OC 上,∴0≤m≤2.
∵点 D 的坐标为(0,m),点 E 的坐标为(2m,0),
∴点 D 关于直线l的对称点 D'的坐标为(4m,m).
∵D'E与抛物线有一个公共点,
令
当 时,
解得
如图为函数y 的图象,当 时、y ≥0.
的解集为
同理,得 的解集为m≤ 或
∴m 的取值范围是
5. D详解 把点A(0,1)代入 得
解得
∴当x=2时,y最大,最大值为2.
令y=0,则
解得 不合题意,舍去).(
∵弹力球在点 B 处着地后弹起的最大高度为着地前抛出的最大高度的一半,∴其最大高度为
∵弹力球着地前后的运动轨迹可近似看成形状相同的两条抛物线,
∴设着地后弹起的抛物线解析式为
把点 代入,得
解得 (不合题意,舍去).
∴该抛物线的解析式为
∴对称轴为直线
∵点 B 的坐标为 点C的坐标为(
∵圆柱形的高为0.5m ,
∴把y=0.5代入 得
解得 (不合题意,舍去).
∴当弹力球恰好砸中筐的最左端时,
∵筐的底面半径为0.5m ,即直径为 1m ,
∴当弹力球恰好砸中筐的最右端时,
∴选项 D:n=8满足.故选 D.
6.19详解由题意可知A(-40,4),B(40,4),H(0,20).
∴设抛物线的解析式为
把点A(-40,4)代入 得 解得
∵两辆消防车同时后退10 m,即抛物线 向左(右)平移10m,
∴平移后抛物线的解析式为 或y=
令x=0.解得y=19.
类型1·代几综合
1.如图,直线y= kx+b(k≠0)与x轴相交于点A(3,0),与y轴相交于点 B(0,6),若在线段AB上存在一点 M,使得∠AMO=45°,则点 M 的坐标是 .
2.2024辽宁省模如图,抛物线 与 x 轴相交于 A,B两点.点C 的坐标为( ,0),.点 P 在抛物线上,将线段 PC 绕点 P 顺时针旋转90°得到线段 PD,当点 D 落在 y 轴正半轴上时,点D 的坐标为 、
3.如图,抛物线 与x轴相交于点 A,B,与y轴相交于点 C,P是抛物线上一点,连接AC,BP,若∠ABP=∠CAO,则点 P 的坐标为 .
4.2024大连模拟如图,在平面直角坐标系中,抛物线 与x轴相交于点A,B,与y轴相交于点C,点D 在线段OC上,坐标为(0,m),点E 的坐标为(2m,0),过点 E 作x轴的垂线l,点D 关于直线l的对称点为点D',连接DE,D'E.若D'E与抛物线有一个公共点,则m的取值范围是 .
类型2·实际应用
5.2024鞍山二模如图,小明站在原点处,从离地面高度为1m 的点 A 处抛出弹力球,弹力球在B 处着地后弹起,落至点C处,弹力球着地前后的运动轨迹可近似看成形状相同的两条抛物线,弹力球第一次着地前抛物线的解析式为. ,弹力球在点 B 处着地后弹起的最大高度为着地前抛出的最大高度的一半,在地上摆放一个底面半径为0.5m,高为0.5m 的圆柱形筐,筐的最左端距离原点为 nm,若要弹力球从点 B 弹起后落入筐内,则n的值可以是 ( )
A.7 B.9 C.10 D.8
6.2023年5月28日,C919商业首航完成——中国民商业运营国产大飞机正式起步.12时31分航班抵达北京首都机场,穿过隆重的“水门礼”(寓意“接风洗尘”,是国际民航中最高级别的礼仪).如图1,在一次“水门礼”的预演中,两辆消防车面向飞机喷射水柱,喷射的两条水柱近似看作形状相同的抛物线的一部分.如图2,当两辆消防车喷水口 A,B的水平距离为80m时,两条水柱在抛物线的顶点 H 处相遇,此时相遇点 H 距地面20m,喷水口A,B距地面均为4m.若两辆消防车同时后退10m,两条水柱的形状及喷水口A',B'到地面的距离均保持不变,则此时两条水柱相遇点 H'距地面 m.
详解把点 A(3、0)、B(0、6)代入 y= kx+b、得 解得
∴y=-2x+6.
设 M(m,-2m+6).
∵点 M 在线段AB 上、
解得0
C,垂足为O,过点C 作CE⊥x轴于点 E,过点 M 作 MF⊥y轴于点 F.
∴∠COM=∠AOB =∠CEO=∠MFO=90°,MF =m,OF=-2m+6.
∴∠COE=∠MOF.
∵∠AMO=45°,∴∠OCM=45°=∠AMO.∴OC=OM.又∠CEO=∠MFO,∠COE=∠MOF,∴△CEO≌△MFO.
∴CE=MF=m,OE=OF=-2m+6.
∵点C 在第四象限,∴C(-2m+6,-m).
把点C(-2m+6,-m)代入y=-2x+6,得
-m=-2(-2m+6)+6.解得
∴点 M 的坐标是
2.(o, 详解如图,过点 P 作PN⊥x轴于点N,过点 D 作DM⊥PN 交 NP 的延长线于点 M.
∴∠M=∠PNC=90°.∴∠MDP+∠DPM=90°.
∵将线段 PC 绕点 P 顺时针旋转90°得到线段 PD,点 D 落在y轴正半轴上,
∴DP=PC,∠DPC=90°,点 P 在第一象限的抛物线上.
∴∠NPC+∠DPM=90°.∴∠MDP=∠NPC.又DP=PC,∠M=∠PNC,∴△MDP≌△NPC.
∴DM=PN,MP=NC.
设
解得 (不合题意,舍去),,m =2.∴N(2,0),PN=2.
3.(-4,-21)或(2,3)详解当点 P 在x轴下方的抛物线上时,如图,过点 B 作 BE∥AC交y轴于点 E,交抛物线于点 P.
∴∠CAO=∠ABP.
令x=0,则y=3.
令y=0,则
解得
∴A(--1,0),B(3,0),C(0,3).
∴OA=1,OB=3,OC=3.
∴OE=9.∴E(0,-9).
设 BE 所在直线的函数解析式为y=kx+b.
将点 B(3,0),E(0,-9)代入y= kx+b,得
解得
联立 解得
∴P(-4,-21).
当点 P 在x 轴上方的抛物线上时,记为点 P',如图,作点 E关于x轴的对称点 E',直线 BE'交抛物线于点 P'.
由对称的性质,得
∵E(0,-9),∴E'(0,9).
同理可得,直线 BE'的函数解析式为y=-3x+9.
联立 解得
∴P'(2,3).
综上所述,点 P 的坐标为(-4,-21)或(2,3).
详解当x=0时,y=2.∴C(0,2).
∵点 D(0,m)在OC 上,∴0≤m≤2.
∵点 D 的坐标为(0,m),点 E 的坐标为(2m,0),
∴点 D 关于直线l的对称点 D'的坐标为(4m,m).
∵D'E与抛物线有一个公共点,
令
当 时,
解得
如图为函数y 的图象,当 时、y ≥0.
的解集为
同理,得 的解集为m≤ 或
∴m 的取值范围是
5. D详解 把点A(0,1)代入 得
解得
∴当x=2时,y最大,最大值为2.
令y=0,则
解得 不合题意,舍去).(
∵弹力球在点 B 处着地后弹起的最大高度为着地前抛出的最大高度的一半,∴其最大高度为
∵弹力球着地前后的运动轨迹可近似看成形状相同的两条抛物线,
∴设着地后弹起的抛物线解析式为
把点 代入,得
解得 (不合题意,舍去).
∴该抛物线的解析式为
∴对称轴为直线
∵点 B 的坐标为 点C的坐标为(
∵圆柱形的高为0.5m ,
∴把y=0.5代入 得
解得 (不合题意,舍去).
∴当弹力球恰好砸中筐的最左端时,
∵筐的底面半径为0.5m ,即直径为 1m ,
∴当弹力球恰好砸中筐的最右端时,
∴选项 D:n=8满足.故选 D.
6.19详解由题意可知A(-40,4),B(40,4),H(0,20).
∴设抛物线的解析式为
把点A(-40,4)代入 得 解得
∵两辆消防车同时后退10 m,即抛物线 向左(右)平移10m,
∴平移后抛物线的解析式为 或y=
令x=0.解得y=19.
同课章节目录
