2025年中考数学二轮复习函数重难选填题:专题1 几何动态问题中函数图象的判断与分析(含答案)
文档属性
| 名称 | 2025年中考数学二轮复习函数重难选填题:专题1 几何动态问题中函数图象的判断与分析(含答案) |

|
|
| 格式 | docx | ||
| 文件大小 | 459.1KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 通用版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2025-05-29 00:00:00 | ||
图片预览



文档简介
专题1 几何动态问题中函数图象的判断与分析
类型1·函数图象的判断
考向 1:单个图形的面积问题
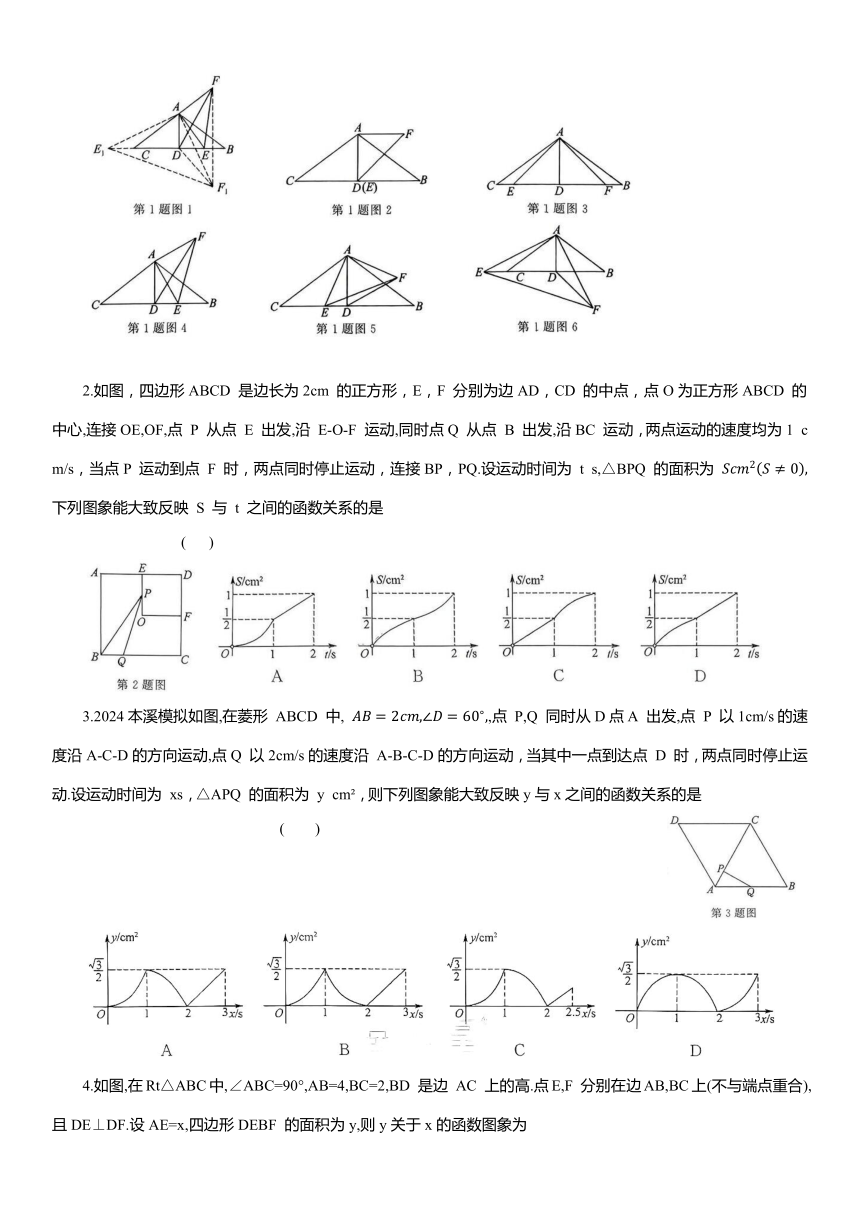
1.如图,在等腰△ABC中,AD为中线,AB=AC=5,BC=8,E 是射线BC上一点(不与点 D 重合),连接AE,将线段AE 绕点 A 逆时针旋转90°得到线段AF,连接 EF,DF.设BE的长为x,△DEF 的面积为y,则下列图象能大致反映y与x之间函数关系的是 ( )
思路引导 以此题为例,将本专题题目的核心分析过程(注意黑色加粗字)分解成一个个小问呈现,助梳理解题思路.
(1)审题得基本信息:①谁在动: ;从哪往哪动: ;③动了多长: .
(2)根据运动过程确定状态图和界点图:①先画出初状态和末状态:初状态为点E 从点B 出发一小段时的位置,末状态为点E 在BC的延长线上(如图1),观察△DEF 运动到△DE F ;根据初末状态确定临界点(此点前后图形状态不同):D是定点,点E 运动到点E 是从点 D 的右侧运动到点D 的左侧,所以点 E 与点D重合时是一个临界点,画出界点图,如图2,这时x= .点F 运动到点F 时,点F 从DE 的上方运动到DE 的下方,所以点 F 落在直线DE 上时是一个临界点,画出界点图,如图3,这时x= ;③根据界点图画出临界点前后的状态图:当点E 在BD 上,点F 在DE 上方时,如图4;当点E 在BD 的延长线上,点F 在DE 上方时,如图5;当点E 在BD 的延长线上,点 F 在DE 下方时,如图6.
(3)面积计算:一般两种方法,①几何图形面积公式:底、高是定长或可以用含x的代数式表示.常用求线段长的方法有:同一直线上和差,把线段放在几何图形中利用全等、相似、勾股定理来求线段长;用面积的和差:当所求几何图形的底和高不容易用含x的代数式表示线段长时,或所求几何图形是不规则几何图形时,可以把所求的几何图形转换成其他几何图形的和差,利用其他几何图形的面积来求.
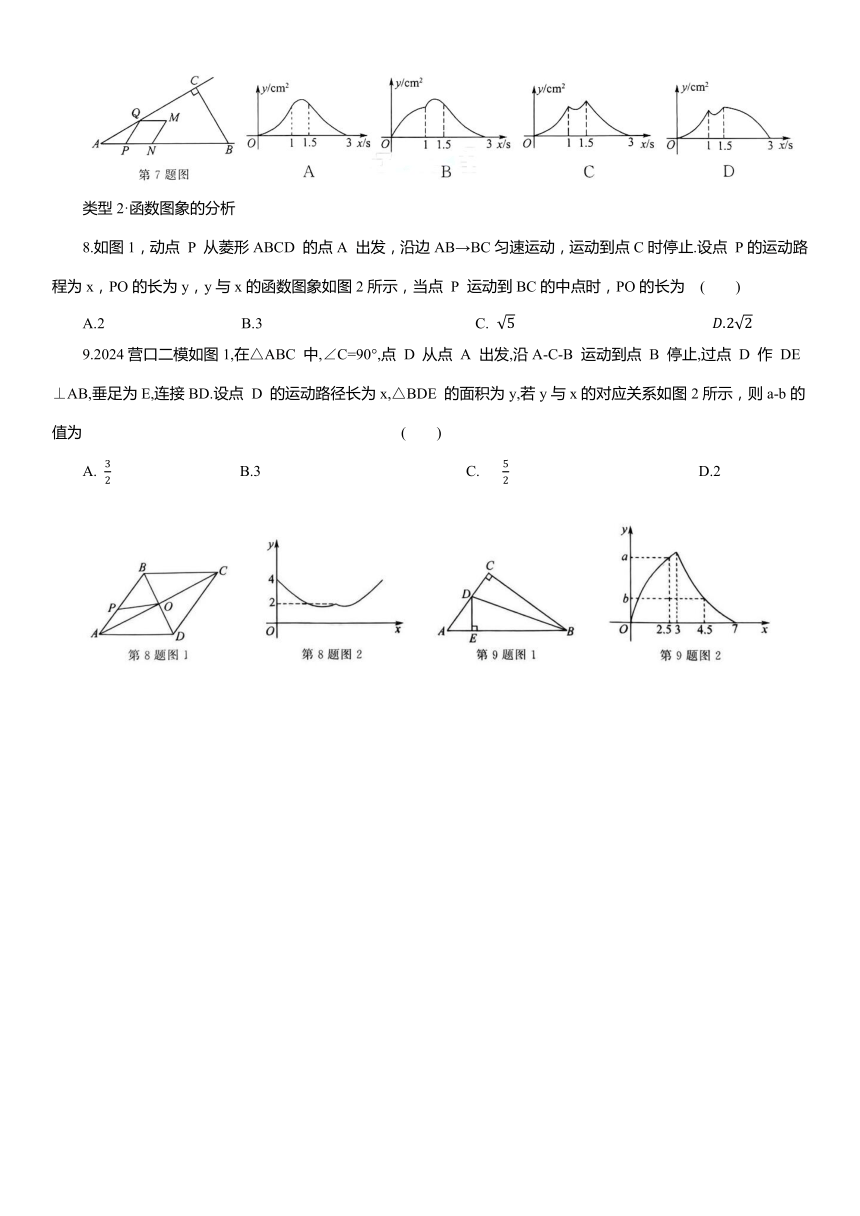
2.如图,四边形ABCD 是边长为2cm 的正方形,E,F 分别为边AD,CD 的中点,点O为正方形ABCD 的中心,连接OE,OF,点 P 从点 E 出发,沿 E-O-F 运动,同时点Q 从点 B 出发,沿BC 运动,两点运动的速度均为1 cm/s,当点P 运动到点 F 时,两点同时停止运动,连接BP,PQ.设运动时间为 t s,△BPQ 的面积为 下列图象能大致反映 S 与 t 之间的函数关系的是 ( )
3.2024本溪模拟如图,在菱形 ABCD 中, ,点 P,Q 同时从D点A 出发,点 P 以1cm/s的速度沿A-C-D的方向运动,点Q 以2cm/s的速度沿 A-B-C-D的方向运动,当其中一点到达点 D 时,两点同时停止运动.设运动时间为 xs,△APQ 的面积为 y cm ,则下列图象能大致反映y与x之间的函数关系的是 ( )
4.如图,在Rt△ABC中,∠ABC=90°,AB=4,BC=2,BD 是边 AC 上的高.点E,F 分别在边AB,BC上(不与端点重合),且DE⊥DF.设AE=x,四边形DEBF 的面积为y,则y关于x的函数图象为 ( )
考向 2:图形重叠的面积问题
5.如图,在Rt△ABC中,∠ABC=90°,AB=2BC=4,动点 P 从点 A 出发,以每秒1个单位长度的速度沿线段 AB 匀速运动,当点 P 运动到点 B 时,停止运动,过点 P 作 交AC于点Q,将△APQ 沿直线PQ 折叠得到△A'PQ.设动点 P 的运动时间为 ts,△A'PQ与 重叠部分的面积为S,则下列图象能大致反映 S 与t之间的函数关系的是 ( )
6.2023锦州中考如图,在Rt△ABC 中,∠ACB=90°,AC=3,BC=4,在△DEF 中,DE=DF=5,EF=8,BC 与EF 在同一条直线上,点 C 与点 E 重合.△ABC 以每秒1个单位长度的速度沿线段EF 所在直线向右匀速运动,当点 B 运动到点 F 时,△ABC 停止运动.设运动时间为 ts,△ABC 与△DEF 重叠部分的面积为S,则下列图象能大致反映S与t之间的函数关系的是( )
7.2023本溪铁岭辽阳中考如图,在Rt△ABC中,∠ACB=90°,∠A=30°,AB=3cm.动点 P 从点 A出发,以1 cm/s的速度沿射线AB 匀速运动,到点B 停止运动,同时动点Q 从点A 出发,以 的速度沿射线AC 匀速运动.当点 P 停止运动时,点Q 也随之停止运动.在PQ 的右侧以PQ 为边作菱形 PQMN,点 N 在射线 AB 上.设点 P 的运动时间为x s,菱形 PQMN 与△ABC 重叠部分的面积为ycm ,则下列图象能大致反映y 与x之间的函数关系的是 ( )
类型2·函数图象的分析
8.如图1,动点 P 从菱形ABCD 的点A 出发,沿边AB→BC匀速运动,运动到点C时停止.设点 P的运动路程为x,PO的长为y,y与x的函数图象如图2所示,当点 P 运动到BC的中点时,PO的长为 ( )
A.2 B.3 C.
9.2024营口二模如图1,在△ABC 中,∠C=90°,点 D 从点 A 出发,沿A-C-B 运动到点 B 停止,过点 D 作 DE⊥AB,垂足为E,连接BD.设点 D 的运动路径长为x,△BDE 的面积为y,若y与x的对应关系如图2所示,则a-b的值为 ( )
A. B.3 C. D.2
专题 1 几何动态问题中函数图象的判断与分析
1. C思路引导(1)点 E;从点 B 沿射线 BC 动;x (2)4;7
详解∵AB=AC=5,BC=8,AD为中线,
∴AD⊥BC,CD=BD=4.
在 Rt△ABD 中,根据勾股定理,得. 当点E 与点D 重合时,如图1,BE=4.
当点 F 在BC 上时,如图2,由旋转的性质,得 AE=AF,∠EAF=90°.
又AD⊥BC,∴ED=FD.∴AD=ED=FD=3.
∴BE=ED+BD=7.
①当0≤x<4 时,如图3,过点 F 分别作 FH⊥DA 交DA的延长线于点 H,FG⊥BD 于点G.
∴∠H=∠FGE=∠ADE=90°.
∴∠HAF+∠HFA=90°,四边形 HDGF 为矩形.
∴HD=FG.
∵∠FAE=90°,∴∠HAF+∠DAE=90°.
∴∠HFA=∠DAE.
又∠H=∠ADE=90°,AF=AE,∴△HAF≌△DEA.
∴FH=AD=3,HA=DE=BD--BE=4-x.
∴FG=HD=HA+AD=7-x.
故 A,B选项不正确.
当4≤x<7时,如图4,过点 F 作FM⊥AD 于点M.
同理①,得△AMF≌△EDA.
∴AM=ED=x-4,MF=DA=3.
∴MD=AD-AM=3-(x-4)=7-x.
③当x≥7时,如图5,过点 F 作FN⊥AD 交AD 的延长线于点 N.
同理①,得△AED≌△FAN.
∴AD=FN=3,ED=AN=x-4.
∴DN=AN-AD=x-4-3=x-7.
故D选项不正确.故选 C.
2. D 详解根据题意,得四边形 EOFD 为正方形,OE=OF=1.
当0∴点 P 到直线BC 的距离为2-t.
故 A,C选项不正确.
当1故B选项不正确.故选 D.
3. A 详解∵四边形 ABCD 是菱形,
∴AB=BC=CD=AD=2,∠B=∠D=60°.
∴△ABC 和△ACD 都是等边三角形.
∴∠CAB=∠ACB=∠ACD=60°.
如图1,过点 C 作CM⊥AB 于点 M、
∴∠BMC=90°.∴CM=BC· sin 60°=
当0≤x≤1时,如图2,过点 P 作PE⊥AB 于点 E、
∴∠AEP=90°.此时AQ=2x、AP=x、
故D选项不正确.
当1此时CP=2-x,CQ=4-2x,BQ=2x-2.
故 B选项不正确.
当2∴∠AGC=90°.∴AG=AC· sin 60°=
此时CP=x-2,CQ=2x-4.∴PQ=x-2.
故 C 选项不正确.故选 A.
4. A 详解如图,过点 D作 DH⊥AB 于点 H.∴∠DHA=90°.
在 Rt△ABC 中,根据勾股定理,得 ∵BD 是边AC上的高,
在 Rt△BCD 中,根据勾股定理,得
∵DE⊥DF,BD⊥AC,∴∠EDF=∠BDC=∠ABC=90°.
∴∠BDE = 90°-∠BDF = ∠CDF,∠DBE = 90°-∠CBD=∠C.
∴△BDE∽△CDF.
∴y随x的增大而减小,且 y与x的函数图象为线段(不含端点).
观察各选项图象可知,A符合题意.故选 A.
5. D 详解∵∠ABC=90°,AB=2BC=4,∴tanA= 由题意,知AP=l.
∵PQ⊥AB,∴∠APQ=90°.∴PQ=AP·tanA=
由折叠的性质,得A'P=AP=t,∠APQ=∠A'PQ=90°.当点 P 与AB 中点重合时,AP+A'P=AB=4.∴t=2.当点 P 在AB 中点的左侧,即0≤t<2时,
△A'PQ与△ABC 重叠部分的面积为
故 A,C选项不正确.
当点 P 在AB 中点的右侧,即2≤t≤4时,如图.
由折叠的性质,得.A'P=AP=t,∠APQ=∠A'PQ=90°,
∴△A'PQ 与△ABC 重叠部分的面积为 故B选项不正确.故选 D.
6. A 详解如图1,过点 D 作DH⊥EF 于点 H.
∴∠DHE=90°.
∵DE=DF=5,EF=8,
在 Rt△DHE 中,根据勾股定理,得
在 Rt△ABC 中,根据勾股定理,得
∵AB=DE=5,BC=EH=4,AC=DH=3,
∴△ABC≌△DEH.∴∠B=∠DEH=∠F.
①当0≤t<4时,如图2,设AC 与DE 相交于点M.
故 B,D选项不正确.
②当4≤t≤8时,如图 3,设 AB 交 DF 于点M,AC 交 DF于点N,过点 M 作MH⊥AC 于点 H.
∵CE=t,∴CF=8-t.
∵∠ACB=90°,∴∠ABC+∠A=∠F+∠CNF=90°.
∵∠ABC=∠F,∴∠A=∠CNF=∠MNH.∴MA=MN.
故C选项不正确.故选 A.
7. A详解∵∠ACB=90°,∠A=30°,AB=3,
如图1,过点 P 作PD⊥AC于点 D,过点 Q 作QE⊥AB 于点E.∴∠ADP=∠PEQ=90°.
由题意,得AP=x,AQ= x.
∴PD 是线段AQ 的垂直平分线.
∴∠PQA=∠A=30°,PQ=AP=x.∴∠QPE=60°.
∵四边形 PQMN 是菱形,
∴PQ=PN=MN=QM=x,PQ∥MN.
∴∠MNB=∠QPE=60°.
当点 M 运动到直线 BC 上时,如图2.
∵四边形 PQMN 是菱形,∴QM∥PN.
∴∠A=∠CQM=30°.
又
解得x=1、
当点 Q 运动到与点C 重合时,如图3、
∵∠A=∠AQP=30°,∴∠PQB=∠PBQ=60°、
∴PQ=PB.∴此时点 N 与点B 重合、
当点 P 运动到与点B 重合时,AP=AB=3.∴x=3.
当0≤x≤1时,
故B选项不正确.
当 时,如图4,过点 F 作 FG⊥AB 于点G,GF 的延长线交 QM 于点 R,设QM 交 BC 于点 S.∴∠FGN=90°.
∵∠FNB=∠CBA=60°,QM∥PN,
∴∠NFB =∠SFM =∠M =∠FSM = 60°,∠FRM =∠FGN=90°.
∴△NFB 和△SFM 均是等边三角形.
∴BN=NF=AB-AP-PN=3-2x.
∴FM=SM=MN-NF=3x-3.
当 时,如图5,设 PQ 交 BC 于点 H,过点 H 作HI⊥AB 于点1、
∴∠HIB=90°.同理可得△PHB 是等边三角形.
∵y=S△PHB,
故选 A.
8. C详解根据图象,得当x=0时,PO=AO=4.
当点 P 运动到点 B 时,PO=BO=2.
∵四边形ABCD 是菱形,∴AB=BC,∠AOB=∠BOC=90°.
在 Rt△AOB 中,根据勾股定理,得
∵P 为BC 的中点, 故选 C.
9. D详解由函数图象的拐点,得AC=3,AC+BC=7.
在 Rt△ABC 中,根据勾股定理,得
当y=a,x=AD=2.5时,点D 在AC上,如图1.
∵DE⊥AB,∴∠DEA=∠BED=90°.
∵∠A=∠A,∠DEA=∠C=90°,∴△ADE∽△ABC.
即
∴DE=2,AE=1.5.∴BE=AB-AE=3.5.
即a=3.5.
当y=b,x=4.5时,点 D 在BC上,如图2.
∵AC+BC=7,AC+CD=4.5,∴BD=2.5.
∵∠B=∠B,∠BED=∠C=90°,∴△BDE∽△BAC.
即
即b=1.5.
∴α-b=3.5-1.5=2.故选 D.
类型1·函数图象的判断
考向 1:单个图形的面积问题
1.如图,在等腰△ABC中,AD为中线,AB=AC=5,BC=8,E 是射线BC上一点(不与点 D 重合),连接AE,将线段AE 绕点 A 逆时针旋转90°得到线段AF,连接 EF,DF.设BE的长为x,△DEF 的面积为y,则下列图象能大致反映y与x之间函数关系的是 ( )
思路引导 以此题为例,将本专题题目的核心分析过程(注意黑色加粗字)分解成一个个小问呈现,助梳理解题思路.
(1)审题得基本信息:①谁在动: ;从哪往哪动: ;③动了多长: .
(2)根据运动过程确定状态图和界点图:①先画出初状态和末状态:初状态为点E 从点B 出发一小段时的位置,末状态为点E 在BC的延长线上(如图1),观察△DEF 运动到△DE F ;根据初末状态确定临界点(此点前后图形状态不同):D是定点,点E 运动到点E 是从点 D 的右侧运动到点D 的左侧,所以点 E 与点D重合时是一个临界点,画出界点图,如图2,这时x= .点F 运动到点F 时,点F 从DE 的上方运动到DE 的下方,所以点 F 落在直线DE 上时是一个临界点,画出界点图,如图3,这时x= ;③根据界点图画出临界点前后的状态图:当点E 在BD 上,点F 在DE 上方时,如图4;当点E 在BD 的延长线上,点F 在DE 上方时,如图5;当点E 在BD 的延长线上,点 F 在DE 下方时,如图6.
(3)面积计算:一般两种方法,①几何图形面积公式:底、高是定长或可以用含x的代数式表示.常用求线段长的方法有:同一直线上和差,把线段放在几何图形中利用全等、相似、勾股定理来求线段长;用面积的和差:当所求几何图形的底和高不容易用含x的代数式表示线段长时,或所求几何图形是不规则几何图形时,可以把所求的几何图形转换成其他几何图形的和差,利用其他几何图形的面积来求.
2.如图,四边形ABCD 是边长为2cm 的正方形,E,F 分别为边AD,CD 的中点,点O为正方形ABCD 的中心,连接OE,OF,点 P 从点 E 出发,沿 E-O-F 运动,同时点Q 从点 B 出发,沿BC 运动,两点运动的速度均为1 cm/s,当点P 运动到点 F 时,两点同时停止运动,连接BP,PQ.设运动时间为 t s,△BPQ 的面积为 下列图象能大致反映 S 与 t 之间的函数关系的是 ( )
3.2024本溪模拟如图,在菱形 ABCD 中, ,点 P,Q 同时从D点A 出发,点 P 以1cm/s的速度沿A-C-D的方向运动,点Q 以2cm/s的速度沿 A-B-C-D的方向运动,当其中一点到达点 D 时,两点同时停止运动.设运动时间为 xs,△APQ 的面积为 y cm ,则下列图象能大致反映y与x之间的函数关系的是 ( )
4.如图,在Rt△ABC中,∠ABC=90°,AB=4,BC=2,BD 是边 AC 上的高.点E,F 分别在边AB,BC上(不与端点重合),且DE⊥DF.设AE=x,四边形DEBF 的面积为y,则y关于x的函数图象为 ( )
考向 2:图形重叠的面积问题
5.如图,在Rt△ABC中,∠ABC=90°,AB=2BC=4,动点 P 从点 A 出发,以每秒1个单位长度的速度沿线段 AB 匀速运动,当点 P 运动到点 B 时,停止运动,过点 P 作 交AC于点Q,将△APQ 沿直线PQ 折叠得到△A'PQ.设动点 P 的运动时间为 ts,△A'PQ与 重叠部分的面积为S,则下列图象能大致反映 S 与t之间的函数关系的是 ( )
6.2023锦州中考如图,在Rt△ABC 中,∠ACB=90°,AC=3,BC=4,在△DEF 中,DE=DF=5,EF=8,BC 与EF 在同一条直线上,点 C 与点 E 重合.△ABC 以每秒1个单位长度的速度沿线段EF 所在直线向右匀速运动,当点 B 运动到点 F 时,△ABC 停止运动.设运动时间为 ts,△ABC 与△DEF 重叠部分的面积为S,则下列图象能大致反映S与t之间的函数关系的是( )
7.2023本溪铁岭辽阳中考如图,在Rt△ABC中,∠ACB=90°,∠A=30°,AB=3cm.动点 P 从点 A出发,以1 cm/s的速度沿射线AB 匀速运动,到点B 停止运动,同时动点Q 从点A 出发,以 的速度沿射线AC 匀速运动.当点 P 停止运动时,点Q 也随之停止运动.在PQ 的右侧以PQ 为边作菱形 PQMN,点 N 在射线 AB 上.设点 P 的运动时间为x s,菱形 PQMN 与△ABC 重叠部分的面积为ycm ,则下列图象能大致反映y 与x之间的函数关系的是 ( )
类型2·函数图象的分析
8.如图1,动点 P 从菱形ABCD 的点A 出发,沿边AB→BC匀速运动,运动到点C时停止.设点 P的运动路程为x,PO的长为y,y与x的函数图象如图2所示,当点 P 运动到BC的中点时,PO的长为 ( )
A.2 B.3 C.
9.2024营口二模如图1,在△ABC 中,∠C=90°,点 D 从点 A 出发,沿A-C-B 运动到点 B 停止,过点 D 作 DE⊥AB,垂足为E,连接BD.设点 D 的运动路径长为x,△BDE 的面积为y,若y与x的对应关系如图2所示,则a-b的值为 ( )
A. B.3 C. D.2
专题 1 几何动态问题中函数图象的判断与分析
1. C思路引导(1)点 E;从点 B 沿射线 BC 动;x (2)4;7
详解∵AB=AC=5,BC=8,AD为中线,
∴AD⊥BC,CD=BD=4.
在 Rt△ABD 中,根据勾股定理,得. 当点E 与点D 重合时,如图1,BE=4.
当点 F 在BC 上时,如图2,由旋转的性质,得 AE=AF,∠EAF=90°.
又AD⊥BC,∴ED=FD.∴AD=ED=FD=3.
∴BE=ED+BD=7.
①当0≤x<4 时,如图3,过点 F 分别作 FH⊥DA 交DA的延长线于点 H,FG⊥BD 于点G.
∴∠H=∠FGE=∠ADE=90°.
∴∠HAF+∠HFA=90°,四边形 HDGF 为矩形.
∴HD=FG.
∵∠FAE=90°,∴∠HAF+∠DAE=90°.
∴∠HFA=∠DAE.
又∠H=∠ADE=90°,AF=AE,∴△HAF≌△DEA.
∴FH=AD=3,HA=DE=BD--BE=4-x.
∴FG=HD=HA+AD=7-x.
故 A,B选项不正确.
当4≤x<7时,如图4,过点 F 作FM⊥AD 于点M.
同理①,得△AMF≌△EDA.
∴AM=ED=x-4,MF=DA=3.
∴MD=AD-AM=3-(x-4)=7-x.
③当x≥7时,如图5,过点 F 作FN⊥AD 交AD 的延长线于点 N.
同理①,得△AED≌△FAN.
∴AD=FN=3,ED=AN=x-4.
∴DN=AN-AD=x-4-3=x-7.
故D选项不正确.故选 C.
2. D 详解根据题意,得四边形 EOFD 为正方形,OE=OF=1.
当0
故 A,C选项不正确.
当1
3. A 详解∵四边形 ABCD 是菱形,
∴AB=BC=CD=AD=2,∠B=∠D=60°.
∴△ABC 和△ACD 都是等边三角形.
∴∠CAB=∠ACB=∠ACD=60°.
如图1,过点 C 作CM⊥AB 于点 M、
∴∠BMC=90°.∴CM=BC· sin 60°=
当0≤x≤1时,如图2,过点 P 作PE⊥AB 于点 E、
∴∠AEP=90°.此时AQ=2x、AP=x、
故D选项不正确.
当1
故 B选项不正确.
当2
此时CP=x-2,CQ=2x-4.∴PQ=x-2.
故 C 选项不正确.故选 A.
4. A 详解如图,过点 D作 DH⊥AB 于点 H.∴∠DHA=90°.
在 Rt△ABC 中,根据勾股定理,得 ∵BD 是边AC上的高,
在 Rt△BCD 中,根据勾股定理,得
∵DE⊥DF,BD⊥AC,∴∠EDF=∠BDC=∠ABC=90°.
∴∠BDE = 90°-∠BDF = ∠CDF,∠DBE = 90°-∠CBD=∠C.
∴△BDE∽△CDF.
∴y随x的增大而减小,且 y与x的函数图象为线段(不含端点).
观察各选项图象可知,A符合题意.故选 A.
5. D 详解∵∠ABC=90°,AB=2BC=4,∴tanA= 由题意,知AP=l.
∵PQ⊥AB,∴∠APQ=90°.∴PQ=AP·tanA=
由折叠的性质,得A'P=AP=t,∠APQ=∠A'PQ=90°.当点 P 与AB 中点重合时,AP+A'P=AB=4.∴t=2.当点 P 在AB 中点的左侧,即0≤t<2时,
△A'PQ与△ABC 重叠部分的面积为
故 A,C选项不正确.
当点 P 在AB 中点的右侧,即2≤t≤4时,如图.
由折叠的性质,得.A'P=AP=t,∠APQ=∠A'PQ=90°,
∴△A'PQ 与△ABC 重叠部分的面积为 故B选项不正确.故选 D.
6. A 详解如图1,过点 D 作DH⊥EF 于点 H.
∴∠DHE=90°.
∵DE=DF=5,EF=8,
在 Rt△DHE 中,根据勾股定理,得
在 Rt△ABC 中,根据勾股定理,得
∵AB=DE=5,BC=EH=4,AC=DH=3,
∴△ABC≌△DEH.∴∠B=∠DEH=∠F.
①当0≤t<4时,如图2,设AC 与DE 相交于点M.
故 B,D选项不正确.
②当4≤t≤8时,如图 3,设 AB 交 DF 于点M,AC 交 DF于点N,过点 M 作MH⊥AC 于点 H.
∵CE=t,∴CF=8-t.
∵∠ACB=90°,∴∠ABC+∠A=∠F+∠CNF=90°.
∵∠ABC=∠F,∴∠A=∠CNF=∠MNH.∴MA=MN.
故C选项不正确.故选 A.
7. A详解∵∠ACB=90°,∠A=30°,AB=3,
如图1,过点 P 作PD⊥AC于点 D,过点 Q 作QE⊥AB 于点E.∴∠ADP=∠PEQ=90°.
由题意,得AP=x,AQ= x.
∴PD 是线段AQ 的垂直平分线.
∴∠PQA=∠A=30°,PQ=AP=x.∴∠QPE=60°.
∵四边形 PQMN 是菱形,
∴PQ=PN=MN=QM=x,PQ∥MN.
∴∠MNB=∠QPE=60°.
当点 M 运动到直线 BC 上时,如图2.
∵四边形 PQMN 是菱形,∴QM∥PN.
∴∠A=∠CQM=30°.
又
解得x=1、
当点 Q 运动到与点C 重合时,如图3、
∵∠A=∠AQP=30°,∴∠PQB=∠PBQ=60°、
∴PQ=PB.∴此时点 N 与点B 重合、
当点 P 运动到与点B 重合时,AP=AB=3.∴x=3.
当0≤x≤1时,
故B选项不正确.
当 时,如图4,过点 F 作 FG⊥AB 于点G,GF 的延长线交 QM 于点 R,设QM 交 BC 于点 S.∴∠FGN=90°.
∵∠FNB=∠CBA=60°,QM∥PN,
∴∠NFB =∠SFM =∠M =∠FSM = 60°,∠FRM =∠FGN=90°.
∴△NFB 和△SFM 均是等边三角形.
∴BN=NF=AB-AP-PN=3-2x.
∴FM=SM=MN-NF=3x-3.
当 时,如图5,设 PQ 交 BC 于点 H,过点 H 作HI⊥AB 于点1、
∴∠HIB=90°.同理可得△PHB 是等边三角形.
∵y=S△PHB,
故选 A.
8. C详解根据图象,得当x=0时,PO=AO=4.
当点 P 运动到点 B 时,PO=BO=2.
∵四边形ABCD 是菱形,∴AB=BC,∠AOB=∠BOC=90°.
在 Rt△AOB 中,根据勾股定理,得
∵P 为BC 的中点, 故选 C.
9. D详解由函数图象的拐点,得AC=3,AC+BC=7.
在 Rt△ABC 中,根据勾股定理,得
当y=a,x=AD=2.5时,点D 在AC上,如图1.
∵DE⊥AB,∴∠DEA=∠BED=90°.
∵∠A=∠A,∠DEA=∠C=90°,∴△ADE∽△ABC.
即
∴DE=2,AE=1.5.∴BE=AB-AE=3.5.
即a=3.5.
当y=b,x=4.5时,点 D 在BC上,如图2.
∵AC+BC=7,AC+CD=4.5,∴BD=2.5.
∵∠B=∠B,∠BED=∠C=90°,∴△BDE∽△BAC.
即
即b=1.5.
∴α-b=3.5-1.5=2.故选 D.
同课章节目录
