2025年中考数学二轮复习几何重难选填题:专题1 几何图形的变换(含答案)
文档属性
| 名称 | 2025年中考数学二轮复习几何重难选填题:专题1 几何图形的变换(含答案) | 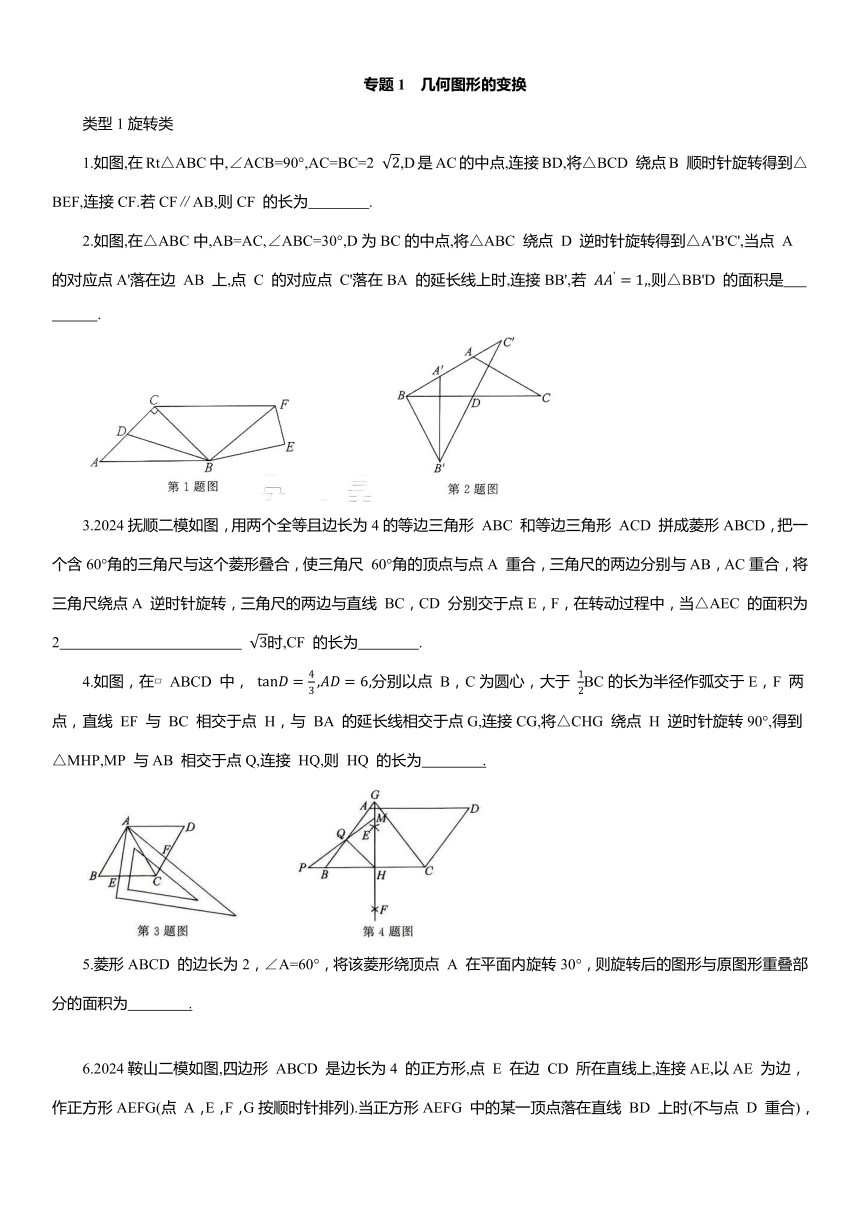 | |
| 格式 | docx | ||
| 文件大小 | 367.7KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 通用版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2025-05-29 13:48:08 | ||
图片预览





文档简介
专题1 几何图形的变换
类型1旋转类
1.如图,在Rt△ABC中,∠ACB=90°,AC=BC=2 ,D是AC的中点,连接BD,将△BCD 绕点B 顺时针旋转得到△BEF,连接CF.若CF∥AB,则CF 的长为 .
2.如图,在△ABC中,AB=AC,∠ABC=30°,D为BC的中点,将△ABC 绕点 D 逆时针旋转得到△A'B'C',当点 A 的对应点A'落在边 AB 上,点 C 的对应点 C'落在BA 的延长线上时,连接BB',若 ,则△BB'D 的面积是 .
3.2024抚顺二模如图,用两个全等且边长为4的等边三角形 ABC 和等边三角形 ACD 拼成菱形ABCD,把一个含60°角的三角尺与这个菱形叠合,使三角尺 60°角的顶点与点A 重合,三角尺的两边分别与AB,AC重合,将三角尺绕点A 逆时针旋转,三角尺的两边与直线 BC,CD 分别交于点E,F,在转动过程中,当△AEC 的面积为2 时,CF 的长为 .
4.如图,在 ABCD 中, 分别以点 B,C为圆心,大于 BC的长为半径作弧交于E,F 两点,直线 EF 与 BC 相交于点 H,与 BA 的延长线相交于点G,连接CG,将△CHG 绕点 H 逆时针旋转90°,得到△MHP,MP 与AB 相交于点Q,连接 HQ,则 HQ 的长为 .
5.菱形ABCD 的边长为2,∠A=60°,将该菱形绕顶点 A 在平面内旋转30°,则旋转后的图形与原图形重叠部分的面积为 .
6.2024鞍山二模如图,四边形 ABCD 是边长为4 的正方形,点 E 在边 CD 所在直线上,连接AE,以AE 为边,作正方形AEFG(点 A,E,F,G按顺时针排列).当正方形AEFG 中的某一顶点落在直线 BD 上时(不与点 D 重合),正方形AEFG 的面积为 .
类型2·翻折类
7.如图,四边形ABCD为矩形,已知AB=5,AD=8,P 是直线AD 上的一个动点,将矩形 ABCD 沿线段 BP 折叠,使得点 A 恰好落在矩形的对角线上,则AP 的长为 .
思路引导 将翻折类题目的解题思路核心点指出,并以此题为例应用分析,助明晰解题思路,
解题思路核心点:分析时抓住“翻折后对应边相等,对应角相等,对应点连线被对称轴垂直平分”,再结合图形中其他条件,解决问题.
(1)审题得基本信息:矩形 ABCD 的对角线为 ;由AB=5,AD=8,得BD=AC= .
(2)①当点A 在对角线BD 上时,如图1.设AP=x、根据翻折后对应边相等,得 再根据翻折后对应角相等,得∠DA P= .利用勾股定理列方程可求得x= ,
②当点A 在对角线AC上时,如图2.根据翻折对应点连线被对称轴垂直平分可得.
【变式——趁热打铁练习透】
7.1 如7题图,四边形ABCD 为矩形,已知AB=5,AD=8,P 是直线AD上的一个动点,将矩形ABCD 沿线段BP 折叠,使得点 A 恰好落在矩形ABCD 平行于AB 的对称轴上,则AP 的长为 .
8.2023本溪铁岭辽阳中考如图,在三角形纸片ABC中,AB=AC,∠B=20°,D 是边 BC 上的动点,将三角形纸片沿AD 对折,使点 B 落在点 B'处,当B'D⊥BC时,∠BAD 的度数为 .
9.如图,在Rt△ABC中,∠ACB=90°,CD 是AB 边上的中线,将△ACD 沿CD 折叠,当点A 落在点 A'处时,恰好CA'⊥AB,若BC=2,则CA'的长为 .
10.如图,在矩形ABCD 中,AB=3,AD=5,点 E 在 DC 上,将矩形 ABCD 沿AE 折叠,点 D 恰好落在 BC 边上的点 F 处,则 tan∠EFC= .
11.2024辽宁模拟如图,正方形纸片ABCD 的边长为5,E 是边 BC 的中点,连接AE,沿 AE 折叠该纸片,使点 B 落在点 F 处,则CF 的长为 .
12.2024沈阳零模如图,将菱形纸片ABCD 沿过点 C 的直线折叠,使点 D 落在射线 CA 上的点 E处,折痕CP 交 AD 于点 P.若 ,则 CA 的长为 .
13.如图,在△ABC中,∠C=90°,AC=2,BC=4,D为AB 的中点,点 E 在 BC 边上,连接 DE,AE,将△BDE 沿 DE 折叠得到△FDE,连接AF,若以点 D,E,F,A 为顶点的四边形为平行四边形,则CE 的长为 .
14.2024铁岭二模如图,在矩形 ABCD 中,AD=5,AB=7,E 为 DC 上一动点,将 沿 AE折叠,当点 D 的对应点 D'落在∠ABC 的平分线上时,DE 的长为 .
15.如图,在正方形纸片ABCD 中,E 是AB 边的中点,将正方形纸片沿EC 折叠,点 B 落在点 P处,延长CP 交AD 于点Q,连接AP 并延长交CD 于点 F.给出以下结论:①△AEP 为等腰三角形;②F 是CD的中点;③AP : PF=2:3;④cos∠DCQ= 其中正确的是 .(填序号)
专题1 几何图形的变换
详解如图,过点 B 作 BG⊥CF 于点G.
∴∠BGC=∠BGF=90°.
∵∠ACB=90°,AC=BC=2 ,D 是AC的中点,
∴CD= ,∠ABC=45°.
根据勾股定理,得 由旋转的性质可知,△DCB≌△FEB.
∵CF∥AB,∴∠ABC=∠BCG=45°.
∴∠CBG=90°-∠BCG=45°=∠BCG.∴BG=CG.
在 Rt△BCG 中,
根据勾股定理,得
∴CF=CG+GF=2+
详解如图,设A'B'与BD 交于点O,连接A'D,AD.
∵D 为BC 的中点,AB=AC,∠ABC=30°,
∴AD⊥BC,AD 是∠BAC 的平分线,∠ABC=∠C=30°.
∴∠ADB=∠ADC=90°,∠BAC=120°.∴∠BAD=60°.由旋转的性质,得A'D=AD,∠B'A'C'=∠BAC=120°,∠A'DB'=∠ADB=90°.
∴△A'AD 是等边三角形.
∴A'A=AD=A'D=1,∠ADA'=60°.
∴∠A'DO=30°,∠B'DO=60°.
∵∠BA'B'=180°-∠B'A'C'=60°,∴∠BA'B'=∠A'AD.
∴A'B'∥AD.∴∠A'OD=∠ADC=90°.
在 Rt△A'OD 中,根据勾股定理,得
∵∠A'DB'=90°,∠OB'D=90°-∠B'DO=30°,
∴A'B'=2A'D=2.
∵∠A'BD=∠A'DO,A'O=A'O,∠A'OB=∠A'OD,
∴△A'OB≌△A'OD.∴OB=OD.∴BD=2OD=
3.6或2 详解如图1,当点E 在线段BC 上,点 F 在线段CD上时,∵△ABC 和△ACD 是等边三角形,
∴∠B=∠ACF=∠BAC=60°,AB=AC.
又∠EAF=60°,∴∠BAE+∠EAC=∠CAF+∠EAC=60°.
∴∠BAE=∠CAF.
又AB=AC,∠B=∠ACF,∴△ABE≌△ACF.∴BE=CF.
过点 A 作AH⊥BC 于点 H.∴∠AHB=90°.
∵sin B=AH,∠B=60°,AB=4,∴AH=AB·sín 60°=2
∵△AEC 的面积是
∴CE=2.∴CF=BE=BC--CE=4-2=2.
如图2,当点E 在BC 的延长线上,点F 在CD 的延长线上时,同理可得△ABE≌△ACF,CE=2.
∴CF=BE=BC+CE=4+2=6.
∴CF 的长为6或2.
详解如图,过点 Q 作QF⊥BH 于点 F.
∴∠BFQ=∠HFQ=90°.
∵四边形ABCD 是平行四边形,
∴∠ABC=∠D,AD=BC=6.∴tan D=tan∠ABC= 由题意,得GF 垂直平分BC.
∴BG=CG,BH=CH=3,∠BHG=90°.
由旋转的性质,得
CH=MH=3,GH=PH=4,∠GCH=∠PMH.
∴∠PMH=∠GBC.∴∠GMQ=∠PBQ.
又∠GQM=∠PQB,GM=PB=PH-BH=4-3=1,
∴△GQM≌△PQB.∴MQ=BQ.
又MH=BH,HQ=HQ,∴△MHQ≌△BHQ.
即QF=HF.
设BF=3x,则(QF=4x,HF=3-3x.
∴4x=3-3x.解得
详解 ①将该菱形绕顶点 A 在平面内顺时针旋转30°.如图,连接AC,BD 相交于点O,设BC 交C'D'于点E.
∵四边形ABCD 是菱形,∠DAB=60°,
∴∠CAB=∠CAD=30°,AC⊥BD,AO=CO,BO=DO,AB=AD=BC=2.
∴∠AOD=90°,∠CAB=∠ACB=30°,△ABD 是等边三角形.∴BD=2.
∵菱形 ABCD 绕点 A 顺时针旋转30°得到菱形 AB'C'D',
∴A,D',C 三点共线,
∵重叠部分的面积:
∴重叠部分的面积
②将该菱形绕顶点 A 在平面内逆时针旋转30°,同①方法可得重叠部分的面积为
综上所述,重叠部分的面积为
6.20或80详解当点 F 在直线 BD 上时,如图1,过点 F 作FM⊥CD,交CD的延长线于点M.∴∠M=90°.
∵四边形ABCD 是正方形,∴∠BDC=45°,∠ADE=90°.
∴∠FDM=∠BDC=45°,∠AED+∠EAD=90°.
∴△DFM 是等腰直角三角形.∴DM=FM.
∵四边形AEFG 是正方形,∴EF=AE,∠AEF=90°.
∴∠AED+∠FEM=90°.∴∠EAD=∠FEM.
又∠ADE=∠M,AE=EF,∴△AED≌△EFM.
∴DE=MF,AD=EM.∴DE=DM=MF.
∵DE+DM=EM,∴2DE=AD=4.∴DE=2.
在 Rt△ADE中,根据勾股定理,得
∴正方形AEFG 的面积为20.
当点G 在直线 BD 上时,如图2,过点 G 作GN⊥AD,交AD 的延长线于点N,此时点 E 在DC 的延长线上.
同理可得△AED≌△GAN,△DGN 是等腰直角三角形.
∴AD=GN=4,DN=GN.
∴DN=4.∴AN=AD+DN=8.
在 Rt△AGN 中,根据勾股定理,得
∴正方形AEFG 的面积为80.
综上所述,正方形AEFG 的面积为20或80.
或
思路引导(1)AC,BD;
详解①当点A 在对角线 BD 上时,如图1、
∵四边形ABCD 是矩形、∴∠BAD=∠ABC=90°.
根据勾股定理、得 设AP=x,则 PD=8-x、
∵翻折后对应边相等、∴A B=AB=5,A P=AP=x.
∵翻折后对应角相等、∴∠PA B=∠A=90°.
∴∠DA P=90°.
在 Rt△DA P中、根据勾股定理,
解得
②当点 A 在对角线AC 上时,如图2.
∵翻折对应点连线被对称轴垂直平分,
∴AA 被 PB 垂直平分.
综上所述,AP 的长为 或
7.1. 或10 详解设矩形 ABCD 平行于 AB 的对称轴为GH,点 G 在AD 上,点 H 在BC 上.
如图1,点 A 恰好落在GH 上的点A'处.
∵四边形 ABCD 是矩形,
∴∠A=∠ABC=90°,AD=BC=8.
∵GH 是矩形ABCD 的对称轴,
∴四边形GABH 是矩形.∴GH=AB=5.
根据折叠的性质,得
根据勾股定理,得
在 Rt△A'GP 中,根据勾股定理;
解得
如图2,点A 恰好落在GH 上的点A"处,设 PB 交GH 于点 E,连接AE.
∵四边形 ABCD 是矩形,
∴∠DAB=∠ABC=90°,AD=BC=8.
∵GH 是矩形ABCD 的对称轴,
∴AG= AD=4,GH∥AB.∴∠ABP=∠A″EB.
根据折叠的性质,得AB=A"B=5,∠ABP=∠A"BE,
∴四边形 ABA"E 是平行四边形.
在 Rt△AGE 中,根据勾股定理,得
∵GH∥AB,∴△PGE∽△PAB.
即
∴GP=6.∴AP=AG+GP=10.
综上所述,AP 的长为 或10.
8.25°或115°详解根据折叠的性质,得
∵B'D⊥BC,∴∠BDB'=90°.
①当点 B'在 BC 下方时,如图1.
∴∠BAD=180°-∠B-∠ADB=180°-20°-135°=25°.
②当点 B'在BC 上方时,如图2.
综上所述,∠BAD 的度数为25°或 115°.
9.2 详解∵∠ACB=90°,CD 是AB 边上的中线,∴CD=AD.∴∠ACD=∠A.
根据翻折的性质,得
∴∠ACD=∠A'CD=∠A.
如图,设CA'交AB 于点 E.
∵CA'⊥AB,∴∠CEA=90°.
∵∠CEA+∠ACD+∠A'CD+∠A=180°,∴∠A=30°.
10. 详解∵四边形 ABCD 为矩形、
∴BC=AD=5,CD=AB=3,∠B=∠C=90°.
根据折叠的性质、得.AF=AD=5、EF=DE.
根据勾股定理,得
∴CF=BC-BF=1.
设CE=x,则 EF=DE=3-x.
根据勾股定理.
解得
11. 详解如图,连接BF 交AE 于点G.
根据折叠的性质,得△ABE≌△AFE,AE 垂直平分BF.
∴BE=EF,∠BEA=∠FEA,∠BGE=90°,BG=FG.
∵四边形ABCD 是正方形,∴∠ABC=90°,AB=BC=5.
∵E 是边BC 的中点,
∴∠EFC=∠ECF.
根据勾股定理,得
∵∠BEF=∠BEA+∠FEA=∠EFC+∠ECF,
∴∠BEA=∠ECF.∴AE∥FC.
∴∠BGE=∠BFC=90°.
根据勾股定理,得
详解如图,过点 A 作AF⊥PE 于点 F.
∴∠AFP=∠AFE=90°.
∵四边形ABCD 是菱形,∴∠D=∠B=30°,AD=CD.
根据折叠的性质,得∠E=∠D=30°,CD=CE,PD=PE.
∴∠FAP=45°=∠APF.∴PF=AF=AP·cos45°=1.
∴EF= AF = ,AE=2.∴PD=PE=PF+EF=1+
13.1 或4- 详解当点 F 在AD 下方时,如图1.
根据勾股定理,得
∵D为AB 的中点,∴
∵四边形ADEF 是平行四边形,.
根据折叠的性质,得
∴CE=BC-BE=4-
当点 F 在AD上方时,如图2.
同理可得
根据勾股定理,得
综上所述,CE 的长为1或
14. 或 详解如图,连接 BD',过点 D'作 MN⊥AB,交AB 于点M,交CD 于点 N.
∴∠D'MA=∠D'MB=90°.∴∠D'AM+∠AD'M=90°.
∵四边形ABCD 是矩形,
∴∠D=∠ABC=90°,AB∥CD.
∴四边形 DAMN 是矩形.∴AD=MN=5.
∵点 D 的对应点 D'落在∠ABC 的平分线上,
设D'M=MB=x,则AM=7-x、
根据折叠的性质、得 AD= AD'=5,DE= D'E,∠D=
∴∠ED'N+∠AD'M=90°.∴∠ED'N=∠D'AM.
∵∠END'=∠D'MA,∴△END'∽△D'MA.
在 Rt△AMD'中,根据勾股定理,
解得
当D'M=MB=3时,
当D'M=MB=4时,
综上所述,DE 的长为 或
15.①②③详解如图,连接 EQ,BP,设 BP 交EC 于点G.
∵E为AB 的中点,∴AE=EB.
设正方形的边长为2a,则AE=EB=a.
根据折叠的性质,得∠1=∠2,BP⊥EC,EP=EB=a.
∴EA=EP.∴△AEP 是等腰三角形.故①正确.二
设∠1=∠2=α.∴∠AEP=180°-2α.
∵EA=EP,∴∠3=∠4=α.
∴∠2=∠3.∴AF∥EC.
∵四边形ABCD 是正方形,∴∠D=90°,AE∥FC.
∴四边形AECF 是平行四边形.∴CF=AE=a.
∴CF=FD=a,即 F 是CD的中点.故②正确.
∵BP⊥EC,AF∥EC,∴∠BPF=∠BGC=90°.
在 Rt△ADF 中,根据勾股定理,得
设AP=x,则 BP=2x.根据勾股定理,得
即
∴AP:PF=2:3.故③正确.
∵四边形ABCD 是正方形,∴∠QAE=∠EBC=90°.
根据折叠的性质,得∠EBC=∠EPC=90°,EB=EP.
∴∠EPQ=90°=∠EAQ,EA=EB=EP.
又EQ=EQ,∴Rt△AEQ≌Rt△PEQ.∴AQ=PQ.
又EA=EP,∴EQ⊥AP,∴∠AEQ+∠4=90°.
又∠AQE+∠AEQ=90°,∴∠AQE=∠4=α.
在 Rt△QDC 中,根据勾股定理,得
故④不正确.
综上所述,正确的结论为①②③.
类型1旋转类
1.如图,在Rt△ABC中,∠ACB=90°,AC=BC=2 ,D是AC的中点,连接BD,将△BCD 绕点B 顺时针旋转得到△BEF,连接CF.若CF∥AB,则CF 的长为 .
2.如图,在△ABC中,AB=AC,∠ABC=30°,D为BC的中点,将△ABC 绕点 D 逆时针旋转得到△A'B'C',当点 A 的对应点A'落在边 AB 上,点 C 的对应点 C'落在BA 的延长线上时,连接BB',若 ,则△BB'D 的面积是 .
3.2024抚顺二模如图,用两个全等且边长为4的等边三角形 ABC 和等边三角形 ACD 拼成菱形ABCD,把一个含60°角的三角尺与这个菱形叠合,使三角尺 60°角的顶点与点A 重合,三角尺的两边分别与AB,AC重合,将三角尺绕点A 逆时针旋转,三角尺的两边与直线 BC,CD 分别交于点E,F,在转动过程中,当△AEC 的面积为2 时,CF 的长为 .
4.如图,在 ABCD 中, 分别以点 B,C为圆心,大于 BC的长为半径作弧交于E,F 两点,直线 EF 与 BC 相交于点 H,与 BA 的延长线相交于点G,连接CG,将△CHG 绕点 H 逆时针旋转90°,得到△MHP,MP 与AB 相交于点Q,连接 HQ,则 HQ 的长为 .
5.菱形ABCD 的边长为2,∠A=60°,将该菱形绕顶点 A 在平面内旋转30°,则旋转后的图形与原图形重叠部分的面积为 .
6.2024鞍山二模如图,四边形 ABCD 是边长为4 的正方形,点 E 在边 CD 所在直线上,连接AE,以AE 为边,作正方形AEFG(点 A,E,F,G按顺时针排列).当正方形AEFG 中的某一顶点落在直线 BD 上时(不与点 D 重合),正方形AEFG 的面积为 .
类型2·翻折类
7.如图,四边形ABCD为矩形,已知AB=5,AD=8,P 是直线AD 上的一个动点,将矩形 ABCD 沿线段 BP 折叠,使得点 A 恰好落在矩形的对角线上,则AP 的长为 .
思路引导 将翻折类题目的解题思路核心点指出,并以此题为例应用分析,助明晰解题思路,
解题思路核心点:分析时抓住“翻折后对应边相等,对应角相等,对应点连线被对称轴垂直平分”,再结合图形中其他条件,解决问题.
(1)审题得基本信息:矩形 ABCD 的对角线为 ;由AB=5,AD=8,得BD=AC= .
(2)①当点A 在对角线BD 上时,如图1.设AP=x、根据翻折后对应边相等,得 再根据翻折后对应角相等,得∠DA P= .利用勾股定理列方程可求得x= ,
②当点A 在对角线AC上时,如图2.根据翻折对应点连线被对称轴垂直平分可得.
【变式——趁热打铁练习透】
7.1 如7题图,四边形ABCD 为矩形,已知AB=5,AD=8,P 是直线AD上的一个动点,将矩形ABCD 沿线段BP 折叠,使得点 A 恰好落在矩形ABCD 平行于AB 的对称轴上,则AP 的长为 .
8.2023本溪铁岭辽阳中考如图,在三角形纸片ABC中,AB=AC,∠B=20°,D 是边 BC 上的动点,将三角形纸片沿AD 对折,使点 B 落在点 B'处,当B'D⊥BC时,∠BAD 的度数为 .
9.如图,在Rt△ABC中,∠ACB=90°,CD 是AB 边上的中线,将△ACD 沿CD 折叠,当点A 落在点 A'处时,恰好CA'⊥AB,若BC=2,则CA'的长为 .
10.如图,在矩形ABCD 中,AB=3,AD=5,点 E 在 DC 上,将矩形 ABCD 沿AE 折叠,点 D 恰好落在 BC 边上的点 F 处,则 tan∠EFC= .
11.2024辽宁模拟如图,正方形纸片ABCD 的边长为5,E 是边 BC 的中点,连接AE,沿 AE 折叠该纸片,使点 B 落在点 F 处,则CF 的长为 .
12.2024沈阳零模如图,将菱形纸片ABCD 沿过点 C 的直线折叠,使点 D 落在射线 CA 上的点 E处,折痕CP 交 AD 于点 P.若 ,则 CA 的长为 .
13.如图,在△ABC中,∠C=90°,AC=2,BC=4,D为AB 的中点,点 E 在 BC 边上,连接 DE,AE,将△BDE 沿 DE 折叠得到△FDE,连接AF,若以点 D,E,F,A 为顶点的四边形为平行四边形,则CE 的长为 .
14.2024铁岭二模如图,在矩形 ABCD 中,AD=5,AB=7,E 为 DC 上一动点,将 沿 AE折叠,当点 D 的对应点 D'落在∠ABC 的平分线上时,DE 的长为 .
15.如图,在正方形纸片ABCD 中,E 是AB 边的中点,将正方形纸片沿EC 折叠,点 B 落在点 P处,延长CP 交AD 于点Q,连接AP 并延长交CD 于点 F.给出以下结论:①△AEP 为等腰三角形;②F 是CD的中点;③AP : PF=2:3;④cos∠DCQ= 其中正确的是 .(填序号)
专题1 几何图形的变换
详解如图,过点 B 作 BG⊥CF 于点G.
∴∠BGC=∠BGF=90°.
∵∠ACB=90°,AC=BC=2 ,D 是AC的中点,
∴CD= ,∠ABC=45°.
根据勾股定理,得 由旋转的性质可知,△DCB≌△FEB.
∵CF∥AB,∴∠ABC=∠BCG=45°.
∴∠CBG=90°-∠BCG=45°=∠BCG.∴BG=CG.
在 Rt△BCG 中,
根据勾股定理,得
∴CF=CG+GF=2+
详解如图,设A'B'与BD 交于点O,连接A'D,AD.
∵D 为BC 的中点,AB=AC,∠ABC=30°,
∴AD⊥BC,AD 是∠BAC 的平分线,∠ABC=∠C=30°.
∴∠ADB=∠ADC=90°,∠BAC=120°.∴∠BAD=60°.由旋转的性质,得A'D=AD,∠B'A'C'=∠BAC=120°,∠A'DB'=∠ADB=90°.
∴△A'AD 是等边三角形.
∴A'A=AD=A'D=1,∠ADA'=60°.
∴∠A'DO=30°,∠B'DO=60°.
∵∠BA'B'=180°-∠B'A'C'=60°,∴∠BA'B'=∠A'AD.
∴A'B'∥AD.∴∠A'OD=∠ADC=90°.
在 Rt△A'OD 中,根据勾股定理,得
∵∠A'DB'=90°,∠OB'D=90°-∠B'DO=30°,
∴A'B'=2A'D=2.
∵∠A'BD=∠A'DO,A'O=A'O,∠A'OB=∠A'OD,
∴△A'OB≌△A'OD.∴OB=OD.∴BD=2OD=
3.6或2 详解如图1,当点E 在线段BC 上,点 F 在线段CD上时,∵△ABC 和△ACD 是等边三角形,
∴∠B=∠ACF=∠BAC=60°,AB=AC.
又∠EAF=60°,∴∠BAE+∠EAC=∠CAF+∠EAC=60°.
∴∠BAE=∠CAF.
又AB=AC,∠B=∠ACF,∴△ABE≌△ACF.∴BE=CF.
过点 A 作AH⊥BC 于点 H.∴∠AHB=90°.
∵sin B=AH,∠B=60°,AB=4,∴AH=AB·sín 60°=2
∵△AEC 的面积是
∴CE=2.∴CF=BE=BC--CE=4-2=2.
如图2,当点E 在BC 的延长线上,点F 在CD 的延长线上时,同理可得△ABE≌△ACF,CE=2.
∴CF=BE=BC+CE=4+2=6.
∴CF 的长为6或2.
详解如图,过点 Q 作QF⊥BH 于点 F.
∴∠BFQ=∠HFQ=90°.
∵四边形ABCD 是平行四边形,
∴∠ABC=∠D,AD=BC=6.∴tan D=tan∠ABC= 由题意,得GF 垂直平分BC.
∴BG=CG,BH=CH=3,∠BHG=90°.
由旋转的性质,得
CH=MH=3,GH=PH=4,∠GCH=∠PMH.
∴∠PMH=∠GBC.∴∠GMQ=∠PBQ.
又∠GQM=∠PQB,GM=PB=PH-BH=4-3=1,
∴△GQM≌△PQB.∴MQ=BQ.
又MH=BH,HQ=HQ,∴△MHQ≌△BHQ.
即QF=HF.
设BF=3x,则(QF=4x,HF=3-3x.
∴4x=3-3x.解得
详解 ①将该菱形绕顶点 A 在平面内顺时针旋转30°.如图,连接AC,BD 相交于点O,设BC 交C'D'于点E.
∵四边形ABCD 是菱形,∠DAB=60°,
∴∠CAB=∠CAD=30°,AC⊥BD,AO=CO,BO=DO,AB=AD=BC=2.
∴∠AOD=90°,∠CAB=∠ACB=30°,△ABD 是等边三角形.∴BD=2.
∵菱形 ABCD 绕点 A 顺时针旋转30°得到菱形 AB'C'D',
∴A,D',C 三点共线,
∵重叠部分的面积:
∴重叠部分的面积
②将该菱形绕顶点 A 在平面内逆时针旋转30°,同①方法可得重叠部分的面积为
综上所述,重叠部分的面积为
6.20或80详解当点 F 在直线 BD 上时,如图1,过点 F 作FM⊥CD,交CD的延长线于点M.∴∠M=90°.
∵四边形ABCD 是正方形,∴∠BDC=45°,∠ADE=90°.
∴∠FDM=∠BDC=45°,∠AED+∠EAD=90°.
∴△DFM 是等腰直角三角形.∴DM=FM.
∵四边形AEFG 是正方形,∴EF=AE,∠AEF=90°.
∴∠AED+∠FEM=90°.∴∠EAD=∠FEM.
又∠ADE=∠M,AE=EF,∴△AED≌△EFM.
∴DE=MF,AD=EM.∴DE=DM=MF.
∵DE+DM=EM,∴2DE=AD=4.∴DE=2.
在 Rt△ADE中,根据勾股定理,得
∴正方形AEFG 的面积为20.
当点G 在直线 BD 上时,如图2,过点 G 作GN⊥AD,交AD 的延长线于点N,此时点 E 在DC 的延长线上.
同理可得△AED≌△GAN,△DGN 是等腰直角三角形.
∴AD=GN=4,DN=GN.
∴DN=4.∴AN=AD+DN=8.
在 Rt△AGN 中,根据勾股定理,得
∴正方形AEFG 的面积为80.
综上所述,正方形AEFG 的面积为20或80.
或
思路引导(1)AC,BD;
详解①当点A 在对角线 BD 上时,如图1、
∵四边形ABCD 是矩形、∴∠BAD=∠ABC=90°.
根据勾股定理、得 设AP=x,则 PD=8-x、
∵翻折后对应边相等、∴A B=AB=5,A P=AP=x.
∵翻折后对应角相等、∴∠PA B=∠A=90°.
∴∠DA P=90°.
在 Rt△DA P中、根据勾股定理,
解得
②当点 A 在对角线AC 上时,如图2.
∵翻折对应点连线被对称轴垂直平分,
∴AA 被 PB 垂直平分.
综上所述,AP 的长为 或
7.1. 或10 详解设矩形 ABCD 平行于 AB 的对称轴为GH,点 G 在AD 上,点 H 在BC 上.
如图1,点 A 恰好落在GH 上的点A'处.
∵四边形 ABCD 是矩形,
∴∠A=∠ABC=90°,AD=BC=8.
∵GH 是矩形ABCD 的对称轴,
∴四边形GABH 是矩形.∴GH=AB=5.
根据折叠的性质,得
根据勾股定理,得
在 Rt△A'GP 中,根据勾股定理;
解得
如图2,点A 恰好落在GH 上的点A"处,设 PB 交GH 于点 E,连接AE.
∵四边形 ABCD 是矩形,
∴∠DAB=∠ABC=90°,AD=BC=8.
∵GH 是矩形ABCD 的对称轴,
∴AG= AD=4,GH∥AB.∴∠ABP=∠A″EB.
根据折叠的性质,得AB=A"B=5,∠ABP=∠A"BE,
∴四边形 ABA"E 是平行四边形.
在 Rt△AGE 中,根据勾股定理,得
∵GH∥AB,∴△PGE∽△PAB.
即
∴GP=6.∴AP=AG+GP=10.
综上所述,AP 的长为 或10.
8.25°或115°详解根据折叠的性质,得
∵B'D⊥BC,∴∠BDB'=90°.
①当点 B'在 BC 下方时,如图1.
∴∠BAD=180°-∠B-∠ADB=180°-20°-135°=25°.
②当点 B'在BC 上方时,如图2.
综上所述,∠BAD 的度数为25°或 115°.
9.2 详解∵∠ACB=90°,CD 是AB 边上的中线,∴CD=AD.∴∠ACD=∠A.
根据翻折的性质,得
∴∠ACD=∠A'CD=∠A.
如图,设CA'交AB 于点 E.
∵CA'⊥AB,∴∠CEA=90°.
∵∠CEA+∠ACD+∠A'CD+∠A=180°,∴∠A=30°.
10. 详解∵四边形 ABCD 为矩形、
∴BC=AD=5,CD=AB=3,∠B=∠C=90°.
根据折叠的性质、得.AF=AD=5、EF=DE.
根据勾股定理,得
∴CF=BC-BF=1.
设CE=x,则 EF=DE=3-x.
根据勾股定理.
解得
11. 详解如图,连接BF 交AE 于点G.
根据折叠的性质,得△ABE≌△AFE,AE 垂直平分BF.
∴BE=EF,∠BEA=∠FEA,∠BGE=90°,BG=FG.
∵四边形ABCD 是正方形,∴∠ABC=90°,AB=BC=5.
∵E 是边BC 的中点,
∴∠EFC=∠ECF.
根据勾股定理,得
∵∠BEF=∠BEA+∠FEA=∠EFC+∠ECF,
∴∠BEA=∠ECF.∴AE∥FC.
∴∠BGE=∠BFC=90°.
根据勾股定理,得
详解如图,过点 A 作AF⊥PE 于点 F.
∴∠AFP=∠AFE=90°.
∵四边形ABCD 是菱形,∴∠D=∠B=30°,AD=CD.
根据折叠的性质,得∠E=∠D=30°,CD=CE,PD=PE.
∴∠FAP=45°=∠APF.∴PF=AF=AP·cos45°=1.
∴EF= AF = ,AE=2.∴PD=PE=PF+EF=1+
13.1 或4- 详解当点 F 在AD 下方时,如图1.
根据勾股定理,得
∵D为AB 的中点,∴
∵四边形ADEF 是平行四边形,.
根据折叠的性质,得
∴CE=BC-BE=4-
当点 F 在AD上方时,如图2.
同理可得
根据勾股定理,得
综上所述,CE 的长为1或
14. 或 详解如图,连接 BD',过点 D'作 MN⊥AB,交AB 于点M,交CD 于点 N.
∴∠D'MA=∠D'MB=90°.∴∠D'AM+∠AD'M=90°.
∵四边形ABCD 是矩形,
∴∠D=∠ABC=90°,AB∥CD.
∴四边形 DAMN 是矩形.∴AD=MN=5.
∵点 D 的对应点 D'落在∠ABC 的平分线上,
设D'M=MB=x,则AM=7-x、
根据折叠的性质、得 AD= AD'=5,DE= D'E,∠D=
∴∠ED'N+∠AD'M=90°.∴∠ED'N=∠D'AM.
∵∠END'=∠D'MA,∴△END'∽△D'MA.
在 Rt△AMD'中,根据勾股定理,
解得
当D'M=MB=3时,
当D'M=MB=4时,
综上所述,DE 的长为 或
15.①②③详解如图,连接 EQ,BP,设 BP 交EC 于点G.
∵E为AB 的中点,∴AE=EB.
设正方形的边长为2a,则AE=EB=a.
根据折叠的性质,得∠1=∠2,BP⊥EC,EP=EB=a.
∴EA=EP.∴△AEP 是等腰三角形.故①正确.二
设∠1=∠2=α.∴∠AEP=180°-2α.
∵EA=EP,∴∠3=∠4=α.
∴∠2=∠3.∴AF∥EC.
∵四边形ABCD 是正方形,∴∠D=90°,AE∥FC.
∴四边形AECF 是平行四边形.∴CF=AE=a.
∴CF=FD=a,即 F 是CD的中点.故②正确.
∵BP⊥EC,AF∥EC,∴∠BPF=∠BGC=90°.
在 Rt△ADF 中,根据勾股定理,得
设AP=x,则 BP=2x.根据勾股定理,得
即
∴AP:PF=2:3.故③正确.
∵四边形ABCD 是正方形,∴∠QAE=∠EBC=90°.
根据折叠的性质,得∠EBC=∠EPC=90°,EB=EP.
∴∠EPQ=90°=∠EAQ,EA=EB=EP.
又EQ=EQ,∴Rt△AEQ≌Rt△PEQ.∴AQ=PQ.
又EA=EP,∴EQ⊥AP,∴∠AEQ+∠4=90°.
又∠AQE+∠AEQ=90°,∴∠AQE=∠4=α.
在 Rt△QDC 中,根据勾股定理,得
故④不正确.
综上所述,正确的结论为①②③.
同课章节目录
