2025年中考数学二轮复习专题5 二次函数综合(含答案)
文档属性
| 名称 | 2025年中考数学二轮复习专题5 二次函数综合(含答案) |  | |
| 格式 | docx | ||
| 文件大小 | 292.9KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 通用版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2025-05-29 13:48:54 | ||
图片预览




文档简介
专题5 二次函数综合
1.新考向·新定义定义:在平面直角坐标系中,若函数R 的图象经过Rt△ABC 的两个顶点,则称函数R 是 Rt△ABC 的“勾股函数”,函数 R 经过直角三角形的两个顶点的坐标分别为(x ,y ),(x ,y ),且 ,当自变量x 满足 时,函数R 的最大值记为 ymax,最小值记为ymin,令 则 h 是 Rt△ABC 的“DX”值.
已知:在平面直角坐标系中,△ABC是直角三角形,∠ACB=90°,BC∥y轴.
(1)如图,若点 C 的坐标为(1,1),AC=BC=4.
①一次函数、 是 Rt△ABC 的“勾股函数”吗 若是,请说明理由,并求出 Rt△ABC 的“DX”值;若不是,请说明理由;
是否存在反比例函数 是 Rt△ABC的“勾股函数” 若存在,求出k 的值;若不存在,请说明理由.
(2)已知点 A 的坐标为(2,2),点 B 的坐标为(1,m),二次函数 是 Rt△ABC 的“勾股函数”,其中∠ACB=90°.
①若二次函数 经过A,C 两点,则 Rt△ABC 的“DX”值h= ;
若二次函数 经过A,B 两点,且与 Rt△ABC 的边有第三个交点,求m 的取值范围;
③若二次函数 经过A,B 两点,且 Rt△ABC 的“DX”值 求m 的值.
2.如图1,在矩形ABCD 中,已知. ,E 是 AD 的中点,动点 P 从点 A 出发,以每秒1个单位长度的速度沿AD 向点 D 运动,同时动点Q 从点B 出发,以每秒2个单位长度的速度沿折线 BC-CD 运动,当其中一个点到达点 D 时,另一个点也随之停止运动,连接PQ,EQ,设动点 P 运动的时间为t s, 的面积为S,图2是S 关于t的函数关系图象.
(1)填空:
(2)求S 关于t的函数解析式,并写出自变量t 的取值范围;
(3)当点 Q 在线段CD 上运动且S 取最大值时,判断线段 EQ 与对角线AC 的关系,并说明理由;
(4)在整个运动过程中,存在某3个时刻 使得 S 的值相等.
①求 的值;
当 时,求S 的值.
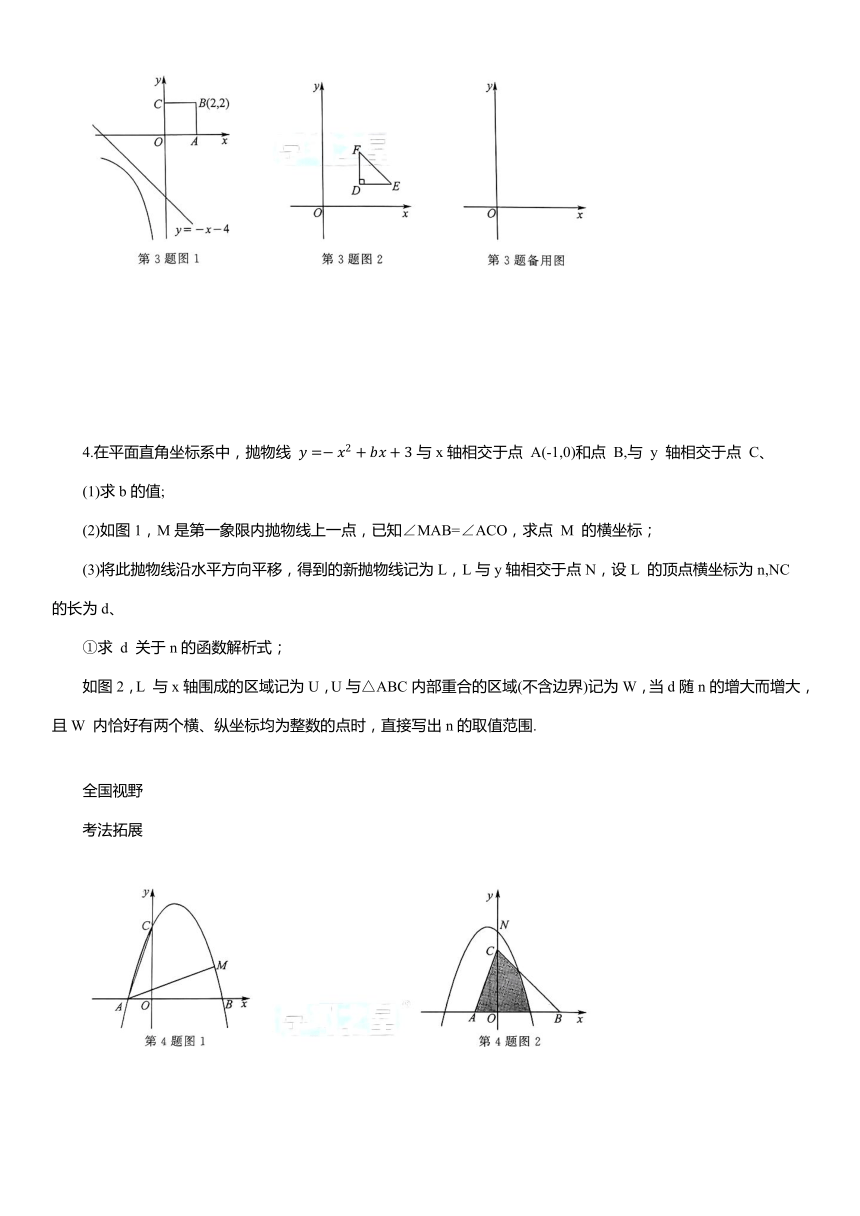
3.中国象棋棋盘上双方的分界处称为“楚河汉界”,以“楚河汉界”比喻两军对垒的分界线,数学中为了对两个图形进行分界,在平面直角坐标系中,对“楚河汉界线”给出如下定义: 是图形G 上的任意一点, 是图形 上的任意一点,若直线l:y=kx+b(k≠0)满足 且 则称直线 是图形 与图形 的“楚河汉界线”.例如:如图1,直线l:y=--x-4是函数 的图象与正方形 OABC 的一条“楚河汉界线”.
(1)在①y=-2x;y=4x-1;③y=-2x+3;④y=-3x-1中,是图1中函数 的图象与正方形 OABC 的“楚河汉界线”的有 ;(填序号)
(2)如图2,在第一象限内,等腰 的两腰分别与坐标轴平行,直角顶点 D 的坐标为 ,若△EDF 与⊙O 的“楚河汉界线”有且只有一条,求此“楚河汉界线”的解析式;
(3)正方形 的一边在y轴上,其他三边都在y轴的右侧,点M(2,t)是此正方形的中心,若存在直线 y=-2x+b是函数 的图象与正方形 的“楚河汉界线”,求t 的取值范围.
4.在平面直角坐标系中,抛物线 与x轴相交于点 A(-1,0)和点 B,与 y 轴相交于点 C、
(1)求b的值;
(2)如图1,M是第一象限内抛物线上一点,已知∠MAB=∠ACO,求点 M 的横坐标;
(3)将此抛物线沿水平方向平移,得到的新抛物线记为L,L与y轴相交于点N,设L 的顶点横坐标为n,NC 的长为d、
①求 d 关于n的函数解析式;
如图2,L 与x轴围成的区域记为U,U与△ABC内部重合的区域(不含边界)记为W,当d随n的增大而增大,且W 内恰好有两个横、纵坐标均为整数的点时,直接写出n的取值范围.
全国视野
考法拓展
5.新新考向·新定义若函数y经过矩形一条对角线上的两个端点,则称函数y 为这个矩形的“对角函数”.
(1)如图,在矩形ABCD中,AB∥x轴,AB=4,BC=3.
①若点 A 的坐标为(-3,2),一次函数 是矩形ABCD 的“对角函数”,则一次函数 的解析式为 ;
若反比例函数 是矩形 ABCD 的“对角函数”,求点 A 的坐标.
(2)若二次函数 是矩形ABCD 的“对角函数”,且经过A,C两点,已知点 D(-2,m)(m≠2),AB∥x轴.
①当 与矩形ABCD 有且只有两个交点时,求m 的取值范围;
已知 是 上一点,当 时,y。的最大值和最小值的差是3,求m的值.
6定义:若一个函数图象上存在横、纵坐标相等的点,则称该点为这个函数图象的“等值点”.例如,点(-1,-1)是函数y=2x+1的图象的“等值点”.
(1)①一次函数y=3x-2的图象上“等值点”的坐标为 ;
若一次函数y=kx-2(k≠0)的图象上存在“等值点”,求k的取值范围.
(2)设函数 的图象的“等值点”分别为点A,B,过点 B 作. 轴,垂足为C.当△ABC 的面积为3时,求b的值;
(3)难若函数 的图象记为 ,将其沿直线 翻折后的图象记为 此时W 的解析式为
①当W ,W 两部分组成的图象上恰有1个“等值点”时,求m 的值;
在①的结论下,若函数 (t为常数)的图象上有两个“等值点”,存在函数. (异于y ),若对于任意的自变量x,恒有点(x,y )与点( 到点(x,x)的距离相等;当t≤x≤t+1时,恒有 成立,请结合图象求t的取值范围.
专题5二次函数综合
1.解:(1)①一次函数 y=-x+6是 Rt△ABC 的“勾股函数”.理由如下:
∵∠ACB =90°,BC∥y 轴,点 C 的坐标为(1,1),AC=BC=4,∴点 A 的坐标为(5,1),点 B 的坐标为(1,5).
∵A(5,1),B(1,5)两点都在一次函数. 的图象上,
∴一次函数 是Rt△ABC 的“勾股函数”.
∵-1<0,
∴y 随x的增大而减小.
∴当1≤x≤5时,
∴Rt△ABC的“DX”值为2.
②存在.
由①,知A(5,1),B(1,5).∴k=5×1=1×5=5.
∴点A 和点 B 在同一个反比例函数 的图象上.
∴反比例函数 是Rt△ABC 的“勾股函数”.
∴k=5.
点拨由A(2,2),B(1,m)可得点C的坐标为(1,2).把点 A(2,2),C(1,2)代入 得 3x+4.对称轴为直线 在1≤x≤2的范围内,
②把点A(2,2),B(1,m)代入. 得 解得
∴对称轴为直线
∵二次函数 与 Rt△ABC 的边有第三个交点,∴点 B 在AC 上方,对称轴在A,C 两点之间.
解得2③由②,得 y 的顶点坐标为
分情况讨论:
第一种情况,点B 在点A 上方,即:m>2.
Ⅰ、当点 B 和点A 都在对称轴左侧时,
解得m≥3.
∵1>0,∴在对称轴左侧部分y 随x的增大而减小.
即
解得
Ⅱ.当对称轴在点 A 和点C 之间时,2此时yB最大,顶点最小.
…
解得 (不合题意,舍去) (不合题意,舍去).
第二种情况,点B 在点A 下方,即m<2.
Ⅰ.当点 B 和点A 都在对称轴右侧时,
解得m≤1.
∵1>0,∴在对称轴右侧部分y 随x的增大而增大.
即
解得 (不合题意,舍去).
Ⅱ.当对称轴在点 A 和点C 之间时,
解得1∵m<2,∴1月
解得 (不合题意,舍去),
综上所述,m的值为4 或 或
2.解:(1)12;3详解∵E是AD 的中点,AD=6,∴AE=3.
当t=0时
∵当t=a时,点 Q 运动到点C,点 P 运动到点E,
(2)由(1),知a=3,∴AE=3.
当0≤t≤3时,点Q在BC上运动,点 P 在AE 上运动,如图1.
∵四边形ABCD为矩形,∴BC∥AD,BC=AD=6,AB=CD=8,∠B=∠A=∠D=90°.
∵AP=l,AE=3,∴PE=3-l.
根据题意,知点 P 先到达点D,此时t=6.
当3∵AP=t,AE=3,∴PE=t-3.
∵BC+CQ=2t,
∴QD=BC+CD-(BC+CQ)=6+8-2t=14-2t.
综上所述
理由如下:
由(2),知当点 Q 在线段CD 上运动,即3∴当t=5时,S取最大值,此时
∴Q是CD 的中点.
又 E 是AD 的中点,∴EQ 是△ADC 的中位线.
∴对称轴为直线 t=5.
结合函数图象可知,
∴t 与t 关于直线t=5对称.
即
②由(4)①,得
整理,得
均使S 的值相等,
解得 或
把 代入S=-4t+12,得.
∴S 的值为
3.解:(1)①④ 详解①②③④的图象如图1所示.
由图象可知,y=-2x位于. 的图象和正方形OABC的中间,且与正方形 ABCD 只有一个公共点,y=-3x-1位于 的图象和正方形OABC的中间,且没有公共点,y=-2x+3和y=4x-1不在 和正方形OABC 之间.根据“楚河汉界线”的定义可知,直小线y=-2x和y=-3x-1是函数 与正方形OABC 的“楚河汉界线”.故①④正确.
(2)根据“楚河汉界线”的定义可知,“楚河汉界线”在△EDF与⊙O之间.
∵△EDF 与⊙O的“楚河汉界线”有且只有一条,
∴⊙O 在△EDF下方,且与⊙O 只有一个交点.
如图2,连接OD.以点O为圆心,OD 长为半径作⊙O,过点D作DG⊥x轴于点G,作⊙O的切线MD,则 MD⊥OD,∠OGD=90°.∴∠ODM=90°.
根据题意,得直线 MD 是△EDF 与⊙O 的“楚河汉界线”.
在 Rt△ODG 中,根据勾股定理,得
∴∠DMO=90°-∠MOD=∠DOG=30°.
∴OM=2OD=2×2=4.∴M(0,4).
设直线 MD 的解析式为y= mx+4.
把点 D( ,1)代入,得 解得
∴直线 MD 的解析式为
∴△EDF 与⊙O 的“楚河汉界线”的解析式为 y =
(3)当y=-2x+b的图象在
图象的上方时,如图3.
联立 得
根据“楚河汉界线”的定义可知,△≤0,
∴16-4(b-3)≤0.解得b≥7.
∵点 M(2,t)是此正方形的中心,
∴顶点A 的坐标为(0,t-2).
由顶点 A (0,t-2)不能在直线y=--2x+b的下方,得t-2≥b.
∵b≥7,∴t-2≥7.∴t≥9.
当y=-2x+b的图象在 图象的下方时,如图4.
对于抛物线 当:x=0时,y=3;
当x=4时,y=-5.
当直线 my=-2x+b经过点(0,3)时,b=3;
当直线y=-2x+b经过点(4,-5)时,-2×4+b=-5.
解得乙=3.∴b≤3.
∵点M(2,t)是此正方形的中心,∴顶点 C 的坐标为(4,t+2).
由顶点C (4,t+2)不能在直线 y=--2x+b的上方,得t+2≤-2×4+b.∴t+10≤b.
∵b≤3,∴t+10≤3.∴t≤-7.
综上所述,t的取值范围是t≤-7 或t≥9.
4.解:(1)把点 A(-1,0)代入. ,得0=-1-b+3.解得b=2.
(2)由(1),知b=2.
∴抛物线
令y=0,得 解得x=-1或x=3.
令x=0,得y=3.
∴B(3,0),C(0,3).
∵A(-1,0),∴OA=1,OC=3.
如图1,过点 M 作MH⊥x轴于点H.
∵M 是第一象限内抛物线上一点,
∴MH=-m +2m+3,AH=m-(-1)=m+1.
∵∠MAB=∠ACO,
∴tan∠MAB=tan∠ACO,即
解得 (不合题意,舍去).
∴点M 的横坐标为-
(3)①∵将抛物线 沿水平方向平移,平移后的新抛物线L 的顶点横坐标为n,
∴顶点纵坐标不变为4,图象 L 的解析式为
令x=0,得.
由(2),知C(0,3).
),
②n的取值范围是 或
详解由①,得 图象如图2.
∴当d 随n的增大而增大时,-1≤n≤0 或n≥1.
∵△ABC(不含边界)中含(0,1),(0,2),(1,1)三个横、纵坐标均为整数的点,
∴W 内恰好有两个横、纵坐标均为整数的点时,U内恰有这三个点中的两个.
Ⅰ.当-1≤n≤0,U 内恰有点(0,1),(0,2)时,
x=0,yL>2;x=1,y⊥≤1.
或
Ⅱ.当n≥1,U内恰有点(0,1),(1,1)时,x=0,1或
Ⅲ.当U 内恰有点(0,2),(1,1)时,此种情况不存在,舍去.综上所述,n的取值范围是 或
5.解: 或
详解∵点 A 的坐标为(-3,2),AB∥x轴,AB=4,BC=3,∴B(1,2),C(1,5),D(-3,5).
当一次函数 经过A,C两点时,得
解得
同理,当一次函数 经过B,D两点时,得y =
综上所述,一次函数 的解析式为 或
②∵反比例函数 是矩形 ABCD的“对角函数”,24>0,
∴当反比例函数y 的图象经过A,C两点时,设
∵AB∥x轴.AB=4,BC=3,∴c(t+4, +3).
把点 代入 得 此时方程无解.∴此种情况不存在.
当反比例函数y 的图象经过B,D两点时,设D(t,
∵AB∥x轴,AB=4,BC=3,∴B(t+4, ).
把点 代入 得
解得
当t=-8时,D(-8,-3).此时A(-8,-6).
当t=4时,D(4,6).此时A(4,3).
∴点 A 的坐标为(-8,-6)或(4,3).
(2)①∵B(-1,2),D(-2,m)(m≠2),AB∥x轴,
∴A(-2,2),C(-1,m).
经过A,C两点,
整理,得
∴顶点坐标为
与矩形ABCD 有且只有两个交点,
∴当m>2时,
当
∴m 的取值范围是m≥3或m≤1.
②由(2)①,知
当xp=m-1时,
当 时, 6m+2.
Ⅰ.当 即m≤-1时,如图1,在m-1≤x,≤m+1的范围内,y,随x,的增大而减小、
∴此时y,在 时取最大值2m ,在xp=m+1时取最小值
解得 (不合题意、舍去)、
Ⅱ.当 即 且m≠2时,如图2,在m-1≤x,≤m+1白的范围内,y,随x,的增大而增大.
∴此时y,在xp=m+1时取最大值 在x,=m--1时取最小值:2m .
解得 (不合题意,舍去).
当 即 时,
在 的范围内,y,在顶点处取最小值
Ⅲ.当
即 时,如图3,在m-1≤x,≤m+1的范围内, yp在 时取最大值
解得 (不合题意,舍去).
Ⅳ.当
即 时,如图4,在m-1≤x,≤m+1的范围内, yp在xp=m-1时取最大值2m .
解得 (不合题意,舍去),
综上所述,m的值为 或
6.解:(1)①(1,1)详解令y=x,得x=3x-2.解得x=1.
∴一次函数y=3x-2的图象上“等值点”的坐标为(1,1).
②令y=x,得x= kx-2.整理,得(k-1)x=2.
∵图象上存在“等值点”,
∴方程(k-1)x=2有解.∴k≠1.
又k≠0,∴k的取值范围是k<0或01.
(2)在函数 中,令y=x,得
解得. (负值已舍).
在函数:y=-x+b中,令y=x,得x=-x+b.
解得
∵BC⊥x轴,垂足为C,
∵△ABC 的面积为3,
整理,得
解得 或
综上所述,b的值为 或
(3)①令y=x,得 解得
∴函数 的图象上有两个“等值点”分别是(-1,-1),(2,2).
对于
令y=x,得
整理,得
∴当 时,解得 没有“等值点”,如图1.
当△≥0时,得 有等值点.
结合图象分析:当 时,W ,W 两部分组成的图象上有3个“等值点”,如图2;当-1②t的取值范围为 或
详解把m=2代入 得
∵对于任意的自变量x,恒有点(x,y )与点(x,y )到点(x,x)的距离相等,
有两个“等值点”,
有两个不相等的实数根.
解得 或
令 则
∴y 的图象的对称轴为直线
∵当t≤x≤t+1时,y >y ,即y >0,
∴y 在t≤x≤t+1上的最小值大于0.
∵--2<0,直线 在t≤x≤t+1内,且t+1-(t+ 当x=t或x=t+1时,y 取得最小值.
设 .令y =0,得 6=0.
解得
根据y 的图象,得当 或 时,y >0,即
综上所述,t的取值范围为 或
1.新考向·新定义定义:在平面直角坐标系中,若函数R 的图象经过Rt△ABC 的两个顶点,则称函数R 是 Rt△ABC 的“勾股函数”,函数 R 经过直角三角形的两个顶点的坐标分别为(x ,y ),(x ,y ),且 ,当自变量x 满足 时,函数R 的最大值记为 ymax,最小值记为ymin,令 则 h 是 Rt△ABC 的“DX”值.
已知:在平面直角坐标系中,△ABC是直角三角形,∠ACB=90°,BC∥y轴.
(1)如图,若点 C 的坐标为(1,1),AC=BC=4.
①一次函数、 是 Rt△ABC 的“勾股函数”吗 若是,请说明理由,并求出 Rt△ABC 的“DX”值;若不是,请说明理由;
是否存在反比例函数 是 Rt△ABC的“勾股函数” 若存在,求出k 的值;若不存在,请说明理由.
(2)已知点 A 的坐标为(2,2),点 B 的坐标为(1,m),二次函数 是 Rt△ABC 的“勾股函数”,其中∠ACB=90°.
①若二次函数 经过A,C 两点,则 Rt△ABC 的“DX”值h= ;
若二次函数 经过A,B 两点,且与 Rt△ABC 的边有第三个交点,求m 的取值范围;
③若二次函数 经过A,B 两点,且 Rt△ABC 的“DX”值 求m 的值.
2.如图1,在矩形ABCD 中,已知. ,E 是 AD 的中点,动点 P 从点 A 出发,以每秒1个单位长度的速度沿AD 向点 D 运动,同时动点Q 从点B 出发,以每秒2个单位长度的速度沿折线 BC-CD 运动,当其中一个点到达点 D 时,另一个点也随之停止运动,连接PQ,EQ,设动点 P 运动的时间为t s, 的面积为S,图2是S 关于t的函数关系图象.
(1)填空:
(2)求S 关于t的函数解析式,并写出自变量t 的取值范围;
(3)当点 Q 在线段CD 上运动且S 取最大值时,判断线段 EQ 与对角线AC 的关系,并说明理由;
(4)在整个运动过程中,存在某3个时刻 使得 S 的值相等.
①求 的值;
当 时,求S 的值.
3.中国象棋棋盘上双方的分界处称为“楚河汉界”,以“楚河汉界”比喻两军对垒的分界线,数学中为了对两个图形进行分界,在平面直角坐标系中,对“楚河汉界线”给出如下定义: 是图形G 上的任意一点, 是图形 上的任意一点,若直线l:y=kx+b(k≠0)满足 且 则称直线 是图形 与图形 的“楚河汉界线”.例如:如图1,直线l:y=--x-4是函数 的图象与正方形 OABC 的一条“楚河汉界线”.
(1)在①y=-2x;y=4x-1;③y=-2x+3;④y=-3x-1中,是图1中函数 的图象与正方形 OABC 的“楚河汉界线”的有 ;(填序号)
(2)如图2,在第一象限内,等腰 的两腰分别与坐标轴平行,直角顶点 D 的坐标为 ,若△EDF 与⊙O 的“楚河汉界线”有且只有一条,求此“楚河汉界线”的解析式;
(3)正方形 的一边在y轴上,其他三边都在y轴的右侧,点M(2,t)是此正方形的中心,若存在直线 y=-2x+b是函数 的图象与正方形 的“楚河汉界线”,求t 的取值范围.
4.在平面直角坐标系中,抛物线 与x轴相交于点 A(-1,0)和点 B,与 y 轴相交于点 C、
(1)求b的值;
(2)如图1,M是第一象限内抛物线上一点,已知∠MAB=∠ACO,求点 M 的横坐标;
(3)将此抛物线沿水平方向平移,得到的新抛物线记为L,L与y轴相交于点N,设L 的顶点横坐标为n,NC 的长为d、
①求 d 关于n的函数解析式;
如图2,L 与x轴围成的区域记为U,U与△ABC内部重合的区域(不含边界)记为W,当d随n的增大而增大,且W 内恰好有两个横、纵坐标均为整数的点时,直接写出n的取值范围.
全国视野
考法拓展
5.新新考向·新定义若函数y经过矩形一条对角线上的两个端点,则称函数y 为这个矩形的“对角函数”.
(1)如图,在矩形ABCD中,AB∥x轴,AB=4,BC=3.
①若点 A 的坐标为(-3,2),一次函数 是矩形ABCD 的“对角函数”,则一次函数 的解析式为 ;
若反比例函数 是矩形 ABCD 的“对角函数”,求点 A 的坐标.
(2)若二次函数 是矩形ABCD 的“对角函数”,且经过A,C两点,已知点 D(-2,m)(m≠2),AB∥x轴.
①当 与矩形ABCD 有且只有两个交点时,求m 的取值范围;
已知 是 上一点,当 时,y。的最大值和最小值的差是3,求m的值.
6定义:若一个函数图象上存在横、纵坐标相等的点,则称该点为这个函数图象的“等值点”.例如,点(-1,-1)是函数y=2x+1的图象的“等值点”.
(1)①一次函数y=3x-2的图象上“等值点”的坐标为 ;
若一次函数y=kx-2(k≠0)的图象上存在“等值点”,求k的取值范围.
(2)设函数 的图象的“等值点”分别为点A,B,过点 B 作. 轴,垂足为C.当△ABC 的面积为3时,求b的值;
(3)难若函数 的图象记为 ,将其沿直线 翻折后的图象记为 此时W 的解析式为
①当W ,W 两部分组成的图象上恰有1个“等值点”时,求m 的值;
在①的结论下,若函数 (t为常数)的图象上有两个“等值点”,存在函数. (异于y ),若对于任意的自变量x,恒有点(x,y )与点( 到点(x,x)的距离相等;当t≤x≤t+1时,恒有 成立,请结合图象求t的取值范围.
专题5二次函数综合
1.解:(1)①一次函数 y=-x+6是 Rt△ABC 的“勾股函数”.理由如下:
∵∠ACB =90°,BC∥y 轴,点 C 的坐标为(1,1),AC=BC=4,∴点 A 的坐标为(5,1),点 B 的坐标为(1,5).
∵A(5,1),B(1,5)两点都在一次函数. 的图象上,
∴一次函数 是Rt△ABC 的“勾股函数”.
∵-1<0,
∴y 随x的增大而减小.
∴当1≤x≤5时,
∴Rt△ABC的“DX”值为2.
②存在.
由①,知A(5,1),B(1,5).∴k=5×1=1×5=5.
∴点A 和点 B 在同一个反比例函数 的图象上.
∴反比例函数 是Rt△ABC 的“勾股函数”.
∴k=5.
点拨由A(2,2),B(1,m)可得点C的坐标为(1,2).把点 A(2,2),C(1,2)代入 得 3x+4.对称轴为直线 在1≤x≤2的范围内,
②把点A(2,2),B(1,m)代入. 得 解得
∴对称轴为直线
∵二次函数 与 Rt△ABC 的边有第三个交点,∴点 B 在AC 上方,对称轴在A,C 两点之间.
解得2
分情况讨论:
第一种情况,点B 在点A 上方,即:m>2.
Ⅰ、当点 B 和点A 都在对称轴左侧时,
解得m≥3.
∵1>0,∴在对称轴左侧部分y 随x的增大而减小.
即
解得
Ⅱ.当对称轴在点 A 和点C 之间时,2
…
解得 (不合题意,舍去) (不合题意,舍去).
第二种情况,点B 在点A 下方,即m<2.
Ⅰ.当点 B 和点A 都在对称轴右侧时,
解得m≤1.
∵1>0,∴在对称轴右侧部分y 随x的增大而增大.
即
解得 (不合题意,舍去).
Ⅱ.当对称轴在点 A 和点C 之间时,
解得1
解得 (不合题意,舍去),
综上所述,m的值为4 或 或
2.解:(1)12;3详解∵E是AD 的中点,AD=6,∴AE=3.
当t=0时
∵当t=a时,点 Q 运动到点C,点 P 运动到点E,
(2)由(1),知a=3,∴AE=3.
当0≤t≤3时,点Q在BC上运动,点 P 在AE 上运动,如图1.
∵四边形ABCD为矩形,∴BC∥AD,BC=AD=6,AB=CD=8,∠B=∠A=∠D=90°.
∵AP=l,AE=3,∴PE=3-l.
根据题意,知点 P 先到达点D,此时t=6.
当3
∵BC+CQ=2t,
∴QD=BC+CD-(BC+CQ)=6+8-2t=14-2t.
综上所述
理由如下:
由(2),知当点 Q 在线段CD 上运动,即3
∴Q是CD 的中点.
又 E 是AD 的中点,∴EQ 是△ADC 的中位线.
∴对称轴为直线 t=5.
结合函数图象可知,
∴t 与t 关于直线t=5对称.
即
②由(4)①,得
整理,得
均使S 的值相等,
解得 或
把 代入S=-4t+12,得.
∴S 的值为
3.解:(1)①④ 详解①②③④的图象如图1所示.
由图象可知,y=-2x位于. 的图象和正方形OABC的中间,且与正方形 ABCD 只有一个公共点,y=-3x-1位于 的图象和正方形OABC的中间,且没有公共点,y=-2x+3和y=4x-1不在 和正方形OABC 之间.根据“楚河汉界线”的定义可知,直小线y=-2x和y=-3x-1是函数 与正方形OABC 的“楚河汉界线”.故①④正确.
(2)根据“楚河汉界线”的定义可知,“楚河汉界线”在△EDF与⊙O之间.
∵△EDF 与⊙O的“楚河汉界线”有且只有一条,
∴⊙O 在△EDF下方,且与⊙O 只有一个交点.
如图2,连接OD.以点O为圆心,OD 长为半径作⊙O,过点D作DG⊥x轴于点G,作⊙O的切线MD,则 MD⊥OD,∠OGD=90°.∴∠ODM=90°.
根据题意,得直线 MD 是△EDF 与⊙O 的“楚河汉界线”.
在 Rt△ODG 中,根据勾股定理,得
∴∠DMO=90°-∠MOD=∠DOG=30°.
∴OM=2OD=2×2=4.∴M(0,4).
设直线 MD 的解析式为y= mx+4.
把点 D( ,1)代入,得 解得
∴直线 MD 的解析式为
∴△EDF 与⊙O 的“楚河汉界线”的解析式为 y =
(3)当y=-2x+b的图象在
图象的上方时,如图3.
联立 得
根据“楚河汉界线”的定义可知,△≤0,
∴16-4(b-3)≤0.解得b≥7.
∵点 M(2,t)是此正方形的中心,
∴顶点A 的坐标为(0,t-2).
由顶点 A (0,t-2)不能在直线y=--2x+b的下方,得t-2≥b.
∵b≥7,∴t-2≥7.∴t≥9.
当y=-2x+b的图象在 图象的下方时,如图4.
对于抛物线 当:x=0时,y=3;
当x=4时,y=-5.
当直线 my=-2x+b经过点(0,3)时,b=3;
当直线y=-2x+b经过点(4,-5)时,-2×4+b=-5.
解得乙=3.∴b≤3.
∵点M(2,t)是此正方形的中心,∴顶点 C 的坐标为(4,t+2).
由顶点C (4,t+2)不能在直线 y=--2x+b的上方,得t+2≤-2×4+b.∴t+10≤b.
∵b≤3,∴t+10≤3.∴t≤-7.
综上所述,t的取值范围是t≤-7 或t≥9.
4.解:(1)把点 A(-1,0)代入. ,得0=-1-b+3.解得b=2.
(2)由(1),知b=2.
∴抛物线
令y=0,得 解得x=-1或x=3.
令x=0,得y=3.
∴B(3,0),C(0,3).
∵A(-1,0),∴OA=1,OC=3.
如图1,过点 M 作MH⊥x轴于点H.
∵M 是第一象限内抛物线上一点,
∴MH=-m +2m+3,AH=m-(-1)=m+1.
∵∠MAB=∠ACO,
∴tan∠MAB=tan∠ACO,即
解得 (不合题意,舍去).
∴点M 的横坐标为-
(3)①∵将抛物线 沿水平方向平移,平移后的新抛物线L 的顶点横坐标为n,
∴顶点纵坐标不变为4,图象 L 的解析式为
令x=0,得.
由(2),知C(0,3).
),
②n的取值范围是 或
详解由①,得 图象如图2.
∴当d 随n的增大而增大时,-1≤n≤0 或n≥1.
∵△ABC(不含边界)中含(0,1),(0,2),(1,1)三个横、纵坐标均为整数的点,
∴W 内恰好有两个横、纵坐标均为整数的点时,U内恰有这三个点中的两个.
Ⅰ.当-1≤n≤0,U 内恰有点(0,1),(0,2)时,
x=0,yL>2;x=1,y⊥≤1.
或
Ⅱ.当n≥1,U内恰有点(0,1),(1,1)时,x=0,1
Ⅲ.当U 内恰有点(0,2),(1,1)时,此种情况不存在,舍去.综上所述,n的取值范围是 或
5.解: 或
详解∵点 A 的坐标为(-3,2),AB∥x轴,AB=4,BC=3,∴B(1,2),C(1,5),D(-3,5).
当一次函数 经过A,C两点时,得
解得
同理,当一次函数 经过B,D两点时,得y =
综上所述,一次函数 的解析式为 或
②∵反比例函数 是矩形 ABCD的“对角函数”,24>0,
∴当反比例函数y 的图象经过A,C两点时,设
∵AB∥x轴.AB=4,BC=3,∴c(t+4, +3).
把点 代入 得 此时方程无解.∴此种情况不存在.
当反比例函数y 的图象经过B,D两点时,设D(t,
∵AB∥x轴,AB=4,BC=3,∴B(t+4, ).
把点 代入 得
解得
当t=-8时,D(-8,-3).此时A(-8,-6).
当t=4时,D(4,6).此时A(4,3).
∴点 A 的坐标为(-8,-6)或(4,3).
(2)①∵B(-1,2),D(-2,m)(m≠2),AB∥x轴,
∴A(-2,2),C(-1,m).
经过A,C两点,
整理,得
∴顶点坐标为
与矩形ABCD 有且只有两个交点,
∴当m>2时,
当
∴m 的取值范围是m≥3或m≤1.
②由(2)①,知
当xp=m-1时,
当 时, 6m+2.
Ⅰ.当 即m≤-1时,如图1,在m-1≤x,≤m+1的范围内,y,随x,的增大而减小、
∴此时y,在 时取最大值2m ,在xp=m+1时取最小值
解得 (不合题意、舍去)、
Ⅱ.当 即 且m≠2时,如图2,在m-1≤x,≤m+1白的范围内,y,随x,的增大而增大.
∴此时y,在xp=m+1时取最大值 在x,=m--1时取最小值:2m .
解得 (不合题意,舍去).
当 即 时,
在 的范围内,y,在顶点处取最小值
Ⅲ.当
即 时,如图3,在m-1≤x,≤m+1的范围内, yp在 时取最大值
解得 (不合题意,舍去).
Ⅳ.当
即 时,如图4,在m-1≤x,≤m+1的范围内, yp在xp=m-1时取最大值2m .
解得 (不合题意,舍去),
综上所述,m的值为 或
6.解:(1)①(1,1)详解令y=x,得x=3x-2.解得x=1.
∴一次函数y=3x-2的图象上“等值点”的坐标为(1,1).
②令y=x,得x= kx-2.整理,得(k-1)x=2.
∵图象上存在“等值点”,
∴方程(k-1)x=2有解.∴k≠1.
又k≠0,∴k的取值范围是k<0或0
(2)在函数 中,令y=x,得
解得. (负值已舍).
在函数:y=-x+b中,令y=x,得x=-x+b.
解得
∵BC⊥x轴,垂足为C,
∵△ABC 的面积为3,
整理,得
解得 或
综上所述,b的值为 或
(3)①令y=x,得 解得
∴函数 的图象上有两个“等值点”分别是(-1,-1),(2,2).
对于
令y=x,得
整理,得
∴当 时,解得 没有“等值点”,如图1.
当△≥0时,得 有等值点.
结合图象分析:当 时,W ,W 两部分组成的图象上有3个“等值点”,如图2;当-1
详解把m=2代入 得
∵对于任意的自变量x,恒有点(x,y )与点(x,y )到点(x,x)的距离相等,
有两个“等值点”,
有两个不相等的实数根.
解得 或
令 则
∴y 的图象的对称轴为直线
∵当t≤x≤t+1时,y >y ,即y >0,
∴y 在t≤x≤t+1上的最小值大于0.
∵--2<0,直线 在t≤x≤t+1内,且t+1-(t+ 当x=t或x=t+1时,y 取得最小值.
设 .令y =0,得 6=0.
解得
根据y 的图象,得当 或 时,y >0,即
综上所述,t的取值范围为 或
同课章节目录
