【江苏省各地区期末真题汇编】热点题型分类突破:填空题(含解析)-2024-2025学年数学七年级下册苏科版(2024)
文档属性
| 名称 | 【江苏省各地区期末真题汇编】热点题型分类突破:填空题(含解析)-2024-2025学年数学七年级下册苏科版(2024) |  | |
| 格式 | docx | ||
| 文件大小 | 432.2KB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 苏科版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2025-05-30 15:21:41 | ||
图片预览




文档简介
中小学教育资源及组卷应用平台
【江苏省各地区期末真题汇编】热点题型分类突破:填空题-2024-2024学年数学七年级下册苏科版(2024)
1.(2024春 宝应县期末)已知a=255,b=522,则a,b的大小关系是 (请用字母表示,并用“<”连接).
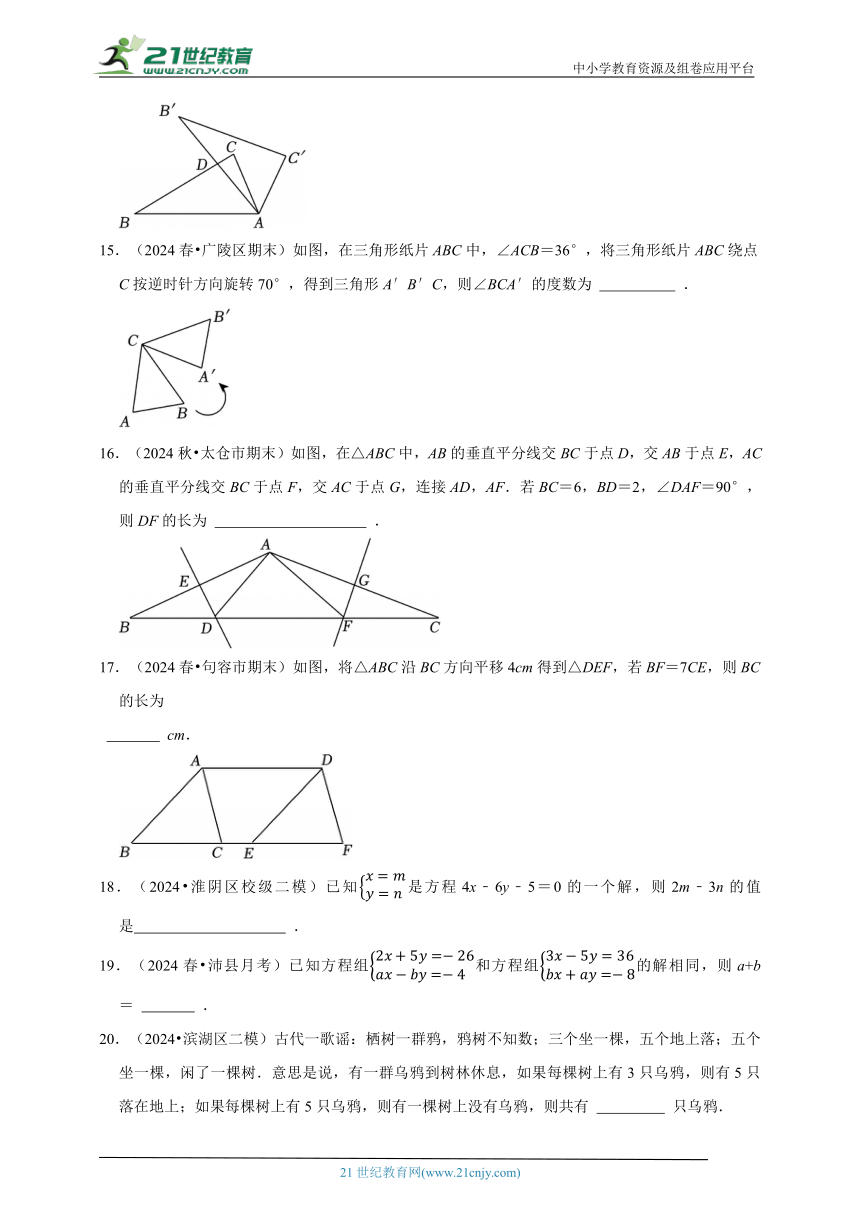
2.(2024春 赣榆区期末)已知ax=8,ay=32,则a2x﹣y的值为 .
3.(2024春 锡山区校级月考)若m=2x+1,n=4x+2x,用含m的代数式表示n,则n= .
4.(2013春 崇安区校级期末)已知2m+3n=3,则4m 8n的值为 .
5.(2020春 洪泽区期末)计算x4÷x的结果等于 .
6.(2024春 东台市月考)已知m+n=5,m﹣n=﹣1,则m2﹣n2= .
7.(2024春 锡山区校级期末)如果代数式(mx﹣3)(x+2)的展开式不含x的一次项,那么m为 .
8.(2024春 广陵区期末)若(x+p)(x﹣4)的展开式中不含有x项,则p= .
9.(2024春 锡山区期末)如图,现有正方形卡片A类,B类和长方形卡片C类若干张,若要拼一个长为(2a+b),宽为(a+3b)的大长方形,则需C类卡片 张.
10.(2024春 工业园区校级月考)计算:2024×2026﹣20242= .
11.(2024春 江阴市期末)设a=x﹣2023,b=x﹣2024,c=x﹣2024.若a2+b2=16,则c2的值是 .
12.(2024春 建邺区校级期末)若x2﹣5x﹣2=0,则(x﹣1)(x﹣2)(x﹣3)(x﹣4)= .
13.(2024春 工业园区校级月考)如图,将△ABC沿BC方向平移3cm得到△DEF(其中点A,B,C分别与点D,E,F对应),若CE=6cm,则BF= cm.
14.(2024 梁溪区二模)如图,△ABC中,∠B=28°,将△ABC绕点A顺时针旋转52°得△AB′C′,AB′与BC交于D,则∠ADC= °.
15.(2024春 广陵区期末)如图,在三角形纸片ABC中,∠ACB=36°,将三角形纸片ABC绕点C按逆时针方向旋转70°,得到三角形A′B′C,则∠BCA′的度数为 .
16.(2024秋 太仓市期末)如图,在△ABC中,AB的垂直平分线交BC于点D,交AB于点E,AC的垂直平分线交BC于点F,交AC于点G,连接AD,AF.若BC=6,BD=2,∠DAF=90°,则DF的长为 .
17.(2024春 句容市期末)如图,将△ABC沿BC方向平移4cm得到△DEF,若BF=7CE,则BC的长为
cm.
18.(2024 淮阴区校级二模)已知是方程4x﹣6y﹣5=0的一个解,则2m﹣3n的值是 .
19.(2024春 沛县月考)已知方程组和方程组的解相同,则a+b= .
20.(2024 滨湖区二模)古代一歌谣:栖树一群鸦,鸦树不知数;三个坐一棵,五个地上落;五个坐一棵,闲了一棵树.意思是说,有一群乌鸦到树林休息,如果每棵树上有3只乌鸦,则有5只落在地上;如果每棵树上有5只乌鸦,则有一棵树上没有乌鸦,则共有 只乌鸦.
21.(2024春 玄武区校级月考)已知方程组的解是,则方程组的解为 .
22.(2024春 高新区校级月考)如果方程组和解的相同,则nm= .
23.(2024春 高新区校级月考)对于有理数x、y,定义新运算☆:x☆y=ax+by,其中a、b是常数.已知1☆2=1,(﹣3)☆3=6,则2☆(﹣5)的值是 .
24.(2024 高邮市二模)古代算书《四元玉鉴》中有“两果问价”问题:“甜果九个十一文钱,苦果七个四文钱,九百九十九文钱,甜果苦果买一千.试问甜苦果几个?”该问题意思是:已知十一文钱可买九个甜果,四文钱可买七个苦果,九百九十九文钱买了甜果和苦果共一千个,那么甜果、苦果各买了多少个?设甜果买了x个,苦果买了y个,根据题意,可列方程组是 .
25.(2024 宿迁模拟)科学研究表明:树叶在光合作用后产生的分泌物能够吸附空气中的悬浮颗粒物,具有滞尘净化空气的作用,已知一片银杏树叶一年的平均滞尘量比一片国槐树叶一年的平均滞尘量的2倍少4毫克,两片银杏树叶与三片国槐树叶一年的平均滞尘总量为146毫克.设一片银杏树叶一年的平均滞尘量为x毫克,一片国槐树叶一年的平均滞尘量为y毫克.依据题意,可列方程组为 .
26.(2024春 海陵区期末)若关于x,y的二元一次方程组的解为,则关于m,n二元一次方程组的解为 .
27.(2024春 江阴市月考)如图,这是一个计算机程序,规定从输入一个x值到判断结果是否≥15为一次运行过程,如果程序运行两次就停止,那么x的取值范围是 .
28.(2024春 东台市月考)若不等式组无解,则m的取值范围是 .
29.(2024春 玄武区校级月考)某商场促销方案规定:单笔消费金额每满100元立减10元.例如,单笔消费金额为208元时,立减20元.甲在该商场单笔购买2件A商品,立减了20元;乙在该商场单笔购买2件A商品与1件B商品,立减了30元.若B商品的单价是整数元,则它的最大值是 .
30.(2024秋 鼓楼区期末)已知三条不同的直线a,b,c在同一平面内,下列四个命题:
①如果a∥b,a⊥c,那么b⊥c; ②如果b∥a,c∥a,那么b∥c;
③如果b⊥a,c⊥a,那么b⊥c; ④如果b⊥a,c⊥a,那么b∥c.
其中正确的是 .(填写序号)
【江苏省各地区期末真题汇编】热点题型分类突破:填空题-2024-2024学年数学七年级下册苏科版(2024)
参考答案与试题解析
1.(2024春 宝应县期末)已知a=255,b=522,则a,b的大小关系是 b<a. (请用字母表示,并用“<”连接).
【解答】解:a=255=(25)11=3211,
b=522=(52)11=2511,
∵2511<3211,
∴522<255,
故答案为:b<a.
2.(2024春 赣榆区期末)已知ax=8,ay=32,则a2x﹣y的值为 2 .
【解答】解:∵ax=8,ay=32,
∴a2x﹣y=a2x÷ay=(ax)2÷ay=82÷32=2,
故答案为:2.
3.(2024春 锡山区校级月考)若m=2x+1,n=4x+2x,用含m的代数式表示n,则n= m2﹣m .
【解答】解:∵m=2x+1,
∴2x=m﹣1,
∴n=4x+2x
=(22)x+2x
=(2x)2+2x
=(m﹣1)2+m﹣1
=m2﹣2m+1+m﹣1
=m2﹣m,
故答案为:m2﹣m.
4.(2013春 崇安区校级期末)已知2m+3n=3,则4m 8n的值为 8 .
【解答】解:4m 8n=22m×23n=22m+3n,
∵2m+3n=3,
∴22m+3n=23=8.
故答案为8.
5.(2020春 洪泽区期末)计算x4÷x的结果等于 x3 .
【解答】解:x4÷x=x4﹣1=x3.
故答案为:x3.
6.(2024春 东台市月考)已知m+n=5,m﹣n=﹣1,则m2﹣n2= ﹣5 .
【解答】解:∵m+n=5,m﹣n=﹣1,
∴m2﹣n2=(m+n)(m﹣n)=5×(﹣1)=﹣5,
故答案为:﹣5.
7.(2024春 锡山区校级期末)如果代数式(mx﹣3)(x+2)的展开式不含x的一次项,那么m为 .
【解答】解:∵多项式(mx﹣3)(x+2)=mx2+(2m﹣3)x﹣6不含x的一次项,
∴2m﹣3=0,
解得m.
故答案为:.
8.(2024春 广陵区期末)若(x+p)(x﹣4)的展开式中不含有x项,则p= 4 .
【解答】解:∵多项式(x+p)(x﹣4)=x2+(p﹣4)x﹣4p不含x项,
∴p﹣4=0,
解得p=4.
故答案为:4.
9.(2024春 锡山区期末)如图,现有正方形卡片A类,B类和长方形卡片C类若干张,若要拼一个长为(2a+b),宽为(a+3b)的大长方形,则需C类卡片 7 张.
【解答】解:(2a+b)(a+3b)
=2a2+6ab+ab+3b2
=2a2+7ab+3b2,
根据题意得A类卡片的面积是a2,B类卡片的面积是b2,C类卡片的面积是ab,
所以需C类卡片7张,
故答案为:7.
10.(2024春 工业园区校级月考)计算:2024×2026﹣20242= ﹣1 .
【解答】解:2024×2026﹣20242
=(2024﹣1)(2024+1)﹣20242
=20242﹣1﹣20242
=﹣1.
11.(2024春 江阴市期末)设a=x﹣2023,b=x﹣2024,c=x﹣2024.若a2+b2=16,则c2的值是 7 .
【解答】解:由条件可知a﹣1=x﹣2024=c,b+1=x﹣2024=c,a﹣b=2,
∵(a﹣b)2=a2+b2﹣2ab,a2+b2=16,
∴22=16﹣2ab,则ab=6,
∴c2=(a﹣1)(b+1)
=ab+(a﹣b)﹣1
=6+2﹣1
=7,
故答案为:7.
12.(2024春 建邺区校级期末)若x2﹣5x﹣2=0,则(x﹣1)(x﹣2)(x﹣3)(x﹣4)= 48 .
【解答】解:∵x2﹣5x﹣2=0,
∴x2﹣5x=2,
∴(x﹣1)(x﹣2)(x﹣3)(x﹣4)
=[(x﹣1)(x﹣4)][(x﹣2)(x﹣3)]
=(x2﹣5x+4)(x2﹣5x+6)
=(2+4)×(2+6)
=6×8
=48,
故答案为:48.
13.(2024春 工业园区校级月考)如图,将△ABC沿BC方向平移3cm得到△DEF(其中点A,B,C分别与点D,E,F对应),若CE=6cm,则BF= 12 cm.
【解答】解:由题知,
因为△DEF由△ABC沿BC方向平移3cm得到,
所以BE=CF=3cm.
又因为CE=6cm,
所以BF=BE+CE+CF=3+6+3=12(cm).
故答案为:12.
14.(2024 梁溪区二模)如图,△ABC中,∠B=28°,将△ABC绕点A顺时针旋转52°得△AB′C′,AB′与BC交于D,则∠ADC= 80 °.
【解答】解:∵△ABC绕点A顺时针旋转52°得△AB′C′,
∴∠BAB′=52°,
∵∠B=28°,
∴∠ADB=180°﹣∠BAB′﹣∠B=100°,
∴∠ADC=180°﹣∠ADB=80°.
故答案为:80.
15.(2024春 广陵区期末)如图,在三角形纸片ABC中,∠ACB=36°,将三角形纸片ABC绕点C按逆时针方向旋转70°,得到三角形A′B′C,则∠BCA′的度数为 34° .
【解答】解:由题意知∠ACA′=70°,
∵∠ACB=36°,
∴∠BCA′=∠ACA′﹣∠ACB=34°,
故答案为:34°.
16.(2024秋 太仓市期末)如图,在△ABC中,AB的垂直平分线交BC于点D,交AB于点E,AC的垂直平分线交BC于点F,交AC于点G,连接AD,AF.若BC=6,BD=2,∠DAF=90°,则DF的长为 .
【解答】解:∵DE是AB的垂直平分线,BD=2,
∴AD=BD=2,
∵GF是AC的垂直平分线,
∴FA=FC,
∵BC=6,
∴FA=FC=4﹣DF,
∵∠DAF=90°,
∴DF2=AD2+AF2,即DF2=22+(4﹣DF)2,
解得:DF,
故答案为:.
17.(2024春 句容市期末)如图,将△ABC沿BC方向平移4cm得到△DEF,若BF=7CE,则BC的长为 3 cm.
【解答】解:由平移可得,BE=CF=AD=4cm,
∵BF=BE+EF=4+(CF﹣CE)=4+4﹣CE=7CE,
∴CE=1cm,
∴BC=BE﹣CE=4﹣1=3(cm),
故答案为:3.
18.(2024 淮阴区校级二模)已知是方程4x﹣6y﹣5=0的一个解,则2m﹣3n的值是 .
【解答】解:把代入方程4x﹣6y﹣5=0中,得4m﹣6n﹣5=0,
即2(2m﹣3n)=5,
∴2m﹣3n,
故答案为:.
19.(2024春 沛县月考)已知方程组和方程组的解相同,则a+b= 0 .
【解答】解:∵方程组和方程组的解相同,
联立得:,
①+②得:5x=10,即x=2,
把x=2代入①得:4+5y=﹣26,
解得:y=﹣6,
代入得:,
解得:a=1,b=﹣1,
则a+b=﹣1+1=0,
故答案为:0.
20.(2024 滨湖区二模)古代一歌谣:栖树一群鸦,鸦树不知数;三个坐一棵,五个地上落;五个坐一棵,闲了一棵树.意思是说,有一群乌鸦到树林休息,如果每棵树上有3只乌鸦,则有5只落在地上;如果每棵树上有5只乌鸦,则有一棵树上没有乌鸦,则共有 20 只乌鸦.
【解答】解:设乌鸦有x只,树有y棵,依题得
,
解得,
故答案为:20.
21.(2024春 玄武区校级月考)已知方程组的解是,则方程组的解为 .
【解答】解:∵的解是,
∴,
由①得:x=1,
由②得:y=4,
∴方程组的解为,
故答案为:.
22.(2024春 高新区校级月考)如果方程组和解的相同,则nm= 1 .
【解答】解:∵方程组和解的相同,
∴,
解得:,
∴2﹣m=2,2n﹣1=2,
解得:,
∴.
故答案为:1.
23.(2024春 高新区校级月考)对于有理数x、y,定义新运算☆:x☆y=ax+by,其中a、b是常数.已知1☆2=1,(﹣3)☆3=6,则2☆(﹣5)的值是 ﹣7 .
【解答】解:∵x☆y=ax+by,1☆2=1,(﹣3)☆3=6,
∴,
①×3得:3a+6b=3③,
②+③得:b=1,
把b=1代入①得:a=﹣1,
∴x☆y=﹣x+y,
∴2☆(﹣5)=﹣2﹣5=﹣7,
故答案为:﹣7.
24.(2024 高邮市二模)古代算书《四元玉鉴》中有“两果问价”问题:“甜果九个十一文钱,苦果七个四文钱,九百九十九文钱,甜果苦果买一千.试问甜苦果几个?”该问题意思是:已知十一文钱可买九个甜果,四文钱可买七个苦果,九百九十九文钱买了甜果和苦果共一千个,那么甜果、苦果各买了多少个?设甜果买了x个,苦果买了y个,根据题意,可列方程组是 .
【解答】解:∵买了甜果和苦果共一千个,
∴x+y=1000;
∵买甜果和苦果共花了999文钱,
∴xy=999,
∴根据题意可列方程组:,
故答案为:.
25.(2024 宿迁模拟)科学研究表明:树叶在光合作用后产生的分泌物能够吸附空气中的悬浮颗粒物,具有滞尘净化空气的作用,已知一片银杏树叶一年的平均滞尘量比一片国槐树叶一年的平均滞尘量的2倍少4毫克,两片银杏树叶与三片国槐树叶一年的平均滞尘总量为146毫克.设一片银杏树叶一年的平均滞尘量为x毫克,一片国槐树叶一年的平均滞尘量为y毫克.依据题意,可列方程组为 .
【解答】解:由题意得:.
故答案为:.
26.(2024春 海陵区期末)若关于x,y的二元一次方程组的解为,则关于m,n二元一次方程组的解为 .
【解答】解:设m+1=h,n﹣2=g,
可化为:,
则:可化为,
又∵的解为,
∴,
∴m+1=4,n﹣2=﹣2,
解得:m=3,n=0.
故答案为:.
27.(2024春 江阴市月考)如图,这是一个计算机程序,规定从输入一个x值到判断结果是否≥15为一次运行过程,如果程序运行两次就停止,那么x的取值范围是 x .
【解答】解:根据题意得:,
解得:x,
∴x的取值范围是x.
故答案为:x.
28.(2024春 东台市月考)若不等式组无解,则m的取值范围是 m≤2 .
【解答】解:,
解不等式2x﹣4>0,得x>2,
∴不等式组的解集为2<x<m,
∵不等式组无解,
∴m≤2,
故答案为:m≤2.
29.(2024春 玄武区校级月考)某商场促销方案规定:单笔消费金额每满100元立减10元.例如,单笔消费金额为208元时,立减20元.甲在该商场单笔购买2件A商品,立减了20元;乙在该商场单笔购买2件A商品与1件B商品,立减了30元.若B商品的单价是整数元,则它的最大值是 199 .
【解答】解:由题意可得,2件A产品的消费金额满足:200≤2件A产品的价格<300,
300≤2件A产品的价格+1件B产品的价格<400,
设B产品的单价为x元,
300≤200+x<400,
解得:100≤x<200,
∵B产品的单价为整数,
∴B商品的单价的最大值为199元.
故答案为:199.
30.(2024秋 鼓楼区期末)已知三条不同的直线a,b,c在同一平面内,下列四个命题:
①如果a∥b,a⊥c,那么b⊥c; ②如果b∥a,c∥a,那么b∥c;
③如果b⊥a,c⊥a,那么b⊥c; ④如果b⊥a,c⊥a,那么b∥c.
其中正确的是 ①②④ .(填写序号)
【解答】解:在同一个平面内,①如果a∥b,a⊥c,那么b⊥c;
②如果b∥a,c∥a,那么b∥c;
③如果b⊥a,c⊥a,那么b∥c;
④如果b⊥a,c⊥a,那么b∥c,
故答案为:①②④.
21世纪教育网 www.21cnjy.com 精品试卷·第 2 页 (共 2 页)
21世纪教育网(www.21cnjy.com)
【江苏省各地区期末真题汇编】热点题型分类突破:填空题-2024-2024学年数学七年级下册苏科版(2024)
1.(2024春 宝应县期末)已知a=255,b=522,则a,b的大小关系是 (请用字母表示,并用“<”连接).
2.(2024春 赣榆区期末)已知ax=8,ay=32,则a2x﹣y的值为 .
3.(2024春 锡山区校级月考)若m=2x+1,n=4x+2x,用含m的代数式表示n,则n= .
4.(2013春 崇安区校级期末)已知2m+3n=3,则4m 8n的值为 .
5.(2020春 洪泽区期末)计算x4÷x的结果等于 .
6.(2024春 东台市月考)已知m+n=5,m﹣n=﹣1,则m2﹣n2= .
7.(2024春 锡山区校级期末)如果代数式(mx﹣3)(x+2)的展开式不含x的一次项,那么m为 .
8.(2024春 广陵区期末)若(x+p)(x﹣4)的展开式中不含有x项,则p= .
9.(2024春 锡山区期末)如图,现有正方形卡片A类,B类和长方形卡片C类若干张,若要拼一个长为(2a+b),宽为(a+3b)的大长方形,则需C类卡片 张.
10.(2024春 工业园区校级月考)计算:2024×2026﹣20242= .
11.(2024春 江阴市期末)设a=x﹣2023,b=x﹣2024,c=x﹣2024.若a2+b2=16,则c2的值是 .
12.(2024春 建邺区校级期末)若x2﹣5x﹣2=0,则(x﹣1)(x﹣2)(x﹣3)(x﹣4)= .
13.(2024春 工业园区校级月考)如图,将△ABC沿BC方向平移3cm得到△DEF(其中点A,B,C分别与点D,E,F对应),若CE=6cm,则BF= cm.
14.(2024 梁溪区二模)如图,△ABC中,∠B=28°,将△ABC绕点A顺时针旋转52°得△AB′C′,AB′与BC交于D,则∠ADC= °.
15.(2024春 广陵区期末)如图,在三角形纸片ABC中,∠ACB=36°,将三角形纸片ABC绕点C按逆时针方向旋转70°,得到三角形A′B′C,则∠BCA′的度数为 .
16.(2024秋 太仓市期末)如图,在△ABC中,AB的垂直平分线交BC于点D,交AB于点E,AC的垂直平分线交BC于点F,交AC于点G,连接AD,AF.若BC=6,BD=2,∠DAF=90°,则DF的长为 .
17.(2024春 句容市期末)如图,将△ABC沿BC方向平移4cm得到△DEF,若BF=7CE,则BC的长为
cm.
18.(2024 淮阴区校级二模)已知是方程4x﹣6y﹣5=0的一个解,则2m﹣3n的值是 .
19.(2024春 沛县月考)已知方程组和方程组的解相同,则a+b= .
20.(2024 滨湖区二模)古代一歌谣:栖树一群鸦,鸦树不知数;三个坐一棵,五个地上落;五个坐一棵,闲了一棵树.意思是说,有一群乌鸦到树林休息,如果每棵树上有3只乌鸦,则有5只落在地上;如果每棵树上有5只乌鸦,则有一棵树上没有乌鸦,则共有 只乌鸦.
21.(2024春 玄武区校级月考)已知方程组的解是,则方程组的解为 .
22.(2024春 高新区校级月考)如果方程组和解的相同,则nm= .
23.(2024春 高新区校级月考)对于有理数x、y,定义新运算☆:x☆y=ax+by,其中a、b是常数.已知1☆2=1,(﹣3)☆3=6,则2☆(﹣5)的值是 .
24.(2024 高邮市二模)古代算书《四元玉鉴》中有“两果问价”问题:“甜果九个十一文钱,苦果七个四文钱,九百九十九文钱,甜果苦果买一千.试问甜苦果几个?”该问题意思是:已知十一文钱可买九个甜果,四文钱可买七个苦果,九百九十九文钱买了甜果和苦果共一千个,那么甜果、苦果各买了多少个?设甜果买了x个,苦果买了y个,根据题意,可列方程组是 .
25.(2024 宿迁模拟)科学研究表明:树叶在光合作用后产生的分泌物能够吸附空气中的悬浮颗粒物,具有滞尘净化空气的作用,已知一片银杏树叶一年的平均滞尘量比一片国槐树叶一年的平均滞尘量的2倍少4毫克,两片银杏树叶与三片国槐树叶一年的平均滞尘总量为146毫克.设一片银杏树叶一年的平均滞尘量为x毫克,一片国槐树叶一年的平均滞尘量为y毫克.依据题意,可列方程组为 .
26.(2024春 海陵区期末)若关于x,y的二元一次方程组的解为,则关于m,n二元一次方程组的解为 .
27.(2024春 江阴市月考)如图,这是一个计算机程序,规定从输入一个x值到判断结果是否≥15为一次运行过程,如果程序运行两次就停止,那么x的取值范围是 .
28.(2024春 东台市月考)若不等式组无解,则m的取值范围是 .
29.(2024春 玄武区校级月考)某商场促销方案规定:单笔消费金额每满100元立减10元.例如,单笔消费金额为208元时,立减20元.甲在该商场单笔购买2件A商品,立减了20元;乙在该商场单笔购买2件A商品与1件B商品,立减了30元.若B商品的单价是整数元,则它的最大值是 .
30.(2024秋 鼓楼区期末)已知三条不同的直线a,b,c在同一平面内,下列四个命题:
①如果a∥b,a⊥c,那么b⊥c; ②如果b∥a,c∥a,那么b∥c;
③如果b⊥a,c⊥a,那么b⊥c; ④如果b⊥a,c⊥a,那么b∥c.
其中正确的是 .(填写序号)
【江苏省各地区期末真题汇编】热点题型分类突破:填空题-2024-2024学年数学七年级下册苏科版(2024)
参考答案与试题解析
1.(2024春 宝应县期末)已知a=255,b=522,则a,b的大小关系是 b<a. (请用字母表示,并用“<”连接).
【解答】解:a=255=(25)11=3211,
b=522=(52)11=2511,
∵2511<3211,
∴522<255,
故答案为:b<a.
2.(2024春 赣榆区期末)已知ax=8,ay=32,则a2x﹣y的值为 2 .
【解答】解:∵ax=8,ay=32,
∴a2x﹣y=a2x÷ay=(ax)2÷ay=82÷32=2,
故答案为:2.
3.(2024春 锡山区校级月考)若m=2x+1,n=4x+2x,用含m的代数式表示n,则n= m2﹣m .
【解答】解:∵m=2x+1,
∴2x=m﹣1,
∴n=4x+2x
=(22)x+2x
=(2x)2+2x
=(m﹣1)2+m﹣1
=m2﹣2m+1+m﹣1
=m2﹣m,
故答案为:m2﹣m.
4.(2013春 崇安区校级期末)已知2m+3n=3,则4m 8n的值为 8 .
【解答】解:4m 8n=22m×23n=22m+3n,
∵2m+3n=3,
∴22m+3n=23=8.
故答案为8.
5.(2020春 洪泽区期末)计算x4÷x的结果等于 x3 .
【解答】解:x4÷x=x4﹣1=x3.
故答案为:x3.
6.(2024春 东台市月考)已知m+n=5,m﹣n=﹣1,则m2﹣n2= ﹣5 .
【解答】解:∵m+n=5,m﹣n=﹣1,
∴m2﹣n2=(m+n)(m﹣n)=5×(﹣1)=﹣5,
故答案为:﹣5.
7.(2024春 锡山区校级期末)如果代数式(mx﹣3)(x+2)的展开式不含x的一次项,那么m为 .
【解答】解:∵多项式(mx﹣3)(x+2)=mx2+(2m﹣3)x﹣6不含x的一次项,
∴2m﹣3=0,
解得m.
故答案为:.
8.(2024春 广陵区期末)若(x+p)(x﹣4)的展开式中不含有x项,则p= 4 .
【解答】解:∵多项式(x+p)(x﹣4)=x2+(p﹣4)x﹣4p不含x项,
∴p﹣4=0,
解得p=4.
故答案为:4.
9.(2024春 锡山区期末)如图,现有正方形卡片A类,B类和长方形卡片C类若干张,若要拼一个长为(2a+b),宽为(a+3b)的大长方形,则需C类卡片 7 张.
【解答】解:(2a+b)(a+3b)
=2a2+6ab+ab+3b2
=2a2+7ab+3b2,
根据题意得A类卡片的面积是a2,B类卡片的面积是b2,C类卡片的面积是ab,
所以需C类卡片7张,
故答案为:7.
10.(2024春 工业园区校级月考)计算:2024×2026﹣20242= ﹣1 .
【解答】解:2024×2026﹣20242
=(2024﹣1)(2024+1)﹣20242
=20242﹣1﹣20242
=﹣1.
11.(2024春 江阴市期末)设a=x﹣2023,b=x﹣2024,c=x﹣2024.若a2+b2=16,则c2的值是 7 .
【解答】解:由条件可知a﹣1=x﹣2024=c,b+1=x﹣2024=c,a﹣b=2,
∵(a﹣b)2=a2+b2﹣2ab,a2+b2=16,
∴22=16﹣2ab,则ab=6,
∴c2=(a﹣1)(b+1)
=ab+(a﹣b)﹣1
=6+2﹣1
=7,
故答案为:7.
12.(2024春 建邺区校级期末)若x2﹣5x﹣2=0,则(x﹣1)(x﹣2)(x﹣3)(x﹣4)= 48 .
【解答】解:∵x2﹣5x﹣2=0,
∴x2﹣5x=2,
∴(x﹣1)(x﹣2)(x﹣3)(x﹣4)
=[(x﹣1)(x﹣4)][(x﹣2)(x﹣3)]
=(x2﹣5x+4)(x2﹣5x+6)
=(2+4)×(2+6)
=6×8
=48,
故答案为:48.
13.(2024春 工业园区校级月考)如图,将△ABC沿BC方向平移3cm得到△DEF(其中点A,B,C分别与点D,E,F对应),若CE=6cm,则BF= 12 cm.
【解答】解:由题知,
因为△DEF由△ABC沿BC方向平移3cm得到,
所以BE=CF=3cm.
又因为CE=6cm,
所以BF=BE+CE+CF=3+6+3=12(cm).
故答案为:12.
14.(2024 梁溪区二模)如图,△ABC中,∠B=28°,将△ABC绕点A顺时针旋转52°得△AB′C′,AB′与BC交于D,则∠ADC= 80 °.
【解答】解:∵△ABC绕点A顺时针旋转52°得△AB′C′,
∴∠BAB′=52°,
∵∠B=28°,
∴∠ADB=180°﹣∠BAB′﹣∠B=100°,
∴∠ADC=180°﹣∠ADB=80°.
故答案为:80.
15.(2024春 广陵区期末)如图,在三角形纸片ABC中,∠ACB=36°,将三角形纸片ABC绕点C按逆时针方向旋转70°,得到三角形A′B′C,则∠BCA′的度数为 34° .
【解答】解:由题意知∠ACA′=70°,
∵∠ACB=36°,
∴∠BCA′=∠ACA′﹣∠ACB=34°,
故答案为:34°.
16.(2024秋 太仓市期末)如图,在△ABC中,AB的垂直平分线交BC于点D,交AB于点E,AC的垂直平分线交BC于点F,交AC于点G,连接AD,AF.若BC=6,BD=2,∠DAF=90°,则DF的长为 .
【解答】解:∵DE是AB的垂直平分线,BD=2,
∴AD=BD=2,
∵GF是AC的垂直平分线,
∴FA=FC,
∵BC=6,
∴FA=FC=4﹣DF,
∵∠DAF=90°,
∴DF2=AD2+AF2,即DF2=22+(4﹣DF)2,
解得:DF,
故答案为:.
17.(2024春 句容市期末)如图,将△ABC沿BC方向平移4cm得到△DEF,若BF=7CE,则BC的长为 3 cm.
【解答】解:由平移可得,BE=CF=AD=4cm,
∵BF=BE+EF=4+(CF﹣CE)=4+4﹣CE=7CE,
∴CE=1cm,
∴BC=BE﹣CE=4﹣1=3(cm),
故答案为:3.
18.(2024 淮阴区校级二模)已知是方程4x﹣6y﹣5=0的一个解,则2m﹣3n的值是 .
【解答】解:把代入方程4x﹣6y﹣5=0中,得4m﹣6n﹣5=0,
即2(2m﹣3n)=5,
∴2m﹣3n,
故答案为:.
19.(2024春 沛县月考)已知方程组和方程组的解相同,则a+b= 0 .
【解答】解:∵方程组和方程组的解相同,
联立得:,
①+②得:5x=10,即x=2,
把x=2代入①得:4+5y=﹣26,
解得:y=﹣6,
代入得:,
解得:a=1,b=﹣1,
则a+b=﹣1+1=0,
故答案为:0.
20.(2024 滨湖区二模)古代一歌谣:栖树一群鸦,鸦树不知数;三个坐一棵,五个地上落;五个坐一棵,闲了一棵树.意思是说,有一群乌鸦到树林休息,如果每棵树上有3只乌鸦,则有5只落在地上;如果每棵树上有5只乌鸦,则有一棵树上没有乌鸦,则共有 20 只乌鸦.
【解答】解:设乌鸦有x只,树有y棵,依题得
,
解得,
故答案为:20.
21.(2024春 玄武区校级月考)已知方程组的解是,则方程组的解为 .
【解答】解:∵的解是,
∴,
由①得:x=1,
由②得:y=4,
∴方程组的解为,
故答案为:.
22.(2024春 高新区校级月考)如果方程组和解的相同,则nm= 1 .
【解答】解:∵方程组和解的相同,
∴,
解得:,
∴2﹣m=2,2n﹣1=2,
解得:,
∴.
故答案为:1.
23.(2024春 高新区校级月考)对于有理数x、y,定义新运算☆:x☆y=ax+by,其中a、b是常数.已知1☆2=1,(﹣3)☆3=6,则2☆(﹣5)的值是 ﹣7 .
【解答】解:∵x☆y=ax+by,1☆2=1,(﹣3)☆3=6,
∴,
①×3得:3a+6b=3③,
②+③得:b=1,
把b=1代入①得:a=﹣1,
∴x☆y=﹣x+y,
∴2☆(﹣5)=﹣2﹣5=﹣7,
故答案为:﹣7.
24.(2024 高邮市二模)古代算书《四元玉鉴》中有“两果问价”问题:“甜果九个十一文钱,苦果七个四文钱,九百九十九文钱,甜果苦果买一千.试问甜苦果几个?”该问题意思是:已知十一文钱可买九个甜果,四文钱可买七个苦果,九百九十九文钱买了甜果和苦果共一千个,那么甜果、苦果各买了多少个?设甜果买了x个,苦果买了y个,根据题意,可列方程组是 .
【解答】解:∵买了甜果和苦果共一千个,
∴x+y=1000;
∵买甜果和苦果共花了999文钱,
∴xy=999,
∴根据题意可列方程组:,
故答案为:.
25.(2024 宿迁模拟)科学研究表明:树叶在光合作用后产生的分泌物能够吸附空气中的悬浮颗粒物,具有滞尘净化空气的作用,已知一片银杏树叶一年的平均滞尘量比一片国槐树叶一年的平均滞尘量的2倍少4毫克,两片银杏树叶与三片国槐树叶一年的平均滞尘总量为146毫克.设一片银杏树叶一年的平均滞尘量为x毫克,一片国槐树叶一年的平均滞尘量为y毫克.依据题意,可列方程组为 .
【解答】解:由题意得:.
故答案为:.
26.(2024春 海陵区期末)若关于x,y的二元一次方程组的解为,则关于m,n二元一次方程组的解为 .
【解答】解:设m+1=h,n﹣2=g,
可化为:,
则:可化为,
又∵的解为,
∴,
∴m+1=4,n﹣2=﹣2,
解得:m=3,n=0.
故答案为:.
27.(2024春 江阴市月考)如图,这是一个计算机程序,规定从输入一个x值到判断结果是否≥15为一次运行过程,如果程序运行两次就停止,那么x的取值范围是 x .
【解答】解:根据题意得:,
解得:x,
∴x的取值范围是x.
故答案为:x.
28.(2024春 东台市月考)若不等式组无解,则m的取值范围是 m≤2 .
【解答】解:,
解不等式2x﹣4>0,得x>2,
∴不等式组的解集为2<x<m,
∵不等式组无解,
∴m≤2,
故答案为:m≤2.
29.(2024春 玄武区校级月考)某商场促销方案规定:单笔消费金额每满100元立减10元.例如,单笔消费金额为208元时,立减20元.甲在该商场单笔购买2件A商品,立减了20元;乙在该商场单笔购买2件A商品与1件B商品,立减了30元.若B商品的单价是整数元,则它的最大值是 199 .
【解答】解:由题意可得,2件A产品的消费金额满足:200≤2件A产品的价格<300,
300≤2件A产品的价格+1件B产品的价格<400,
设B产品的单价为x元,
300≤200+x<400,
解得:100≤x<200,
∵B产品的单价为整数,
∴B商品的单价的最大值为199元.
故答案为:199.
30.(2024秋 鼓楼区期末)已知三条不同的直线a,b,c在同一平面内,下列四个命题:
①如果a∥b,a⊥c,那么b⊥c; ②如果b∥a,c∥a,那么b∥c;
③如果b⊥a,c⊥a,那么b⊥c; ④如果b⊥a,c⊥a,那么b∥c.
其中正确的是 ①②④ .(填写序号)
【解答】解:在同一个平面内,①如果a∥b,a⊥c,那么b⊥c;
②如果b∥a,c∥a,那么b∥c;
③如果b⊥a,c⊥a,那么b∥c;
④如果b⊥a,c⊥a,那么b∥c,
故答案为:①②④.
21世纪教育网 www.21cnjy.com 精品试卷·第 2 页 (共 2 页)
21世纪教育网(www.21cnjy.com)
同课章节目录
