【江苏省各地区期末真题汇编】热点题型分类突破:解答题(含解析)-2024-2025学年数学八年级下册苏科版
文档属性
| 名称 | 【江苏省各地区期末真题汇编】热点题型分类突破:解答题(含解析)-2024-2025学年数学八年级下册苏科版 |
|
|
| 格式 | docx | ||
| 文件大小 | 1.1MB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 苏科版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2025-05-30 00:00:00 | ||
图片预览



文档简介
中小学教育资源及组卷应用平台
【江苏省各地区期末真题汇编】热点题型分类突破:解答题-2024-2025学年数学八年级下册苏科版
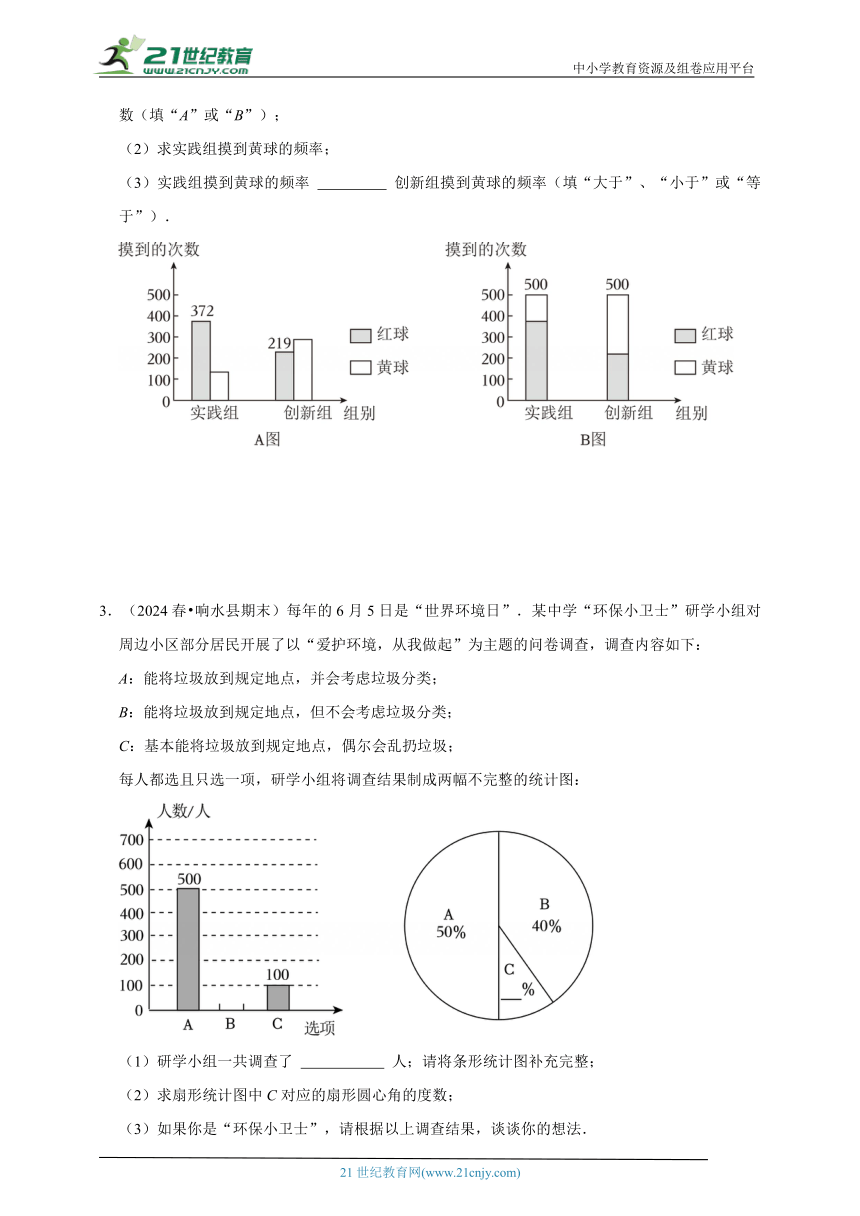
1.(2024秋 惠山区期末)为了解八年级学生每天完成课外作业时间的情况、从全区八年级学生中随机抽取了部分学生每天完成课外作业的时间进行调查,并将调查结果绘制成如下图表:
时间x(小时) 频数y(人数) 频率
0≤x≤0.5 8 0.2
0.5<x≤1 c 0.3
1<x≤1.5 12 0.3
1.5<x≤2 6 b
2<x≤2.5 2 0.05
合计 a 1
(1)表中a,b所表示的数分别为a= ,b= ;
(2)请在图中补全频数分布直方图;
(3)根据规定,学生每天完成课外作业的时间不超过1.5小时,那么全区4800名八年级学生中每天完成课外作业时间超过规定的学生约有多少人?
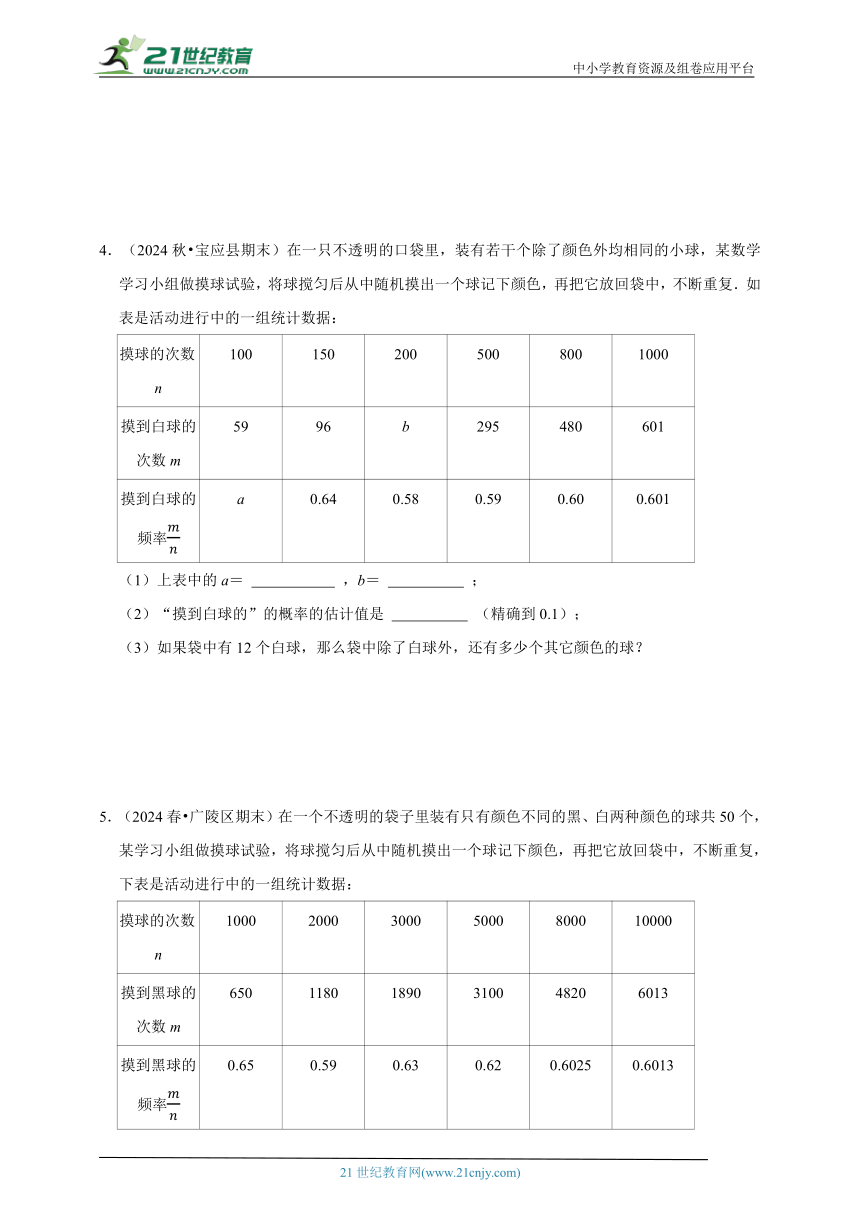
2.(2024秋 兴化市期末)有甲、乙两只不透明的袋子,每只袋子中装有红球和黄球若干,各袋中所装球的总个数相同,这些球除颜色外都相同.实践组用甲袋、创新组用乙袋各自做摸球试验:两人一组,一人从袋中任意摸出1个球,另一人记下颜色后将球放回并搅匀,各组连续做这样的试验,将记录的数据绘制成如下两种条形统计图:
(1) 图能更好地反各组试验的总次数, 图能更好地反映各组试验摸到红球的频数(填“A”或“B”);
(2)求实践组摸到黄球的频率;
(3)实践组摸到黄球的频率 创新组摸到黄球的频率(填“大于”、“小于”或“等于”).
3.(2024春 响水县期末)每年的6月5日是“世界环境日”.某中学“环保小卫士”研学小组对周边小区部分居民开展了以“爱护环境,从我做起”为主题的问卷调查,调查内容如下:
A:能将垃圾放到规定地点,并会考虑垃圾分类;
B:能将垃圾放到规定地点,但不会考虑垃圾分类;
C:基本能将垃圾放到规定地点,偶尔会乱扔垃圾;
每人都选且只选一项,研学小组将调查结果制成两幅不完整的统计图:
(1)研学小组一共调查了 人;请将条形统计图补充完整;
(2)求扇形统计图中C对应的扇形圆心角的度数;
(3)如果你是“环保小卫士”,请根据以上调查结果,谈谈你的想法.
4.(2024秋 宝应县期末)在一只不透明的口袋里,装有若干个除了颜色外均相同的小球,某数学学习小组做摸球试验,将球搅匀后从中随机摸出一个球记下颜色,再把它放回袋中,不断重复.如表是活动进行中的一组统计数据:
摸球的次数n 100 150 200 500 800 1000
摸到白球的次数m 59 96 b 295 480 601
摸到白球的频率 a 0.64 0.58 0.59 0.60 0.601
(1)上表中的a= ,b= ;
(2)“摸到白球的”的概率的估计值是 (精确到0.1);
(3)如果袋中有12个白球,那么袋中除了白球外,还有多少个其它颜色的球?
5.(2024春 广陵区期末)在一个不透明的袋子里装有只有颜色不同的黑、白两种颜色的球共50个,某学习小组做摸球试验,将球搅匀后从中随机摸出一个球记下颜色,再把它放回袋中,不断重复,下表是活动进行中的一组统计数据:
摸球的次数n 1000 2000 3000 5000 8000 10000
摸到黑球的次数m 650 1180 1890 3100 4820 6013
摸到黑球的频率 0.65 0.59 0.63 0.62 0.6025 0.6013
(1)请估计:当n很大时,摸到黑球的频率将会接近 (精确到0.1);
(2)试估计袋子中有黑球 个;
(3)若学习小组通过试验结果,想使得在这个不透明袋子中每次摸到黑球的可能性大小为50%,则可以在袋子中增加相同的白球 个或减少黑球 个.
6.(2024春 姑苏区期末)如图,在△ABC中,∠BAC=90°,AD是斜边上的中线,E是AD的中点,过点A作AF∥BC交BE的延长线于F,连接CF.
(1)求证:BD=AF;
(2)判断四边形ADCF的形状,并证明你的结论.
7.(2023春 玄武区期末)如图,在△ABC中,∠ACB=90°,D、E分别是AB、AC的中点,过点C作CF∥AB,交DE延长线于点F,连接AF、CD.
(1)求证:四边形ADCF是菱形;
(2)当 时,四边形ADCF是正方形.
8.(2024春 邗江区期末)如图,在 ABCD中,∠ABD的平分线BE交AD于点E,∠CDB的平分线DF交BC于点F.
(1)求证:△ABE≌△CDF;
(2)若AB=DB,求证:四边形DFBE是矩形.
9.(2023春 亭湖区校级期末)如图, ABCD对角线AC,BD相交于点O,过点D作DE∥AC且DE=OC,连接CE,OE,OE=CD.
(1)求证: ABCD是菱形;
(2)若AB=4,∠ABC=60°,求AE的长.
10.(2024秋 如东县期末)【追本溯源】题(1)来自于课本中的习题,请你完成解答,提炼方法并完成题(2).
(1)如图1,AD∥BC,BD平分∠ABC.求证:AB=AD.
【方法应用】
(2)如图2,AD∥BC,AB∥DC,BE平分∠ABC,交边AD于点E,过点A作AF⊥BE交DC的延长线于点F.若AD=6,CD=3.5,求CF的长.
11.(2021春 广陵区校级期末)随着人们“节能环保,绿色出行”意识的增强,越来越多的人喜欢骑自行车出行,也给自行车商家带来商机.某自行车行经营的A型自行车去年销售总额为8万元.今年该型自行车每辆售价预计比去年降低200元.若该型车的销售数量与去年相同,那么今年的销售总额将比去年减少10%,求:A型自行车去年每辆售价多少元?
12.(2024秋 宿城区校级期末)对于一些特殊的方程,我们给出两个定义:①若两个方程有相同的解,则称这两个方程为“相似方程”;②若两个方程有相同的整数解,则称这两个方程为“相伴方程”.
(1)判断方程6﹣4(1﹣x)=2x与是否为“相似方程”,并说明理由;
(2)已知关于x,y的二元一次方程y=mx+6和y=x+4m是“相伴方程”,求正整数m的值.
13.(2022秋 海安市期末)阅读材料:对于非零实数a,b,若关于x的分式的值为零,则解得x1=a,x2=b.又因为x(a+b),所以关于x的方程x(a+b),的解为x1=a,x2=b.
(1)理解应用:方程3的解为:x1= ,x2= ;
(2)知识迁移:若关于x的方程x5的解为x1=a,x2=b,求a2+b2的值;
(3)拓展提升:若关于x的方程k﹣x的解为x1,x2,且x1x2=1,求k的值.
14.(2024春 姑苏区期末)如图,一次函数y=kx+b的图象与反比例函数的图象交于A(1,6),B(3,n)两点,与x轴交于点C.
(1)求一次函数与反比例函数的表达式;
(2)连接OA,OB,求△AOB的面积.
15.(2022春 宿迁期末)如图,一次函数y1=ax+b与反比例函数y2的图象相交于A(2,8),B(8,2)两点,连接AO,BO,延长AO交反比例函数图象于点C.
(1)求一次函数y1的表达式与反比例函数y2的表达式;
(2)当y1<y2,时,直接写出自变量x的取值范围为 ;
(3)点P是x轴上一点,当S△PACS△AOB时,请直接写出点P的坐标为 .
16.(2024春 连云港期末)心理学研究发现,一般情况下,在一节45分钟的课中,学生的注意力随学习时间的变化而变化.开始学习时,学生的注意力逐步增强,中间有一段时间学生的注意力保持较为理想的稳定状态,随后学生的注意力开始分散.经过实验分析可知,学生的注意力指标数y随时间x(分钟)的变化规律如图所示(其中AB、BC分别为线段,CD为双曲线的一部分).
(1)开始学习后第5分钟时与第35分钟时相比较,何时学生的注意力更集中?为什么?
(2)某些数学内容的课堂学习大致可分为三个环节:即“教师引导,回顾旧知﹣﹣自主探索,合作交流﹣﹣总结归纳,巩固提高”.其中重点环节“自主探索,合作交流”这一过程一般需要30分钟才能完成,为了确保效果,要求学习时的注意力指标数不低于40.请问这样的课堂学习安排是否合理?并说明理由.
17.(2024春 泗阳县期末)已知反比例函数y(k常数,k≠2).
(1)若点A(1,2)在这个函数的图象上,求k的值;
(2)若这个函数图象的每一支上,y都随x的增大而增大,求k的取值范围;
(3)若k=8,试写出当﹣3≤y≤﹣2时x的取值范围.
18.(2022春 淮阴区期末)如图,在平面直角坐标系中,直线y1=k1x+b与双曲线y2相交于A(﹣2,3),B(m,﹣2)两点.
(1)求y1、y2对应的函数表达式;
(2)过点B作BP∥x轴交y轴于点P,求△ABP的面积.
19.(2024秋 邗江区校级期末)我们在学习二次根式的时候会发现:有时候两个含有二次根式的代数式相乘,积不含有二次根式,如,.课本中阅读材料告诉我们,两个含有二次根式的非零代数式相乘,如果它们的积不是二次根式,那么这两个代数式互为有理化因式.
请运用有理化因式的知识,解决下列问题:
(1)化简: ;
(2)比较大小: ;(用“>”、“=”或“<”填空)
(3)设有理数a、b满足:,则a+b= ;
(4)已知,求的值.
20.(2023秋 沭阳县校级期末)定义:若一个三角形存在两边平方和等于第三边平方的3倍,则称此三角形为“平方倍三角形”.
(1)若一个三角形的三边长分别是,和2,这个三角形是否为平方倍三角形?请你作出判断并说明理由.
(2)若一个直角三角形是平方倍三角形,求该直角三角形的三边之比(结果按从小到大的顺序排列).
【江苏省各地区期末真题汇编】热点题型分类突破:解答题-2024-2025学年数学八年级下册苏科版
参考答案与试题解析
一.解答题(共20小题)
1.(2024秋 惠山区期末)为了解八年级学生每天完成课外作业时间的情况、从全区八年级学生中随机抽取了部分学生每天完成课外作业的时间进行调查,并将调查结果绘制成如下图表:
时间x(小时) 频数y(人数) 频率
0≤x≤0.5 8 0.2
0.5<x≤1 c 0.3
1<x≤1.5 12 0.3
1.5<x≤2 6 b
2<x≤2.5 2 0.05
合计 a 1
(1)表中a,b所表示的数分别为a= 40 ,b= 0.15 ;
(2)请在图中补全频数分布直方图;
(3)根据规定,学生每天完成课外作业的时间不超过1.5小时,那么全区4800名八年级学生中每天完成课外作业时间超过规定的学生约有多少人?
【解答】解:(1)a=8÷0.2=40,b=6÷40=0.15,
故答案为:40、0.15;
(2)c=0.3×40=12,补全图形如下:
(3)4800×(0.15+0.05)=960(人),
答:全区4800名八年级学生中每天完成课外作业时间超过规定的学生约有960人.
2.(2024秋 兴化市期末)有甲、乙两只不透明的袋子,每只袋子中装有红球和黄球若干,各袋中所装球的总个数相同,这些球除颜色外都相同.实践组用甲袋、创新组用乙袋各自做摸球试验:两人一组,一人从袋中任意摸出1个球,另一人记下颜色后将球放回并搅匀,各组连续做这样的试验,将记录的数据绘制成如下两种条形统计图:
(1) B 图能更好地反各组试验的总次数, A 图能更好地反映各组试验摸到红球的频数(填“A”或“B”);
(2)求实践组摸到黄球的频率;
(3)实践组摸到黄球的频率 小于 创新组摸到黄球的频率(填“大于”、“小于”或“等于”).
【解答】解:(1)B图能更好地反映各组试验的总次数,A图能更好地反映各组试验摸到红球的频数;
故答案为:B,A.
(2)实践组摸到黄球的频率=(500﹣372)÷500=0.256;
(3)实践组摸到黄球的频率小于创新组摸到黄球的频率(答案不唯一).
3.(2024春 响水县期末)每年的6月5日是“世界环境日”.某中学“环保小卫士”研学小组对周边小区部分居民开展了以“爱护环境,从我做起”为主题的问卷调查,调查内容如下:
A:能将垃圾放到规定地点,并会考虑垃圾分类;
B:能将垃圾放到规定地点,但不会考虑垃圾分类;
C:基本能将垃圾放到规定地点,偶尔会乱扔垃圾;
每人都选且只选一项,研学小组将调查结果制成两幅不完整的统计图:
(1)研学小组一共调查了 1000 人;请将条形统计图补充完整;
(2)求扇形统计图中C对应的扇形圆心角的度数;
(3)如果你是“环保小卫士”,请根据以上调查结果,谈谈你的想法.
【解答】解:(1)500÷50%=1000(人),
所以研学小组一共调查了1000人;
B处理方式的人数为:1000﹣500﹣100=400(人),
补全条形统计图,如图所示:
(2)C处理方式的百分比为:100%﹣50%﹣40%=10%,
扇形统计图中C对应的扇形圆心角的度数为:360°×10%=36°.
(3)将垃圾放到规定地点,并分类放置,保护环境,从自身做起.(答案不唯一)
4.(2024秋 宝应县期末)在一只不透明的口袋里,装有若干个除了颜色外均相同的小球,某数学学习小组做摸球试验,将球搅匀后从中随机摸出一个球记下颜色,再把它放回袋中,不断重复.如表是活动进行中的一组统计数据:
摸球的次数n 100 150 200 500 800 1000
摸到白球的次数m 59 96 b 295 480 601
摸到白球的频率 a 0.64 0.58 0.59 0.60 0.601
(1)上表中的a= 0.59 ,b= 116 ;
(2)“摸到白球的”的概率的估计值是 0.6 (精确到0.1);
(3)如果袋中有12个白球,那么袋中除了白球外,还有多少个其它颜色的球?
【解答】解:(1)a=59÷100=0.59,b=200×0.58=116.
故答案为:0.59,116
(2)“摸到白球的”的概率的估计值是0.6;
故答案为:0.6
(3)12÷0.6﹣12=8(个).
答:除白球外,还有大约8个其它颜色的小球;
5.(2024春 广陵区期末)在一个不透明的袋子里装有只有颜色不同的黑、白两种颜色的球共50个,某学习小组做摸球试验,将球搅匀后从中随机摸出一个球记下颜色,再把它放回袋中,不断重复,下表是活动进行中的一组统计数据:
摸球的次数n 1000 2000 3000 5000 8000 10000
摸到黑球的次数m 650 1180 1890 3100 4820 6013
摸到黑球的频率 0.65 0.59 0.63 0.62 0.6025 0.6013
(1)请估计:当n很大时,摸到黑球的频率将会接近 0.6 (精确到0.1);
(2)试估计袋子中有黑球 30 个;
(3)若学习小组通过试验结果,想使得在这个不透明袋子中每次摸到黑球的可能性大小为50%,则可以在袋子中增加相同的白球 10 个或减少黑球 10 个.
【解答】解:(1)观察表格得:当n很大时,摸到黑球的频率将会接近0.6,
故答案为:0.6;
(2)黑球的个数为50×0.6=30个,
故答案为:30;
(3)想使得在这个不透明袋子中每次摸到黑球的可能性大小为50%,则可以使得黑球和白球的个数相同,
即:在袋子中增加相同的白球10个或减少黑球10个,
故答案为:10,10.
6.(2024春 姑苏区期末)如图,在△ABC中,∠BAC=90°,AD是斜边上的中线,E是AD的中点,过点A作AF∥BC交BE的延长线于F,连接CF.
(1)求证:BD=AF;
(2)判断四边形ADCF的形状,并证明你的结论.
【解答】(1)证明:∵AF∥BC,
∴∠AFE=∠DBE,
∵E是AD的中点,AD是BC边上的中线,
∴AE=DE,BD=CD,
在△AFE和△DBE中,,
∴△AFE≌△DBE(AAS),
∴BD=AF;
(2)解:四边形ADCF是菱形;理由如下:
由(1)知,AF=DB.
∵DB=DC,
∴AF=CD.
∵AF∥BC,
∴四边形ADCF是平行四边形,
∵∠BAC=90°,D是BC的中点,
∴AD=DCBC,
∴四边形ADCF是菱形.
7.(2023春 玄武区期末)如图,在△ABC中,∠ACB=90°,D、E分别是AB、AC的中点,过点C作CF∥AB,交DE延长线于点F,连接AF、CD.
(1)求证:四边形ADCF是菱形;
(2)当 时,四边形ADCF是正方形.
【解答】(1)证明:∵D、E分别是AB、AC中点,
∴DE是△ABC的中位线,
∴DE∥BC,
又∵CF∥AB,
∴四边形DBCF是平行四边形,
∴CF=BD,
∵D是AB的中点,
∴AD=BD,
∴CF=AD,
又∵CF∥AB,
∴四边形ADCF是平行四边形,
∵∠ACB=90°,D是AB中点,
∴.
∴CD=AD.
又∵四边形ADCF是平行四边形,
∴四边形ADCF是菱形;
(2)解:当时,四边形ADCF是正方形.
∵∠ACB=90°,
∴设ABk,AC=k,
∴BCk,
∴AC=BC,
∴△ABC是等腰直角三角形,
∵D是AB的中点,
∴CD⊥AB,
∴∠ADC=90°,
由(1)知,四边形ADCF是菱形,
∴四边形ADCF是正方形.
故答案为:.
8.(2024春 邗江区期末)如图,在 ABCD中,∠ABD的平分线BE交AD于点E,∠CDB的平分线DF交BC于点F.
(1)求证:△ABE≌△CDF;
(2)若AB=DB,求证:四边形DFBE是矩形.
【解答】证明:(1)∵∠ABD的平分线BE交AD于点E,
∴∠ABE∠ABD,
∵∠CDB的平分线DF交BC于点F,
∴∠CDF∠CDB,
∵在平行四边形ABCD中,
∴AB∥CD,
∴∠ABD=∠CDB,
∴∠CDF=∠ABE,
∵四边形ABCD是平行四边形,
∴CD=AB,∠A=∠C,
即,
∴△ABE≌△CDF(ASA);
(2)∵△ABE≌△CDF,
∴AE=CF,
∵四边形ABCD是平行四边形,
∴AD∥BC,AD=BC,
∴DE∥BF,DE=BF,
∴四边形DFBE是平行四边形,
∵AB=DB,BE平分∠ABD,
∴BE⊥AD,即∠DEB=90°.
∴平行四边形DFBE是矩形.
9.(2023春 亭湖区校级期末)如图, ABCD对角线AC,BD相交于点O,过点D作DE∥AC且DE=OC,连接CE,OE,OE=CD.
(1)求证: ABCD是菱形;
(2)若AB=4,∠ABC=60°,求AE的长.
【解答】(1)证明:∵DE∥AC,DE=OC,
∴四边形OCED是平行四边形.
∵OE=CD,
∴平行四边形OCED是矩形,
∴∠COD=90°,
∴AC⊥BD,
∴ ABCD是菱形;
(2)解:∵四边形ABCD是菱形,
∴OA=OC,CD=AB=BC=4,AC⊥BD,
∵∠ABC=60°,
∴△ABC是等边三角形,
∴AC=AB=4,
∴OA=OC=2,
在Rt△OCD中,由勾股定理得:OD2,
由(1)可知,四边形OCED是矩形,
∴CE=OD=2,∠OCE=90°,
∴AE2,
即AE的长为2.
10.(2024秋 如东县期末)【追本溯源】题(1)来自于课本中的习题,请你完成解答,提炼方法并完成题(2).
(1)如图1,AD∥BC,BD平分∠ABC.求证:AB=AD.
【方法应用】
(2)如图2,AD∥BC,AB∥DC,BE平分∠ABC,交边AD于点E,过点A作AF⊥BE交DC的延长线于点F.若AD=6,CD=3.5,求CF的长.
【解答】(1)证明:∵BD平分∠ABC,
∴∠ABD=∠CBD.
∵AD∥BC,
∴∠ADB=∠CBD,
∴∠ADB=∠ABD,
∴AB=AD;
(2)解:∵AD∥BC,AB∥CD,
∴四边形ABCD是平行四边形,∠BAF=∠F,
∴BC=AD=6,AB=CD=3.5,
由(1)可知,∠ABE=∠EBG=∠AEB,AB=AE,
∵AF⊥BE,
∴∠BAF=∠EAF,
∴∠EAF=∠F,
∴DF=AD=6,
∴CF=DF﹣CD=6﹣3.5=2.5.
11.(2021春 广陵区校级期末)随着人们“节能环保,绿色出行”意识的增强,越来越多的人喜欢骑自行车出行,也给自行车商家带来商机.某自行车行经营的A型自行车去年销售总额为8万元.今年该型自行车每辆售价预计比去年降低200元.若该型车的销售数量与去年相同,那么今年的销售总额将比去年减少10%,求:A型自行车去年每辆售价多少元?
【解答】解:设去年A型车每辆售价x元,则今年售价每辆为(x﹣200)元,
由题意,得,
解得:x=2000.
经检验,x=2000是原方程的根.
答:去年A型车每辆售价为2000元.
12.(2024秋 宿城区校级期末)对于一些特殊的方程,我们给出两个定义:①若两个方程有相同的解,则称这两个方程为“相似方程”;②若两个方程有相同的整数解,则称这两个方程为“相伴方程”.
(1)判断方程6﹣4(1﹣x)=2x与是否为“相似方程”,并说明理由;
(2)已知关于x,y的二元一次方程y=mx+6和y=x+4m是“相伴方程”,求正整数m的值.
【解答】解:(1)方程6﹣4(1﹣x)=2x与方程是“相似方程”,理由如下:
解方程6﹣4(1﹣x)=2x得:x=﹣1,
解方程得:x=﹣1,
检验:x=﹣1是该分式方程得解.
∴两个方程是“相似方程”;
(2)由条件可知mx+6=x+4m,
,
∵x,y,m均为整数,
∴m﹣1=±1,m﹣1=±2,
∴m1=0,m2=2,m3=﹣1,m4=3,
又∵m为正整数,
∴m=2或m=3.
13.(2022秋 海安市期末)阅读材料:对于非零实数a,b,若关于x的分式的值为零,则解得x1=a,x2=b.又因为x(a+b),所以关于x的方程x(a+b),的解为x1=a,x2=b.
(1)理解应用:方程3的解为:x1= 3 ,x2= ;
(2)知识迁移:若关于x的方程x5的解为x1=a,x2=b,求a2+b2的值;
(3)拓展提升:若关于x的方程k﹣x的解为x1,x2,且x1x2=1,求k的值.
【解答】解:(1)∵xa+b的解为x1=a,x2=b,
∴的解为x=3或x,
故答案为:3,;
(2)∵x5,
∴a+b=5,ab=3,
∴a2+b2=(a+b)2﹣2ab=25﹣6=19;
(3)k﹣x可化为x2﹣(k+1)x+4+k=0,
∵x1x2=1,
∴4+k=1,
∴k=﹣3.
14.(2024春 姑苏区期末)如图,一次函数y=kx+b的图象与反比例函数的图象交于A(1,6),B(3,n)两点,与x轴交于点C.
(1)求一次函数与反比例函数的表达式;
(2)连接OA,OB,求△AOB的面积.
【解答】解:(1)∵一次函数y=kx+b的图象与反比例函数y(x>0)的图象交于A(1,6),B(3,n)两点,
∴m=6×1=3×n,
∴m=6,n=2,
∵,
解得:,
∴一次函数解析式y=﹣2x+8,
反比例函数的解析式y.
(2)∵一次函数解析式y=﹣2x+8图象交x轴为点C,
∴C(4,0),
∵△AOB面积=△AOC面积﹣△COB面积4×64×2=12﹣4=8.
15.(2022春 宿迁期末)如图,一次函数y1=ax+b与反比例函数y2的图象相交于A(2,8),B(8,2)两点,连接AO,BO,延长AO交反比例函数图象于点C.
(1)求一次函数y1的表达式与反比例函数y2的表达式;
(2)当y1<y2,时,直接写出自变量x的取值范围为 x>8或0<x<2 ;
(3)点P是x轴上一点,当S△PACS△AOB时,请直接写出点P的坐标为 P(3,0)或P(﹣3,0) .
【解答】解:(1)将A(2,8),B(8,2)代入y1=ax+b得,
解得,
∴一次函数为y1=﹣x+10,
将A(2,8)代入y2得8,解得k=16,
∴反比例函数的解析式为y2;
(2)由图象可知,当y1<y2时,自变量x的取值范围为:x>8或0<x<2,
故答案为x>8或0<x<2;
(3)由题意可知OA=OC,
∴S△APC=2S△AOP,
把y=0代入y1=﹣x+10得,0=﹣x+10,解得x=10,
∴D(10,0),
∴S△AOB=S△AOD﹣S△BOD30,
∵S△PACS△AOB30=24,
∴2S△AOP=24,
∴2yA=24,即2OP×8=24,
∴OP=3,
∴P(3,0)或P(﹣3,0),
故答案为P(3,0)或P(﹣3,0).
16.(2024春 连云港期末)心理学研究发现,一般情况下,在一节45分钟的课中,学生的注意力随学习时间的变化而变化.开始学习时,学生的注意力逐步增强,中间有一段时间学生的注意力保持较为理想的稳定状态,随后学生的注意力开始分散.经过实验分析可知,学生的注意力指标数y随时间x(分钟)的变化规律如图所示(其中AB、BC分别为线段,CD为双曲线的一部分).
(1)开始学习后第5分钟时与第35分钟时相比较,何时学生的注意力更集中?为什么?
(2)某些数学内容的课堂学习大致可分为三个环节:即“教师引导,回顾旧知﹣﹣自主探索,合作交流﹣﹣总结归纳,巩固提高”.其中重点环节“自主探索,合作交流”这一过程一般需要30分钟才能完成,为了确保效果,要求学习时的注意力指标数不低于40.请问这样的课堂学习安排是否合理?并说明理由.
【解答】解:(1)设yAB=k1x+b,把(0,20),(10,50)代入函数解析式解得yAB=3x+20(0≤x≤10),
由图象直接得到yBC=50(10≤x≤30),
设yCD,把(30,50)代入函数解析式解得yCD(30≤x≤45);
把x=5代入yAB=3x+20,得yAB=35,
把x=35代入yCD,得yCD,
因为yAB≤yCD,
所以第35分钟时学生的注意力更集中;
(2)由题意知,注意力指数不低于40
即当在3x+20≥40,x
同时40
即x37.5
即当开始上课分钟直至上课37.5分钟时学生的注意力指数均不小于40.
而37.530,
∴该学习设计合理.
17.(2024春 泗阳县期末)已知反比例函数y(k常数,k≠2).
(1)若点A(1,2)在这个函数的图象上,求k的值;
(2)若这个函数图象的每一支上,y都随x的增大而增大,求k的取值范围;
(3)若k=8,试写出当﹣3≤y≤﹣2时x的取值范围.
【解答】解:(1)把点A(1,2)代入反比例函数y得:k﹣2=1×2,
∴k=4
因此k的值为:4;
(2)反比例函数y每一支上,y都随x的增大而增大,
∴k﹣2<0,
∴k<2;
(3)当k=8时,反比例函数的关系式为y,此时在每个象限内,y随x的增大而减小,
当y=﹣3时,x=﹣2,
当y=﹣2时,x=﹣3,
∴x的取值范围为:﹣3≤x≤﹣2.
18.(2022春 淮阴区期末)如图,在平面直角坐标系中,直线y1=k1x+b与双曲线y2相交于A(﹣2,3),B(m,﹣2)两点.
(1)求y1、y2对应的函数表达式;
(2)过点B作BP∥x轴交y轴于点P,求△ABP的面积.
【解答】解:(1)∵直线y1=k1x+b与双曲线y2相交于A(﹣2,3),B(m,﹣2)两点,
∴k2=﹣2×3=﹣2m
∴k2=﹣6,m=3,
∴双曲线的表达式为:y2,B(3,﹣2),
把A(﹣2,3)和B(3,﹣2)代入y1=k1x+b得:,
解得:,
∴直线的表达式为:y1=﹣x+1;
(2)∵BP∥x轴,B(3,﹣2),
∴BP=3,
∴S△ABP.
19.(2024秋 邗江区校级期末)我们在学习二次根式的时候会发现:有时候两个含有二次根式的代数式相乘,积不含有二次根式,如,.课本中阅读材料告诉我们,两个含有二次根式的非零代数式相乘,如果它们的积不是二次根式,那么这两个代数式互为有理化因式.
请运用有理化因式的知识,解决下列问题:
(1)化简: ;
(2)比较大小: < ;(用“>”、“=”或“<”填空)
(3)设有理数a、b满足:,则a+b= ﹣6 ;
(4)已知,求的值.
【解答】解:(1)原式.
故答案为:;
(2)∵,,
∵,
∴;
故答案为:<;
(3)∵,
∴(1)a+(1)b=﹣64,
∴(a+b)a+b=﹣64,
∵a,b是有理数,
∴a+b=﹣6,﹣a+b=4.
故答案为:﹣6;
(4)∵,
∴,
∴,
∴3.
20.(2023秋 沭阳县校级期末)定义:若一个三角形存在两边平方和等于第三边平方的3倍,则称此三角形为“平方倍三角形”.
(1)若一个三角形的三边长分别是,和2,这个三角形是否为平方倍三角形?请你作出判断并说明理由.
(2)若一个直角三角形是平方倍三角形,求该直角三角形的三边之比(结果按从小到大的顺序排列).
【解答】解:(1)结论:这个三角形是“平方倍三角形”.理由如下:
∵()2+22=15,3×()2=15,
∴()2+22=3×()2,
∴这个三角形是“平方倍三角形”.
(2)设两直角边长为:a,b,斜边长为:c,
∵△ABC为“平方倍三角形”.
∴a2+b2=c2,且c2+a2=3b2,
∴2a2+b2=3b2,
∴b=a,
∴ca,
∴a:b:c=1:1:.
21世纪教育网 www.21cnjy.com 精品试卷·第 2 页 (共 2 页)
21世纪教育网(www.21cnjy.com)
【江苏省各地区期末真题汇编】热点题型分类突破:解答题-2024-2025学年数学八年级下册苏科版
1.(2024秋 惠山区期末)为了解八年级学生每天完成课外作业时间的情况、从全区八年级学生中随机抽取了部分学生每天完成课外作业的时间进行调查,并将调查结果绘制成如下图表:
时间x(小时) 频数y(人数) 频率
0≤x≤0.5 8 0.2
0.5<x≤1 c 0.3
1<x≤1.5 12 0.3
1.5<x≤2 6 b
2<x≤2.5 2 0.05
合计 a 1
(1)表中a,b所表示的数分别为a= ,b= ;
(2)请在图中补全频数分布直方图;
(3)根据规定,学生每天完成课外作业的时间不超过1.5小时,那么全区4800名八年级学生中每天完成课外作业时间超过规定的学生约有多少人?
2.(2024秋 兴化市期末)有甲、乙两只不透明的袋子,每只袋子中装有红球和黄球若干,各袋中所装球的总个数相同,这些球除颜色外都相同.实践组用甲袋、创新组用乙袋各自做摸球试验:两人一组,一人从袋中任意摸出1个球,另一人记下颜色后将球放回并搅匀,各组连续做这样的试验,将记录的数据绘制成如下两种条形统计图:
(1) 图能更好地反各组试验的总次数, 图能更好地反映各组试验摸到红球的频数(填“A”或“B”);
(2)求实践组摸到黄球的频率;
(3)实践组摸到黄球的频率 创新组摸到黄球的频率(填“大于”、“小于”或“等于”).
3.(2024春 响水县期末)每年的6月5日是“世界环境日”.某中学“环保小卫士”研学小组对周边小区部分居民开展了以“爱护环境,从我做起”为主题的问卷调查,调查内容如下:
A:能将垃圾放到规定地点,并会考虑垃圾分类;
B:能将垃圾放到规定地点,但不会考虑垃圾分类;
C:基本能将垃圾放到规定地点,偶尔会乱扔垃圾;
每人都选且只选一项,研学小组将调查结果制成两幅不完整的统计图:
(1)研学小组一共调查了 人;请将条形统计图补充完整;
(2)求扇形统计图中C对应的扇形圆心角的度数;
(3)如果你是“环保小卫士”,请根据以上调查结果,谈谈你的想法.
4.(2024秋 宝应县期末)在一只不透明的口袋里,装有若干个除了颜色外均相同的小球,某数学学习小组做摸球试验,将球搅匀后从中随机摸出一个球记下颜色,再把它放回袋中,不断重复.如表是活动进行中的一组统计数据:
摸球的次数n 100 150 200 500 800 1000
摸到白球的次数m 59 96 b 295 480 601
摸到白球的频率 a 0.64 0.58 0.59 0.60 0.601
(1)上表中的a= ,b= ;
(2)“摸到白球的”的概率的估计值是 (精确到0.1);
(3)如果袋中有12个白球,那么袋中除了白球外,还有多少个其它颜色的球?
5.(2024春 广陵区期末)在一个不透明的袋子里装有只有颜色不同的黑、白两种颜色的球共50个,某学习小组做摸球试验,将球搅匀后从中随机摸出一个球记下颜色,再把它放回袋中,不断重复,下表是活动进行中的一组统计数据:
摸球的次数n 1000 2000 3000 5000 8000 10000
摸到黑球的次数m 650 1180 1890 3100 4820 6013
摸到黑球的频率 0.65 0.59 0.63 0.62 0.6025 0.6013
(1)请估计:当n很大时,摸到黑球的频率将会接近 (精确到0.1);
(2)试估计袋子中有黑球 个;
(3)若学习小组通过试验结果,想使得在这个不透明袋子中每次摸到黑球的可能性大小为50%,则可以在袋子中增加相同的白球 个或减少黑球 个.
6.(2024春 姑苏区期末)如图,在△ABC中,∠BAC=90°,AD是斜边上的中线,E是AD的中点,过点A作AF∥BC交BE的延长线于F,连接CF.
(1)求证:BD=AF;
(2)判断四边形ADCF的形状,并证明你的结论.
7.(2023春 玄武区期末)如图,在△ABC中,∠ACB=90°,D、E分别是AB、AC的中点,过点C作CF∥AB,交DE延长线于点F,连接AF、CD.
(1)求证:四边形ADCF是菱形;
(2)当 时,四边形ADCF是正方形.
8.(2024春 邗江区期末)如图,在 ABCD中,∠ABD的平分线BE交AD于点E,∠CDB的平分线DF交BC于点F.
(1)求证:△ABE≌△CDF;
(2)若AB=DB,求证:四边形DFBE是矩形.
9.(2023春 亭湖区校级期末)如图, ABCD对角线AC,BD相交于点O,过点D作DE∥AC且DE=OC,连接CE,OE,OE=CD.
(1)求证: ABCD是菱形;
(2)若AB=4,∠ABC=60°,求AE的长.
10.(2024秋 如东县期末)【追本溯源】题(1)来自于课本中的习题,请你完成解答,提炼方法并完成题(2).
(1)如图1,AD∥BC,BD平分∠ABC.求证:AB=AD.
【方法应用】
(2)如图2,AD∥BC,AB∥DC,BE平分∠ABC,交边AD于点E,过点A作AF⊥BE交DC的延长线于点F.若AD=6,CD=3.5,求CF的长.
11.(2021春 广陵区校级期末)随着人们“节能环保,绿色出行”意识的增强,越来越多的人喜欢骑自行车出行,也给自行车商家带来商机.某自行车行经营的A型自行车去年销售总额为8万元.今年该型自行车每辆售价预计比去年降低200元.若该型车的销售数量与去年相同,那么今年的销售总额将比去年减少10%,求:A型自行车去年每辆售价多少元?
12.(2024秋 宿城区校级期末)对于一些特殊的方程,我们给出两个定义:①若两个方程有相同的解,则称这两个方程为“相似方程”;②若两个方程有相同的整数解,则称这两个方程为“相伴方程”.
(1)判断方程6﹣4(1﹣x)=2x与是否为“相似方程”,并说明理由;
(2)已知关于x,y的二元一次方程y=mx+6和y=x+4m是“相伴方程”,求正整数m的值.
13.(2022秋 海安市期末)阅读材料:对于非零实数a,b,若关于x的分式的值为零,则解得x1=a,x2=b.又因为x(a+b),所以关于x的方程x(a+b),的解为x1=a,x2=b.
(1)理解应用:方程3的解为:x1= ,x2= ;
(2)知识迁移:若关于x的方程x5的解为x1=a,x2=b,求a2+b2的值;
(3)拓展提升:若关于x的方程k﹣x的解为x1,x2,且x1x2=1,求k的值.
14.(2024春 姑苏区期末)如图,一次函数y=kx+b的图象与反比例函数的图象交于A(1,6),B(3,n)两点,与x轴交于点C.
(1)求一次函数与反比例函数的表达式;
(2)连接OA,OB,求△AOB的面积.
15.(2022春 宿迁期末)如图,一次函数y1=ax+b与反比例函数y2的图象相交于A(2,8),B(8,2)两点,连接AO,BO,延长AO交反比例函数图象于点C.
(1)求一次函数y1的表达式与反比例函数y2的表达式;
(2)当y1<y2,时,直接写出自变量x的取值范围为 ;
(3)点P是x轴上一点,当S△PACS△AOB时,请直接写出点P的坐标为 .
16.(2024春 连云港期末)心理学研究发现,一般情况下,在一节45分钟的课中,学生的注意力随学习时间的变化而变化.开始学习时,学生的注意力逐步增强,中间有一段时间学生的注意力保持较为理想的稳定状态,随后学生的注意力开始分散.经过实验分析可知,学生的注意力指标数y随时间x(分钟)的变化规律如图所示(其中AB、BC分别为线段,CD为双曲线的一部分).
(1)开始学习后第5分钟时与第35分钟时相比较,何时学生的注意力更集中?为什么?
(2)某些数学内容的课堂学习大致可分为三个环节:即“教师引导,回顾旧知﹣﹣自主探索,合作交流﹣﹣总结归纳,巩固提高”.其中重点环节“自主探索,合作交流”这一过程一般需要30分钟才能完成,为了确保效果,要求学习时的注意力指标数不低于40.请问这样的课堂学习安排是否合理?并说明理由.
17.(2024春 泗阳县期末)已知反比例函数y(k常数,k≠2).
(1)若点A(1,2)在这个函数的图象上,求k的值;
(2)若这个函数图象的每一支上,y都随x的增大而增大,求k的取值范围;
(3)若k=8,试写出当﹣3≤y≤﹣2时x的取值范围.
18.(2022春 淮阴区期末)如图,在平面直角坐标系中,直线y1=k1x+b与双曲线y2相交于A(﹣2,3),B(m,﹣2)两点.
(1)求y1、y2对应的函数表达式;
(2)过点B作BP∥x轴交y轴于点P,求△ABP的面积.
19.(2024秋 邗江区校级期末)我们在学习二次根式的时候会发现:有时候两个含有二次根式的代数式相乘,积不含有二次根式,如,.课本中阅读材料告诉我们,两个含有二次根式的非零代数式相乘,如果它们的积不是二次根式,那么这两个代数式互为有理化因式.
请运用有理化因式的知识,解决下列问题:
(1)化简: ;
(2)比较大小: ;(用“>”、“=”或“<”填空)
(3)设有理数a、b满足:,则a+b= ;
(4)已知,求的值.
20.(2023秋 沭阳县校级期末)定义:若一个三角形存在两边平方和等于第三边平方的3倍,则称此三角形为“平方倍三角形”.
(1)若一个三角形的三边长分别是,和2,这个三角形是否为平方倍三角形?请你作出判断并说明理由.
(2)若一个直角三角形是平方倍三角形,求该直角三角形的三边之比(结果按从小到大的顺序排列).
【江苏省各地区期末真题汇编】热点题型分类突破:解答题-2024-2025学年数学八年级下册苏科版
参考答案与试题解析
一.解答题(共20小题)
1.(2024秋 惠山区期末)为了解八年级学生每天完成课外作业时间的情况、从全区八年级学生中随机抽取了部分学生每天完成课外作业的时间进行调查,并将调查结果绘制成如下图表:
时间x(小时) 频数y(人数) 频率
0≤x≤0.5 8 0.2
0.5<x≤1 c 0.3
1<x≤1.5 12 0.3
1.5<x≤2 6 b
2<x≤2.5 2 0.05
合计 a 1
(1)表中a,b所表示的数分别为a= 40 ,b= 0.15 ;
(2)请在图中补全频数分布直方图;
(3)根据规定,学生每天完成课外作业的时间不超过1.5小时,那么全区4800名八年级学生中每天完成课外作业时间超过规定的学生约有多少人?
【解答】解:(1)a=8÷0.2=40,b=6÷40=0.15,
故答案为:40、0.15;
(2)c=0.3×40=12,补全图形如下:
(3)4800×(0.15+0.05)=960(人),
答:全区4800名八年级学生中每天完成课外作业时间超过规定的学生约有960人.
2.(2024秋 兴化市期末)有甲、乙两只不透明的袋子,每只袋子中装有红球和黄球若干,各袋中所装球的总个数相同,这些球除颜色外都相同.实践组用甲袋、创新组用乙袋各自做摸球试验:两人一组,一人从袋中任意摸出1个球,另一人记下颜色后将球放回并搅匀,各组连续做这样的试验,将记录的数据绘制成如下两种条形统计图:
(1) B 图能更好地反各组试验的总次数, A 图能更好地反映各组试验摸到红球的频数(填“A”或“B”);
(2)求实践组摸到黄球的频率;
(3)实践组摸到黄球的频率 小于 创新组摸到黄球的频率(填“大于”、“小于”或“等于”).
【解答】解:(1)B图能更好地反映各组试验的总次数,A图能更好地反映各组试验摸到红球的频数;
故答案为:B,A.
(2)实践组摸到黄球的频率=(500﹣372)÷500=0.256;
(3)实践组摸到黄球的频率小于创新组摸到黄球的频率(答案不唯一).
3.(2024春 响水县期末)每年的6月5日是“世界环境日”.某中学“环保小卫士”研学小组对周边小区部分居民开展了以“爱护环境,从我做起”为主题的问卷调查,调查内容如下:
A:能将垃圾放到规定地点,并会考虑垃圾分类;
B:能将垃圾放到规定地点,但不会考虑垃圾分类;
C:基本能将垃圾放到规定地点,偶尔会乱扔垃圾;
每人都选且只选一项,研学小组将调查结果制成两幅不完整的统计图:
(1)研学小组一共调查了 1000 人;请将条形统计图补充完整;
(2)求扇形统计图中C对应的扇形圆心角的度数;
(3)如果你是“环保小卫士”,请根据以上调查结果,谈谈你的想法.
【解答】解:(1)500÷50%=1000(人),
所以研学小组一共调查了1000人;
B处理方式的人数为:1000﹣500﹣100=400(人),
补全条形统计图,如图所示:
(2)C处理方式的百分比为:100%﹣50%﹣40%=10%,
扇形统计图中C对应的扇形圆心角的度数为:360°×10%=36°.
(3)将垃圾放到规定地点,并分类放置,保护环境,从自身做起.(答案不唯一)
4.(2024秋 宝应县期末)在一只不透明的口袋里,装有若干个除了颜色外均相同的小球,某数学学习小组做摸球试验,将球搅匀后从中随机摸出一个球记下颜色,再把它放回袋中,不断重复.如表是活动进行中的一组统计数据:
摸球的次数n 100 150 200 500 800 1000
摸到白球的次数m 59 96 b 295 480 601
摸到白球的频率 a 0.64 0.58 0.59 0.60 0.601
(1)上表中的a= 0.59 ,b= 116 ;
(2)“摸到白球的”的概率的估计值是 0.6 (精确到0.1);
(3)如果袋中有12个白球,那么袋中除了白球外,还有多少个其它颜色的球?
【解答】解:(1)a=59÷100=0.59,b=200×0.58=116.
故答案为:0.59,116
(2)“摸到白球的”的概率的估计值是0.6;
故答案为:0.6
(3)12÷0.6﹣12=8(个).
答:除白球外,还有大约8个其它颜色的小球;
5.(2024春 广陵区期末)在一个不透明的袋子里装有只有颜色不同的黑、白两种颜色的球共50个,某学习小组做摸球试验,将球搅匀后从中随机摸出一个球记下颜色,再把它放回袋中,不断重复,下表是活动进行中的一组统计数据:
摸球的次数n 1000 2000 3000 5000 8000 10000
摸到黑球的次数m 650 1180 1890 3100 4820 6013
摸到黑球的频率 0.65 0.59 0.63 0.62 0.6025 0.6013
(1)请估计:当n很大时,摸到黑球的频率将会接近 0.6 (精确到0.1);
(2)试估计袋子中有黑球 30 个;
(3)若学习小组通过试验结果,想使得在这个不透明袋子中每次摸到黑球的可能性大小为50%,则可以在袋子中增加相同的白球 10 个或减少黑球 10 个.
【解答】解:(1)观察表格得:当n很大时,摸到黑球的频率将会接近0.6,
故答案为:0.6;
(2)黑球的个数为50×0.6=30个,
故答案为:30;
(3)想使得在这个不透明袋子中每次摸到黑球的可能性大小为50%,则可以使得黑球和白球的个数相同,
即:在袋子中增加相同的白球10个或减少黑球10个,
故答案为:10,10.
6.(2024春 姑苏区期末)如图,在△ABC中,∠BAC=90°,AD是斜边上的中线,E是AD的中点,过点A作AF∥BC交BE的延长线于F,连接CF.
(1)求证:BD=AF;
(2)判断四边形ADCF的形状,并证明你的结论.
【解答】(1)证明:∵AF∥BC,
∴∠AFE=∠DBE,
∵E是AD的中点,AD是BC边上的中线,
∴AE=DE,BD=CD,
在△AFE和△DBE中,,
∴△AFE≌△DBE(AAS),
∴BD=AF;
(2)解:四边形ADCF是菱形;理由如下:
由(1)知,AF=DB.
∵DB=DC,
∴AF=CD.
∵AF∥BC,
∴四边形ADCF是平行四边形,
∵∠BAC=90°,D是BC的中点,
∴AD=DCBC,
∴四边形ADCF是菱形.
7.(2023春 玄武区期末)如图,在△ABC中,∠ACB=90°,D、E分别是AB、AC的中点,过点C作CF∥AB,交DE延长线于点F,连接AF、CD.
(1)求证:四边形ADCF是菱形;
(2)当 时,四边形ADCF是正方形.
【解答】(1)证明:∵D、E分别是AB、AC中点,
∴DE是△ABC的中位线,
∴DE∥BC,
又∵CF∥AB,
∴四边形DBCF是平行四边形,
∴CF=BD,
∵D是AB的中点,
∴AD=BD,
∴CF=AD,
又∵CF∥AB,
∴四边形ADCF是平行四边形,
∵∠ACB=90°,D是AB中点,
∴.
∴CD=AD.
又∵四边形ADCF是平行四边形,
∴四边形ADCF是菱形;
(2)解:当时,四边形ADCF是正方形.
∵∠ACB=90°,
∴设ABk,AC=k,
∴BCk,
∴AC=BC,
∴△ABC是等腰直角三角形,
∵D是AB的中点,
∴CD⊥AB,
∴∠ADC=90°,
由(1)知,四边形ADCF是菱形,
∴四边形ADCF是正方形.
故答案为:.
8.(2024春 邗江区期末)如图,在 ABCD中,∠ABD的平分线BE交AD于点E,∠CDB的平分线DF交BC于点F.
(1)求证:△ABE≌△CDF;
(2)若AB=DB,求证:四边形DFBE是矩形.
【解答】证明:(1)∵∠ABD的平分线BE交AD于点E,
∴∠ABE∠ABD,
∵∠CDB的平分线DF交BC于点F,
∴∠CDF∠CDB,
∵在平行四边形ABCD中,
∴AB∥CD,
∴∠ABD=∠CDB,
∴∠CDF=∠ABE,
∵四边形ABCD是平行四边形,
∴CD=AB,∠A=∠C,
即,
∴△ABE≌△CDF(ASA);
(2)∵△ABE≌△CDF,
∴AE=CF,
∵四边形ABCD是平行四边形,
∴AD∥BC,AD=BC,
∴DE∥BF,DE=BF,
∴四边形DFBE是平行四边形,
∵AB=DB,BE平分∠ABD,
∴BE⊥AD,即∠DEB=90°.
∴平行四边形DFBE是矩形.
9.(2023春 亭湖区校级期末)如图, ABCD对角线AC,BD相交于点O,过点D作DE∥AC且DE=OC,连接CE,OE,OE=CD.
(1)求证: ABCD是菱形;
(2)若AB=4,∠ABC=60°,求AE的长.
【解答】(1)证明:∵DE∥AC,DE=OC,
∴四边形OCED是平行四边形.
∵OE=CD,
∴平行四边形OCED是矩形,
∴∠COD=90°,
∴AC⊥BD,
∴ ABCD是菱形;
(2)解:∵四边形ABCD是菱形,
∴OA=OC,CD=AB=BC=4,AC⊥BD,
∵∠ABC=60°,
∴△ABC是等边三角形,
∴AC=AB=4,
∴OA=OC=2,
在Rt△OCD中,由勾股定理得:OD2,
由(1)可知,四边形OCED是矩形,
∴CE=OD=2,∠OCE=90°,
∴AE2,
即AE的长为2.
10.(2024秋 如东县期末)【追本溯源】题(1)来自于课本中的习题,请你完成解答,提炼方法并完成题(2).
(1)如图1,AD∥BC,BD平分∠ABC.求证:AB=AD.
【方法应用】
(2)如图2,AD∥BC,AB∥DC,BE平分∠ABC,交边AD于点E,过点A作AF⊥BE交DC的延长线于点F.若AD=6,CD=3.5,求CF的长.
【解答】(1)证明:∵BD平分∠ABC,
∴∠ABD=∠CBD.
∵AD∥BC,
∴∠ADB=∠CBD,
∴∠ADB=∠ABD,
∴AB=AD;
(2)解:∵AD∥BC,AB∥CD,
∴四边形ABCD是平行四边形,∠BAF=∠F,
∴BC=AD=6,AB=CD=3.5,
由(1)可知,∠ABE=∠EBG=∠AEB,AB=AE,
∵AF⊥BE,
∴∠BAF=∠EAF,
∴∠EAF=∠F,
∴DF=AD=6,
∴CF=DF﹣CD=6﹣3.5=2.5.
11.(2021春 广陵区校级期末)随着人们“节能环保,绿色出行”意识的增强,越来越多的人喜欢骑自行车出行,也给自行车商家带来商机.某自行车行经营的A型自行车去年销售总额为8万元.今年该型自行车每辆售价预计比去年降低200元.若该型车的销售数量与去年相同,那么今年的销售总额将比去年减少10%,求:A型自行车去年每辆售价多少元?
【解答】解:设去年A型车每辆售价x元,则今年售价每辆为(x﹣200)元,
由题意,得,
解得:x=2000.
经检验,x=2000是原方程的根.
答:去年A型车每辆售价为2000元.
12.(2024秋 宿城区校级期末)对于一些特殊的方程,我们给出两个定义:①若两个方程有相同的解,则称这两个方程为“相似方程”;②若两个方程有相同的整数解,则称这两个方程为“相伴方程”.
(1)判断方程6﹣4(1﹣x)=2x与是否为“相似方程”,并说明理由;
(2)已知关于x,y的二元一次方程y=mx+6和y=x+4m是“相伴方程”,求正整数m的值.
【解答】解:(1)方程6﹣4(1﹣x)=2x与方程是“相似方程”,理由如下:
解方程6﹣4(1﹣x)=2x得:x=﹣1,
解方程得:x=﹣1,
检验:x=﹣1是该分式方程得解.
∴两个方程是“相似方程”;
(2)由条件可知mx+6=x+4m,
,
∵x,y,m均为整数,
∴m﹣1=±1,m﹣1=±2,
∴m1=0,m2=2,m3=﹣1,m4=3,
又∵m为正整数,
∴m=2或m=3.
13.(2022秋 海安市期末)阅读材料:对于非零实数a,b,若关于x的分式的值为零,则解得x1=a,x2=b.又因为x(a+b),所以关于x的方程x(a+b),的解为x1=a,x2=b.
(1)理解应用:方程3的解为:x1= 3 ,x2= ;
(2)知识迁移:若关于x的方程x5的解为x1=a,x2=b,求a2+b2的值;
(3)拓展提升:若关于x的方程k﹣x的解为x1,x2,且x1x2=1,求k的值.
【解答】解:(1)∵xa+b的解为x1=a,x2=b,
∴的解为x=3或x,
故答案为:3,;
(2)∵x5,
∴a+b=5,ab=3,
∴a2+b2=(a+b)2﹣2ab=25﹣6=19;
(3)k﹣x可化为x2﹣(k+1)x+4+k=0,
∵x1x2=1,
∴4+k=1,
∴k=﹣3.
14.(2024春 姑苏区期末)如图,一次函数y=kx+b的图象与反比例函数的图象交于A(1,6),B(3,n)两点,与x轴交于点C.
(1)求一次函数与反比例函数的表达式;
(2)连接OA,OB,求△AOB的面积.
【解答】解:(1)∵一次函数y=kx+b的图象与反比例函数y(x>0)的图象交于A(1,6),B(3,n)两点,
∴m=6×1=3×n,
∴m=6,n=2,
∵,
解得:,
∴一次函数解析式y=﹣2x+8,
反比例函数的解析式y.
(2)∵一次函数解析式y=﹣2x+8图象交x轴为点C,
∴C(4,0),
∵△AOB面积=△AOC面积﹣△COB面积4×64×2=12﹣4=8.
15.(2022春 宿迁期末)如图,一次函数y1=ax+b与反比例函数y2的图象相交于A(2,8),B(8,2)两点,连接AO,BO,延长AO交反比例函数图象于点C.
(1)求一次函数y1的表达式与反比例函数y2的表达式;
(2)当y1<y2,时,直接写出自变量x的取值范围为 x>8或0<x<2 ;
(3)点P是x轴上一点,当S△PACS△AOB时,请直接写出点P的坐标为 P(3,0)或P(﹣3,0) .
【解答】解:(1)将A(2,8),B(8,2)代入y1=ax+b得,
解得,
∴一次函数为y1=﹣x+10,
将A(2,8)代入y2得8,解得k=16,
∴反比例函数的解析式为y2;
(2)由图象可知,当y1<y2时,自变量x的取值范围为:x>8或0<x<2,
故答案为x>8或0<x<2;
(3)由题意可知OA=OC,
∴S△APC=2S△AOP,
把y=0代入y1=﹣x+10得,0=﹣x+10,解得x=10,
∴D(10,0),
∴S△AOB=S△AOD﹣S△BOD30,
∵S△PACS△AOB30=24,
∴2S△AOP=24,
∴2yA=24,即2OP×8=24,
∴OP=3,
∴P(3,0)或P(﹣3,0),
故答案为P(3,0)或P(﹣3,0).
16.(2024春 连云港期末)心理学研究发现,一般情况下,在一节45分钟的课中,学生的注意力随学习时间的变化而变化.开始学习时,学生的注意力逐步增强,中间有一段时间学生的注意力保持较为理想的稳定状态,随后学生的注意力开始分散.经过实验分析可知,学生的注意力指标数y随时间x(分钟)的变化规律如图所示(其中AB、BC分别为线段,CD为双曲线的一部分).
(1)开始学习后第5分钟时与第35分钟时相比较,何时学生的注意力更集中?为什么?
(2)某些数学内容的课堂学习大致可分为三个环节:即“教师引导,回顾旧知﹣﹣自主探索,合作交流﹣﹣总结归纳,巩固提高”.其中重点环节“自主探索,合作交流”这一过程一般需要30分钟才能完成,为了确保效果,要求学习时的注意力指标数不低于40.请问这样的课堂学习安排是否合理?并说明理由.
【解答】解:(1)设yAB=k1x+b,把(0,20),(10,50)代入函数解析式解得yAB=3x+20(0≤x≤10),
由图象直接得到yBC=50(10≤x≤30),
设yCD,把(30,50)代入函数解析式解得yCD(30≤x≤45);
把x=5代入yAB=3x+20,得yAB=35,
把x=35代入yCD,得yCD,
因为yAB≤yCD,
所以第35分钟时学生的注意力更集中;
(2)由题意知,注意力指数不低于40
即当在3x+20≥40,x
同时40
即x37.5
即当开始上课分钟直至上课37.5分钟时学生的注意力指数均不小于40.
而37.530,
∴该学习设计合理.
17.(2024春 泗阳县期末)已知反比例函数y(k常数,k≠2).
(1)若点A(1,2)在这个函数的图象上,求k的值;
(2)若这个函数图象的每一支上,y都随x的增大而增大,求k的取值范围;
(3)若k=8,试写出当﹣3≤y≤﹣2时x的取值范围.
【解答】解:(1)把点A(1,2)代入反比例函数y得:k﹣2=1×2,
∴k=4
因此k的值为:4;
(2)反比例函数y每一支上,y都随x的增大而增大,
∴k﹣2<0,
∴k<2;
(3)当k=8时,反比例函数的关系式为y,此时在每个象限内,y随x的增大而减小,
当y=﹣3时,x=﹣2,
当y=﹣2时,x=﹣3,
∴x的取值范围为:﹣3≤x≤﹣2.
18.(2022春 淮阴区期末)如图,在平面直角坐标系中,直线y1=k1x+b与双曲线y2相交于A(﹣2,3),B(m,﹣2)两点.
(1)求y1、y2对应的函数表达式;
(2)过点B作BP∥x轴交y轴于点P,求△ABP的面积.
【解答】解:(1)∵直线y1=k1x+b与双曲线y2相交于A(﹣2,3),B(m,﹣2)两点,
∴k2=﹣2×3=﹣2m
∴k2=﹣6,m=3,
∴双曲线的表达式为:y2,B(3,﹣2),
把A(﹣2,3)和B(3,﹣2)代入y1=k1x+b得:,
解得:,
∴直线的表达式为:y1=﹣x+1;
(2)∵BP∥x轴,B(3,﹣2),
∴BP=3,
∴S△ABP.
19.(2024秋 邗江区校级期末)我们在学习二次根式的时候会发现:有时候两个含有二次根式的代数式相乘,积不含有二次根式,如,.课本中阅读材料告诉我们,两个含有二次根式的非零代数式相乘,如果它们的积不是二次根式,那么这两个代数式互为有理化因式.
请运用有理化因式的知识,解决下列问题:
(1)化简: ;
(2)比较大小: < ;(用“>”、“=”或“<”填空)
(3)设有理数a、b满足:,则a+b= ﹣6 ;
(4)已知,求的值.
【解答】解:(1)原式.
故答案为:;
(2)∵,,
∵,
∴;
故答案为:<;
(3)∵,
∴(1)a+(1)b=﹣64,
∴(a+b)a+b=﹣64,
∵a,b是有理数,
∴a+b=﹣6,﹣a+b=4.
故答案为:﹣6;
(4)∵,
∴,
∴,
∴3.
20.(2023秋 沭阳县校级期末)定义:若一个三角形存在两边平方和等于第三边平方的3倍,则称此三角形为“平方倍三角形”.
(1)若一个三角形的三边长分别是,和2,这个三角形是否为平方倍三角形?请你作出判断并说明理由.
(2)若一个直角三角形是平方倍三角形,求该直角三角形的三边之比(结果按从小到大的顺序排列).
【解答】解:(1)结论:这个三角形是“平方倍三角形”.理由如下:
∵()2+22=15,3×()2=15,
∴()2+22=3×()2,
∴这个三角形是“平方倍三角形”.
(2)设两直角边长为:a,b,斜边长为:c,
∵△ABC为“平方倍三角形”.
∴a2+b2=c2,且c2+a2=3b2,
∴2a2+b2=3b2,
∴b=a,
∴ca,
∴a:b:c=1:1:.
21世纪教育网 www.21cnjy.com 精品试卷·第 2 页 (共 2 页)
21世纪教育网(www.21cnjy.com)
同课章节目录
