【江苏省各地区期末真题汇编】热点题型分类突破:解答题(含解析)-2024-2025学年数学七年级下册苏科版(2024)
文档属性
| 名称 | 【江苏省各地区期末真题汇编】热点题型分类突破:解答题(含解析)-2024-2025学年数学七年级下册苏科版(2024) |  | |
| 格式 | docx | ||
| 文件大小 | 974.5KB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 苏科版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2025-05-30 15:25:00 | ||
图片预览



文档简介
中小学教育资源及组卷应用平台
【江苏省各地区期末真题汇编】热点题型分类突破:解答题-2024-2024学年数学七年级下册苏科版(2024)
1.(2024春 赣榆区期末)若am=an(a>0且a≠1,m,n是正整数),则m=n.试利用该结论求x的值:3×9x×81=321.
2.(2024春 徐州期末)在幂的运算中规定:若ax=ay(a>0且a≠1,x,y是正整数),则x=y.
(1)如果2×4x=219,求x的值;
(2)如果5x+2﹣5x+1=500,求x的值.
3.(2024春 海陵区期末)比较两个底数大于1的正数幂的大小,可以在底数(或指数)相同的情况下,比较指数(或底数)的大小,如:25>23,55>45.
(1)比较254,1253的大小.
(2)比较3555,4444,5333的大小.
4.(2024春 宜兴市期末)如果ac=b,那么我们规定(a,b)=c,例如:因为23=8,所以(2,8)=3
(1)根据上述规定,填空:
(3,27)= ,(4,1)= (2,0.25)= ;
(2)记(3,5)=a,(3,6)=b,(3,30)=c.求证:a+b=c.
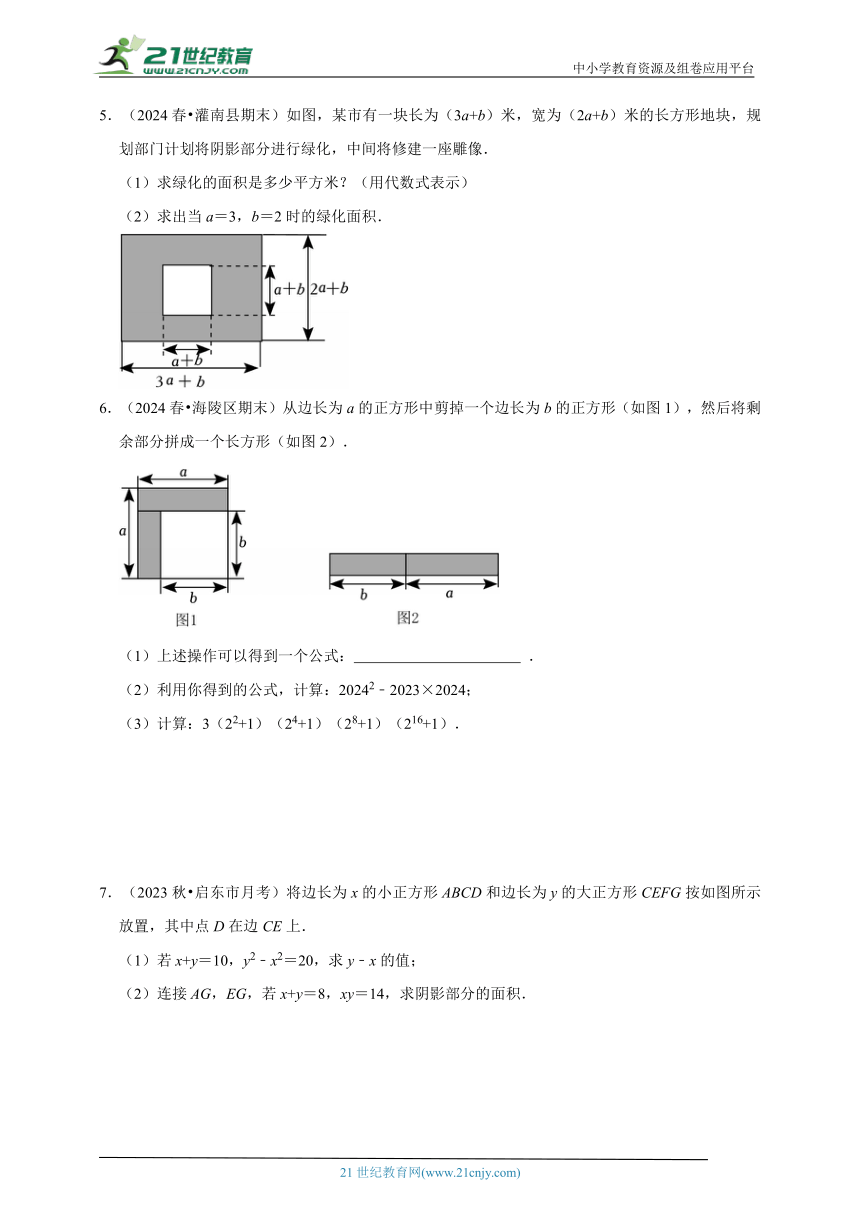
5.(2024春 灌南县期末)如图,某市有一块长为(3a+b)米,宽为(2a+b)米的长方形地块,规划部门计划将阴影部分进行绿化,中间将修建一座雕像.
(1)求绿化的面积是多少平方米?(用代数式表示)
(2)求出当a=3,b=2时的绿化面积.
6.(2024春 海陵区期末)从边长为a的正方形中剪掉一个边长为b的正方形(如图1),然后将剩余部分拼成一个长方形(如图2).
(1)上述操作可以得到一个公式: .
(2)利用你得到的公式,计算:20242﹣2023×2024;
(3)计算:3(22+1)(24+1)(28+1)(216+1).
7.(2023秋 启东市月考)将边长为x的小正方形ABCD和边长为y的大正方形CEFG按如图所示放置,其中点D在边CE上.
(1)若x+y=10,y2﹣x2=20,求y﹣x的值;
(2)连接AG,EG,若x+y=8,xy=14,求阴影部分的面积.
8.(2024春 高新区月考)【知识回顾】
我们在学习代数式求值时,遇到这样一类题:代数式ax﹣y+6+3x一5y﹣1的值与x的取值无关,求a的值.
通常的解题思路是:把x、y看作字母,a看作系数,合并同类项.因为代数式的值与x的取值无关,所以含x项的系数为0.
具体解题过程是:原式(a+3)x﹣6y+5,
∵代数式的值与x的取值无关,
∴a+3=0,解a=﹣3.
【理解应用】
(1)若关于x的代数式mx﹣4x+3的值与x的取值无关,则m值为 .
(2)已知A=(2x+1)(x﹣2),B=x(m﹣x),且A+2B的值与x的取值无关,求m的值.
【能力提升】
(3)7张如图1的小长方形,长为a,宽为b,按照图2方式不重叠地放在大长方形ABCD内,大长方形中未被覆盖的两个部分都是长方形.设右上角的面积为S1,左下角的面积为S2,当AB的长变化时,S1﹣S2的值始终保持不变,求a与b的等量关系.
9.(2024春 苏州校级期末)如图,将△ABC沿BC方向平移,得到△DEF.
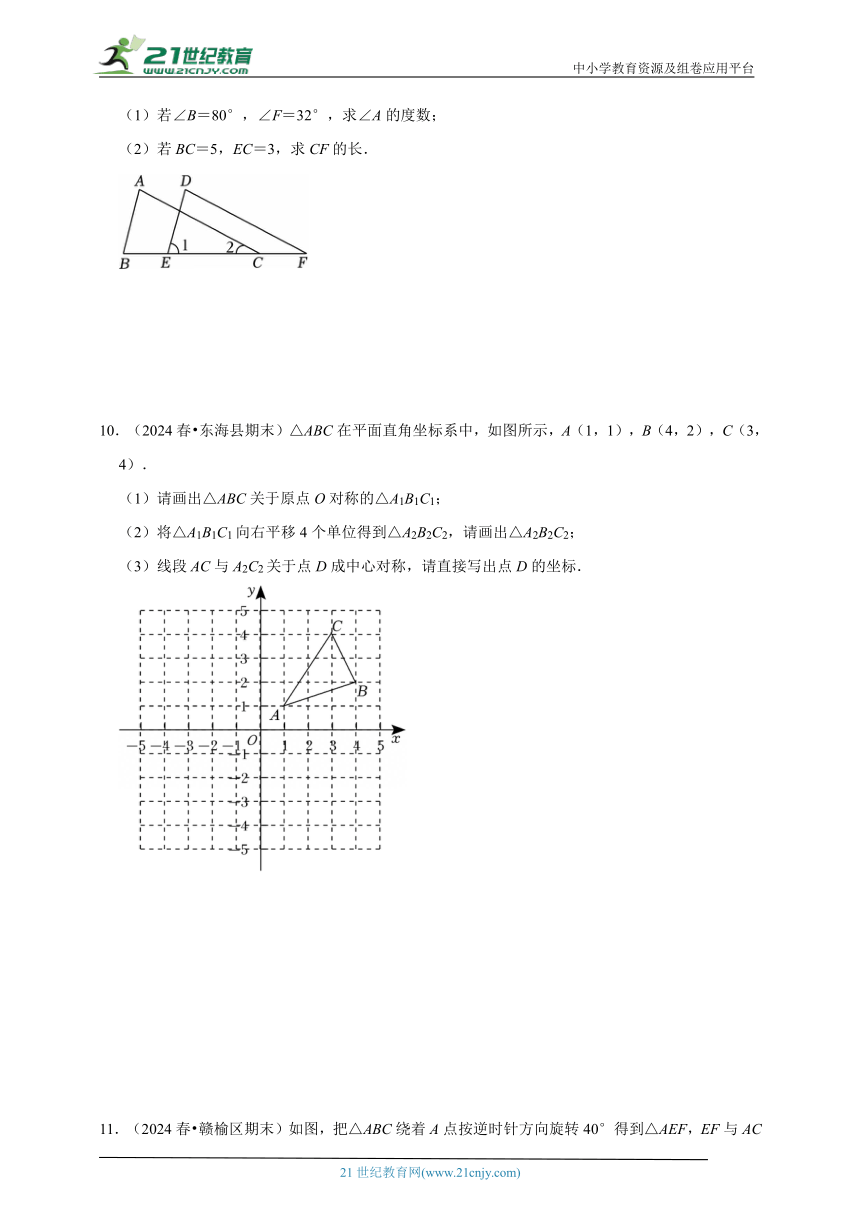
(1)若∠B=80°,∠F=32°,求∠A的度数;
(2)若BC=5,EC=3,求CF的长.
10.(2024春 东海县期末)△ABC在平面直角坐标系中,如图所示,A(1,1),B(4,2),C(3,4).
(1)请画出△ABC关于原点O对称的△A1B1C1;
(2)将△A1B1C1向右平移4个单位得到△A2B2C2,请画出△A2B2C2;
(3)线段AC与A2C2关于点D成中心对称,请直接写出点D的坐标.
11.(2024春 赣榆区期末)如图,把△ABC绕着A点按逆时针方向旋转40°得到△AEF,EF与AC交于点D点,若∠ADF=90°,求∠C的度数.
12.(2024春 锡山区期末)如图,将三角形ABC沿射线BC方向平移得到三角形DEF,点A,B,C的对应点分别是点D,E,F.
(1)若∠DAC=60°,求∠DFE的度数;
(2)若BF=15,BE=CE,求平移的距离;
(3)在(2)的条件下,若三角形ABC的周长为25,求四边形ABFD的周长.
13.(2024 铜山区二模)算盘是我国优秀文化遗产.它以排列成串的算珠作为计算工具,中间横梁把算珠分为上、下两部分,每个上珠代表5,每个下珠代表1.如图,小华在百位拨了一颗上珠和一颗下珠,然后对小明说:我将要拨的三位数,个位数字与十位数字之和是百位数字的2倍;个位数字减2等于十位数字加2,请求出这个三位数.
14.(2024春 沛县月考)某体育用品商场销售A,B两款足球,售价和进价如表所示:
类型 进价/(元/个) 售价/(元/个)
A款 m 120
B款 n 90
若该商场购进4个A款足球和11个B款足球需980元;购进2个A款足球和3个B款足球需340元.
(1)求m和n的值.
(2)某校在该商场一次性购买A款足球x个和B款足球y个,共消费3000元,那么该商场可获利多少元?
(3)为了提高销量,商场实施:“买足球送跳绳”的促销活动:“买1个A款足球送1根跳绳,买3个B款足球送2根跳绳”,每根跳绳的成本为10元,某日售卖出两款足球总计盈利600元,那么该日商场销售A,B两款足球各多少个(每款都有销售)?
15.(2024 泰兴市二模)某公司组织50名员工外出团建,有两种出行方案及对应费用如表:
方案类型 坐动车人数 坐飞机人数 总费用
方案一 10人 40人 24000元
方案二 15人 35人 23750元
根据表中信息,求动车和飞机票价分别是多少元?
16.(2024春 海门区期末)为了解决民工子女入学难的问题,我市建立了一套进城民工子女就学的保障机制,其中一项就是免交“借读费”.据统计,去年秋季有5000名民工子女进入主城区中小学学习,预测今年秋季进入主城区中小学学习的民工子女将比去年有所增加,其中小学增加20%,中学增加30%,这样今年秋季将新增1160名民工子女在主城区中小学学习.
(1)如果按小学每年收“借读费”500元、中学每年收“借读费”1000元计算,求今年秋季新增的1160名中小学生共免收多少“借读费”;
(2)如果小学每40名学生配备2名教师,中学每40名学生配备3名教师,按今年秋季入学后,民工子女在主城区中小学就读的学生人数计算,一共需配备多少名中小学教师?
17.(2024春 南京期末)某校计划创建大小图书角共20个,现有图书3200册,其中每个小图书角需图书100册,每个大图书角需图书250册,问该校创建的大小图书角分别有多少个?
(1)小亮根据题意,列出方程组,请分别指出未知数x,y表示的意义:x表示 ,y表示 .
(2)小丽“设该校创建的大图书角m个,小图书角n个”,请按照小丽的思路列出方程组,并求m,n的值.
18.(2024春 丹阳市期末)【定义】我们把关于x、y的两个二元一次方程ax+by=c与bx+ay=c(a≠b)叫作“对称二元一次方程”,二元一次方程组叫做关于x、y的“对称二元一次方程组”.例如:2x+y=3与x+2y=3是“对称二元一次方程”,二元一次方程组叫做关于x、y的“对称二元一次方程组”.
【理解】
(1)方程2x﹣3y=5的“对称二元一次方程”是 ;
(2)若关于x、y的方程组为“对称二元一次方程组”,则a= ,b= ;
【探究】
(3)解下列方程组(直接写出方程组的解):
①的解为 ;
②的解为 ;
③的解为 ;
(4)根据你的发现,直接写出方程组的解为 ;
【拓展】
(5)若关于x、y的方程组的解是,那么关于x、y的方程组的解为 .
19.(2024春 高新区校级月考)某工厂计划生产A、B两种产品共10件,其生产成本和利润如表:
A种产品 B种产品
成本(万元/件) 2 5
利润(万元/件) 1 3
(1)若工厂计划获利14万元,问A、B两种产品应分别生产多少件?
(2)若工厂计划投入资金不多于44万元,且获利多于20万元,问工厂有哪几种生产方案?
(3)在(2)的条件下,哪种生产方案获利最大?并求出最大利润.
20.(2024春 沛县月考)阅读下列材料:
[数学问题]已知x﹣y=2,且x>1,y<0,试确定x+y的取值范围.
[问题解决]∵x﹣y=2,∴x=y+2.
又∵x>1,
∴y+2>1,∴y>﹣1.
又∵y<0,
∴﹣1<y<0.①
同理得:1<x<2.②
由①+②得:﹣1+1<x+y<0+2.
即:0<x+y<2.
[类比探究]
(1)在数学问题中的条件下,x+2y的取值范围是 .
(2)已知x﹣y=5,且x>2,y<0,
①求y的取值范围.
②求x+2y的取值范围.
(3)已知y≥1,x<﹣1,若x+y=a(a>0),直接写出x﹣2y的取值范围(用含a的代数式表示).
21.(2024春 亭湖区校级期末)如图,①AB∥CD,②BE平分∠ABD,③DE平分∠BDC,④∠1+∠2=90°.(1)若以①②③为条件,④为结论组成一个命题,则这个命题是 (“真”或“假”)命题;
(2)若(1)为真命题,证明(1)中的结论:若(1)为假命题,请举出反例.
22.(2024春 睢宁县期末)如图,从①∠1=∠2②∠C=∠D③∠A=∠F三个条件中选出两个作为已知条件,另一个作为结论可以组成3个命题.
(1)这三个命题中,真命题的个数为 ;
(2)选择一个真命题,并且证明,(要求写出每一步的依据)
如图,已知 ,
求证:
证明:
【江苏省各地区期末真题汇编】热点题型分类突破:解答题-2024-2024学年数学七年级下册苏科版(2024)
参考答案与试题解析
一.解答题(共22小题)
1.(2024春 赣榆区期末)若am=an(a>0且a≠1,m,n是正整数),则m=n.试利用该结论求x的值:3×9x×81=321.
【解答】解:∵3×9x×81=3×32x×34=31+2x+4=32x+5,
∴2x+5=21,
∴x=8.
2.(2024春 徐州期末)在幂的运算中规定:若ax=ay(a>0且a≠1,x,y是正整数),则x=y.
(1)如果2×4x=219,求x的值;
(2)如果5x+2﹣5x+1=500,求x的值.
【解答】解:(1)由条件可得2×(22)x=219,
∴2×22x=219,22x+1=219,
∴2x+1=19,
解得:x=9;
(2)由条件可知5x+1(5﹣1)=53×4,
∴5x+1=53,
∴x+1=3,
解得:x=2.
3.(2024春 海陵区期末)比较两个底数大于1的正数幂的大小,可以在底数(或指数)相同的情况下,比较指数(或底数)的大小,如:25>23,55>45.
(1)比较254,1253的大小.
(2)比较3555,4444,5333的大小.
【解答】解:(1)254=(52)4=58,
1253=(53)3=59,
∵58<59,
∴254<1253.
(2)3555=(35)111=243111,
4444=(44)111=256111,
5333=(53)111=125111.
∵256111>243111>125111,
∴4444>3555>5333.
4.(2024春 宜兴市期末)如果ac=b,那么我们规定(a,b)=c,例如:因为23=8,所以(2,8)=3
(1)根据上述规定,填空:
(3,27)= 3 ,(4,1)= 0 (2,0.25)= ﹣2 ;
(2)记(3,5)=a,(3,6)=b,(3,30)=c.求证:a+b=c.
【解答】解:(1)(3,27)=3,(4,1)=0,(2,0.25)=﹣2,
故答案为:3,0,﹣2;
(2)证明:∵(3,5)=a,(3,6)=b,(3,30)=c,
∴3a=5,3b=6,3c=30,
∴3a×3b=30,
∴3a×3b=3c,
∴a+b=c.
5.(2024春 灌南县期末)如图,某市有一块长为(3a+b)米,宽为(2a+b)米的长方形地块,规划部门计划将阴影部分进行绿化,中间将修建一座雕像.
(1)求绿化的面积是多少平方米?(用代数式表示)
(2)求出当a=3,b=2时的绿化面积.
【解答】解:(1)阴影部分的面积=(3a+b)(2a+b)﹣(a+b)2
=6a2+5ab+b2﹣a2﹣2ab﹣b2
=5a2+3ab;
(2)当a=3,b=2时,原式=5×32+3×3×2=63(平方米).
6.(2024春 海陵区期末)从边长为a的正方形中剪掉一个边长为b的正方形(如图1),然后将剩余部分拼成一个长方形(如图2).
(1)上述操作可以得到一个公式: a2﹣b2=(a+b)(a﹣b) .
(2)利用你得到的公式,计算:20242﹣2023×2024;
(3)计算:3(22+1)(24+1)(28+1)(216+1).
【解答】解:(1)图1中阴影部分可以看作两个正方形的面积差,即a2﹣b2,拼成的图2是长为a+b,宽为a﹣b的长方形,因此面积为(a+b)(a﹣b),
所以有a2﹣b2=(a+b)(a﹣b),
故答案为:a2﹣b2=(a+b)(a﹣b);
(2)原式=20242﹣(2024﹣1)(2024+1)
=20242﹣20242+1
=1;
(3)原式=(22﹣1)(22+1)(24+1)(28+1)(216+1)
=(24﹣1)(24+1)(28+1)(216+1)
=(28﹣1)(28+1)(216+1)
=(216﹣1)(216+1)
=232﹣1.
7.(2023秋 启东市月考)将边长为x的小正方形ABCD和边长为y的大正方形CEFG按如图所示放置,其中点D在边CE上.
(1)若x+y=10,y2﹣x2=20,求y﹣x的值;
(2)连接AG,EG,若x+y=8,xy=14,求阴影部分的面积.
【解答】解:(1)∵y2﹣x2=20,即(y+x)(y﹣x)=20,而x+y=10,
∴y﹣x=2,
答:y﹣x的值为2;
(2)由题意得,
S阴影部分=S正方形ABCD+S正方形CEFG﹣S△ABG﹣S△EFG
=x2+y2x(x+y)y2
x2xyy2
[(x+y)2﹣2xy]xy
当x+y=8,xy=14时,
原式(64﹣28)14
=18﹣7
=11,
答:阴影部分的面积是11.
8.(2024春 高新区月考)【知识回顾】
我们在学习代数式求值时,遇到这样一类题:代数式ax﹣y+6+3x一5y﹣1的值与x的取值无关,求a的值.
通常的解题思路是:把x、y看作字母,a看作系数,合并同类项.因为代数式的值与x的取值无关,所以含x项的系数为0.
具体解题过程是:原式(a+3)x﹣6y+5,
∵代数式的值与x的取值无关,
∴a+3=0,解a=﹣3.
【理解应用】
(1)若关于x的代数式mx﹣4x+3的值与x的取值无关,则m值为 4 .
(2)已知A=(2x+1)(x﹣2),B=x(m﹣x),且A+2B的值与x的取值无关,求m的值.
【能力提升】
(3)7张如图1的小长方形,长为a,宽为b,按照图2方式不重叠地放在大长方形ABCD内,大长方形中未被覆盖的两个部分都是长方形.设右上角的面积为S1,左下角的面积为S2,当AB的长变化时,S1﹣S2的值始终保持不变,求a与b的等量关系.
【解答】解:(1)mx﹣4x+3
=(m﹣4)x+3,
∵关于x的代数式mx﹣4x+3的值与x的取值无关,
∴m﹣4=0,
解得:m=4,
故答案为:4;
(2)∵A=(2x+1)(x﹣2)
=2x2﹣4x+x﹣2
=2x2﹣3x﹣2,
2B=2x(m﹣x)
=2mx﹣2x2,
∴A+2B=2x2﹣3x﹣2+2mx﹣2x2
=2x2﹣2x2+2mx﹣3x﹣2
=2mx﹣3x﹣2
=(2m﹣3)x﹣2,
∵A+2B的值与x无关,
∴2m﹣3=0,
解得:;
(3)设AB=x,由图可知S1=a(x﹣3b),S2=2b(x﹣2a),
∴S1﹣S2
=a(x﹣3b)﹣2b(x﹣2a)
=ax﹣3ab﹣2bx+4ab
=(a﹣2b)x+ab,
∵当AB的长变化时,S1﹣S2的值始终保持不变,
∴S1﹣S2取值与x无关,
∴a﹣2b=0,
∴a=2b.
9.(2024春 苏州校级期末)如图,将△ABC沿BC方向平移,得到△DEF.
(1)若∠B=80°,∠F=32°,求∠A的度数;
(2)若BC=5,EC=3,求CF的长.
【解答】解:(1)因为△DEF由△ABC沿BC方向平移得到,
所以∠2=∠F=32°.
又因为∠B=80°,
所以∠A=180°﹣32°﹣80°=68°.
(2)由平移可知,
EF=BC,
所以EF﹣EC=BC﹣EC,
即CF=BE.
又因为BC=5,EC=3,
所以BE=BC﹣EC=5﹣3=2,
所以CF=BE=2.
10.(2024春 东海县期末)△ABC在平面直角坐标系中,如图所示,A(1,1),B(4,2),C(3,4).
(1)请画出△ABC关于原点O对称的△A1B1C1;
(2)将△A1B1C1向右平移4个单位得到△A2B2C2,请画出△A2B2C2;
(3)线段AC与A2C2关于点D成中心对称,请直接写出点D的坐标.
【解答】解:(1)如图,△A1B1C1即为所求.
(2)如图,△A2B2C2即为所求.
(3)连接AA2,CC2相交于点D,
∴点D的坐标为(2,0).
11.(2024春 赣榆区期末)如图,把△ABC绕着A点按逆时针方向旋转40°得到△AEF,EF与AC交于点D点,若∠ADF=90°,求∠C的度数.
【解答】解:∵把△ABC绕着A点按逆时针方向旋转40°得到△AEF,
∴∠C=∠F,∠DAF=40°,
而∠ADF=90°,
∴∠C=∠F=50°.
12.(2024春 锡山区期末)如图,将三角形ABC沿射线BC方向平移得到三角形DEF,点A,B,C的对应点分别是点D,E,F.
(1)若∠DAC=60°,求∠DFE的度数;
(2)若BF=15,BE=CE,求平移的距离;
(3)在(2)的条件下,若三角形ABC的周长为25,求四边形ABFD的周长.
【解答】解:(1)∵△ABC沿射线BC方向平移得到△DEF,
∴AC∥DF,AD∥BF,
∴∠ACB=∠DFE,∠ACB=∠DAC,
∴∠DFE=∠DAC=60°;
(2)由平移的性质可得BE=CF,
又∵BE=CE,
∴,
∴平移的距离为5;
(3)由平移的性质可得AD=BE=CF=5,DF=AC,
∴四边形ABFD的周长=AB+BC+CF+DF+AD=AB+BC+AC+2AD=25+2×5=35.
13.(2024 铜山区二模)算盘是我国优秀文化遗产.它以排列成串的算珠作为计算工具,中间横梁把算珠分为上、下两部分,每个上珠代表5,每个下珠代表1.如图,小华在百位拨了一颗上珠和一颗下珠,然后对小明说:我将要拨的三位数,个位数字与十位数字之和是百位数字的2倍;个位数字减2等于十位数字加2,请求出这个三位数.
【解答】解:设个位数字为x,十位数字为y,
,
解得:,
则这个三位数为648.
14.(2024春 沛县月考)某体育用品商场销售A,B两款足球,售价和进价如表所示:
类型 进价/(元/个) 售价/(元/个)
A款 m 120
B款 n 90
若该商场购进4个A款足球和11个B款足球需980元;购进2个A款足球和3个B款足球需340元.
(1)求m和n的值.
(2)某校在该商场一次性购买A款足球x个和B款足球y个,共消费3000元,那么该商场可获利多少元?
(3)为了提高销量,商场实施:“买足球送跳绳”的促销活动:“买1个A款足球送1根跳绳,买3个B款足球送2根跳绳”,每根跳绳的成本为10元,某日售卖出两款足球总计盈利600元,那么该日商场销售A,B两款足球各多少个(每款都有销售)?
【解答】解:(1)根据题意得:,
解得:,
∴m的值为80,n的值为60;
(2)根据题意得:120x+90y=3000,
∴40x+30y=1000,
∴(120﹣80)x+(90﹣60)y=40x+30y=1000,
答:该商场可获利1000元;
(3)设该日商场销售a个A款足球,3b个B款足球,
根据题意得:(120﹣80﹣10)a+(90×3﹣60×3﹣10×2)b=600,
∴,
又∵a,b均为正整数,
∴或,
∴或,
答:该日商场销售13个A款足球、9个B款足球或6个A款足球、18个B款足球.
15.(2024 泰兴市二模)某公司组织50名员工外出团建,有两种出行方案及对应费用如表:
方案类型 坐动车人数 坐飞机人数 总费用
方案一 10人 40人 24000元
方案二 15人 35人 23750元
根据表中信息,求动车和飞机票价分别是多少元?
【解答】解:设动车票价是x元,飞机票价是y元,
根据题意得:,
解得:.
答:动车票价是440元,飞机票价是490元.
16.(2024春 海门区期末)为了解决民工子女入学难的问题,我市建立了一套进城民工子女就学的保障机制,其中一项就是免交“借读费”.据统计,去年秋季有5000名民工子女进入主城区中小学学习,预测今年秋季进入主城区中小学学习的民工子女将比去年有所增加,其中小学增加20%,中学增加30%,这样今年秋季将新增1160名民工子女在主城区中小学学习.
(1)如果按小学每年收“借读费”500元、中学每年收“借读费”1000元计算,求今年秋季新增的1160名中小学生共免收多少“借读费”;
(2)如果小学每40名学生配备2名教师,中学每40名学生配备3名教师,按今年秋季入学后,民工子女在主城区中小学就读的学生人数计算,一共需配备多少名中小学教师?
【解答】解:(1)设去年秋季有x名民工子女进入主城区小学学习,y名民工子女进入主城区中学学习,
根据题意得:,
解得:,
∴500×20%x+1000×30%y=500×20%×3400+1000×30%×1600=820000(元).
答:今年秋季新增的1160名中小学生共免收820000元“借读费”;
(2)根据题意得:3400×(1+1+20%)÷40×2+1600×(1+1+30%)÷40×3
=7480÷40×2+3680÷40×3
=374+276
=650(名).
答:按今年秋季入学后,民工子女在主城区中小学就读的学生人数计算,一共需配备650名中小学教师.
17.(2024春 南京期末)某校计划创建大小图书角共20个,现有图书3200册,其中每个小图书角需图书100册,每个大图书角需图书250册,问该校创建的大小图书角分别有多少个?
(1)小亮根据题意,列出方程组,请分别指出未知数x,y表示的意义:x表示 大图书角所需的图书册数 ,y表示 小图书角所需的图书册数 .
(2)小丽“设该校创建的大图书角m个,小图书角n个”,请按照小丽的思路列出方程组,并求m,n的值.
【解答】解:(1)x表示大图书角所需的图书册数,y表示小图书角所需的图书册数,
故答案为:大图书角所需的图书册数,小图书角所需的图书册数;
(2)由题意得:,
解得:,
答:m=8,n=12.
18.(2024春 丹阳市期末)【定义】我们把关于x、y的两个二元一次方程ax+by=c与bx+ay=c(a≠b)叫作“对称二元一次方程”,二元一次方程组叫做关于x、y的“对称二元一次方程组”.例如:2x+y=3与x+2y=3是“对称二元一次方程”,二元一次方程组叫做关于x、y的“对称二元一次方程组”.
【理解】
(1)方程2x﹣3y=5的“对称二元一次方程”是 ﹣3x+2y=5 ;
(2)若关于x、y的方程组为“对称二元一次方程组”,则a= 2 ,b= ﹣1 ;
【探究】
(3)解下列方程组(直接写出方程组的解):
①的解为 ;
②的解为 ;
③的解为 ;
(4)根据你的发现,直接写出方程组的解为 ;
【拓展】
(5)若关于x、y的方程组的解是,那么关于x、y的方程组的解为 .
【解答】解:(1)由题意,∵关于x、y的两个二元一次方程ax+by=c与bx+ay=c(a≠b)叫作“对称二元一次方程”,
∴方程2x﹣3y=5的“对称二元一次方程”是﹣3x+2y=5.
故答案为:﹣3x+2y=5.
(2)由题意,∵关于x、y的方程组为“对称二元一次方程组”,
∴.
∴.
故答案为:2,﹣1.
(3)①∵,
∴5x+5y=20,则x+y=4.
∴(2x+3y)﹣(2x+2y)=10﹣8.
∴y=2.
∴x=2.
∴原方程组的解为.
故答案为:.
②∵,
∴7x+7y=﹣14,则x+y=﹣2.
∴(3x+4y)﹣(3x+3y)=﹣7﹣(﹣6).
∴y=﹣1.
∴x=﹣1.
∴原方程组的解为.
故答案为:.
③∵,
∴﹣3x﹣3y=﹣12,则x+y=4.
∴(2x﹣5y)﹣(2x+2y)=﹣6﹣8.
∴﹣7y=﹣14,则y=2.
∴x=2.
∴原方程组的解为.
故答案为:.
(4)由题意,可以发现,方程组的解为.
∴的解为.
故答案为:.
(5)由题意,∵,
∴.
又∵关于x、y的方程组的解是,
∴,即.
∴方程组的解为.
故答案为:.
19.(2024春 高新区校级月考)某工厂计划生产A、B两种产品共10件,其生产成本和利润如表:
A种产品 B种产品
成本(万元/件) 2 5
利润(万元/件) 1 3
(1)若工厂计划获利14万元,问A、B两种产品应分别生产多少件?
(2)若工厂计划投入资金不多于44万元,且获利多于20万元,问工厂有哪几种生产方案?
(3)在(2)的条件下,哪种生产方案获利最大?并求出最大利润.
【解答】解:(1)设A种产品应生产x件,则B种产品应生产(10﹣x)件,
由题意,x+3(10﹣x)=14,
解得x=8,
∴10﹣x=2,
∴A种产品应生产8件,B种产品应生产2件.
(2)设A种产品应生产m件,则B种产品应生产(10﹣m)件,
由题意得,
解这个不等式组,得2≤m<5,
∵m为正整数,m可以取2或3或4;
∴生产方案有3种:
①生产A种产品2件,B种产品8件;
②生产A种产品3件,B种产品7件.
③生产A种产品4件,B种产品6件.
(3)设总利润为y万元,生产A种产品x件,则生产B种产品(10﹣x)件,
则利润y=x+3(10﹣x)=﹣2x+30,
则y随x的增大而减小,即可得,A产品生产越少,获利越大,
所以当生产A种产品2件,B种产品8件时可获得最大利润,其最大利润为2×1+8×3=26(万元).
20.(2024春 沛县月考)阅读下列材料:
[数学问题]已知x﹣y=2,且x>1,y<0,试确定x+y的取值范围.
[问题解决]∵x﹣y=2,∴x=y+2.
又∵x>1,
∴y+2>1,∴y>﹣1.
又∵y<0,
∴﹣1<y<0.①
同理得:1<x<2.②
由①+②得:﹣1+1<x+y<0+2.
即:0<x+y<2.
[类比探究]
(1)在数学问题中的条件下,x+2y的取值范围是 ﹣1<x+2y<2 .
(2)已知x﹣y=5,且x>2,y<0,
①求y的取值范围.
②求x+2y的取值范围.
(3)已知y≥1,x<﹣1,若x+y=a(a>0),直接写出x﹣2y的取值范围(用含a的代数式表示).
【解答】解:(1)∵﹣1<y<0,
∴﹣2<2y<0,
∵1<x<2,
∴﹣1<x+2y<2;
故答案为:﹣1<x+2y<2;
(2)①∵x﹣y=5,
∴x=5+y,
又∵x>2,
∴5+y>2,
∴y>﹣3,
又∵y<0,
∴﹣3<y<0,
②∵x﹣y=5,
∴y=x﹣5,
又∵y<0,
∴x﹣5<0,
∴x<5,
∴2<x<5,
∵﹣3<y<0,
∴﹣6<2y<0,
∴﹣4<x+2y<5.
(3)∵x+y=a,
∴x=a﹣y,
又∵x<﹣1,
∴a﹣y<﹣1,
∴y>1+a,
又∵y≥1,a>0,
∴y>1+a,
∴﹣2y<﹣2﹣2a
同理得:x<﹣1,
∴x﹣2y<﹣3﹣2a,
∴x﹣2y的取值范围是x﹣2y<﹣3﹣2a.
21.(2024春 亭湖区校级期末)如图,①AB∥CD,②BE平分∠ABD,③DE平分∠BDC,④∠1+∠2=90°.(1)若以①②③为条件,④为结论组成一个命题,则这个命题是 真 (“真”或“假”)命题;
(2)若(1)为真命题,证明(1)中的结论:若(1)为假命题,请举出反例.
【解答】解:(1)即若以①②③为条件,④为结论组成一个命题,则这个命题是真命题,
故答案为:真;
(2)∵AB∥CD,
∴∠ABD+∠CDB=180°,
∵BE平分∠ABD,
∴∠ABE=∠1,
∵DE平分∠BDC,
∴∠CDE=∠2,
∵∠ABD+∠CDB=180°,
∴∠ABE+∠1+∠CDE+∠2=180°,
∠1+∠1+∠2+∠2=180°,
2(∠1+∠2)=180°,
∠1+∠2=90°.
22.(2024春 睢宁县期末)如图,从①∠1=∠2②∠C=∠D③∠A=∠F三个条件中选出两个作为已知条件,另一个作为结论可以组成3个命题.
(1)这三个命题中,真命题的个数为 3 ;
(2)选择一个真命题,并且证明,(要求写出每一步的依据)
如图,已知 ①∠1=∠2,②∠C=∠D ,
求证: ③∠A=∠F
证明: ∵∠1=∠2,∠1=∠3(已知),
∴∠3=∠2(等量代换),
∴DB∥EC(同位角相等,两直线平行),
∴∠D=∠4(两直线平行,同位角相等),
∵∠C=∠D(已知),
∴∠4=∠C(等量代换),
∴DF∥AC(内错角相等,两直线平行),
∴∠A=∠F(两直线平行,内错角相等).
【解答】解:(1)由 ①②,得 ③;由①③,得②;由②③,得①;均正确,
故答案为3
(2)已知∠1=∠2,∠C=∠D,求证:∠A=∠F,
证明:如图所示:
∵∠1=∠2,∠1=∠3(已知),
∴∠3=∠2(等量代换),
∴DB∥EC(同位角相等,两直线平行),
∴∠D=∠4(两直线平行,同位角相等),
∵∠C=∠D(已知),
∴∠4=∠C(等量代换),
∴DF∥AC(内错角相等,两直线平行),
∴∠A=∠F(两直线平行,内错角相等).
证明步骤同上.
故答案为:①∠1=∠2,②∠C=∠D;∠A=∠F;
21世纪教育网 www.21cnjy.com 精品试卷·第 2 页 (共 2 页)
21世纪教育网(www.21cnjy.com)
【江苏省各地区期末真题汇编】热点题型分类突破:解答题-2024-2024学年数学七年级下册苏科版(2024)
1.(2024春 赣榆区期末)若am=an(a>0且a≠1,m,n是正整数),则m=n.试利用该结论求x的值:3×9x×81=321.
2.(2024春 徐州期末)在幂的运算中规定:若ax=ay(a>0且a≠1,x,y是正整数),则x=y.
(1)如果2×4x=219,求x的值;
(2)如果5x+2﹣5x+1=500,求x的值.
3.(2024春 海陵区期末)比较两个底数大于1的正数幂的大小,可以在底数(或指数)相同的情况下,比较指数(或底数)的大小,如:25>23,55>45.
(1)比较254,1253的大小.
(2)比较3555,4444,5333的大小.
4.(2024春 宜兴市期末)如果ac=b,那么我们规定(a,b)=c,例如:因为23=8,所以(2,8)=3
(1)根据上述规定,填空:
(3,27)= ,(4,1)= (2,0.25)= ;
(2)记(3,5)=a,(3,6)=b,(3,30)=c.求证:a+b=c.
5.(2024春 灌南县期末)如图,某市有一块长为(3a+b)米,宽为(2a+b)米的长方形地块,规划部门计划将阴影部分进行绿化,中间将修建一座雕像.
(1)求绿化的面积是多少平方米?(用代数式表示)
(2)求出当a=3,b=2时的绿化面积.
6.(2024春 海陵区期末)从边长为a的正方形中剪掉一个边长为b的正方形(如图1),然后将剩余部分拼成一个长方形(如图2).
(1)上述操作可以得到一个公式: .
(2)利用你得到的公式,计算:20242﹣2023×2024;
(3)计算:3(22+1)(24+1)(28+1)(216+1).
7.(2023秋 启东市月考)将边长为x的小正方形ABCD和边长为y的大正方形CEFG按如图所示放置,其中点D在边CE上.
(1)若x+y=10,y2﹣x2=20,求y﹣x的值;
(2)连接AG,EG,若x+y=8,xy=14,求阴影部分的面积.
8.(2024春 高新区月考)【知识回顾】
我们在学习代数式求值时,遇到这样一类题:代数式ax﹣y+6+3x一5y﹣1的值与x的取值无关,求a的值.
通常的解题思路是:把x、y看作字母,a看作系数,合并同类项.因为代数式的值与x的取值无关,所以含x项的系数为0.
具体解题过程是:原式(a+3)x﹣6y+5,
∵代数式的值与x的取值无关,
∴a+3=0,解a=﹣3.
【理解应用】
(1)若关于x的代数式mx﹣4x+3的值与x的取值无关,则m值为 .
(2)已知A=(2x+1)(x﹣2),B=x(m﹣x),且A+2B的值与x的取值无关,求m的值.
【能力提升】
(3)7张如图1的小长方形,长为a,宽为b,按照图2方式不重叠地放在大长方形ABCD内,大长方形中未被覆盖的两个部分都是长方形.设右上角的面积为S1,左下角的面积为S2,当AB的长变化时,S1﹣S2的值始终保持不变,求a与b的等量关系.
9.(2024春 苏州校级期末)如图,将△ABC沿BC方向平移,得到△DEF.
(1)若∠B=80°,∠F=32°,求∠A的度数;
(2)若BC=5,EC=3,求CF的长.
10.(2024春 东海县期末)△ABC在平面直角坐标系中,如图所示,A(1,1),B(4,2),C(3,4).
(1)请画出△ABC关于原点O对称的△A1B1C1;
(2)将△A1B1C1向右平移4个单位得到△A2B2C2,请画出△A2B2C2;
(3)线段AC与A2C2关于点D成中心对称,请直接写出点D的坐标.
11.(2024春 赣榆区期末)如图,把△ABC绕着A点按逆时针方向旋转40°得到△AEF,EF与AC交于点D点,若∠ADF=90°,求∠C的度数.
12.(2024春 锡山区期末)如图,将三角形ABC沿射线BC方向平移得到三角形DEF,点A,B,C的对应点分别是点D,E,F.
(1)若∠DAC=60°,求∠DFE的度数;
(2)若BF=15,BE=CE,求平移的距离;
(3)在(2)的条件下,若三角形ABC的周长为25,求四边形ABFD的周长.
13.(2024 铜山区二模)算盘是我国优秀文化遗产.它以排列成串的算珠作为计算工具,中间横梁把算珠分为上、下两部分,每个上珠代表5,每个下珠代表1.如图,小华在百位拨了一颗上珠和一颗下珠,然后对小明说:我将要拨的三位数,个位数字与十位数字之和是百位数字的2倍;个位数字减2等于十位数字加2,请求出这个三位数.
14.(2024春 沛县月考)某体育用品商场销售A,B两款足球,售价和进价如表所示:
类型 进价/(元/个) 售价/(元/个)
A款 m 120
B款 n 90
若该商场购进4个A款足球和11个B款足球需980元;购进2个A款足球和3个B款足球需340元.
(1)求m和n的值.
(2)某校在该商场一次性购买A款足球x个和B款足球y个,共消费3000元,那么该商场可获利多少元?
(3)为了提高销量,商场实施:“买足球送跳绳”的促销活动:“买1个A款足球送1根跳绳,买3个B款足球送2根跳绳”,每根跳绳的成本为10元,某日售卖出两款足球总计盈利600元,那么该日商场销售A,B两款足球各多少个(每款都有销售)?
15.(2024 泰兴市二模)某公司组织50名员工外出团建,有两种出行方案及对应费用如表:
方案类型 坐动车人数 坐飞机人数 总费用
方案一 10人 40人 24000元
方案二 15人 35人 23750元
根据表中信息,求动车和飞机票价分别是多少元?
16.(2024春 海门区期末)为了解决民工子女入学难的问题,我市建立了一套进城民工子女就学的保障机制,其中一项就是免交“借读费”.据统计,去年秋季有5000名民工子女进入主城区中小学学习,预测今年秋季进入主城区中小学学习的民工子女将比去年有所增加,其中小学增加20%,中学增加30%,这样今年秋季将新增1160名民工子女在主城区中小学学习.
(1)如果按小学每年收“借读费”500元、中学每年收“借读费”1000元计算,求今年秋季新增的1160名中小学生共免收多少“借读费”;
(2)如果小学每40名学生配备2名教师,中学每40名学生配备3名教师,按今年秋季入学后,民工子女在主城区中小学就读的学生人数计算,一共需配备多少名中小学教师?
17.(2024春 南京期末)某校计划创建大小图书角共20个,现有图书3200册,其中每个小图书角需图书100册,每个大图书角需图书250册,问该校创建的大小图书角分别有多少个?
(1)小亮根据题意,列出方程组,请分别指出未知数x,y表示的意义:x表示 ,y表示 .
(2)小丽“设该校创建的大图书角m个,小图书角n个”,请按照小丽的思路列出方程组,并求m,n的值.
18.(2024春 丹阳市期末)【定义】我们把关于x、y的两个二元一次方程ax+by=c与bx+ay=c(a≠b)叫作“对称二元一次方程”,二元一次方程组叫做关于x、y的“对称二元一次方程组”.例如:2x+y=3与x+2y=3是“对称二元一次方程”,二元一次方程组叫做关于x、y的“对称二元一次方程组”.
【理解】
(1)方程2x﹣3y=5的“对称二元一次方程”是 ;
(2)若关于x、y的方程组为“对称二元一次方程组”,则a= ,b= ;
【探究】
(3)解下列方程组(直接写出方程组的解):
①的解为 ;
②的解为 ;
③的解为 ;
(4)根据你的发现,直接写出方程组的解为 ;
【拓展】
(5)若关于x、y的方程组的解是,那么关于x、y的方程组的解为 .
19.(2024春 高新区校级月考)某工厂计划生产A、B两种产品共10件,其生产成本和利润如表:
A种产品 B种产品
成本(万元/件) 2 5
利润(万元/件) 1 3
(1)若工厂计划获利14万元,问A、B两种产品应分别生产多少件?
(2)若工厂计划投入资金不多于44万元,且获利多于20万元,问工厂有哪几种生产方案?
(3)在(2)的条件下,哪种生产方案获利最大?并求出最大利润.
20.(2024春 沛县月考)阅读下列材料:
[数学问题]已知x﹣y=2,且x>1,y<0,试确定x+y的取值范围.
[问题解决]∵x﹣y=2,∴x=y+2.
又∵x>1,
∴y+2>1,∴y>﹣1.
又∵y<0,
∴﹣1<y<0.①
同理得:1<x<2.②
由①+②得:﹣1+1<x+y<0+2.
即:0<x+y<2.
[类比探究]
(1)在数学问题中的条件下,x+2y的取值范围是 .
(2)已知x﹣y=5,且x>2,y<0,
①求y的取值范围.
②求x+2y的取值范围.
(3)已知y≥1,x<﹣1,若x+y=a(a>0),直接写出x﹣2y的取值范围(用含a的代数式表示).
21.(2024春 亭湖区校级期末)如图,①AB∥CD,②BE平分∠ABD,③DE平分∠BDC,④∠1+∠2=90°.(1)若以①②③为条件,④为结论组成一个命题,则这个命题是 (“真”或“假”)命题;
(2)若(1)为真命题,证明(1)中的结论:若(1)为假命题,请举出反例.
22.(2024春 睢宁县期末)如图,从①∠1=∠2②∠C=∠D③∠A=∠F三个条件中选出两个作为已知条件,另一个作为结论可以组成3个命题.
(1)这三个命题中,真命题的个数为 ;
(2)选择一个真命题,并且证明,(要求写出每一步的依据)
如图,已知 ,
求证:
证明:
【江苏省各地区期末真题汇编】热点题型分类突破:解答题-2024-2024学年数学七年级下册苏科版(2024)
参考答案与试题解析
一.解答题(共22小题)
1.(2024春 赣榆区期末)若am=an(a>0且a≠1,m,n是正整数),则m=n.试利用该结论求x的值:3×9x×81=321.
【解答】解:∵3×9x×81=3×32x×34=31+2x+4=32x+5,
∴2x+5=21,
∴x=8.
2.(2024春 徐州期末)在幂的运算中规定:若ax=ay(a>0且a≠1,x,y是正整数),则x=y.
(1)如果2×4x=219,求x的值;
(2)如果5x+2﹣5x+1=500,求x的值.
【解答】解:(1)由条件可得2×(22)x=219,
∴2×22x=219,22x+1=219,
∴2x+1=19,
解得:x=9;
(2)由条件可知5x+1(5﹣1)=53×4,
∴5x+1=53,
∴x+1=3,
解得:x=2.
3.(2024春 海陵区期末)比较两个底数大于1的正数幂的大小,可以在底数(或指数)相同的情况下,比较指数(或底数)的大小,如:25>23,55>45.
(1)比较254,1253的大小.
(2)比较3555,4444,5333的大小.
【解答】解:(1)254=(52)4=58,
1253=(53)3=59,
∵58<59,
∴254<1253.
(2)3555=(35)111=243111,
4444=(44)111=256111,
5333=(53)111=125111.
∵256111>243111>125111,
∴4444>3555>5333.
4.(2024春 宜兴市期末)如果ac=b,那么我们规定(a,b)=c,例如:因为23=8,所以(2,8)=3
(1)根据上述规定,填空:
(3,27)= 3 ,(4,1)= 0 (2,0.25)= ﹣2 ;
(2)记(3,5)=a,(3,6)=b,(3,30)=c.求证:a+b=c.
【解答】解:(1)(3,27)=3,(4,1)=0,(2,0.25)=﹣2,
故答案为:3,0,﹣2;
(2)证明:∵(3,5)=a,(3,6)=b,(3,30)=c,
∴3a=5,3b=6,3c=30,
∴3a×3b=30,
∴3a×3b=3c,
∴a+b=c.
5.(2024春 灌南县期末)如图,某市有一块长为(3a+b)米,宽为(2a+b)米的长方形地块,规划部门计划将阴影部分进行绿化,中间将修建一座雕像.
(1)求绿化的面积是多少平方米?(用代数式表示)
(2)求出当a=3,b=2时的绿化面积.
【解答】解:(1)阴影部分的面积=(3a+b)(2a+b)﹣(a+b)2
=6a2+5ab+b2﹣a2﹣2ab﹣b2
=5a2+3ab;
(2)当a=3,b=2时,原式=5×32+3×3×2=63(平方米).
6.(2024春 海陵区期末)从边长为a的正方形中剪掉一个边长为b的正方形(如图1),然后将剩余部分拼成一个长方形(如图2).
(1)上述操作可以得到一个公式: a2﹣b2=(a+b)(a﹣b) .
(2)利用你得到的公式,计算:20242﹣2023×2024;
(3)计算:3(22+1)(24+1)(28+1)(216+1).
【解答】解:(1)图1中阴影部分可以看作两个正方形的面积差,即a2﹣b2,拼成的图2是长为a+b,宽为a﹣b的长方形,因此面积为(a+b)(a﹣b),
所以有a2﹣b2=(a+b)(a﹣b),
故答案为:a2﹣b2=(a+b)(a﹣b);
(2)原式=20242﹣(2024﹣1)(2024+1)
=20242﹣20242+1
=1;
(3)原式=(22﹣1)(22+1)(24+1)(28+1)(216+1)
=(24﹣1)(24+1)(28+1)(216+1)
=(28﹣1)(28+1)(216+1)
=(216﹣1)(216+1)
=232﹣1.
7.(2023秋 启东市月考)将边长为x的小正方形ABCD和边长为y的大正方形CEFG按如图所示放置,其中点D在边CE上.
(1)若x+y=10,y2﹣x2=20,求y﹣x的值;
(2)连接AG,EG,若x+y=8,xy=14,求阴影部分的面积.
【解答】解:(1)∵y2﹣x2=20,即(y+x)(y﹣x)=20,而x+y=10,
∴y﹣x=2,
答:y﹣x的值为2;
(2)由题意得,
S阴影部分=S正方形ABCD+S正方形CEFG﹣S△ABG﹣S△EFG
=x2+y2x(x+y)y2
x2xyy2
[(x+y)2﹣2xy]xy
当x+y=8,xy=14时,
原式(64﹣28)14
=18﹣7
=11,
答:阴影部分的面积是11.
8.(2024春 高新区月考)【知识回顾】
我们在学习代数式求值时,遇到这样一类题:代数式ax﹣y+6+3x一5y﹣1的值与x的取值无关,求a的值.
通常的解题思路是:把x、y看作字母,a看作系数,合并同类项.因为代数式的值与x的取值无关,所以含x项的系数为0.
具体解题过程是:原式(a+3)x﹣6y+5,
∵代数式的值与x的取值无关,
∴a+3=0,解a=﹣3.
【理解应用】
(1)若关于x的代数式mx﹣4x+3的值与x的取值无关,则m值为 4 .
(2)已知A=(2x+1)(x﹣2),B=x(m﹣x),且A+2B的值与x的取值无关,求m的值.
【能力提升】
(3)7张如图1的小长方形,长为a,宽为b,按照图2方式不重叠地放在大长方形ABCD内,大长方形中未被覆盖的两个部分都是长方形.设右上角的面积为S1,左下角的面积为S2,当AB的长变化时,S1﹣S2的值始终保持不变,求a与b的等量关系.
【解答】解:(1)mx﹣4x+3
=(m﹣4)x+3,
∵关于x的代数式mx﹣4x+3的值与x的取值无关,
∴m﹣4=0,
解得:m=4,
故答案为:4;
(2)∵A=(2x+1)(x﹣2)
=2x2﹣4x+x﹣2
=2x2﹣3x﹣2,
2B=2x(m﹣x)
=2mx﹣2x2,
∴A+2B=2x2﹣3x﹣2+2mx﹣2x2
=2x2﹣2x2+2mx﹣3x﹣2
=2mx﹣3x﹣2
=(2m﹣3)x﹣2,
∵A+2B的值与x无关,
∴2m﹣3=0,
解得:;
(3)设AB=x,由图可知S1=a(x﹣3b),S2=2b(x﹣2a),
∴S1﹣S2
=a(x﹣3b)﹣2b(x﹣2a)
=ax﹣3ab﹣2bx+4ab
=(a﹣2b)x+ab,
∵当AB的长变化时,S1﹣S2的值始终保持不变,
∴S1﹣S2取值与x无关,
∴a﹣2b=0,
∴a=2b.
9.(2024春 苏州校级期末)如图,将△ABC沿BC方向平移,得到△DEF.
(1)若∠B=80°,∠F=32°,求∠A的度数;
(2)若BC=5,EC=3,求CF的长.
【解答】解:(1)因为△DEF由△ABC沿BC方向平移得到,
所以∠2=∠F=32°.
又因为∠B=80°,
所以∠A=180°﹣32°﹣80°=68°.
(2)由平移可知,
EF=BC,
所以EF﹣EC=BC﹣EC,
即CF=BE.
又因为BC=5,EC=3,
所以BE=BC﹣EC=5﹣3=2,
所以CF=BE=2.
10.(2024春 东海县期末)△ABC在平面直角坐标系中,如图所示,A(1,1),B(4,2),C(3,4).
(1)请画出△ABC关于原点O对称的△A1B1C1;
(2)将△A1B1C1向右平移4个单位得到△A2B2C2,请画出△A2B2C2;
(3)线段AC与A2C2关于点D成中心对称,请直接写出点D的坐标.
【解答】解:(1)如图,△A1B1C1即为所求.
(2)如图,△A2B2C2即为所求.
(3)连接AA2,CC2相交于点D,
∴点D的坐标为(2,0).
11.(2024春 赣榆区期末)如图,把△ABC绕着A点按逆时针方向旋转40°得到△AEF,EF与AC交于点D点,若∠ADF=90°,求∠C的度数.
【解答】解:∵把△ABC绕着A点按逆时针方向旋转40°得到△AEF,
∴∠C=∠F,∠DAF=40°,
而∠ADF=90°,
∴∠C=∠F=50°.
12.(2024春 锡山区期末)如图,将三角形ABC沿射线BC方向平移得到三角形DEF,点A,B,C的对应点分别是点D,E,F.
(1)若∠DAC=60°,求∠DFE的度数;
(2)若BF=15,BE=CE,求平移的距离;
(3)在(2)的条件下,若三角形ABC的周长为25,求四边形ABFD的周长.
【解答】解:(1)∵△ABC沿射线BC方向平移得到△DEF,
∴AC∥DF,AD∥BF,
∴∠ACB=∠DFE,∠ACB=∠DAC,
∴∠DFE=∠DAC=60°;
(2)由平移的性质可得BE=CF,
又∵BE=CE,
∴,
∴平移的距离为5;
(3)由平移的性质可得AD=BE=CF=5,DF=AC,
∴四边形ABFD的周长=AB+BC+CF+DF+AD=AB+BC+AC+2AD=25+2×5=35.
13.(2024 铜山区二模)算盘是我国优秀文化遗产.它以排列成串的算珠作为计算工具,中间横梁把算珠分为上、下两部分,每个上珠代表5,每个下珠代表1.如图,小华在百位拨了一颗上珠和一颗下珠,然后对小明说:我将要拨的三位数,个位数字与十位数字之和是百位数字的2倍;个位数字减2等于十位数字加2,请求出这个三位数.
【解答】解:设个位数字为x,十位数字为y,
,
解得:,
则这个三位数为648.
14.(2024春 沛县月考)某体育用品商场销售A,B两款足球,售价和进价如表所示:
类型 进价/(元/个) 售价/(元/个)
A款 m 120
B款 n 90
若该商场购进4个A款足球和11个B款足球需980元;购进2个A款足球和3个B款足球需340元.
(1)求m和n的值.
(2)某校在该商场一次性购买A款足球x个和B款足球y个,共消费3000元,那么该商场可获利多少元?
(3)为了提高销量,商场实施:“买足球送跳绳”的促销活动:“买1个A款足球送1根跳绳,买3个B款足球送2根跳绳”,每根跳绳的成本为10元,某日售卖出两款足球总计盈利600元,那么该日商场销售A,B两款足球各多少个(每款都有销售)?
【解答】解:(1)根据题意得:,
解得:,
∴m的值为80,n的值为60;
(2)根据题意得:120x+90y=3000,
∴40x+30y=1000,
∴(120﹣80)x+(90﹣60)y=40x+30y=1000,
答:该商场可获利1000元;
(3)设该日商场销售a个A款足球,3b个B款足球,
根据题意得:(120﹣80﹣10)a+(90×3﹣60×3﹣10×2)b=600,
∴,
又∵a,b均为正整数,
∴或,
∴或,
答:该日商场销售13个A款足球、9个B款足球或6个A款足球、18个B款足球.
15.(2024 泰兴市二模)某公司组织50名员工外出团建,有两种出行方案及对应费用如表:
方案类型 坐动车人数 坐飞机人数 总费用
方案一 10人 40人 24000元
方案二 15人 35人 23750元
根据表中信息,求动车和飞机票价分别是多少元?
【解答】解:设动车票价是x元,飞机票价是y元,
根据题意得:,
解得:.
答:动车票价是440元,飞机票价是490元.
16.(2024春 海门区期末)为了解决民工子女入学难的问题,我市建立了一套进城民工子女就学的保障机制,其中一项就是免交“借读费”.据统计,去年秋季有5000名民工子女进入主城区中小学学习,预测今年秋季进入主城区中小学学习的民工子女将比去年有所增加,其中小学增加20%,中学增加30%,这样今年秋季将新增1160名民工子女在主城区中小学学习.
(1)如果按小学每年收“借读费”500元、中学每年收“借读费”1000元计算,求今年秋季新增的1160名中小学生共免收多少“借读费”;
(2)如果小学每40名学生配备2名教师,中学每40名学生配备3名教师,按今年秋季入学后,民工子女在主城区中小学就读的学生人数计算,一共需配备多少名中小学教师?
【解答】解:(1)设去年秋季有x名民工子女进入主城区小学学习,y名民工子女进入主城区中学学习,
根据题意得:,
解得:,
∴500×20%x+1000×30%y=500×20%×3400+1000×30%×1600=820000(元).
答:今年秋季新增的1160名中小学生共免收820000元“借读费”;
(2)根据题意得:3400×(1+1+20%)÷40×2+1600×(1+1+30%)÷40×3
=7480÷40×2+3680÷40×3
=374+276
=650(名).
答:按今年秋季入学后,民工子女在主城区中小学就读的学生人数计算,一共需配备650名中小学教师.
17.(2024春 南京期末)某校计划创建大小图书角共20个,现有图书3200册,其中每个小图书角需图书100册,每个大图书角需图书250册,问该校创建的大小图书角分别有多少个?
(1)小亮根据题意,列出方程组,请分别指出未知数x,y表示的意义:x表示 大图书角所需的图书册数 ,y表示 小图书角所需的图书册数 .
(2)小丽“设该校创建的大图书角m个,小图书角n个”,请按照小丽的思路列出方程组,并求m,n的值.
【解答】解:(1)x表示大图书角所需的图书册数,y表示小图书角所需的图书册数,
故答案为:大图书角所需的图书册数,小图书角所需的图书册数;
(2)由题意得:,
解得:,
答:m=8,n=12.
18.(2024春 丹阳市期末)【定义】我们把关于x、y的两个二元一次方程ax+by=c与bx+ay=c(a≠b)叫作“对称二元一次方程”,二元一次方程组叫做关于x、y的“对称二元一次方程组”.例如:2x+y=3与x+2y=3是“对称二元一次方程”,二元一次方程组叫做关于x、y的“对称二元一次方程组”.
【理解】
(1)方程2x﹣3y=5的“对称二元一次方程”是 ﹣3x+2y=5 ;
(2)若关于x、y的方程组为“对称二元一次方程组”,则a= 2 ,b= ﹣1 ;
【探究】
(3)解下列方程组(直接写出方程组的解):
①的解为 ;
②的解为 ;
③的解为 ;
(4)根据你的发现,直接写出方程组的解为 ;
【拓展】
(5)若关于x、y的方程组的解是,那么关于x、y的方程组的解为 .
【解答】解:(1)由题意,∵关于x、y的两个二元一次方程ax+by=c与bx+ay=c(a≠b)叫作“对称二元一次方程”,
∴方程2x﹣3y=5的“对称二元一次方程”是﹣3x+2y=5.
故答案为:﹣3x+2y=5.
(2)由题意,∵关于x、y的方程组为“对称二元一次方程组”,
∴.
∴.
故答案为:2,﹣1.
(3)①∵,
∴5x+5y=20,则x+y=4.
∴(2x+3y)﹣(2x+2y)=10﹣8.
∴y=2.
∴x=2.
∴原方程组的解为.
故答案为:.
②∵,
∴7x+7y=﹣14,则x+y=﹣2.
∴(3x+4y)﹣(3x+3y)=﹣7﹣(﹣6).
∴y=﹣1.
∴x=﹣1.
∴原方程组的解为.
故答案为:.
③∵,
∴﹣3x﹣3y=﹣12,则x+y=4.
∴(2x﹣5y)﹣(2x+2y)=﹣6﹣8.
∴﹣7y=﹣14,则y=2.
∴x=2.
∴原方程组的解为.
故答案为:.
(4)由题意,可以发现,方程组的解为.
∴的解为.
故答案为:.
(5)由题意,∵,
∴.
又∵关于x、y的方程组的解是,
∴,即.
∴方程组的解为.
故答案为:.
19.(2024春 高新区校级月考)某工厂计划生产A、B两种产品共10件,其生产成本和利润如表:
A种产品 B种产品
成本(万元/件) 2 5
利润(万元/件) 1 3
(1)若工厂计划获利14万元,问A、B两种产品应分别生产多少件?
(2)若工厂计划投入资金不多于44万元,且获利多于20万元,问工厂有哪几种生产方案?
(3)在(2)的条件下,哪种生产方案获利最大?并求出最大利润.
【解答】解:(1)设A种产品应生产x件,则B种产品应生产(10﹣x)件,
由题意,x+3(10﹣x)=14,
解得x=8,
∴10﹣x=2,
∴A种产品应生产8件,B种产品应生产2件.
(2)设A种产品应生产m件,则B种产品应生产(10﹣m)件,
由题意得,
解这个不等式组,得2≤m<5,
∵m为正整数,m可以取2或3或4;
∴生产方案有3种:
①生产A种产品2件,B种产品8件;
②生产A种产品3件,B种产品7件.
③生产A种产品4件,B种产品6件.
(3)设总利润为y万元,生产A种产品x件,则生产B种产品(10﹣x)件,
则利润y=x+3(10﹣x)=﹣2x+30,
则y随x的增大而减小,即可得,A产品生产越少,获利越大,
所以当生产A种产品2件,B种产品8件时可获得最大利润,其最大利润为2×1+8×3=26(万元).
20.(2024春 沛县月考)阅读下列材料:
[数学问题]已知x﹣y=2,且x>1,y<0,试确定x+y的取值范围.
[问题解决]∵x﹣y=2,∴x=y+2.
又∵x>1,
∴y+2>1,∴y>﹣1.
又∵y<0,
∴﹣1<y<0.①
同理得:1<x<2.②
由①+②得:﹣1+1<x+y<0+2.
即:0<x+y<2.
[类比探究]
(1)在数学问题中的条件下,x+2y的取值范围是 ﹣1<x+2y<2 .
(2)已知x﹣y=5,且x>2,y<0,
①求y的取值范围.
②求x+2y的取值范围.
(3)已知y≥1,x<﹣1,若x+y=a(a>0),直接写出x﹣2y的取值范围(用含a的代数式表示).
【解答】解:(1)∵﹣1<y<0,
∴﹣2<2y<0,
∵1<x<2,
∴﹣1<x+2y<2;
故答案为:﹣1<x+2y<2;
(2)①∵x﹣y=5,
∴x=5+y,
又∵x>2,
∴5+y>2,
∴y>﹣3,
又∵y<0,
∴﹣3<y<0,
②∵x﹣y=5,
∴y=x﹣5,
又∵y<0,
∴x﹣5<0,
∴x<5,
∴2<x<5,
∵﹣3<y<0,
∴﹣6<2y<0,
∴﹣4<x+2y<5.
(3)∵x+y=a,
∴x=a﹣y,
又∵x<﹣1,
∴a﹣y<﹣1,
∴y>1+a,
又∵y≥1,a>0,
∴y>1+a,
∴﹣2y<﹣2﹣2a
同理得:x<﹣1,
∴x﹣2y<﹣3﹣2a,
∴x﹣2y的取值范围是x﹣2y<﹣3﹣2a.
21.(2024春 亭湖区校级期末)如图,①AB∥CD,②BE平分∠ABD,③DE平分∠BDC,④∠1+∠2=90°.(1)若以①②③为条件,④为结论组成一个命题,则这个命题是 真 (“真”或“假”)命题;
(2)若(1)为真命题,证明(1)中的结论:若(1)为假命题,请举出反例.
【解答】解:(1)即若以①②③为条件,④为结论组成一个命题,则这个命题是真命题,
故答案为:真;
(2)∵AB∥CD,
∴∠ABD+∠CDB=180°,
∵BE平分∠ABD,
∴∠ABE=∠1,
∵DE平分∠BDC,
∴∠CDE=∠2,
∵∠ABD+∠CDB=180°,
∴∠ABE+∠1+∠CDE+∠2=180°,
∠1+∠1+∠2+∠2=180°,
2(∠1+∠2)=180°,
∠1+∠2=90°.
22.(2024春 睢宁县期末)如图,从①∠1=∠2②∠C=∠D③∠A=∠F三个条件中选出两个作为已知条件,另一个作为结论可以组成3个命题.
(1)这三个命题中,真命题的个数为 3 ;
(2)选择一个真命题,并且证明,(要求写出每一步的依据)
如图,已知 ①∠1=∠2,②∠C=∠D ,
求证: ③∠A=∠F
证明: ∵∠1=∠2,∠1=∠3(已知),
∴∠3=∠2(等量代换),
∴DB∥EC(同位角相等,两直线平行),
∴∠D=∠4(两直线平行,同位角相等),
∵∠C=∠D(已知),
∴∠4=∠C(等量代换),
∴DF∥AC(内错角相等,两直线平行),
∴∠A=∠F(两直线平行,内错角相等).
【解答】解:(1)由 ①②,得 ③;由①③,得②;由②③,得①;均正确,
故答案为3
(2)已知∠1=∠2,∠C=∠D,求证:∠A=∠F,
证明:如图所示:
∵∠1=∠2,∠1=∠3(已知),
∴∠3=∠2(等量代换),
∴DB∥EC(同位角相等,两直线平行),
∴∠D=∠4(两直线平行,同位角相等),
∵∠C=∠D(已知),
∴∠4=∠C(等量代换),
∴DF∥AC(内错角相等,两直线平行),
∴∠A=∠F(两直线平行,内错角相等).
证明步骤同上.
故答案为:①∠1=∠2,②∠C=∠D;∠A=∠F;
21世纪教育网 www.21cnjy.com 精品试卷·第 2 页 (共 2 页)
21世纪教育网(www.21cnjy.com)
同课章节目录
