【江苏省考前冲刺特训】8+3+3模拟真题练习(三)-2025年高考数学(含解析)
文档属性
| 名称 | 【江苏省考前冲刺特训】8+3+3模拟真题练习(三)-2025年高考数学(含解析) |  | |
| 格式 | docx | ||
| 文件大小 | 308.9KB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 通用版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2025-05-30 15:26:36 | ||
图片预览




文档简介
中小学教育资源及组卷应用平台
【江苏省考前冲刺特训】8+3+3模拟真题练习(三)-2025年高考数学
一.选择题(共8小题)
1.(2025 九龙坡区校级一模)设集合A={x|x2﹣x﹣2≤0},B={x|y=lnx},则A∪B=( )
A.(0,2] B.[﹣1,+∞) C.(0,2) D.[﹣1,2]
2.(2025 山东校级一模)已知两个单位向量满足,则( )
A.0 B. C.1 D.2
3.(2025 四川模拟)赵爽是我国古代数学家,他为《周髀算经》一书作序时,介绍了“勾股圆方图”,亦称“赵爽弦图”(以弦为边长得到的正方形由4个全等的直角三角形再加上中间的一个小正方形组成).如图的“赵爽弦图”中小正方形的面积为49,大正方形的面积为169,直角三角形中较大的锐角为α,则sin2α=( )
A. B. C. D.
4.(2025 张家口三模)若(2﹣x)n的展开式中x2的系数为240,则n=( )
A.4 B.5 C.6 D.8
5.(2025 临泉县校级三模)已知线段AB=5,AC=4,D为线段AB上一点,CD=2,记AB与AC的夹角为θ,若对于某个范围内任意固定的θ,总存在两个不同的△ACD符合题意,则cosθ的取值范围是( )
A. B. C. D.
6.(2025 沙坪坝区校级模拟)已知三棱柱ABC﹣A1B1C1的体积为1,E,F分别是棱BC,CA的中点,则以A,B,B1,A1,E,F为顶点的五面体的体积为( )
A. B. C. D.
7.(2025 龙华区校级模拟)已知F1,F2分别为双曲线C:的左、右焦点,A为双曲线C上的一点,且AF1⊥F1F2,|AF1|=3,,则双曲线C的离心率为( )
A. B. C. D.3
8.(2025 湖北模拟)通信工程中常用n元数组(a1,a2,a3,…,an)表示信息,其中a1=0或1,且i,n∈N*.设u=(a1,a2,a3,…,an),v=(b1,b2,…,bn),d(u,v)表示u和v中相对应的元素不同的个数.如u=(1,0,0,1),v=(1,1,1,0),则d(u,v)=3.若u=(1,0,1,0,1,0),则使得d(u,v)=2的6元数组v的个数为( )
A.15 B.20 C.30 D.40
二.多选题(共3小题)
(多选)9.(2025 罗湖区校级模拟)如果存在正实数a,使得f(x+a)为奇函数,f(x﹣a)为偶函数,我们称函数f(x)为”和谐函数”.则下列四个函数,是“和谐函数”的是( )
A.f(x)=sinx B.f(x)=cosx
C.f(x)=sinx﹣cosx D.
(多选)10.(2025 河北模拟)已知直线l:x+ay﹣3=0与圆C:x2+y2﹣8x+6y+16=0,则下列说法正确的是( )
A.当a=2时,直线l与圆C相交
B.若直线l与圆C相切,则
C.圆C上一点P到直线l的最大距离为
D.若圆C上恰好有三个点到直线l的距离为2,则
(多选)11.(2025 遵义模拟)下列选项正确的是( )
A.若随机变量X~N(3,2),则E(X)=3
B.已知线性相关系数为r,若|r|越接近1,则两个变量的线性相关程度越高
C.回归直线方程为0.1x+1.4,则样本点(5,2)的残差为0.1
D.一组数x1,x2,…,xn(n∈N*)的平均数为a,若再插入一个数a,则这n+1个数的方差不变
三.填空题(共3小题)
12.(2025 浦东新区校级模拟)已知甲、乙两个盒子中各有10个球,其中甲盒内有1个黑球和9个白球,乙盒内有1个白球和9个黑球.现从两个盒子中随机挑选一盒,并从该盒中依次无放回地摸出两个球.则在第一次摸到黑球的条件下,第二次摸到白球的概率为 .
13.(2025 历下区校级模拟)已知等比数列{an}的前n项和为Sn,若5S2﹣4S4=0,a5﹣a7≠0,则 .
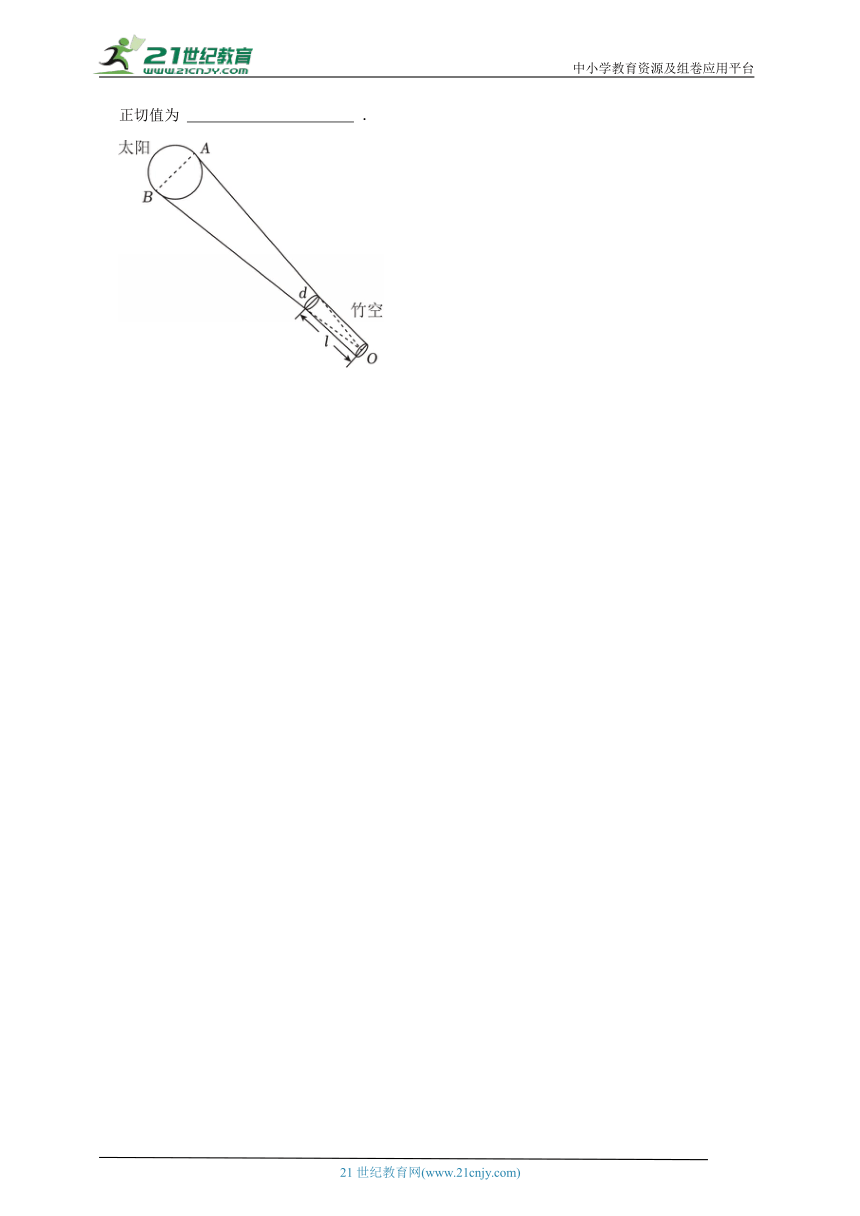
14.(2025 浦东新区校级模拟)《周髀算经》中“侧影探日行”一文有记载:“即取竹空,径一寸,长八尺,捕影而视之,空正掩目,而日应空之孔.”意为:“取竹空这一里筒,当里筒直径d是一寸,筒长l是八尺时(注;一尺等于十寸),从筒中搜捕太阳的边缘观察,则筒的内孔正好覆盖太阳,而太阳的外缘恰好填满竹管的内孔.”如图所示,O为竹空底面圆心,则太阳角∠AOB的正切值为 .
【江苏省考前冲刺特训】8+3+3模拟真题练习(三)-2025年高考数学
参考答案与试题解析
一.选择题(共8小题)
题号 1 2 3 4 5 6 7 8
答案 B C D C B A C A
二.多选题(共3小题)
题号 9 10 11
答案 CD AC ABC
一.选择题(共8小题)
1.(2025 九龙坡区校级一模)设集合A={x|x2﹣x﹣2≤0},B={x|y=lnx},则A∪B=( )
A.(0,2] B.[﹣1,+∞) C.(0,2) D.[﹣1,2]
【解答】解:由A={x|x2﹣x﹣2≤0}={x|﹣1≤x≤2},B={x|y=lnx}={x|x>0},
故A∪B=[﹣1,+∞).
故选:B.
2.(2025 山东校级一模)已知两个单位向量满足,则( )
A.0 B. C.1 D.2
【解答】解:已知两个单位向量满足,
则,
又,
则,
所以,
则,
所以.
故选:C.
3.(2025 四川模拟)赵爽是我国古代数学家,他为《周髀算经》一书作序时,介绍了“勾股圆方图”,亦称“赵爽弦图”(以弦为边长得到的正方形由4个全等的直角三角形再加上中间的一个小正方形组成).如图的“赵爽弦图”中小正方形的面积为49,大正方形的面积为169,直角三角形中较大的锐角为α,则sin2α=( )
A. B. C. D.
【解答】解:因为中小正方形的面积为49,大正方形的面积为169,
可得大、小正方形的边长分别为13,7,
于是有,
即有,两边平方可得sin2α+cos2α﹣2sinαcosα,
即,所以.
故选:D.
4.(2025 张家口三模)若(2﹣x)n的展开式中x2的系数为240,则n=( )
A.4 B.5 C.6 D.8
【解答】解:(2﹣x)n的展开式中x2的系数为(﹣1)22n﹣22n﹣2=240,
对于A,n=4时,,不满足方程;
对于B,n=5时,,不满足方程;
对于C,n=6时,,满足方程;
对于D,n=8时,,不满足方程.
故选:C.
5.(2025 临泉县校级三模)已知线段AB=5,AC=4,D为线段AB上一点,CD=2,记AB与AC的夹角为θ,若对于某个范围内任意固定的θ,总存在两个不同的△ACD符合题意,则cosθ的取值范围是( )
A. B. C. D.
【解答】解:由题意可知以C为圆心,2为半径的圆应与线段AB有两个公共点,
以A为坐标原点,AC为x轴,作图如下:
当AB与圆相切时,由r=2,AC=4,可得,
故.
当AB与圆相交,且点B刚好在圆上时,线段AB=5,AC=4,
D为线段AB上一点,CD=2,
记AB与AC的夹角为θ,如下图:
由余弦定理可得:,
所以cosθ的取值范围是.
故选:B.
6.(2025 沙坪坝区校级模拟)已知三棱柱ABC﹣A1B1C1的体积为1,E,F分别是棱BC,CA的中点,则以A,B,B1,A1,E,F为顶点的五面体的体积为( )
A. B. C. D.
【解答】解:设棱柱ABC﹣A1B1C1的底面积为S,高为h,
则三棱柱ABC﹣A1B1C1的体积为Sh=1,
又E,F分别是棱BC,CA的中点,
所以多边形EFC﹣A1B1C1为棱台,
所以该棱台的体积为,
所以所求几何体的体积为1.
故选:A.
7.(2025 龙华区校级模拟)已知F1,F2分别为双曲线C:的左、右焦点,A为双曲线C上的一点,且AF1⊥F1F2,|AF1|=3,,则双曲线C的离心率为( )
A. B. C. D.3
【解答】解:由题意,,可得,|AF1|=3,AF1⊥F1F2,
所以,
所以2a=6﹣3=3,所以.
故选:C.
8.(2025 湖北模拟)通信工程中常用n元数组(a1,a2,a3,…,an)表示信息,其中a1=0或1,且i,n∈N*.设u=(a1,a2,a3,…,an),v=(b1,b2,…,bn),d(u,v)表示u和v中相对应的元素不同的个数.如u=(1,0,0,1),v=(1,1,1,0),则d(u,v)=3.若u=(1,0,1,0,1,0),则使得d(u,v)=2的6元数组v的个数为( )
A.15 B.20 C.30 D.40
【解答】解:若u=(1,0,1,0,1,0),则满足d(u,v)=2,
字长为5的字v的个数为15.
故选:A.
二.多选题(共3小题)
(多选)9.(2025 罗湖区校级模拟)如果存在正实数a,使得f(x+a)为奇函数,f(x﹣a)为偶函数,我们称函数f(x)为”和谐函数”.则下列四个函数,是“和谐函数”的是( )
A.f(x)=sinx B.f(x)=cosx
C.f(x)=sinx﹣cosx D.
【解答】解:对于A,若f(x)=sinx是“和谐函数”,则a=kπ且,(k,m∈Z),a无解;
对于B,若f(x)=cosx是“和谐函数”,则a,a无解;
对于C,若是“和谐函数”,则且,a可取;
对于D,若是“和谐函数”,则,a可取.
故选:CD.
(多选)10.(2025 河北模拟)已知直线l:x+ay﹣3=0与圆C:x2+y2﹣8x+6y+16=0,则下列说法正确的是( )
A.当a=2时,直线l与圆C相交
B.若直线l与圆C相切,则
C.圆C上一点P到直线l的最大距离为
D.若圆C上恰好有三个点到直线l的距离为2,则
【解答】解:对于选项A:当a=2时,直线l:x+2y﹣3=0,圆C:x2+y2﹣8x+6y+16=0,圆C的标准方程为(x﹣4)2+(y+3)2=9,
可知圆的圆心C(4,﹣3),圆的半径r=3,则圆心C到直线l:x+2y﹣3=0的距离,
所以直线l与圆C相交,故A选项正确;
对于选项B:因为直线l与圆C相切,所以圆心C到直线l的距离,解得,故B选项错误;
对于选项C:因为直线l恒过定点(3,0),所以圆心C到直线l的最大距离,
则圆C上一点P到直线l的最大距离为,故C选项正确;
对于选项D:因为圆C上恰好有三个点到直线l的距离为2,
所以圆心C到直线l的距离,解得a=0或,故D选项错误.
故选:AC.
(多选)11.(2025 遵义模拟)下列选项正确的是( )
A.若随机变量X~N(3,2),则E(X)=3
B.已知线性相关系数为r,若|r|越接近1,则两个变量的线性相关程度越高
C.回归直线方程为0.1x+1.4,则样本点(5,2)的残差为0.1
D.一组数x1,x2,…,xn(n∈N*)的平均数为a,若再插入一个数a,则这n+1个数的方差不变
【解答】解:A选项:若X~N(3,2),则μ=3=E(X),A选项正确;
B选项:若线性相关系数的绝对值|r|越接近1,则两个变量的线性相关性越强,故B正确;
C选项:令x=5,得0.1×5+1.4=1.9,则所求残差为2﹣1.9=0.1,C选项正确;
D选项:由题意可知,若再插入一个数a,则平均数变为,
即平均数不变,而原来的数据的方差为,
同理可算得新数据的方差为,
所以方差可能改变,故D错误.
故选:ABC.
三.填空题(共3小题)
12.(2025 浦东新区校级模拟)已知甲、乙两个盒子中各有10个球,其中甲盒内有1个黑球和9个白球,乙盒内有1个白球和9个黑球.现从两个盒子中随机挑选一盒,并从该盒中依次无放回地摸出两个球.则在第一次摸到黑球的条件下,第二次摸到白球的概率为 .
【解答】解:根据题意,设事件A=“第一次摸到黑球”,B=“第二次摸到白球”,
则P(A),
P(AB),
故P(B|A).
故答案为:.
13.(2025 历下区校级模拟)已知等比数列{an}的前n项和为Sn,若5S2﹣4S4=0,a5﹣a7≠0,则 .
【解答】解:等比数列{an}的前n项和为Sn,若5S2﹣4S4=0,a5﹣a7≠0,
由5S2﹣4S4=0可得,
若a1+a2=0 q=﹣1,则与a5﹣a7≠0矛盾,
所以,
则.
故答案为:.
14.(2025 浦东新区校级模拟)《周髀算经》中“侧影探日行”一文有记载:“即取竹空,径一寸,长八尺,捕影而视之,空正掩目,而日应空之孔.”意为:“取竹空这一里筒,当里筒直径d是一寸,筒长l是八尺时(注;一尺等于十寸),从筒中搜捕太阳的边缘观察,则筒的内孔正好覆盖太阳,而太阳的外缘恰好填满竹管的内孔.”如图所示,O为竹空底面圆心,则太阳角∠AOB的正切值为 .
【解答】解:由题意可知,tan,
∴tan∠AOB.
故答案为:.
21世纪教育网 www.21cnjy.com 精品试卷·第 2 页 (共 2 页)
21世纪教育网(www.21cnjy.com)
【江苏省考前冲刺特训】8+3+3模拟真题练习(三)-2025年高考数学
一.选择题(共8小题)
1.(2025 九龙坡区校级一模)设集合A={x|x2﹣x﹣2≤0},B={x|y=lnx},则A∪B=( )
A.(0,2] B.[﹣1,+∞) C.(0,2) D.[﹣1,2]
2.(2025 山东校级一模)已知两个单位向量满足,则( )
A.0 B. C.1 D.2
3.(2025 四川模拟)赵爽是我国古代数学家,他为《周髀算经》一书作序时,介绍了“勾股圆方图”,亦称“赵爽弦图”(以弦为边长得到的正方形由4个全等的直角三角形再加上中间的一个小正方形组成).如图的“赵爽弦图”中小正方形的面积为49,大正方形的面积为169,直角三角形中较大的锐角为α,则sin2α=( )
A. B. C. D.
4.(2025 张家口三模)若(2﹣x)n的展开式中x2的系数为240,则n=( )
A.4 B.5 C.6 D.8
5.(2025 临泉县校级三模)已知线段AB=5,AC=4,D为线段AB上一点,CD=2,记AB与AC的夹角为θ,若对于某个范围内任意固定的θ,总存在两个不同的△ACD符合题意,则cosθ的取值范围是( )
A. B. C. D.
6.(2025 沙坪坝区校级模拟)已知三棱柱ABC﹣A1B1C1的体积为1,E,F分别是棱BC,CA的中点,则以A,B,B1,A1,E,F为顶点的五面体的体积为( )
A. B. C. D.
7.(2025 龙华区校级模拟)已知F1,F2分别为双曲线C:的左、右焦点,A为双曲线C上的一点,且AF1⊥F1F2,|AF1|=3,,则双曲线C的离心率为( )
A. B. C. D.3
8.(2025 湖北模拟)通信工程中常用n元数组(a1,a2,a3,…,an)表示信息,其中a1=0或1,且i,n∈N*.设u=(a1,a2,a3,…,an),v=(b1,b2,…,bn),d(u,v)表示u和v中相对应的元素不同的个数.如u=(1,0,0,1),v=(1,1,1,0),则d(u,v)=3.若u=(1,0,1,0,1,0),则使得d(u,v)=2的6元数组v的个数为( )
A.15 B.20 C.30 D.40
二.多选题(共3小题)
(多选)9.(2025 罗湖区校级模拟)如果存在正实数a,使得f(x+a)为奇函数,f(x﹣a)为偶函数,我们称函数f(x)为”和谐函数”.则下列四个函数,是“和谐函数”的是( )
A.f(x)=sinx B.f(x)=cosx
C.f(x)=sinx﹣cosx D.
(多选)10.(2025 河北模拟)已知直线l:x+ay﹣3=0与圆C:x2+y2﹣8x+6y+16=0,则下列说法正确的是( )
A.当a=2时,直线l与圆C相交
B.若直线l与圆C相切,则
C.圆C上一点P到直线l的最大距离为
D.若圆C上恰好有三个点到直线l的距离为2,则
(多选)11.(2025 遵义模拟)下列选项正确的是( )
A.若随机变量X~N(3,2),则E(X)=3
B.已知线性相关系数为r,若|r|越接近1,则两个变量的线性相关程度越高
C.回归直线方程为0.1x+1.4,则样本点(5,2)的残差为0.1
D.一组数x1,x2,…,xn(n∈N*)的平均数为a,若再插入一个数a,则这n+1个数的方差不变
三.填空题(共3小题)
12.(2025 浦东新区校级模拟)已知甲、乙两个盒子中各有10个球,其中甲盒内有1个黑球和9个白球,乙盒内有1个白球和9个黑球.现从两个盒子中随机挑选一盒,并从该盒中依次无放回地摸出两个球.则在第一次摸到黑球的条件下,第二次摸到白球的概率为 .
13.(2025 历下区校级模拟)已知等比数列{an}的前n项和为Sn,若5S2﹣4S4=0,a5﹣a7≠0,则 .
14.(2025 浦东新区校级模拟)《周髀算经》中“侧影探日行”一文有记载:“即取竹空,径一寸,长八尺,捕影而视之,空正掩目,而日应空之孔.”意为:“取竹空这一里筒,当里筒直径d是一寸,筒长l是八尺时(注;一尺等于十寸),从筒中搜捕太阳的边缘观察,则筒的内孔正好覆盖太阳,而太阳的外缘恰好填满竹管的内孔.”如图所示,O为竹空底面圆心,则太阳角∠AOB的正切值为 .
【江苏省考前冲刺特训】8+3+3模拟真题练习(三)-2025年高考数学
参考答案与试题解析
一.选择题(共8小题)
题号 1 2 3 4 5 6 7 8
答案 B C D C B A C A
二.多选题(共3小题)
题号 9 10 11
答案 CD AC ABC
一.选择题(共8小题)
1.(2025 九龙坡区校级一模)设集合A={x|x2﹣x﹣2≤0},B={x|y=lnx},则A∪B=( )
A.(0,2] B.[﹣1,+∞) C.(0,2) D.[﹣1,2]
【解答】解:由A={x|x2﹣x﹣2≤0}={x|﹣1≤x≤2},B={x|y=lnx}={x|x>0},
故A∪B=[﹣1,+∞).
故选:B.
2.(2025 山东校级一模)已知两个单位向量满足,则( )
A.0 B. C.1 D.2
【解答】解:已知两个单位向量满足,
则,
又,
则,
所以,
则,
所以.
故选:C.
3.(2025 四川模拟)赵爽是我国古代数学家,他为《周髀算经》一书作序时,介绍了“勾股圆方图”,亦称“赵爽弦图”(以弦为边长得到的正方形由4个全等的直角三角形再加上中间的一个小正方形组成).如图的“赵爽弦图”中小正方形的面积为49,大正方形的面积为169,直角三角形中较大的锐角为α,则sin2α=( )
A. B. C. D.
【解答】解:因为中小正方形的面积为49,大正方形的面积为169,
可得大、小正方形的边长分别为13,7,
于是有,
即有,两边平方可得sin2α+cos2α﹣2sinαcosα,
即,所以.
故选:D.
4.(2025 张家口三模)若(2﹣x)n的展开式中x2的系数为240,则n=( )
A.4 B.5 C.6 D.8
【解答】解:(2﹣x)n的展开式中x2的系数为(﹣1)22n﹣22n﹣2=240,
对于A,n=4时,,不满足方程;
对于B,n=5时,,不满足方程;
对于C,n=6时,,满足方程;
对于D,n=8时,,不满足方程.
故选:C.
5.(2025 临泉县校级三模)已知线段AB=5,AC=4,D为线段AB上一点,CD=2,记AB与AC的夹角为θ,若对于某个范围内任意固定的θ,总存在两个不同的△ACD符合题意,则cosθ的取值范围是( )
A. B. C. D.
【解答】解:由题意可知以C为圆心,2为半径的圆应与线段AB有两个公共点,
以A为坐标原点,AC为x轴,作图如下:
当AB与圆相切时,由r=2,AC=4,可得,
故.
当AB与圆相交,且点B刚好在圆上时,线段AB=5,AC=4,
D为线段AB上一点,CD=2,
记AB与AC的夹角为θ,如下图:
由余弦定理可得:,
所以cosθ的取值范围是.
故选:B.
6.(2025 沙坪坝区校级模拟)已知三棱柱ABC﹣A1B1C1的体积为1,E,F分别是棱BC,CA的中点,则以A,B,B1,A1,E,F为顶点的五面体的体积为( )
A. B. C. D.
【解答】解:设棱柱ABC﹣A1B1C1的底面积为S,高为h,
则三棱柱ABC﹣A1B1C1的体积为Sh=1,
又E,F分别是棱BC,CA的中点,
所以多边形EFC﹣A1B1C1为棱台,
所以该棱台的体积为,
所以所求几何体的体积为1.
故选:A.
7.(2025 龙华区校级模拟)已知F1,F2分别为双曲线C:的左、右焦点,A为双曲线C上的一点,且AF1⊥F1F2,|AF1|=3,,则双曲线C的离心率为( )
A. B. C. D.3
【解答】解:由题意,,可得,|AF1|=3,AF1⊥F1F2,
所以,
所以2a=6﹣3=3,所以.
故选:C.
8.(2025 湖北模拟)通信工程中常用n元数组(a1,a2,a3,…,an)表示信息,其中a1=0或1,且i,n∈N*.设u=(a1,a2,a3,…,an),v=(b1,b2,…,bn),d(u,v)表示u和v中相对应的元素不同的个数.如u=(1,0,0,1),v=(1,1,1,0),则d(u,v)=3.若u=(1,0,1,0,1,0),则使得d(u,v)=2的6元数组v的个数为( )
A.15 B.20 C.30 D.40
【解答】解:若u=(1,0,1,0,1,0),则满足d(u,v)=2,
字长为5的字v的个数为15.
故选:A.
二.多选题(共3小题)
(多选)9.(2025 罗湖区校级模拟)如果存在正实数a,使得f(x+a)为奇函数,f(x﹣a)为偶函数,我们称函数f(x)为”和谐函数”.则下列四个函数,是“和谐函数”的是( )
A.f(x)=sinx B.f(x)=cosx
C.f(x)=sinx﹣cosx D.
【解答】解:对于A,若f(x)=sinx是“和谐函数”,则a=kπ且,(k,m∈Z),a无解;
对于B,若f(x)=cosx是“和谐函数”,则a,a无解;
对于C,若是“和谐函数”,则且,a可取;
对于D,若是“和谐函数”,则,a可取.
故选:CD.
(多选)10.(2025 河北模拟)已知直线l:x+ay﹣3=0与圆C:x2+y2﹣8x+6y+16=0,则下列说法正确的是( )
A.当a=2时,直线l与圆C相交
B.若直线l与圆C相切,则
C.圆C上一点P到直线l的最大距离为
D.若圆C上恰好有三个点到直线l的距离为2,则
【解答】解:对于选项A:当a=2时,直线l:x+2y﹣3=0,圆C:x2+y2﹣8x+6y+16=0,圆C的标准方程为(x﹣4)2+(y+3)2=9,
可知圆的圆心C(4,﹣3),圆的半径r=3,则圆心C到直线l:x+2y﹣3=0的距离,
所以直线l与圆C相交,故A选项正确;
对于选项B:因为直线l与圆C相切,所以圆心C到直线l的距离,解得,故B选项错误;
对于选项C:因为直线l恒过定点(3,0),所以圆心C到直线l的最大距离,
则圆C上一点P到直线l的最大距离为,故C选项正确;
对于选项D:因为圆C上恰好有三个点到直线l的距离为2,
所以圆心C到直线l的距离,解得a=0或,故D选项错误.
故选:AC.
(多选)11.(2025 遵义模拟)下列选项正确的是( )
A.若随机变量X~N(3,2),则E(X)=3
B.已知线性相关系数为r,若|r|越接近1,则两个变量的线性相关程度越高
C.回归直线方程为0.1x+1.4,则样本点(5,2)的残差为0.1
D.一组数x1,x2,…,xn(n∈N*)的平均数为a,若再插入一个数a,则这n+1个数的方差不变
【解答】解:A选项:若X~N(3,2),则μ=3=E(X),A选项正确;
B选项:若线性相关系数的绝对值|r|越接近1,则两个变量的线性相关性越强,故B正确;
C选项:令x=5,得0.1×5+1.4=1.9,则所求残差为2﹣1.9=0.1,C选项正确;
D选项:由题意可知,若再插入一个数a,则平均数变为,
即平均数不变,而原来的数据的方差为,
同理可算得新数据的方差为,
所以方差可能改变,故D错误.
故选:ABC.
三.填空题(共3小题)
12.(2025 浦东新区校级模拟)已知甲、乙两个盒子中各有10个球,其中甲盒内有1个黑球和9个白球,乙盒内有1个白球和9个黑球.现从两个盒子中随机挑选一盒,并从该盒中依次无放回地摸出两个球.则在第一次摸到黑球的条件下,第二次摸到白球的概率为 .
【解答】解:根据题意,设事件A=“第一次摸到黑球”,B=“第二次摸到白球”,
则P(A),
P(AB),
故P(B|A).
故答案为:.
13.(2025 历下区校级模拟)已知等比数列{an}的前n项和为Sn,若5S2﹣4S4=0,a5﹣a7≠0,则 .
【解答】解:等比数列{an}的前n项和为Sn,若5S2﹣4S4=0,a5﹣a7≠0,
由5S2﹣4S4=0可得,
若a1+a2=0 q=﹣1,则与a5﹣a7≠0矛盾,
所以,
则.
故答案为:.
14.(2025 浦东新区校级模拟)《周髀算经》中“侧影探日行”一文有记载:“即取竹空,径一寸,长八尺,捕影而视之,空正掩目,而日应空之孔.”意为:“取竹空这一里筒,当里筒直径d是一寸,筒长l是八尺时(注;一尺等于十寸),从筒中搜捕太阳的边缘观察,则筒的内孔正好覆盖太阳,而太阳的外缘恰好填满竹管的内孔.”如图所示,O为竹空底面圆心,则太阳角∠AOB的正切值为 .
【解答】解:由题意可知,tan,
∴tan∠AOB.
故答案为:.
21世纪教育网 www.21cnjy.com 精品试卷·第 2 页 (共 2 页)
21世纪教育网(www.21cnjy.com)
同课章节目录
