期末必考应用专题:长方体(一)和长方体(二)(真题演练)(含答案)-2024-2025学年数学五年级下册北师大版
文档属性
| 名称 | 期末必考应用专题:长方体(一)和长方体(二)(真题演练)(含答案)-2024-2025学年数学五年级下册北师大版 |  | |
| 格式 | docx | ||
| 文件大小 | 738.0KB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 北师大版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2025-05-29 12:19:15 | ||
图片预览


文档简介
中小学教育资源及组卷应用平台
期末必考应用专题:长方体(一)和长方体(二)(真题演练)-2024-2025学年数学五年级下册北师大版
1.(2025春 龙岗区期末)小敏的好朋友要过生日了,小敏准备用彩色丝带把礼品盒包装一下(如图),要捆扎这个礼品盒,如果接头处共长10分米,需要多少米的丝带?
2.(2025春 榕城区期末)一个长30cm,宽25cm,高8cm的饼干盒,要在它的四周贴上一圈商标纸,至少需要多大面积的商标纸?
3.(2025春 东西湖区期末)包装礼盒时,需要在外面系上彩带(如图),打结部分长24厘米。按照图中方式,包装这个礼盒需要多长的彩带?(单位:厘米)
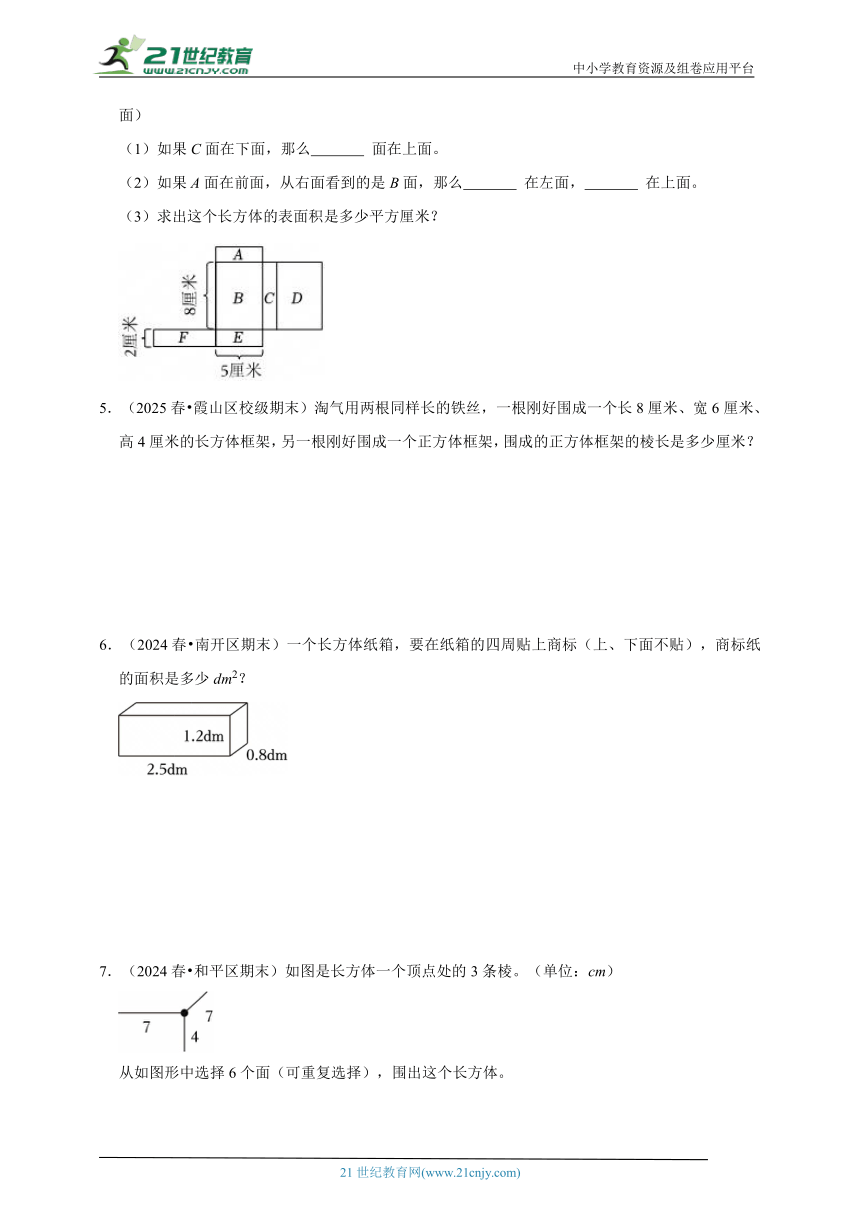
4.(2025春 忠县期末)如图是一个长方体的展开图,如果将它还原成长方体。(所有字母露在外面)
(1)如果C面在下面,那么 面在上面。
(2)如果A面在前面,从右面看到的是B面,那么 在左面, 在上面。
(3)求出这个长方体的表面积是多少平方厘米?
5.(2025春 霞山区校级期末)淘气用两根同样长的铁丝,一根刚好围成一个长8厘米、宽6厘米、高4厘米的长方体框架,另一根刚好围成一个正方体框架,围成的正方体框架的棱长是多少厘米?
6.(2024春 南开区期末)一个长方体纸箱,要在纸箱的四周贴上商标(上、下面不贴),商标纸的面积是多少dm2?
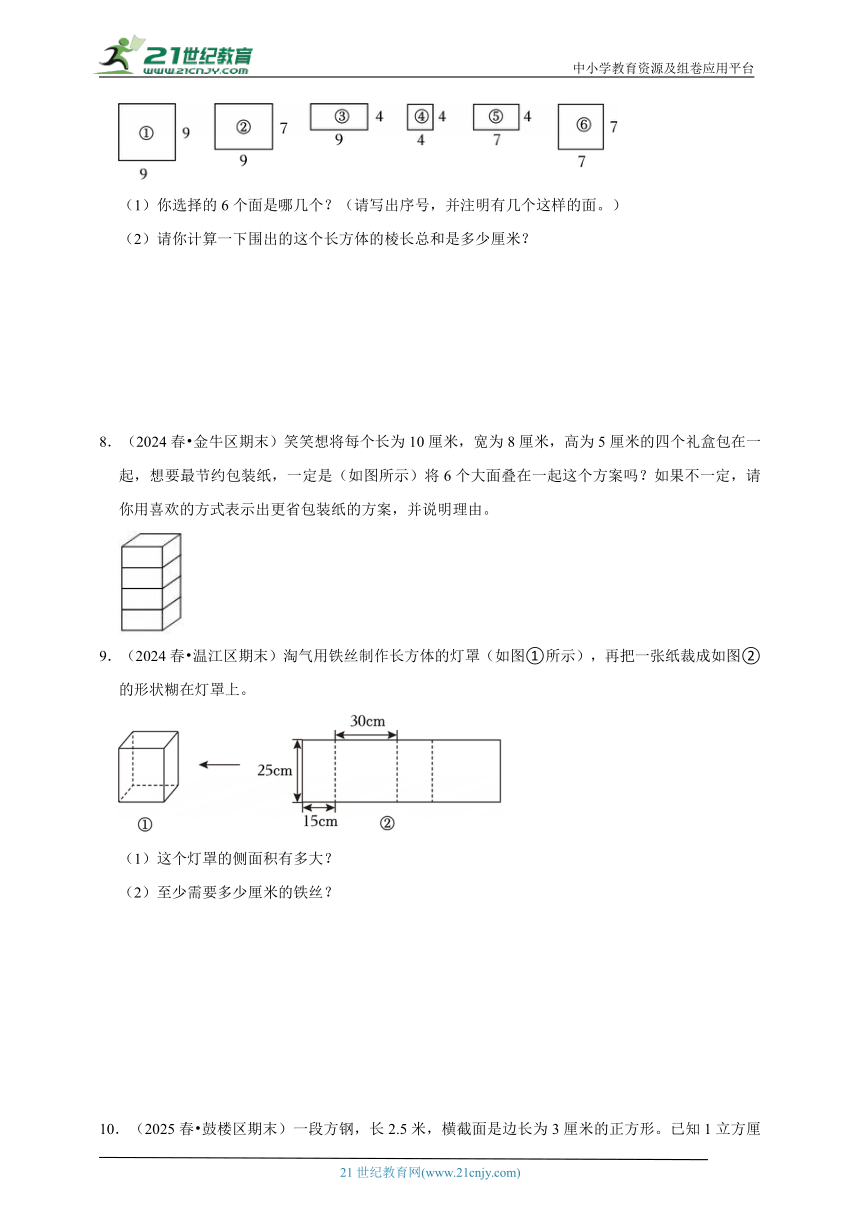
7.(2024春 和平区期末)如图是长方体一个顶点处的3条棱。(单位:cm)
从如图形中选择6个面(可重复选择),围出这个长方体。
(1)你选择的6个面是哪几个?(请写出序号,并注明有几个这样的面。)
(2)请你计算一下围出的这个长方体的棱长总和是多少厘米?
8.(2024春 金牛区期末)笑笑想将每个长为10厘米,宽为8厘米,高为5厘米的四个礼盒包在一起,想要最节约包装纸,一定是(如图所示)将6个大面叠在一起这个方案吗?如果不一定,请你用喜欢的方式表示出更省包装纸的方案,并说明理由。
9.(2024春 温江区期末)淘气用铁丝制作长方体的灯罩(如图①所示),再把一张纸裁成如图②的形状糊在灯罩上。
(1)这个灯罩的侧面积有多大?
(2)至少需要多少厘米的铁丝?
10.(2025春 鼓楼区期末)一段方钢,长2.5米,横截面是边长为3厘米的正方形。已知1立方厘米的方钢重7.8克,这段方钢重多少千克?
11.(2025春 鼓楼区期末)有一个无水的观赏鱼缸(如图),里面放有一块高为38厘米的假山石。如果水龙头以每分钟12升的流量向鱼缸内注水,3.45分钟后恰好将假山石完全淹没,那么假山石的体积是多少?
12.(2025春 甘井子区期末)李老师用铁丝制作了一个长25cm,宽15cm,高2dm的长方体框架。如果用这根铁丝围成一个正方体,正方体的体积是多少立方分米?
13.(2025春 怀宁县期末)浩浩用一根铁丝做了一个棱长是6厘米的正方体框架,如果用这根铁丝做成长8厘米、宽5厘米的长方体框架,那么这个长方体的高是多少?体积是多少?
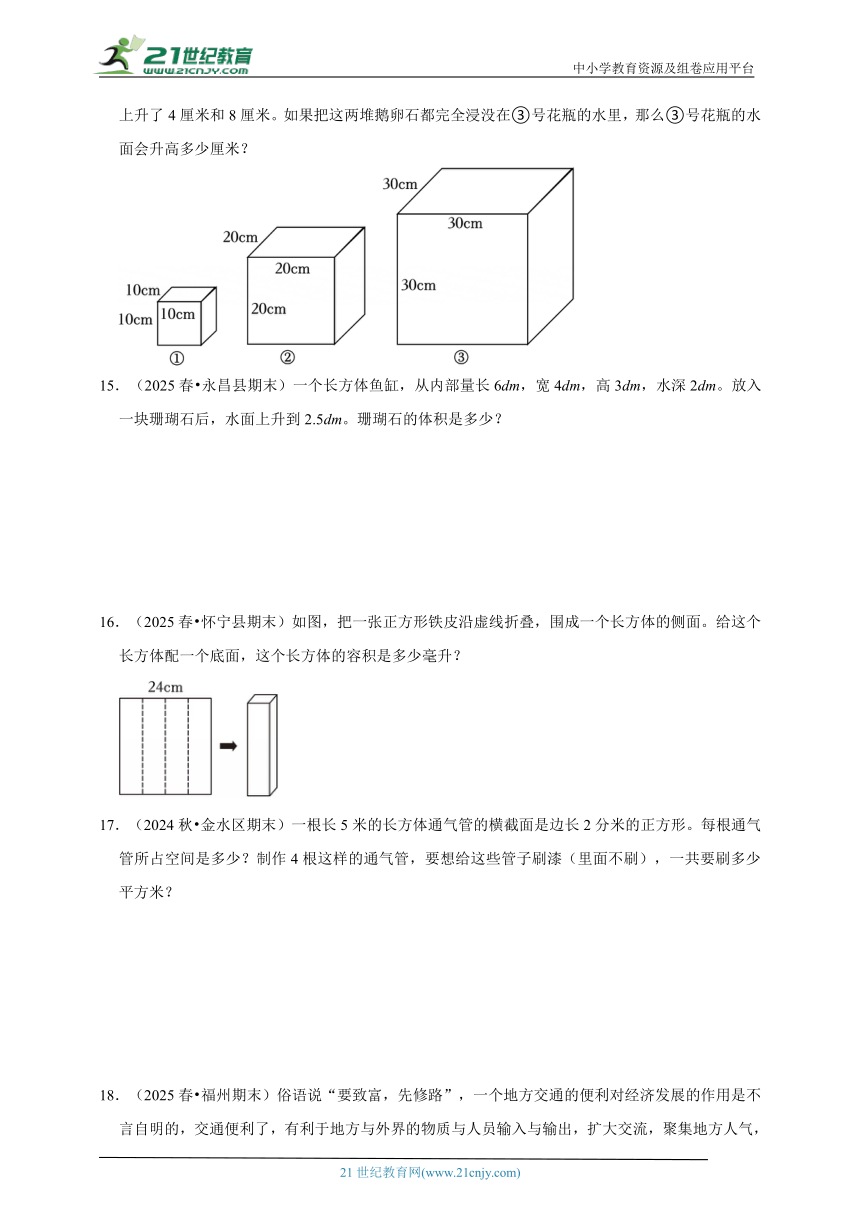
14.(2024秋 包河区期末)如图,科学实验小组的同学们准备了大小不同的三个正方体水培花瓶。他们把两堆鹅卵石分别完全浸没在①号、②号两个正方体水培花瓶的水里,两个花瓶的水面分别上升了4厘米和8厘米。如果把这两堆鹅卵石都完全浸没在③号花瓶的水里,那么③号花瓶的水面会升高多少厘米?
15.(2025春 永昌县期末)一个长方体鱼缸,从内部量长6dm,宽4dm,高3dm,水深2dm。放入一块珊瑚石后,水面上升到2.5dm。珊瑚石的体积是多少?
16.(2025春 怀宁县期末)如图,把一张正方形铁皮沿虚线折叠,围成一个长方体的侧面。给这个长方体配一个底面,这个长方体的容积是多少毫升?
17.(2024秋 金水区期末)一根长5米的长方体通气管的横截面是边长2分米的正方形。每根通气管所占空间是多少?制作4根这样的通气管,要想给这些管子刷漆(里面不刷),一共要刷多少平方米?
18.(2025春 福州期末)俗语说“要致富,先修路”,一个地方交通的便利对经济发展的作用是不言自明的,交通便利了,有利于地方与外界的物质与人员输入与输出,扩大交流,聚集地方人气,增加城市名气,人口增长,进而加快地方城市化进程,各个产业部门才有进一步发展的可能,扩大城市辐射范围。A市为了促进城市发展,需要修筑一些路面,某工程队接到一项修路任务后,准备用120立方米的沙子铺成一条宽5米的小路,沙子铺1分米厚,这条小路可以铺多长?
19.(2025春 瑞安市期末)一个长方体玻璃缸,从里面量长4dm,宽3dm,高4dm,里面装有2dm深的水,如果在玻璃缸内放入一个棱长3dm的正方体铁块,完全浸没后,那么水将会溢出多少升?
20.(2025春 碑林区期末)用如图所示的五块长方形的亚克力板可以制作一个无盖的长方体。将这个长方体装满水,再倒一部分到一个棱长为2dm的正方体容器中,使得两个容器中的水面同样高,这时两个容器中的水面高度是多少分米?(容器壁厚度忽略不计)
21.(2025 北碚区)一个高1米的直柱体容器如图1所示,俯视图如图2所示(单位:分米)。容器中有甲、乙两块挡板(挡板的体积忽略不计)将容器分成A、B、C三个区域,其中甲挡板高6分米,乙挡板高8分米。往C区域匀速注水,10分钟后,B区域水的高度是3分米。
(1)每分钟注水多少升?
(2)如果往C区域注水的同时以同样的速度往A区域注水,多少分钟后,A区域水的高度是B区域的2倍?
期末必考应用专题:长方体(一)和长方体(二)(真题演练)-2024-2025学年数学五年级下册北师大版
参考答案与试题解析
一.应用题(共21小题)
1.(2025春 龙岗区期末)小敏的好朋友要过生日了,小敏准备用彩色丝带把礼品盒包装一下(如图),要捆扎这个礼品盒,如果接头处共长10分米,需要多少米的丝带?
【解答】解:3×2+2×2+1×4+10
=6+4+4+10
=24(分米)
24分米=2.4米
答:需要2.4米的丝带。
2.(2025春 榕城区期末)一个长30cm,宽25cm,高8cm的饼干盒,要在它的四周贴上一圈商标纸,至少需要多大面积的商标纸?
【解答】解:前后两个面的面积为2×(30×8)=480(平方厘米)
左右两个面的面积为2×(25×8)=400(平方厘米)
商标纸面积为480+400=880(平方厘米)
答:至少需要880平方厘米的商标纸。
3.(2025春 东西湖区期末)包装礼盒时,需要在外面系上彩带(如图),打结部分长24厘米。按照图中方式,包装这个礼盒需要多长的彩带?(单位:厘米)
【解答】解:22.5×2+20×4+8×2+24
=45+80+16+24
=125+16+24
=141+24
=165(厘米)
答:包装这个礼盒需要165厘米的彩带。
4.(2025春 忠县期末)如图是一个长方体的展开图,如果将它还原成长方体。(所有字母露在外面)
(1)如果C面在下面,那么 F 面在上面。
(2)如果A面在前面,从右面看到的是B面,那么 D 在左面, C 在上面。
(3)求出这个长方体的表面积是多少平方厘米?
【解答】解:(1)F面在上面。
(2)D在左面,C在上面。
(3)(8×5+8×2+5×2)×2
=(40+16+10)×2
=66×2
=132(平方厘米)
答:这个长方体的表面积是132平方厘米。
故答案为:F;D;C。
5.(2025春 霞山区校级期末)淘气用两根同样长的铁丝,一根刚好围成一个长8厘米、宽6厘米、高4厘米的长方体框架,另一根刚好围成一个正方体框架,围成的正方体框架的棱长是多少厘米?
【解答】解:(8+6+4)×4
=18×4
=72(厘米)
72÷12=6(厘米)
答:围成的正方体框架的棱长是6厘米。
6.(2024春 南开区期末)一个长方体纸箱,要在纸箱的四周贴上商标(上、下面不贴),商标纸的面积是多少dm2?
【解答】解:(2.5+0.8)×2×1.2
=3.3×2×1.2
=6.6×1.2
=7.92(平方分米)
答:商标纸的面积是7.92平方分米。
7.(2024春 和平区期末)如图是长方体一个顶点处的3条棱。(单位:cm)
从如图形中选择6个面(可重复选择),围出这个长方体。
(1)你选择的6个面是哪几个?(请写出序号,并注明有几个这样的面。)
(2)请你计算一下围出的这个长方体的棱长总和是多少厘米?
【解答】解:(1)有4个⑤,2个⑥;
(2)(7+7+4)×4
=18×4
=72(厘米)
答:这个长方体的棱长总和是72厘米。
8.(2024春 金牛区期末)笑笑想将每个长为10厘米,宽为8厘米,高为5厘米的四个礼盒包在一起,想要最节约包装纸,一定是(如图所示)将6个大面叠在一起这个方案吗?如果不一定,请你用喜欢的方式表示出更省包装纸的方案,并说明理由。
【解答】解:第一种:
5×4=20(厘米)
(8×10+8×20+10×20)×2
=(80+160+200)×2
=440×2
=880(平方厘米)
第二种:
8×2=16(厘米)
5×2=10(厘米)
(16×10+16×10+10×10)×2
=(160+160+100)×2
=420×2
=840(平方厘米)
840<880
所以将6个大面叠在一起这个方案不是最省包装纸的方案,第二种方案更省包装纸。
9.(2024春 温江区期末)淘气用铁丝制作长方体的灯罩(如图①所示),再把一张纸裁成如图②的形状糊在灯罩上。
(1)这个灯罩的侧面积有多大?
(2)至少需要多少厘米的铁丝?
【解答】解:(1)这个灯罩的侧面积:
(30×25+15×25)×2
=(750+375)×2
=1125×2
=2250(平方厘米)
答:这个灯罩的侧面积是2250平方厘米。
(2)至少需要铁丝的长度:
(30+15+25)×4
=(45+25)×4
=70×4
=280(厘米)
答:至少需要280厘米的铁丝。
10.(2025春 鼓楼区期末)一段方钢,长2.5米,横截面是边长为3厘米的正方形。已知1立方厘米的方钢重7.8克,这段方钢重多少千克?
【解答】解:先把方钢的长度换算成用厘米作单位。
2.5米=250厘米
3×3×250×7.8
=9×250×7.8
=2250×7.8
=17550(克)
17550克=17.55千克
答:这段方钢重17.55千克。
11.(2025春 鼓楼区期末)有一个无水的观赏鱼缸(如图),里面放有一块高为38厘米的假山石。如果水龙头以每分钟12升的流量向鱼缸内注水,3.45分钟后恰好将假山石完全淹没,那么假山石的体积是多少?
【解答】解:12升=12000毫升
12000毫升=12000立方厘米
48×25×38﹣12000×3.45
=1200×38﹣41400
=45600﹣41400
=4200(立方厘米)
答:假山石的体积是4200立方厘米。
12.(2025春 甘井子区期末)李老师用铁丝制作了一个长25cm,宽15cm,高2dm的长方体框架。如果用这根铁丝围成一个正方体,正方体的体积是多少立方分米?
【解答】解:(2.5+1.5+2)×4÷12
=6×4÷12
=2(分米)
2×2×2
=4×2
=8(立方分米)
答:正方体的体积是8立方分米。
13.(2025春 怀宁县期末)浩浩用一根铁丝做了一个棱长是6厘米的正方体框架,如果用这根铁丝做成长8厘米、宽5厘米的长方体框架,那么这个长方体的高是多少?体积是多少?
【解答】解:6×12÷4﹣(8+5)
=72÷4﹣13
=18﹣13
=5(厘米)
8×5×5=200(立方厘米)
答:这个长方体的高是5厘米,体积是200立方厘米。
14.(2024秋 包河区期末)如图,科学实验小组的同学们准备了大小不同的三个正方体水培花瓶。他们把两堆鹅卵石分别完全浸没在①号、②号两个正方体水培花瓶的水里,两个花瓶的水面分别上升了4厘米和8厘米。如果把这两堆鹅卵石都完全浸没在③号花瓶的水里,那么③号花瓶的水面会升高多少厘米?
【解答】解:(10×10×4+20×20×8)÷(30×30)
=3600÷900
=4(厘米)
答:把这两堆鹅卵石都完全浸没在③号花瓶的水里,那么③号花瓶的水面会升高4厘米。
15.(2025春 永昌县期末)一个长方体鱼缸,从内部量长6dm,宽4dm,高3dm,水深2dm。放入一块珊瑚石后,水面上升到2.5dm。珊瑚石的体积是多少?
【解答】解:6×4×(2.5﹣2)
=24×0.5
=12(立方分米)
答:珊瑚石的体积是12立方分米。
16.(2025春 怀宁县期末)如图,把一张正方形铁皮沿虚线折叠,围成一个长方体的侧面。给这个长方体配一个底面,这个长方体的容积是多少毫升?
【解答】解:24÷4=6(厘米)
6×6×24
=36×24
=864(立方厘米)
864立方厘米=864毫升
答:这个长方体的容积是864毫升。
17.(2024秋 金水区期末)一根长5米的长方体通气管的横截面是边长2分米的正方形。每根通气管所占空间是多少?制作4根这样的通气管,要想给这些管子刷漆(里面不刷),一共要刷多少平方米?
【解答】解:5米=50分米
2×2×50=200(立方分米)
2×50×4×4
=100×16
=1600(平方分米)
1600平方分米=16平方米
答:每根通气管所占空间200立方分米,一共要刷16平方米。
18.(2025春 福州期末)俗语说“要致富,先修路”,一个地方交通的便利对经济发展的作用是不言自明的,交通便利了,有利于地方与外界的物质与人员输入与输出,扩大交流,聚集地方人气,增加城市名气,人口增长,进而加快地方城市化进程,各个产业部门才有进一步发展的可能,扩大城市辐射范围。A市为了促进城市发展,需要修筑一些路面,某工程队接到一项修路任务后,准备用120立方米的沙子铺成一条宽5米的小路,沙子铺1分米厚,这条小路可以铺多长?
【解答】解:1分米=0.1米
120÷5÷0.1
=24÷0.1
=240(米)
答:这条小路可以铺240米长。
19.(2025春 瑞安市期末)一个长方体玻璃缸,从里面量长4dm,宽3dm,高4dm,里面装有2dm深的水,如果在玻璃缸内放入一个棱长3dm的正方体铁块,完全浸没后,那么水将会溢出多少升?
【解答】解:4﹣2=2(dm)
4×3×2=24(立方分米)
3×3×3=27(立方分米)
27﹣24=3(立方分米)
3立方分米=3L
答:水将会溢出3升。
20.(2025春 碑林区期末)用如图所示的五块长方形的亚克力板可以制作一个无盖的长方体。将这个长方体装满水,再倒一部分到一个棱长为2dm的正方体容器中,使得两个容器中的水面同样高,这时两个容器中的水面高度是多少分米?(容器壁厚度忽略不计)
【解答】解:3×2×1÷(3×2+2×2)
=6÷10
=0.6(分米)
答:这时两个容器中的水面高度是0.6分米。
21.(2025 北碚区)一个高1米的直柱体容器如图1所示,俯视图如图2所示(单位:分米)。容器中有甲、乙两块挡板(挡板的体积忽略不计)将容器分成A、B、C三个区域,其中甲挡板高6分米,乙挡板高8分米。往C区域匀速注水,10分钟后,B区域水的高度是3分米。
(1)每分钟注水多少升?
(2)如果往C区域注水的同时以同样的速度往A区域注水,多少分钟后,A区域水的高度是B区域的2倍?
【解答】解:(1)2×4×6+2×2×3
=8×6+4×3
=48+12
=60(立方分米)
60立方分米=60升
60÷10=6(升)
答:每分钟注水6升。
(2)2×4×6÷6
=8×6÷6
=8(分钟)
6×8÷(2×6)
=48÷12
=4(分米)
设还需t分钟,A区域水位是B区域的2倍,
t=1.6
8+1.6=9.6(分钟)
答:9.6分钟后,A区域水位是B区域的2倍。
21世纪教育网 www.21cnjy.com 精品试卷·第 2 页 (共 2 页)
21世纪教育网(www.21cnjy.com)
期末必考应用专题:长方体(一)和长方体(二)(真题演练)-2024-2025学年数学五年级下册北师大版
1.(2025春 龙岗区期末)小敏的好朋友要过生日了,小敏准备用彩色丝带把礼品盒包装一下(如图),要捆扎这个礼品盒,如果接头处共长10分米,需要多少米的丝带?
2.(2025春 榕城区期末)一个长30cm,宽25cm,高8cm的饼干盒,要在它的四周贴上一圈商标纸,至少需要多大面积的商标纸?
3.(2025春 东西湖区期末)包装礼盒时,需要在外面系上彩带(如图),打结部分长24厘米。按照图中方式,包装这个礼盒需要多长的彩带?(单位:厘米)
4.(2025春 忠县期末)如图是一个长方体的展开图,如果将它还原成长方体。(所有字母露在外面)
(1)如果C面在下面,那么 面在上面。
(2)如果A面在前面,从右面看到的是B面,那么 在左面, 在上面。
(3)求出这个长方体的表面积是多少平方厘米?
5.(2025春 霞山区校级期末)淘气用两根同样长的铁丝,一根刚好围成一个长8厘米、宽6厘米、高4厘米的长方体框架,另一根刚好围成一个正方体框架,围成的正方体框架的棱长是多少厘米?
6.(2024春 南开区期末)一个长方体纸箱,要在纸箱的四周贴上商标(上、下面不贴),商标纸的面积是多少dm2?
7.(2024春 和平区期末)如图是长方体一个顶点处的3条棱。(单位:cm)
从如图形中选择6个面(可重复选择),围出这个长方体。
(1)你选择的6个面是哪几个?(请写出序号,并注明有几个这样的面。)
(2)请你计算一下围出的这个长方体的棱长总和是多少厘米?
8.(2024春 金牛区期末)笑笑想将每个长为10厘米,宽为8厘米,高为5厘米的四个礼盒包在一起,想要最节约包装纸,一定是(如图所示)将6个大面叠在一起这个方案吗?如果不一定,请你用喜欢的方式表示出更省包装纸的方案,并说明理由。
9.(2024春 温江区期末)淘气用铁丝制作长方体的灯罩(如图①所示),再把一张纸裁成如图②的形状糊在灯罩上。
(1)这个灯罩的侧面积有多大?
(2)至少需要多少厘米的铁丝?
10.(2025春 鼓楼区期末)一段方钢,长2.5米,横截面是边长为3厘米的正方形。已知1立方厘米的方钢重7.8克,这段方钢重多少千克?
11.(2025春 鼓楼区期末)有一个无水的观赏鱼缸(如图),里面放有一块高为38厘米的假山石。如果水龙头以每分钟12升的流量向鱼缸内注水,3.45分钟后恰好将假山石完全淹没,那么假山石的体积是多少?
12.(2025春 甘井子区期末)李老师用铁丝制作了一个长25cm,宽15cm,高2dm的长方体框架。如果用这根铁丝围成一个正方体,正方体的体积是多少立方分米?
13.(2025春 怀宁县期末)浩浩用一根铁丝做了一个棱长是6厘米的正方体框架,如果用这根铁丝做成长8厘米、宽5厘米的长方体框架,那么这个长方体的高是多少?体积是多少?
14.(2024秋 包河区期末)如图,科学实验小组的同学们准备了大小不同的三个正方体水培花瓶。他们把两堆鹅卵石分别完全浸没在①号、②号两个正方体水培花瓶的水里,两个花瓶的水面分别上升了4厘米和8厘米。如果把这两堆鹅卵石都完全浸没在③号花瓶的水里,那么③号花瓶的水面会升高多少厘米?
15.(2025春 永昌县期末)一个长方体鱼缸,从内部量长6dm,宽4dm,高3dm,水深2dm。放入一块珊瑚石后,水面上升到2.5dm。珊瑚石的体积是多少?
16.(2025春 怀宁县期末)如图,把一张正方形铁皮沿虚线折叠,围成一个长方体的侧面。给这个长方体配一个底面,这个长方体的容积是多少毫升?
17.(2024秋 金水区期末)一根长5米的长方体通气管的横截面是边长2分米的正方形。每根通气管所占空间是多少?制作4根这样的通气管,要想给这些管子刷漆(里面不刷),一共要刷多少平方米?
18.(2025春 福州期末)俗语说“要致富,先修路”,一个地方交通的便利对经济发展的作用是不言自明的,交通便利了,有利于地方与外界的物质与人员输入与输出,扩大交流,聚集地方人气,增加城市名气,人口增长,进而加快地方城市化进程,各个产业部门才有进一步发展的可能,扩大城市辐射范围。A市为了促进城市发展,需要修筑一些路面,某工程队接到一项修路任务后,准备用120立方米的沙子铺成一条宽5米的小路,沙子铺1分米厚,这条小路可以铺多长?
19.(2025春 瑞安市期末)一个长方体玻璃缸,从里面量长4dm,宽3dm,高4dm,里面装有2dm深的水,如果在玻璃缸内放入一个棱长3dm的正方体铁块,完全浸没后,那么水将会溢出多少升?
20.(2025春 碑林区期末)用如图所示的五块长方形的亚克力板可以制作一个无盖的长方体。将这个长方体装满水,再倒一部分到一个棱长为2dm的正方体容器中,使得两个容器中的水面同样高,这时两个容器中的水面高度是多少分米?(容器壁厚度忽略不计)
21.(2025 北碚区)一个高1米的直柱体容器如图1所示,俯视图如图2所示(单位:分米)。容器中有甲、乙两块挡板(挡板的体积忽略不计)将容器分成A、B、C三个区域,其中甲挡板高6分米,乙挡板高8分米。往C区域匀速注水,10分钟后,B区域水的高度是3分米。
(1)每分钟注水多少升?
(2)如果往C区域注水的同时以同样的速度往A区域注水,多少分钟后,A区域水的高度是B区域的2倍?
期末必考应用专题:长方体(一)和长方体(二)(真题演练)-2024-2025学年数学五年级下册北师大版
参考答案与试题解析
一.应用题(共21小题)
1.(2025春 龙岗区期末)小敏的好朋友要过生日了,小敏准备用彩色丝带把礼品盒包装一下(如图),要捆扎这个礼品盒,如果接头处共长10分米,需要多少米的丝带?
【解答】解:3×2+2×2+1×4+10
=6+4+4+10
=24(分米)
24分米=2.4米
答:需要2.4米的丝带。
2.(2025春 榕城区期末)一个长30cm,宽25cm,高8cm的饼干盒,要在它的四周贴上一圈商标纸,至少需要多大面积的商标纸?
【解答】解:前后两个面的面积为2×(30×8)=480(平方厘米)
左右两个面的面积为2×(25×8)=400(平方厘米)
商标纸面积为480+400=880(平方厘米)
答:至少需要880平方厘米的商标纸。
3.(2025春 东西湖区期末)包装礼盒时,需要在外面系上彩带(如图),打结部分长24厘米。按照图中方式,包装这个礼盒需要多长的彩带?(单位:厘米)
【解答】解:22.5×2+20×4+8×2+24
=45+80+16+24
=125+16+24
=141+24
=165(厘米)
答:包装这个礼盒需要165厘米的彩带。
4.(2025春 忠县期末)如图是一个长方体的展开图,如果将它还原成长方体。(所有字母露在外面)
(1)如果C面在下面,那么 F 面在上面。
(2)如果A面在前面,从右面看到的是B面,那么 D 在左面, C 在上面。
(3)求出这个长方体的表面积是多少平方厘米?
【解答】解:(1)F面在上面。
(2)D在左面,C在上面。
(3)(8×5+8×2+5×2)×2
=(40+16+10)×2
=66×2
=132(平方厘米)
答:这个长方体的表面积是132平方厘米。
故答案为:F;D;C。
5.(2025春 霞山区校级期末)淘气用两根同样长的铁丝,一根刚好围成一个长8厘米、宽6厘米、高4厘米的长方体框架,另一根刚好围成一个正方体框架,围成的正方体框架的棱长是多少厘米?
【解答】解:(8+6+4)×4
=18×4
=72(厘米)
72÷12=6(厘米)
答:围成的正方体框架的棱长是6厘米。
6.(2024春 南开区期末)一个长方体纸箱,要在纸箱的四周贴上商标(上、下面不贴),商标纸的面积是多少dm2?
【解答】解:(2.5+0.8)×2×1.2
=3.3×2×1.2
=6.6×1.2
=7.92(平方分米)
答:商标纸的面积是7.92平方分米。
7.(2024春 和平区期末)如图是长方体一个顶点处的3条棱。(单位:cm)
从如图形中选择6个面(可重复选择),围出这个长方体。
(1)你选择的6个面是哪几个?(请写出序号,并注明有几个这样的面。)
(2)请你计算一下围出的这个长方体的棱长总和是多少厘米?
【解答】解:(1)有4个⑤,2个⑥;
(2)(7+7+4)×4
=18×4
=72(厘米)
答:这个长方体的棱长总和是72厘米。
8.(2024春 金牛区期末)笑笑想将每个长为10厘米,宽为8厘米,高为5厘米的四个礼盒包在一起,想要最节约包装纸,一定是(如图所示)将6个大面叠在一起这个方案吗?如果不一定,请你用喜欢的方式表示出更省包装纸的方案,并说明理由。
【解答】解:第一种:
5×4=20(厘米)
(8×10+8×20+10×20)×2
=(80+160+200)×2
=440×2
=880(平方厘米)
第二种:
8×2=16(厘米)
5×2=10(厘米)
(16×10+16×10+10×10)×2
=(160+160+100)×2
=420×2
=840(平方厘米)
840<880
所以将6个大面叠在一起这个方案不是最省包装纸的方案,第二种方案更省包装纸。
9.(2024春 温江区期末)淘气用铁丝制作长方体的灯罩(如图①所示),再把一张纸裁成如图②的形状糊在灯罩上。
(1)这个灯罩的侧面积有多大?
(2)至少需要多少厘米的铁丝?
【解答】解:(1)这个灯罩的侧面积:
(30×25+15×25)×2
=(750+375)×2
=1125×2
=2250(平方厘米)
答:这个灯罩的侧面积是2250平方厘米。
(2)至少需要铁丝的长度:
(30+15+25)×4
=(45+25)×4
=70×4
=280(厘米)
答:至少需要280厘米的铁丝。
10.(2025春 鼓楼区期末)一段方钢,长2.5米,横截面是边长为3厘米的正方形。已知1立方厘米的方钢重7.8克,这段方钢重多少千克?
【解答】解:先把方钢的长度换算成用厘米作单位。
2.5米=250厘米
3×3×250×7.8
=9×250×7.8
=2250×7.8
=17550(克)
17550克=17.55千克
答:这段方钢重17.55千克。
11.(2025春 鼓楼区期末)有一个无水的观赏鱼缸(如图),里面放有一块高为38厘米的假山石。如果水龙头以每分钟12升的流量向鱼缸内注水,3.45分钟后恰好将假山石完全淹没,那么假山石的体积是多少?
【解答】解:12升=12000毫升
12000毫升=12000立方厘米
48×25×38﹣12000×3.45
=1200×38﹣41400
=45600﹣41400
=4200(立方厘米)
答:假山石的体积是4200立方厘米。
12.(2025春 甘井子区期末)李老师用铁丝制作了一个长25cm,宽15cm,高2dm的长方体框架。如果用这根铁丝围成一个正方体,正方体的体积是多少立方分米?
【解答】解:(2.5+1.5+2)×4÷12
=6×4÷12
=2(分米)
2×2×2
=4×2
=8(立方分米)
答:正方体的体积是8立方分米。
13.(2025春 怀宁县期末)浩浩用一根铁丝做了一个棱长是6厘米的正方体框架,如果用这根铁丝做成长8厘米、宽5厘米的长方体框架,那么这个长方体的高是多少?体积是多少?
【解答】解:6×12÷4﹣(8+5)
=72÷4﹣13
=18﹣13
=5(厘米)
8×5×5=200(立方厘米)
答:这个长方体的高是5厘米,体积是200立方厘米。
14.(2024秋 包河区期末)如图,科学实验小组的同学们准备了大小不同的三个正方体水培花瓶。他们把两堆鹅卵石分别完全浸没在①号、②号两个正方体水培花瓶的水里,两个花瓶的水面分别上升了4厘米和8厘米。如果把这两堆鹅卵石都完全浸没在③号花瓶的水里,那么③号花瓶的水面会升高多少厘米?
【解答】解:(10×10×4+20×20×8)÷(30×30)
=3600÷900
=4(厘米)
答:把这两堆鹅卵石都完全浸没在③号花瓶的水里,那么③号花瓶的水面会升高4厘米。
15.(2025春 永昌县期末)一个长方体鱼缸,从内部量长6dm,宽4dm,高3dm,水深2dm。放入一块珊瑚石后,水面上升到2.5dm。珊瑚石的体积是多少?
【解答】解:6×4×(2.5﹣2)
=24×0.5
=12(立方分米)
答:珊瑚石的体积是12立方分米。
16.(2025春 怀宁县期末)如图,把一张正方形铁皮沿虚线折叠,围成一个长方体的侧面。给这个长方体配一个底面,这个长方体的容积是多少毫升?
【解答】解:24÷4=6(厘米)
6×6×24
=36×24
=864(立方厘米)
864立方厘米=864毫升
答:这个长方体的容积是864毫升。
17.(2024秋 金水区期末)一根长5米的长方体通气管的横截面是边长2分米的正方形。每根通气管所占空间是多少?制作4根这样的通气管,要想给这些管子刷漆(里面不刷),一共要刷多少平方米?
【解答】解:5米=50分米
2×2×50=200(立方分米)
2×50×4×4
=100×16
=1600(平方分米)
1600平方分米=16平方米
答:每根通气管所占空间200立方分米,一共要刷16平方米。
18.(2025春 福州期末)俗语说“要致富,先修路”,一个地方交通的便利对经济发展的作用是不言自明的,交通便利了,有利于地方与外界的物质与人员输入与输出,扩大交流,聚集地方人气,增加城市名气,人口增长,进而加快地方城市化进程,各个产业部门才有进一步发展的可能,扩大城市辐射范围。A市为了促进城市发展,需要修筑一些路面,某工程队接到一项修路任务后,准备用120立方米的沙子铺成一条宽5米的小路,沙子铺1分米厚,这条小路可以铺多长?
【解答】解:1分米=0.1米
120÷5÷0.1
=24÷0.1
=240(米)
答:这条小路可以铺240米长。
19.(2025春 瑞安市期末)一个长方体玻璃缸,从里面量长4dm,宽3dm,高4dm,里面装有2dm深的水,如果在玻璃缸内放入一个棱长3dm的正方体铁块,完全浸没后,那么水将会溢出多少升?
【解答】解:4﹣2=2(dm)
4×3×2=24(立方分米)
3×3×3=27(立方分米)
27﹣24=3(立方分米)
3立方分米=3L
答:水将会溢出3升。
20.(2025春 碑林区期末)用如图所示的五块长方形的亚克力板可以制作一个无盖的长方体。将这个长方体装满水,再倒一部分到一个棱长为2dm的正方体容器中,使得两个容器中的水面同样高,这时两个容器中的水面高度是多少分米?(容器壁厚度忽略不计)
【解答】解:3×2×1÷(3×2+2×2)
=6÷10
=0.6(分米)
答:这时两个容器中的水面高度是0.6分米。
21.(2025 北碚区)一个高1米的直柱体容器如图1所示,俯视图如图2所示(单位:分米)。容器中有甲、乙两块挡板(挡板的体积忽略不计)将容器分成A、B、C三个区域,其中甲挡板高6分米,乙挡板高8分米。往C区域匀速注水,10分钟后,B区域水的高度是3分米。
(1)每分钟注水多少升?
(2)如果往C区域注水的同时以同样的速度往A区域注水,多少分钟后,A区域水的高度是B区域的2倍?
【解答】解:(1)2×4×6+2×2×3
=8×6+4×3
=48+12
=60(立方分米)
60立方分米=60升
60÷10=6(升)
答:每分钟注水6升。
(2)2×4×6÷6
=8×6÷6
=8(分钟)
6×8÷(2×6)
=48÷12
=4(分米)
设还需t分钟,A区域水位是B区域的2倍,
t=1.6
8+1.6=9.6(分钟)
答:9.6分钟后,A区域水位是B区域的2倍。
21世纪教育网 www.21cnjy.com 精品试卷·第 2 页 (共 2 页)
21世纪教育网(www.21cnjy.com)
同课章节目录
