期末真题重组练习卷-2024-2025学年高中数学人教版(2019)必修第二册(含解析)
文档属性
| 名称 | 期末真题重组练习卷-2024-2025学年高中数学人教版(2019)必修第二册(含解析) |  | |
| 格式 | docx | ||
| 文件大小 | 699.0KB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 人教A版(2019) | ||
| 科目 | 数学 | ||
| 更新时间 | 2025-05-30 15:27:18 | ||
图片预览




文档简介
中小学教育资源及组卷应用平台
期末真题重组练习卷-2024-2025学年高中数学人教版(2019)必修第二册
一.选择题(共8小题)
1.(2023秋 道里区校级期末)若,则实数m=( )
A.6 B.﹣6 C.3 D.﹣3
2.(2024秋 锦州期末)已知A,B是相互独立事件,且,则P(AB)=( )
A.0.1 B.0.12 C.0.18 D.0.28
3.(2021春 海原县校级期末)设复数z满足(1+i)z=4i,则|z|=( )
A. B. C.2 D.
4.(2024秋 嘉定区校级期末)已知l,m,n是三条不重合的直线,α,β,γ是三个不重合的平面,则下列结论正确的是( )
A.若α∥β,β∥γ,则α∥γ
B.若l α,m α,l∥β,m∥β,则α∥β
C.若l∥α,l∥β,则α∥β
D.若l∥m,m α,则l∥α
5.(2024秋 海口期末)已知O是平行四边形ABCD所在平面内一点,且AB=2,AD=1,则有( )
A. B.
C. D.
6.(2024秋 景德镇期末)如图,矩形O′A′B′C′是用斜二测画法画出的水平放置的一个平面四边形OABC的直观图,其中O′A′=4,O′C′=1,那么 OABC的面积为( )
A.4 B. C.8 D.
7.(2024秋 和平区期末)在正方体ABCD﹣A1B1C1D1中,M是棱AB上的点,且AMAB,平面MCD1将此正方体分为两部分,设两部分体积分别为V1和V2(V1<V2),则( )
A. B. C. D.
8.(2024秋 通州区期末)如图某实心零部件的形状是正四棱台,已知AB=10cm,A1B1=20cm,棱台的高为12cm,先需要对该零部件的表面进行防腐处理,若每平方厘米的防腐处理费用为0.5元,则该零部件的防腐处理费用是( )
A.640元 B.440元 C.390元 D.347.5元
二.多选题(共3小题)
(多选)9.(2024秋 随州期末)下列命题正确的是( )
A.零向量是唯一没有方向的向量
B.零向量的长度等于0
C.若都为非零向量,则使成立的条件是与反向共线
D.若,,则
(多选)10.(2024秋 江阳区校级期末)抛掷一枚质地均匀的骰子,观察向上的面的点数,“点数为奇数”记为事件A,“点数小于5”记为事件B,“点数大于5”记为事件C.下列说法正确的是( )
A.A与C互斥 B.B与C对立
C.A与B相互独立 D.P(A∪B)=P(A)+P(B)
(多选)11.(2024秋 许昌期末)若正方体ABCD﹣A1B1C1D1的棱长为1,P为棱BB1的中点,点Q满足,其中λ∈[0,1],μ∈[0,1],则下列说法中正确的是( )
A.三棱锥A1﹣DQD1的体积为
B.若D1Q∥平面A1PD,则动点Q的轨迹长度为
C.至少存在一个Q点,使QD1⊥平面DA1P
D.若直线D1Q与平面BCC1B1所成角的正切值为2,则点Q轨迹的长度为
三.填空题(共3小题)
12.(2019秋 杨浦区校级期末)已知复数(a+3i)(1+2i)是纯虚数,则实数a的值为 .
13.(2024秋 上海校级期末)某高中的三个年级共有学生1000人,其中高一300人,高二340人,高三360人,该校现在要了解学生对校本课程的看法,准备从全校学生中抽取50人进行访谈,若采取分层抽样,且按年级来分层,则高一年级应抽取的人数是 .
14.(2024秋 仁寿县校级期末)一个圆台上、下底面的半径分别为3cm和8cm,若两底面圆心的连线长为12cm,则这个圆台的母线长为 cm.
四.解答题(共5小题)
15.(2023秋 武昌区期末)已知a,b,c分别为△ABC的内角A,B,C的对边,且c(acosB﹣bsinA)=a2﹣b2.
(1)求A;
(2)若a=2,△ABC的面积为2,求b+c.
16.(2024秋 丹东期末)甲乙两人进行投篮比赛,规定:每人每轮投球一次,若同时命中或同时未命中,则进行下一轮投球,若只有一人命中时,则命中者获得比赛的胜利,同时比赛结束.已知甲的命中率为,乙的命中率为,且各次投篮互不影响.
(1)求第一轮比赛未分出胜负的概率;
(2)求甲在第3轮比赛时获胜的概率.
17.(2024秋 南宁期末)已知平面向量.
(1)若,求的值;
(2)若,求的值;
(3)若向量,若与共线,求.
18.(2024秋 鄂尔多斯期末)如图,在平面四边形ABCD中,∠D=2∠B,CD=3AD=3,BC,cosB.
(1)求四边形ABCD的周长;
(2)求四边形ABCD的面积.
19.(2024秋 杭州校级期末)在直四棱柱ABCD﹣A1B1C1D1中,底面ABCD是菱形,∠DAB=60°,且AA1=AB=2,M为AD的中点,动点P满足,且x,y∈[0,1].
(1)若时,求证:AP⊥BD1;
(2)若x=y,E为A1M上一动点,且EP∥平面ABCD,求EP的最小值;
(3)若y=2x(x≠0),点O为三棱锥P﹣MBD外接球的球心,求OP的取值范围.
期末真题重组练习卷-2024-2025学年高中数学人教版(2019)必修第二册
参考答案与试题解析
一.选择题(共8小题)
题号 1 2 3 4 5 6 7 8
答案 B C D A D D D A
二.多选题(共3小题)
题号 9 10 11
答案 BCD AC ABD
一.选择题(共8小题)
1.(2023秋 道里区校级期末)若,则实数m=( )
A.6 B.﹣6 C.3 D.﹣3
【解答】解:∵||=||,
∴2 2 ,
∴ 0,又(1,2),(m,3),
∴1×m+2×3=0,解得m=﹣6.
故选:B.
2.(2024秋 锦州期末)已知A,B是相互独立事件,且,则P(AB)=( )
A.0.1 B.0.12 C.0.18 D.0.28
【解答】解:∵A,B是相互独立事件,且,
∴,
∴P(AB)=P(A)P(B)=0.3×0.6=0.18.
故选:C.
3.(2021春 海原县校级期末)设复数z满足(1+i)z=4i,则|z|=( )
A. B. C.2 D.
【解答】解:由(1+i)z=4i,
得z2+2i,
则|z|2 .
故选:D.
4.(2024秋 嘉定区校级期末)已知l,m,n是三条不重合的直线,α,β,γ是三个不重合的平面,则下列结论正确的是( )
A.若α∥β,β∥γ,则α∥γ
B.若l α,m α,l∥β,m∥β,则α∥β
C.若l∥α,l∥β,则α∥β
D.若l∥m,m α,则l∥α
【解答】解:对于A选项,由平行的传递性可知A选项成立;
对于B选项,直线l,m不一定相交,根据面面平行的判定定理易知面面平行不一定成立,错;
对于C选项,α与β也有可能相交,错;
对于D选项,直线l不一定在平面α外,也可能在面α内,故不成立,错.
故选:A.
5.(2024秋 海口期末)已知O是平行四边形ABCD所在平面内一点,且AB=2,AD=1,则有( )
A. B.
C. D.
【解答】解:对于A,当O为AB中点时,,此时不成立,故A项错误;
对于B,在平行四边形ABCD中,,
因为,所以,故B项错误;
对于C, () ()12﹣22=﹣3,故C项错误;
对于D,,故D项正确.
故选:D.
6.(2024秋 景德镇期末)如图,矩形O′A′B′C′是用斜二测画法画出的水平放置的一个平面四边形OABC的直观图,其中O′A′=4,O′C′=1,那么 OABC的面积为( )
A.4 B. C.8 D.
【解答】解:根据题意,直观图矩形O′A′B′C′的面积S′=O′A′ O′C′=4×1=4,
则原图面积S=2S′.
故选:D.
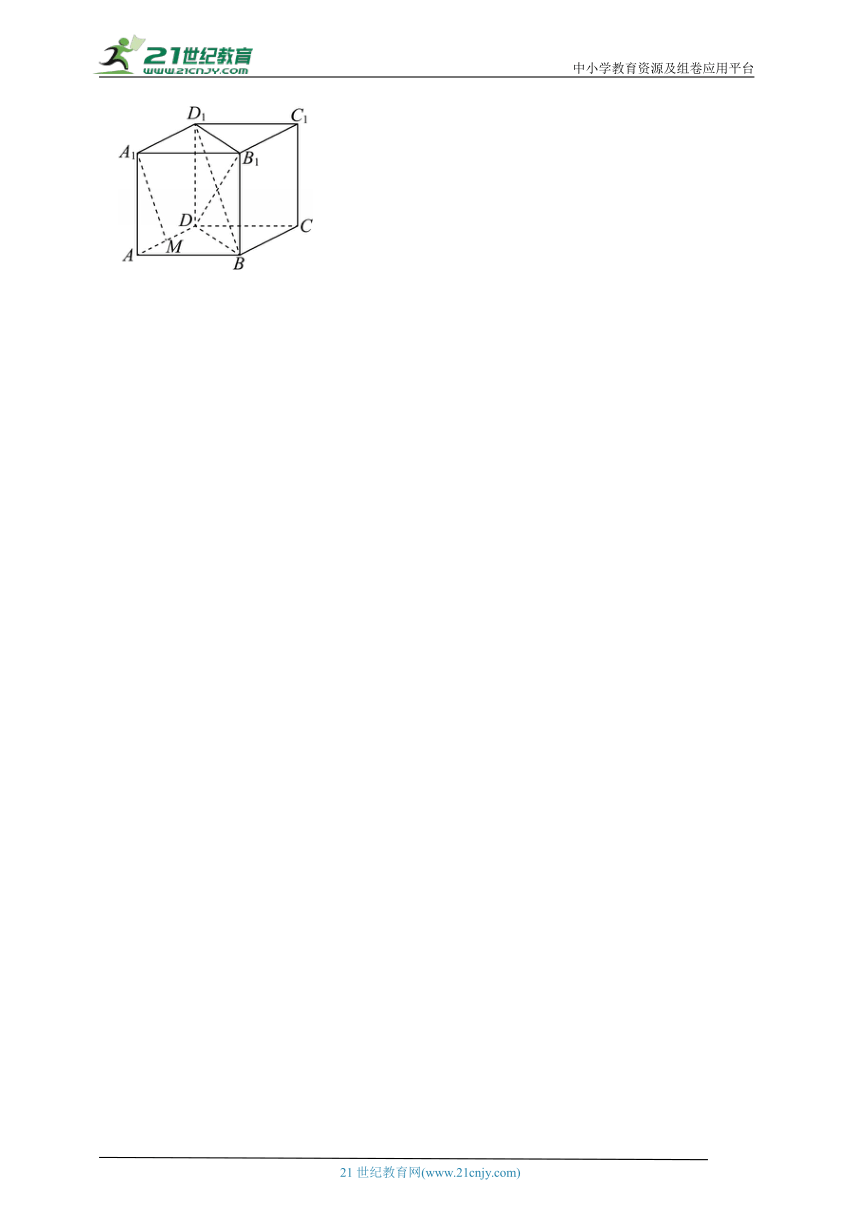
7.(2024秋 和平区期末)在正方体ABCD﹣A1B1C1D1中,M是棱AB上的点,且AMAB,平面MCD1将此正方体分为两部分,设两部分体积分别为V1和V2(V1<V2),则( )
A. B. C. D.
【解答】解:如图,取A1A的靠近A的四等分点,易得MN∥BA1∥CD1,
∴平面MCD1截正方体所得截面为等腰梯形D1CMN,
设正方体的棱长为4,
∴V114,
∴50,
∴.
故选:D.
8.(2024秋 通州区期末)如图某实心零部件的形状是正四棱台,已知AB=10cm,A1B1=20cm,棱台的高为12cm,先需要对该零部件的表面进行防腐处理,若每平方厘米的防腐处理费用为0.5元,则该零部件的防腐处理费用是( )
A.640元 B.440元 C.390元 D.347.5元
【解答】解:因为正四棱台A1B1C1D1﹣ABCD中,AB=10cm,A1B1=20cm,棱台的高为12cm,
则斜高cm,
所以195cm2,
所以4×195=780cm2,
又,,
所以S表=S侧+S上+S下=1280cm2,
又因为每平方厘米的防腐处理费用为0.5元,
所以总费用为1280×0.5=640元.
故选:A.
二.多选题(共3小题)
(多选)9.(2024秋 随州期末)下列命题正确的是( )
A.零向量是唯一没有方向的向量
B.零向量的长度等于0
C.若都为非零向量,则使成立的条件是与反向共线
D.若,,则
【解答】解:对于A,零向量是有方向的,其方向是任意的,故A错误;
对于B,由零向量的定义知,零向量的长度为0,故B正确;
对于C,因为,都是单位向量,
所以当且仅当与是相反向量,即与反向共线时才成立,故C正确;
对于D,由向量相等的定义知,,,则成立,故D正确.
故选:BCD.
(多选)10.(2024秋 江阳区校级期末)抛掷一枚质地均匀的骰子,观察向上的面的点数,“点数为奇数”记为事件A,“点数小于5”记为事件B,“点数大于5”记为事件C.下列说法正确的是( )
A.A与C互斥 B.B与C对立
C.A与B相互独立 D.P(A∪B)=P(A)+P(B)
【解答】解:抛掷一枚质地均匀的骰子,观察向上的面的点数,
“点数为奇数”记为事件A,“点数小于5”记为事件B,“点数大于5”记为事件C,
∴事件A={1,3,5},事件B={1,2,3,4},事件C={6},
对于A,事件A,C没有公共元素,不可能同时发生,A与C互斥,A正确;
对于B,事件B,C可以同时不发生,如点数5,B与C不对立,B错误;
对于C,,
P(AB)=P(A)P(B),A与B相互独立,C正确;
对于D,由选项C知,P(AB)≠0,则P(A∪B)≠P(A)+P(B),D错误.
故选:AC.
(多选)11.(2024秋 许昌期末)若正方体ABCD﹣A1B1C1D1的棱长为1,P为棱BB1的中点,点Q满足,其中λ∈[0,1],μ∈[0,1],则下列说法中正确的是( )
A.三棱锥A1﹣DQD1的体积为
B.若D1Q∥平面A1PD,则动点Q的轨迹长度为
C.至少存在一个Q点,使QD1⊥平面DA1P
D.若直线D1Q与平面BCC1B1所成角的正切值为2,则点Q轨迹的长度为
【解答】解:若正方体ABCD﹣A1B1C1D1的棱长为1,P为棱BB1的中点,点Q满足,其中λ∈[0,1],μ∈[0,1],
对于A,由题意可作图如下:
由点Q满足,其中λ∈[0,1],μ∈[0,1],则点Q∈平面BCC1B1,
由平面BCC1B1∥平面AA1D1D,
则点Q到平面A1DD1的距离h=1,
所以三棱锥A1﹣DQD1的体积,故A正确;
对于B,分别取BC,CC1,B1C1的中点为O,E,F,连接PO,DO,FE,D1F,D1E,如下图:
在正方体ABCD﹣A1B1C1D1中,E,F,P,O分别为CC1,B1C1,BB1,BC的中点,
易知PO∥A1D,FE∥PO,D1F∥DO,
因为PO∥A1D,所以A1,P,O,D共面,即PO,DO 平面A1PD,
因为FF∥PO,PO 平面A1PD,EF 平面A1PD,
所以EF∥平面A1PD,
同理可得D1F∥平面A1PD,又因为D1F∩EF=F,且D1F,EF 平面D1EF,
所以平面A1PD∥平面D1EF,由图可知平面A1PD∩平面D1EF=EF,
由A可知Q∈平面BCC1B1,当Q∈EF时,D1Q 平面D1EF,
则D1Q∥平面A1PD,
所以EF为动点Q的轨迹,易知,故B正确;
对于C,由题意可作图如下:
设,以其为一组基底,
易知,
则,,,
,
假设D1Q⊥平面A1PD,
则,
则,
则,
解得,显然不符合题意,故C错误;
对于D,由题意作图如下:
在正方体ABCD﹣A1B1C1D1中,易知D1C1⊥平面BCC1B1,
则∠D1QC1为直线D1Q与平面BCC1B1所成角,
在Rt△D1C1Q中,,可得,解得,
所以Q的轨迹为以C1为圆心,以为半径的圆弧,可得其长度为.故D正确.
故选:ABD.
三.填空题(共3小题)
12.(2019秋 杨浦区校级期末)已知复数(a+3i)(1+2i)是纯虚数,则实数a的值为 6 .
【解答】解:复数(a+3i)(1+2i)=a﹣6+(3+2a)i是纯虚数,
则a﹣6=0,3+2a≠0,解得a=6.
故答案为:6.
13.(2024秋 上海校级期末)某高中的三个年级共有学生1000人,其中高一300人,高二340人,高三360人,该校现在要了解学生对校本课程的看法,准备从全校学生中抽取50人进行访谈,若采取分层抽样,且按年级来分层,则高一年级应抽取的人数是 15 .
【解答】解:某高中的三个年级共有学生1000人,其中高一300人,高二340人,高三360人,
该校现在要了解学生对校本课程的看法,准备从全校学生中抽取50人进行访谈,
采取分层抽样,且按年级来分层,
由题意可知抽样比为:,
∴高一年级应抽取的人数是.
故答案为:15.
14.(2024秋 仁寿县校级期末)一个圆台上、下底面的半径分别为3cm和8cm,若两底面圆心的连线长为12cm,则这个圆台的母线长为 13 cm.
【解答】解:由题意,∵圆台上、下底面的半径分别为3cm和8cm,两底面圆心的连线长为12cm,
∴圆台的母线长为13cm.
故答案为13.
四.解答题(共5小题)
15.(2023秋 武昌区期末)已知a,b,c分别为△ABC的内角A,B,C的对边,且c(acosB﹣bsinA)=a2﹣b2.
(1)求A;
(2)若a=2,△ABC的面积为2,求b+c.
【解答】解:(1)由余弦定理及c(acosB﹣bsinA)=a2﹣b2,得,
整理得,
因为A∈(0,π),
所以sinA>0,
所以cosA>0,
所以tanA=1,即.
(2)因为a=2,,△ABC的面积为2bcsinAbc,
所以bc=4,
由余弦定理得,a2=b2+c2﹣2bccosA,
所以4=b2+c2bc=(b+c)2﹣2bcbc=(b+c)2﹣88,
所以(b+c)2=12+8,解得b+c=22.
16.(2024秋 丹东期末)甲乙两人进行投篮比赛,规定:每人每轮投球一次,若同时命中或同时未命中,则进行下一轮投球,若只有一人命中时,则命中者获得比赛的胜利,同时比赛结束.已知甲的命中率为,乙的命中率为,且各次投篮互不影响.
(1)求第一轮比赛未分出胜负的概率;
(2)求甲在第3轮比赛时获胜的概率.
【解答】解:(1)根据题意,记事件Ai=“甲第i轮投中”,Bi=“乙第i轮投中”,i=1,2,3,
第一轮比赛未分出胜负是甲乙同时命中或都未命中,即事件A1B1,
则要求概率;
(2)根据题意,甲在第3轮比赛时获胜,
则前两轮都是平局,第3轮投球甲命中,即事件,
则要求概率.
17.(2024秋 南宁期末)已知平面向量.
(1)若,求的值;
(2)若,求的值;
(3)若向量,若与共线,求.
【解答】解:(1)已知平面向量.
因为,
所以,
则1×6+3x=0,
解得x=﹣2,
故,
则(2,6)﹣(18,﹣6)=(﹣16,12).
(2)因为,
所以x=3×6=18,
则,.
(3),,
若与共线,
则5×(3+x)=7×(x+1),
解得x=4,
即,
故.
18.(2024秋 鄂尔多斯期末)如图,在平面四边形ABCD中,∠D=2∠B,CD=3AD=3,BC,cosB.
(1)求四边形ABCD的周长;
(2)求四边形ABCD的面积.
【解答】解:(1)由,∠D=2∠B,可得,
在△ACD中,.
所以在△ABC中,AC2=AB2+BC2﹣2AB BCcosB=12,
即AB2+6﹣2AB 12,整理得,解得(舍负).
所以四边形ABCD的周长AB+BC+CD+DA.
(2)根据,B∈(0,),可得sinB,
所以S△ABCAB×BC×sinB.
由,D∈(0,π),可得,
所以S△ADCAD×DC×sinD,
可得四边形ABCD的面积S=S△ABC+S△ADC.
19.(2024秋 杭州校级期末)在直四棱柱ABCD﹣A1B1C1D1中,底面ABCD是菱形,∠DAB=60°,且AA1=AB=2,M为AD的中点,动点P满足,且x,y∈[0,1].
(1)若时,求证:AP⊥BD1;
(2)若x=y,E为A1M上一动点,且EP∥平面ABCD,求EP的最小值;
(3)若y=2x(x≠0),点O为三棱锥P﹣MBD外接球的球心,求OP的取值范围.
【解答】解:(1)证明:在直四棱柱ABCD﹣A1B1C1D1中,底面ABCD是菱形,∠DAB=60°,且AA1=AB=2,
M为AD的中点,动点P满足xy,x,y∈[0,1].
在底面菱形ABCD中,连接AC,
记AC∩BD=O′,取B1D1的中点为Q,连接OQ,
由菱形ABCD的性质得AC⊥BD,在直四棱柱ABCD﹣A1B1C1D1中,知QO′⊥平面ABCD,
∵AC,BD 平面ABCD,∴O′Q⊥AC,O′Q⊥BD,∴O′A,O′B,O′Q两两垂直,
以O′为坐标原点,分别以O′A,O′B,O′Q所在直线为x,y,z轴,建立空间直角坐标系,如图,
∵∠DAB=60°,∴OBAB=1,OAAB,
可得,
则,
∴,则,
由,则,即,
∵,∴,则AP⊥BD1.
(2)x=y,E为A1M上一动点,且EP∥平面ABCD,由题意作图如下:
由图可知平面ABCD的一个法向量,
由,则AD的中点M的坐标为,
即,由E∈A1M,则(0≤λ≤1),
由(1)可知,由x=y,则,
则,
由EP∥平面ABCD,则,解得x=1﹣λ,
∴,
则由向量的模的性质得,
当时,等号成立,∴EP的最小值为.
(3)y=2x(x≠0),点O为三棱锥P﹣MBD外接球的球心,由题意作图如下:
由(1)可得,由y=2x(x≠0),则(0,﹣4x,2x),
设BP的中点为N,则(0,﹣2x,x),
在菱形ABCD中∠DAB=60°,且M为AD中点,则BM⊥AD,
在三棱锥P﹣MBD中,底面Rt△MBD的外接圆圆心为BD的中点O′,
由题意知球心O为线段BP的中垂线与直线O′Q的交点,则设O(0,0,μ),
由B(0,1,0),则,(0,1﹣2x,x﹣μ),
由题意知0,可得﹣4x+8x2+2x2﹣2xμ=0,解得μ=2﹣5x,
由x∈(0,1],y∈(0,1],则x∈(0,],即μ∈(,2],
∴OP=||∈[1,),
∴OP的取值范围是[1,).
21世纪教育网 www.21cnjy.com 精品试卷·第 2 页 (共 2 页)
21世纪教育网(www.21cnjy.com)
期末真题重组练习卷-2024-2025学年高中数学人教版(2019)必修第二册
一.选择题(共8小题)
1.(2023秋 道里区校级期末)若,则实数m=( )
A.6 B.﹣6 C.3 D.﹣3
2.(2024秋 锦州期末)已知A,B是相互独立事件,且,则P(AB)=( )
A.0.1 B.0.12 C.0.18 D.0.28
3.(2021春 海原县校级期末)设复数z满足(1+i)z=4i,则|z|=( )
A. B. C.2 D.
4.(2024秋 嘉定区校级期末)已知l,m,n是三条不重合的直线,α,β,γ是三个不重合的平面,则下列结论正确的是( )
A.若α∥β,β∥γ,则α∥γ
B.若l α,m α,l∥β,m∥β,则α∥β
C.若l∥α,l∥β,则α∥β
D.若l∥m,m α,则l∥α
5.(2024秋 海口期末)已知O是平行四边形ABCD所在平面内一点,且AB=2,AD=1,则有( )
A. B.
C. D.
6.(2024秋 景德镇期末)如图,矩形O′A′B′C′是用斜二测画法画出的水平放置的一个平面四边形OABC的直观图,其中O′A′=4,O′C′=1,那么 OABC的面积为( )
A.4 B. C.8 D.
7.(2024秋 和平区期末)在正方体ABCD﹣A1B1C1D1中,M是棱AB上的点,且AMAB,平面MCD1将此正方体分为两部分,设两部分体积分别为V1和V2(V1<V2),则( )
A. B. C. D.
8.(2024秋 通州区期末)如图某实心零部件的形状是正四棱台,已知AB=10cm,A1B1=20cm,棱台的高为12cm,先需要对该零部件的表面进行防腐处理,若每平方厘米的防腐处理费用为0.5元,则该零部件的防腐处理费用是( )
A.640元 B.440元 C.390元 D.347.5元
二.多选题(共3小题)
(多选)9.(2024秋 随州期末)下列命题正确的是( )
A.零向量是唯一没有方向的向量
B.零向量的长度等于0
C.若都为非零向量,则使成立的条件是与反向共线
D.若,,则
(多选)10.(2024秋 江阳区校级期末)抛掷一枚质地均匀的骰子,观察向上的面的点数,“点数为奇数”记为事件A,“点数小于5”记为事件B,“点数大于5”记为事件C.下列说法正确的是( )
A.A与C互斥 B.B与C对立
C.A与B相互独立 D.P(A∪B)=P(A)+P(B)
(多选)11.(2024秋 许昌期末)若正方体ABCD﹣A1B1C1D1的棱长为1,P为棱BB1的中点,点Q满足,其中λ∈[0,1],μ∈[0,1],则下列说法中正确的是( )
A.三棱锥A1﹣DQD1的体积为
B.若D1Q∥平面A1PD,则动点Q的轨迹长度为
C.至少存在一个Q点,使QD1⊥平面DA1P
D.若直线D1Q与平面BCC1B1所成角的正切值为2,则点Q轨迹的长度为
三.填空题(共3小题)
12.(2019秋 杨浦区校级期末)已知复数(a+3i)(1+2i)是纯虚数,则实数a的值为 .
13.(2024秋 上海校级期末)某高中的三个年级共有学生1000人,其中高一300人,高二340人,高三360人,该校现在要了解学生对校本课程的看法,准备从全校学生中抽取50人进行访谈,若采取分层抽样,且按年级来分层,则高一年级应抽取的人数是 .
14.(2024秋 仁寿县校级期末)一个圆台上、下底面的半径分别为3cm和8cm,若两底面圆心的连线长为12cm,则这个圆台的母线长为 cm.
四.解答题(共5小题)
15.(2023秋 武昌区期末)已知a,b,c分别为△ABC的内角A,B,C的对边,且c(acosB﹣bsinA)=a2﹣b2.
(1)求A;
(2)若a=2,△ABC的面积为2,求b+c.
16.(2024秋 丹东期末)甲乙两人进行投篮比赛,规定:每人每轮投球一次,若同时命中或同时未命中,则进行下一轮投球,若只有一人命中时,则命中者获得比赛的胜利,同时比赛结束.已知甲的命中率为,乙的命中率为,且各次投篮互不影响.
(1)求第一轮比赛未分出胜负的概率;
(2)求甲在第3轮比赛时获胜的概率.
17.(2024秋 南宁期末)已知平面向量.
(1)若,求的值;
(2)若,求的值;
(3)若向量,若与共线,求.
18.(2024秋 鄂尔多斯期末)如图,在平面四边形ABCD中,∠D=2∠B,CD=3AD=3,BC,cosB.
(1)求四边形ABCD的周长;
(2)求四边形ABCD的面积.
19.(2024秋 杭州校级期末)在直四棱柱ABCD﹣A1B1C1D1中,底面ABCD是菱形,∠DAB=60°,且AA1=AB=2,M为AD的中点,动点P满足,且x,y∈[0,1].
(1)若时,求证:AP⊥BD1;
(2)若x=y,E为A1M上一动点,且EP∥平面ABCD,求EP的最小值;
(3)若y=2x(x≠0),点O为三棱锥P﹣MBD外接球的球心,求OP的取值范围.
期末真题重组练习卷-2024-2025学年高中数学人教版(2019)必修第二册
参考答案与试题解析
一.选择题(共8小题)
题号 1 2 3 4 5 6 7 8
答案 B C D A D D D A
二.多选题(共3小题)
题号 9 10 11
答案 BCD AC ABD
一.选择题(共8小题)
1.(2023秋 道里区校级期末)若,则实数m=( )
A.6 B.﹣6 C.3 D.﹣3
【解答】解:∵||=||,
∴2 2 ,
∴ 0,又(1,2),(m,3),
∴1×m+2×3=0,解得m=﹣6.
故选:B.
2.(2024秋 锦州期末)已知A,B是相互独立事件,且,则P(AB)=( )
A.0.1 B.0.12 C.0.18 D.0.28
【解答】解:∵A,B是相互独立事件,且,
∴,
∴P(AB)=P(A)P(B)=0.3×0.6=0.18.
故选:C.
3.(2021春 海原县校级期末)设复数z满足(1+i)z=4i,则|z|=( )
A. B. C.2 D.
【解答】解:由(1+i)z=4i,
得z2+2i,
则|z|2 .
故选:D.
4.(2024秋 嘉定区校级期末)已知l,m,n是三条不重合的直线,α,β,γ是三个不重合的平面,则下列结论正确的是( )
A.若α∥β,β∥γ,则α∥γ
B.若l α,m α,l∥β,m∥β,则α∥β
C.若l∥α,l∥β,则α∥β
D.若l∥m,m α,则l∥α
【解答】解:对于A选项,由平行的传递性可知A选项成立;
对于B选项,直线l,m不一定相交,根据面面平行的判定定理易知面面平行不一定成立,错;
对于C选项,α与β也有可能相交,错;
对于D选项,直线l不一定在平面α外,也可能在面α内,故不成立,错.
故选:A.
5.(2024秋 海口期末)已知O是平行四边形ABCD所在平面内一点,且AB=2,AD=1,则有( )
A. B.
C. D.
【解答】解:对于A,当O为AB中点时,,此时不成立,故A项错误;
对于B,在平行四边形ABCD中,,
因为,所以,故B项错误;
对于C, () ()12﹣22=﹣3,故C项错误;
对于D,,故D项正确.
故选:D.
6.(2024秋 景德镇期末)如图,矩形O′A′B′C′是用斜二测画法画出的水平放置的一个平面四边形OABC的直观图,其中O′A′=4,O′C′=1,那么 OABC的面积为( )
A.4 B. C.8 D.
【解答】解:根据题意,直观图矩形O′A′B′C′的面积S′=O′A′ O′C′=4×1=4,
则原图面积S=2S′.
故选:D.
7.(2024秋 和平区期末)在正方体ABCD﹣A1B1C1D1中,M是棱AB上的点,且AMAB,平面MCD1将此正方体分为两部分,设两部分体积分别为V1和V2(V1<V2),则( )
A. B. C. D.
【解答】解:如图,取A1A的靠近A的四等分点,易得MN∥BA1∥CD1,
∴平面MCD1截正方体所得截面为等腰梯形D1CMN,
设正方体的棱长为4,
∴V114,
∴50,
∴.
故选:D.
8.(2024秋 通州区期末)如图某实心零部件的形状是正四棱台,已知AB=10cm,A1B1=20cm,棱台的高为12cm,先需要对该零部件的表面进行防腐处理,若每平方厘米的防腐处理费用为0.5元,则该零部件的防腐处理费用是( )
A.640元 B.440元 C.390元 D.347.5元
【解答】解:因为正四棱台A1B1C1D1﹣ABCD中,AB=10cm,A1B1=20cm,棱台的高为12cm,
则斜高cm,
所以195cm2,
所以4×195=780cm2,
又,,
所以S表=S侧+S上+S下=1280cm2,
又因为每平方厘米的防腐处理费用为0.5元,
所以总费用为1280×0.5=640元.
故选:A.
二.多选题(共3小题)
(多选)9.(2024秋 随州期末)下列命题正确的是( )
A.零向量是唯一没有方向的向量
B.零向量的长度等于0
C.若都为非零向量,则使成立的条件是与反向共线
D.若,,则
【解答】解:对于A,零向量是有方向的,其方向是任意的,故A错误;
对于B,由零向量的定义知,零向量的长度为0,故B正确;
对于C,因为,都是单位向量,
所以当且仅当与是相反向量,即与反向共线时才成立,故C正确;
对于D,由向量相等的定义知,,,则成立,故D正确.
故选:BCD.
(多选)10.(2024秋 江阳区校级期末)抛掷一枚质地均匀的骰子,观察向上的面的点数,“点数为奇数”记为事件A,“点数小于5”记为事件B,“点数大于5”记为事件C.下列说法正确的是( )
A.A与C互斥 B.B与C对立
C.A与B相互独立 D.P(A∪B)=P(A)+P(B)
【解答】解:抛掷一枚质地均匀的骰子,观察向上的面的点数,
“点数为奇数”记为事件A,“点数小于5”记为事件B,“点数大于5”记为事件C,
∴事件A={1,3,5},事件B={1,2,3,4},事件C={6},
对于A,事件A,C没有公共元素,不可能同时发生,A与C互斥,A正确;
对于B,事件B,C可以同时不发生,如点数5,B与C不对立,B错误;
对于C,,
P(AB)=P(A)P(B),A与B相互独立,C正确;
对于D,由选项C知,P(AB)≠0,则P(A∪B)≠P(A)+P(B),D错误.
故选:AC.
(多选)11.(2024秋 许昌期末)若正方体ABCD﹣A1B1C1D1的棱长为1,P为棱BB1的中点,点Q满足,其中λ∈[0,1],μ∈[0,1],则下列说法中正确的是( )
A.三棱锥A1﹣DQD1的体积为
B.若D1Q∥平面A1PD,则动点Q的轨迹长度为
C.至少存在一个Q点,使QD1⊥平面DA1P
D.若直线D1Q与平面BCC1B1所成角的正切值为2,则点Q轨迹的长度为
【解答】解:若正方体ABCD﹣A1B1C1D1的棱长为1,P为棱BB1的中点,点Q满足,其中λ∈[0,1],μ∈[0,1],
对于A,由题意可作图如下:
由点Q满足,其中λ∈[0,1],μ∈[0,1],则点Q∈平面BCC1B1,
由平面BCC1B1∥平面AA1D1D,
则点Q到平面A1DD1的距离h=1,
所以三棱锥A1﹣DQD1的体积,故A正确;
对于B,分别取BC,CC1,B1C1的中点为O,E,F,连接PO,DO,FE,D1F,D1E,如下图:
在正方体ABCD﹣A1B1C1D1中,E,F,P,O分别为CC1,B1C1,BB1,BC的中点,
易知PO∥A1D,FE∥PO,D1F∥DO,
因为PO∥A1D,所以A1,P,O,D共面,即PO,DO 平面A1PD,
因为FF∥PO,PO 平面A1PD,EF 平面A1PD,
所以EF∥平面A1PD,
同理可得D1F∥平面A1PD,又因为D1F∩EF=F,且D1F,EF 平面D1EF,
所以平面A1PD∥平面D1EF,由图可知平面A1PD∩平面D1EF=EF,
由A可知Q∈平面BCC1B1,当Q∈EF时,D1Q 平面D1EF,
则D1Q∥平面A1PD,
所以EF为动点Q的轨迹,易知,故B正确;
对于C,由题意可作图如下:
设,以其为一组基底,
易知,
则,,,
,
假设D1Q⊥平面A1PD,
则,
则,
则,
解得,显然不符合题意,故C错误;
对于D,由题意作图如下:
在正方体ABCD﹣A1B1C1D1中,易知D1C1⊥平面BCC1B1,
则∠D1QC1为直线D1Q与平面BCC1B1所成角,
在Rt△D1C1Q中,,可得,解得,
所以Q的轨迹为以C1为圆心,以为半径的圆弧,可得其长度为.故D正确.
故选:ABD.
三.填空题(共3小题)
12.(2019秋 杨浦区校级期末)已知复数(a+3i)(1+2i)是纯虚数,则实数a的值为 6 .
【解答】解:复数(a+3i)(1+2i)=a﹣6+(3+2a)i是纯虚数,
则a﹣6=0,3+2a≠0,解得a=6.
故答案为:6.
13.(2024秋 上海校级期末)某高中的三个年级共有学生1000人,其中高一300人,高二340人,高三360人,该校现在要了解学生对校本课程的看法,准备从全校学生中抽取50人进行访谈,若采取分层抽样,且按年级来分层,则高一年级应抽取的人数是 15 .
【解答】解:某高中的三个年级共有学生1000人,其中高一300人,高二340人,高三360人,
该校现在要了解学生对校本课程的看法,准备从全校学生中抽取50人进行访谈,
采取分层抽样,且按年级来分层,
由题意可知抽样比为:,
∴高一年级应抽取的人数是.
故答案为:15.
14.(2024秋 仁寿县校级期末)一个圆台上、下底面的半径分别为3cm和8cm,若两底面圆心的连线长为12cm,则这个圆台的母线长为 13 cm.
【解答】解:由题意,∵圆台上、下底面的半径分别为3cm和8cm,两底面圆心的连线长为12cm,
∴圆台的母线长为13cm.
故答案为13.
四.解答题(共5小题)
15.(2023秋 武昌区期末)已知a,b,c分别为△ABC的内角A,B,C的对边,且c(acosB﹣bsinA)=a2﹣b2.
(1)求A;
(2)若a=2,△ABC的面积为2,求b+c.
【解答】解:(1)由余弦定理及c(acosB﹣bsinA)=a2﹣b2,得,
整理得,
因为A∈(0,π),
所以sinA>0,
所以cosA>0,
所以tanA=1,即.
(2)因为a=2,,△ABC的面积为2bcsinAbc,
所以bc=4,
由余弦定理得,a2=b2+c2﹣2bccosA,
所以4=b2+c2bc=(b+c)2﹣2bcbc=(b+c)2﹣88,
所以(b+c)2=12+8,解得b+c=22.
16.(2024秋 丹东期末)甲乙两人进行投篮比赛,规定:每人每轮投球一次,若同时命中或同时未命中,则进行下一轮投球,若只有一人命中时,则命中者获得比赛的胜利,同时比赛结束.已知甲的命中率为,乙的命中率为,且各次投篮互不影响.
(1)求第一轮比赛未分出胜负的概率;
(2)求甲在第3轮比赛时获胜的概率.
【解答】解:(1)根据题意,记事件Ai=“甲第i轮投中”,Bi=“乙第i轮投中”,i=1,2,3,
第一轮比赛未分出胜负是甲乙同时命中或都未命中,即事件A1B1,
则要求概率;
(2)根据题意,甲在第3轮比赛时获胜,
则前两轮都是平局,第3轮投球甲命中,即事件,
则要求概率.
17.(2024秋 南宁期末)已知平面向量.
(1)若,求的值;
(2)若,求的值;
(3)若向量,若与共线,求.
【解答】解:(1)已知平面向量.
因为,
所以,
则1×6+3x=0,
解得x=﹣2,
故,
则(2,6)﹣(18,﹣6)=(﹣16,12).
(2)因为,
所以x=3×6=18,
则,.
(3),,
若与共线,
则5×(3+x)=7×(x+1),
解得x=4,
即,
故.
18.(2024秋 鄂尔多斯期末)如图,在平面四边形ABCD中,∠D=2∠B,CD=3AD=3,BC,cosB.
(1)求四边形ABCD的周长;
(2)求四边形ABCD的面积.
【解答】解:(1)由,∠D=2∠B,可得,
在△ACD中,.
所以在△ABC中,AC2=AB2+BC2﹣2AB BCcosB=12,
即AB2+6﹣2AB 12,整理得,解得(舍负).
所以四边形ABCD的周长AB+BC+CD+DA.
(2)根据,B∈(0,),可得sinB,
所以S△ABCAB×BC×sinB.
由,D∈(0,π),可得,
所以S△ADCAD×DC×sinD,
可得四边形ABCD的面积S=S△ABC+S△ADC.
19.(2024秋 杭州校级期末)在直四棱柱ABCD﹣A1B1C1D1中,底面ABCD是菱形,∠DAB=60°,且AA1=AB=2,M为AD的中点,动点P满足,且x,y∈[0,1].
(1)若时,求证:AP⊥BD1;
(2)若x=y,E为A1M上一动点,且EP∥平面ABCD,求EP的最小值;
(3)若y=2x(x≠0),点O为三棱锥P﹣MBD外接球的球心,求OP的取值范围.
【解答】解:(1)证明:在直四棱柱ABCD﹣A1B1C1D1中,底面ABCD是菱形,∠DAB=60°,且AA1=AB=2,
M为AD的中点,动点P满足xy,x,y∈[0,1].
在底面菱形ABCD中,连接AC,
记AC∩BD=O′,取B1D1的中点为Q,连接OQ,
由菱形ABCD的性质得AC⊥BD,在直四棱柱ABCD﹣A1B1C1D1中,知QO′⊥平面ABCD,
∵AC,BD 平面ABCD,∴O′Q⊥AC,O′Q⊥BD,∴O′A,O′B,O′Q两两垂直,
以O′为坐标原点,分别以O′A,O′B,O′Q所在直线为x,y,z轴,建立空间直角坐标系,如图,
∵∠DAB=60°,∴OBAB=1,OAAB,
可得,
则,
∴,则,
由,则,即,
∵,∴,则AP⊥BD1.
(2)x=y,E为A1M上一动点,且EP∥平面ABCD,由题意作图如下:
由图可知平面ABCD的一个法向量,
由,则AD的中点M的坐标为,
即,由E∈A1M,则(0≤λ≤1),
由(1)可知,由x=y,则,
则,
由EP∥平面ABCD,则,解得x=1﹣λ,
∴,
则由向量的模的性质得,
当时,等号成立,∴EP的最小值为.
(3)y=2x(x≠0),点O为三棱锥P﹣MBD外接球的球心,由题意作图如下:
由(1)可得,由y=2x(x≠0),则(0,﹣4x,2x),
设BP的中点为N,则(0,﹣2x,x),
在菱形ABCD中∠DAB=60°,且M为AD中点,则BM⊥AD,
在三棱锥P﹣MBD中,底面Rt△MBD的外接圆圆心为BD的中点O′,
由题意知球心O为线段BP的中垂线与直线O′Q的交点,则设O(0,0,μ),
由B(0,1,0),则,(0,1﹣2x,x﹣μ),
由题意知0,可得﹣4x+8x2+2x2﹣2xμ=0,解得μ=2﹣5x,
由x∈(0,1],y∈(0,1],则x∈(0,],即μ∈(,2],
∴OP=||∈[1,),
∴OP的取值范围是[1,).
21世纪教育网 www.21cnjy.com 精品试卷·第 2 页 (共 2 页)
21世纪教育网(www.21cnjy.com)
同课章节目录
- 第六章 平面向量及其应用
- 6.1 平面向量的概念
- 6.2 平面向量的运算
- 6.3 平面向量基本定理及坐标表示
- 6.4 平面向量的应用
- 第七章 复数
- 7.1 复数的概念
- 7.2 复数的四则运算
- 7.3 * 复数的三角表示
- 第八章 立体几何初步
- 8.1 基本立体图形
- 8.2 立体图形的直观图
- 8.3 简单几何体的表面积与体积
- 8.4 空间点、直线、平面之间的位置关系
- 8.5 空间直线、平面的平行
- 8.6 空间直线、平面的垂直
- 第九章 统计
- 9.1 随机抽样
- 9.2 用样本估计总体
- 9.3 统计分析案例 公司员工
- 第十章 概率
- 10.1 随机事件与概率
- 10.2 事件的相互独立性
- 10.3 频率与概率
