2.2认识有理数第1课时- 有理数 课件(共35张PPT)
文档属性
| 名称 | 2.2认识有理数第1课时- 有理数 课件(共35张PPT) |  | |
| 格式 | pptx | ||
| 文件大小 | 2.6MB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 鲁教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2025-05-30 18:04:41 | ||
图片预览







文档简介
(共35张PPT)
第二章 有理数及其运算 2.2
认识有理数
第1课时 有理数
1.由实例引出具有相反意义的量,并会表示具有相反意思的量。
2.进一步认识正数和负数,会判断一个数是正数还是负数.
3.理解有理数的意义,能按一定的标准对有理数进行分类.
学习目标
重点
重点
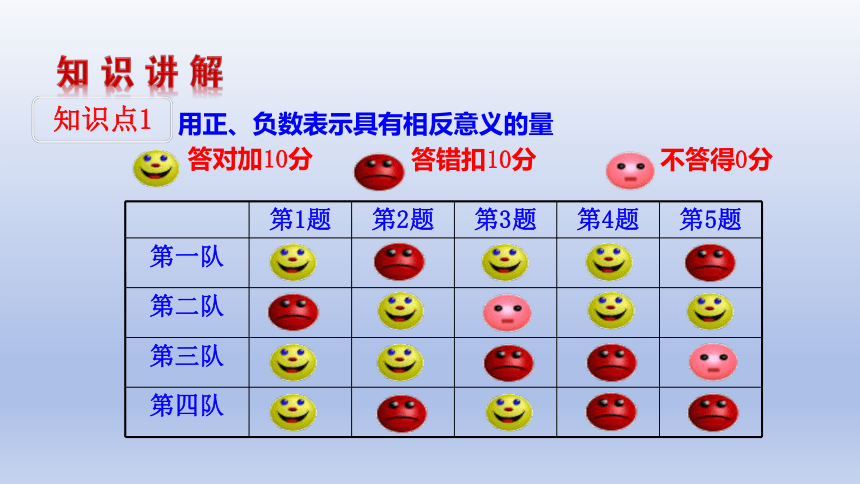
答对加10分
答错扣10分
不答得0分
第1题 第2题 第3题 第4题 第5题
第一队
第二队
第三队
第四队
用正、负数表示具有相反意义的量
知识点1
红色所表示的得
分比0分低
带“-”的得分比0分低
这里出现了比0分低的得分,我们可以用带有“-”号的数来表示,如-10(读作:负10)表示比0低10的数;
对于比0分高的得分,可以在前面加上“+”号,如+10(读作:正10)表示比0高10的数.
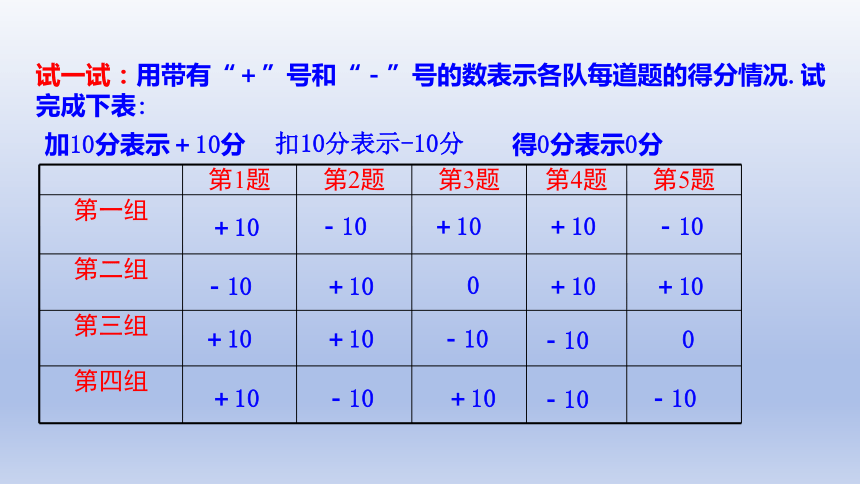
试一试:用带有“+”号和“-”号的数表示各队每道题的得分情况.试完成下表:
第1题 第2题 第3题 第4题 第5题
第一组
第二组
第三组
第四组
+10
-10
+10
+10
-10
-10
+10
0
+10
+10
+10
+10
-10
-10
0
+10
-10
+10
-10
-10
加10分表示+10分
扣10分表示-10分
得0分表示0分
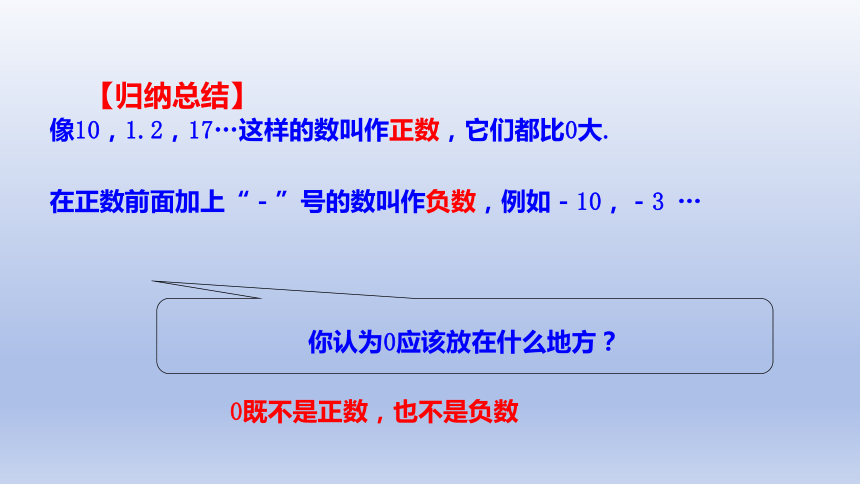
像10,1.2,17…这样的数叫作正数,它们都比0大.
在正数前面加上“-”号的数叫作负数,例如-10,-3 …
你认为0应该放在什么地方?
0既不是正数,也不是负数
【归纳总结】
新知初探
贰
探究二 有理数的分类
思考:我们学过了哪些数?请举出相应的例子。
…… 负分数
1,2,3
0
-1,-2,-3
……正整数
……零
……负整数
…… 正分数
新知初探
贰
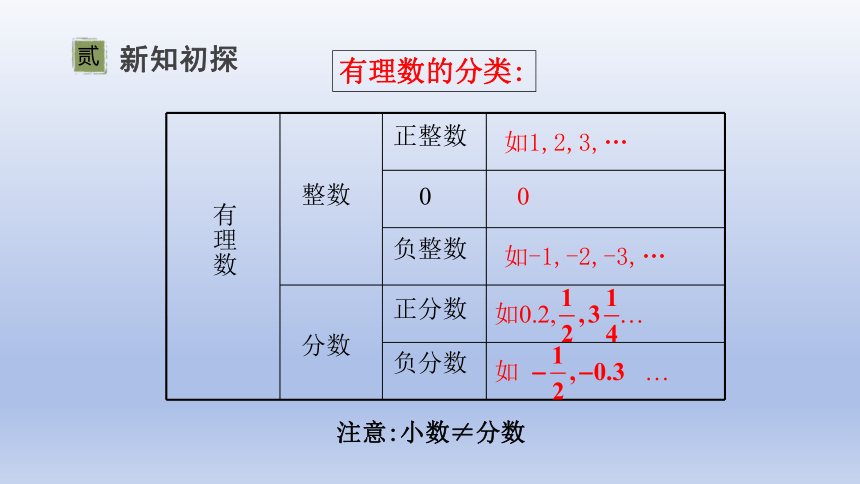
有理数的分类:
有理数
整数
分数
负分数
正分数
负整数
正整数
0
注意:小数≠分数
如1,2,3,…
0
如-1,-2,-3,…
如0.2, …
如 …
新知初探
贰
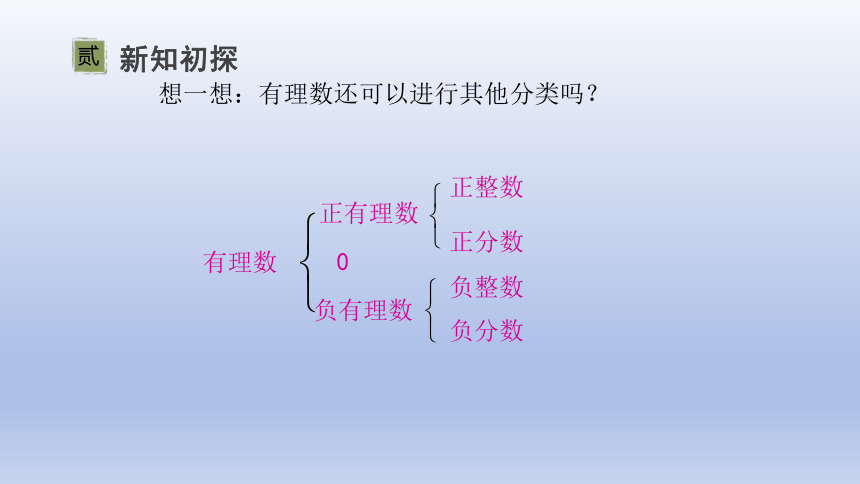
想一想:有理数还可以进行其他分类吗?
正有理数
负有理数
正分数
负分数
负整数
正整数
0
有理数
新知初探
贰
正数集合{ …};
负数集合{ …};
整数集合{ …};
正分数集合{ …};
负分数集合{ …};
分数集合{ …}.
巩固练习:把下面各数填在相应的括号里:
新知初探
贰
4.分数包括有限小数和无限循环小数。
小结
有理数的分类中的四点注意:
1.相对性:正数是相对负数而言的,整数是相对分数而言的。
2.特殊0:0既不是正数,也不是负数,但0是整数。
3.多属性:同一个数,可能属于多个不同的集合。如5既是正
数又是整数。
典例分析
例1:(1)转动转盘时,若规定顺时针转动为正,则逆时针转动5圈表示为________.
(2)若把后退规定为负,则+102米表示___________,0米表示__________.
(3)如果正午12时记作0时,午后3时记作+3时,那么上午8时记作________.
-5圈
前进102米
原地不动
-4时
例2:把下列各数填入相应的集合中:
典例分析
学以致用
1.如果收入100元记作+100元,那么支出100元记作( )
A.-100元 B.+100元 C.-200元 D.+200元
A
2.如果汽车向东行驶30米记作+30米,那么-50米表示( )
A.向东行驶50米 B.向西行驶50米 C.向南行驶50米 D.向北行驶50
3.在一次数学测试中,七(2) 班的平均分为 85 分,把高于平均分的高出部分数记为正数,老师将某一小组的美美、多多、田田、乐乐四位同学的成绩记为+7,-4,-11,+13,则这四位同学实际成绩最高的是 ( )
A.美美 B.多多 C.田田 D.乐乐
B
D
学以致用
4.下列说法中,正确的是( )
A.正整数和负整数统称整数
B.整数和分数统称有理数
C.零既可以是正整数,也可以是负整数
D.一个有理数不是正数就是负数
B
5.某食品包装袋上标有“净含量(385±5)克”,这包食品合格的净含量范围是____________.
380~390克
学以致用
-23,28,0,4
28,0,4
【变式训练】
1.(2024·东莞一模)如果温度上升10 ℃记作+10 ℃,那么温度下降7 ℃记作( )
A.+3 ℃ B.-3 ℃ C.+7 ℃ D.-7 ℃
【解析】如果温度上升10 ℃记作+10 ℃,那么温度下降7 ℃记作-7 ℃.
2.某种零件的直径合格尺寸为(5±0.1)mm,则下列零件直径合格的是( )
A.4.85 mm B.4.95 mm
C.5.11 mm D.5.15 mm
D
B
【重点2】有理数的分类(推理能力)
【典例2】(教材再开发·P25T2强化)请把下列各数填入相应的集合中:
-,-3,2,0,13.14,,10%.
负数集合{ …};
分数集合{ …}.
【自主解答】根据负数、分数的定义可得:
负数集合{-,-3,…};
分数集合{-,13.14,,10%,…}.
答案:-,-3 -,13.14,,10%
【变式训练】
1.(2024·湛江廉江一模)下列四个数中,负整数是( )
A.2 024 B.-3.14
C.0 D.-3
【解析】在2 024,-3.14,0,-3中,2 024是正整数,-3.14是负分数,0是整数,-3是负整数.
D
2.把下面各数填入图中相应的位置,并填写公共部分的名称.
-0.7,-10,+3.4,-109,-4,0,85,0.4.
【解析】根据有理数的分类法则得:
8.[2024天津和平区月考]据史料记载,早在两千多年前,中
国就有了正负数的概念,关于负数有下列4种说法:
①在某个数的前面加上符号“-”得到的数;
②不大于0的数;
③除去正数的其他数;
④在正数的前面加上符号“-”得到的数.
其中正确的是 (填序号).
④
分层练习-基础
分层练习-基础
知识点3 有理数的概念及其分类
9. 、 、 统称为整数,
与 统称为分数, 与 统称
为有理数.
正整数
零
负整数
正分数
负分数
整数
分数
10. 在π, ,-3, 这四个数中,整数是( C )
A. π B.
C. -3 D.
C
分层练习-基础
11.下列关于0的说法错误的是( A )
A. 任何情况下,0的实际意义就是什么都没有
B. 0是偶数不是奇数
C. 0既不是正数也不是负数
D. 0是整数也是有理数
A
12.把下列各数填入相应的集
合中:- ,0.618,-3.14,26,-2, ,0,
70%,-π.
正分数集合:{0.618, ,70%,…};
整数集合:{26,-2,0,…};
非负数集合:{0.618,26, ,0,70%,…};
负有理数集合:{- ,-3.14,-2,…}.
0.618, ,70%,
26,-2,0,
0.618,26, ,0,70%,
- ,-3.14,-2,
分层练习-基础
13.[2024南昌高新区月考]对于有理数:- ,1,8.6,-
7,0, ,-4 ,+101,-0.05,-9,下列说法正确
的是( D )
D
A. 只有1,-7,+101,-9是整数
B. 其中有三个数是正整数
C. 非负数有1,8.6,0,+101
D. 只有- ,-4 ,-0.05是负分数
分层练习-巩固
分层练习-巩固
14.规定45分钟为1个单位时间,并以每天上午9时记为0,9时以前的时间记为负数,9时以后的时间记为正数,例如:8:15记为-1;9:45记为+1,依此类推,则上午7:30应记为 .
-2
9. 某数学俱乐部有一种“秘密”的记账方式,当他们收入500
元时,记为-440元;当他们用去50元时,记为+110元.猜一
猜,当他们用去70元时,应记为 元.
【解析】500-440=60(元),110-50=60(元).
当他们用去70元时,应记为70+60=130(元).
故答案为+130.
+130
13. (选做)如图,一只甲虫在5×5的网格(每小格边长为1)
上沿着网格线运动.它从点 A 处出发去看望点 B , C , D 处的其
他甲虫.规定:向上、向右走为正,向下、向左走为负.如从点
A 到点 B 记为: A → B (+1,+4),从点 B 到点 A 记为: B → A
(-1,-4),括号内第一个数表示左右方向,第二个数表示
上下方向.解答下列问题:
(1) A → C ( , );
B → C ( , );
+3
+4
+2
0
(1)【解析】 A → C (+3,+4), B → C (+2,0).
故答案为+3,+4,+2,0.
(3)若这只甲虫从点 A 处去点 P 处的行走路线依次为(+2,
+2),(+2,-1),(-2,+3),(-1,-2),请在
图中标出点 P 的位置.
(3)解:点 P 如图所示.
1.下列各数:9,-3,-,0,+,+1,-2.3,0.2.其中正数有( )
A.5个 B.4个
C.3个 D.2个
B
2.在下列选项中,具有相反意义的量是( )
A.向东行30 m和向北行30 m
B.2个老师和2个学生
C.走了100 m和跑了100 m
D.收入20元和支出30元
D
3.下列说法错误的是( )
A.正分数一定是有理数
B.整数和分数统称为有理数
C.整数包括正整数、0和负整数
D.正数和负数统称为有理数
. .
D
4.在-3.5,,0.161 161 116…中,有理数有( )
A.1个 B.2个
C.3个 D.4个
B
5.下列说法中正确的是( )
A.没有最小的有理数
B.0既是正数也是负数
C.整数只包括正整数和负整数
D.-1是最大的负有理数
A
第二章 有理数及其运算 2.2
认识有理数
第1课时 有理数
1.由实例引出具有相反意义的量,并会表示具有相反意思的量。
2.进一步认识正数和负数,会判断一个数是正数还是负数.
3.理解有理数的意义,能按一定的标准对有理数进行分类.
学习目标
重点
重点
答对加10分
答错扣10分
不答得0分
第1题 第2题 第3题 第4题 第5题
第一队
第二队
第三队
第四队
用正、负数表示具有相反意义的量
知识点1
红色所表示的得
分比0分低
带“-”的得分比0分低
这里出现了比0分低的得分,我们可以用带有“-”号的数来表示,如-10(读作:负10)表示比0低10的数;
对于比0分高的得分,可以在前面加上“+”号,如+10(读作:正10)表示比0高10的数.
试一试:用带有“+”号和“-”号的数表示各队每道题的得分情况.试完成下表:
第1题 第2题 第3题 第4题 第5题
第一组
第二组
第三组
第四组
+10
-10
+10
+10
-10
-10
+10
0
+10
+10
+10
+10
-10
-10
0
+10
-10
+10
-10
-10
加10分表示+10分
扣10分表示-10分
得0分表示0分
像10,1.2,17…这样的数叫作正数,它们都比0大.
在正数前面加上“-”号的数叫作负数,例如-10,-3 …
你认为0应该放在什么地方?
0既不是正数,也不是负数
【归纳总结】
新知初探
贰
探究二 有理数的分类
思考:我们学过了哪些数?请举出相应的例子。
…… 负分数
1,2,3
0
-1,-2,-3
……正整数
……零
……负整数
…… 正分数
新知初探
贰
有理数的分类:
有理数
整数
分数
负分数
正分数
负整数
正整数
0
注意:小数≠分数
如1,2,3,…
0
如-1,-2,-3,…
如0.2, …
如 …
新知初探
贰
想一想:有理数还可以进行其他分类吗?
正有理数
负有理数
正分数
负分数
负整数
正整数
0
有理数
新知初探
贰
正数集合{ …};
负数集合{ …};
整数集合{ …};
正分数集合{ …};
负分数集合{ …};
分数集合{ …}.
巩固练习:把下面各数填在相应的括号里:
新知初探
贰
4.分数包括有限小数和无限循环小数。
小结
有理数的分类中的四点注意:
1.相对性:正数是相对负数而言的,整数是相对分数而言的。
2.特殊0:0既不是正数,也不是负数,但0是整数。
3.多属性:同一个数,可能属于多个不同的集合。如5既是正
数又是整数。
典例分析
例1:(1)转动转盘时,若规定顺时针转动为正,则逆时针转动5圈表示为________.
(2)若把后退规定为负,则+102米表示___________,0米表示__________.
(3)如果正午12时记作0时,午后3时记作+3时,那么上午8时记作________.
-5圈
前进102米
原地不动
-4时
例2:把下列各数填入相应的集合中:
典例分析
学以致用
1.如果收入100元记作+100元,那么支出100元记作( )
A.-100元 B.+100元 C.-200元 D.+200元
A
2.如果汽车向东行驶30米记作+30米,那么-50米表示( )
A.向东行驶50米 B.向西行驶50米 C.向南行驶50米 D.向北行驶50
3.在一次数学测试中,七(2) 班的平均分为 85 分,把高于平均分的高出部分数记为正数,老师将某一小组的美美、多多、田田、乐乐四位同学的成绩记为+7,-4,-11,+13,则这四位同学实际成绩最高的是 ( )
A.美美 B.多多 C.田田 D.乐乐
B
D
学以致用
4.下列说法中,正确的是( )
A.正整数和负整数统称整数
B.整数和分数统称有理数
C.零既可以是正整数,也可以是负整数
D.一个有理数不是正数就是负数
B
5.某食品包装袋上标有“净含量(385±5)克”,这包食品合格的净含量范围是____________.
380~390克
学以致用
-23,28,0,4
28,0,4
【变式训练】
1.(2024·东莞一模)如果温度上升10 ℃记作+10 ℃,那么温度下降7 ℃记作( )
A.+3 ℃ B.-3 ℃ C.+7 ℃ D.-7 ℃
【解析】如果温度上升10 ℃记作+10 ℃,那么温度下降7 ℃记作-7 ℃.
2.某种零件的直径合格尺寸为(5±0.1)mm,则下列零件直径合格的是( )
A.4.85 mm B.4.95 mm
C.5.11 mm D.5.15 mm
D
B
【重点2】有理数的分类(推理能力)
【典例2】(教材再开发·P25T2强化)请把下列各数填入相应的集合中:
-,-3,2,0,13.14,,10%.
负数集合{ …};
分数集合{ …}.
【自主解答】根据负数、分数的定义可得:
负数集合{-,-3,…};
分数集合{-,13.14,,10%,…}.
答案:-,-3 -,13.14,,10%
【变式训练】
1.(2024·湛江廉江一模)下列四个数中,负整数是( )
A.2 024 B.-3.14
C.0 D.-3
【解析】在2 024,-3.14,0,-3中,2 024是正整数,-3.14是负分数,0是整数,-3是负整数.
D
2.把下面各数填入图中相应的位置,并填写公共部分的名称.
-0.7,-10,+3.4,-109,-4,0,85,0.4.
【解析】根据有理数的分类法则得:
8.[2024天津和平区月考]据史料记载,早在两千多年前,中
国就有了正负数的概念,关于负数有下列4种说法:
①在某个数的前面加上符号“-”得到的数;
②不大于0的数;
③除去正数的其他数;
④在正数的前面加上符号“-”得到的数.
其中正确的是 (填序号).
④
分层练习-基础
分层练习-基础
知识点3 有理数的概念及其分类
9. 、 、 统称为整数,
与 统称为分数, 与 统称
为有理数.
正整数
零
负整数
正分数
负分数
整数
分数
10. 在π, ,-3, 这四个数中,整数是( C )
A. π B.
C. -3 D.
C
分层练习-基础
11.下列关于0的说法错误的是( A )
A. 任何情况下,0的实际意义就是什么都没有
B. 0是偶数不是奇数
C. 0既不是正数也不是负数
D. 0是整数也是有理数
A
12.把下列各数填入相应的集
合中:- ,0.618,-3.14,26,-2, ,0,
70%,-π.
正分数集合:{0.618, ,70%,…};
整数集合:{26,-2,0,…};
非负数集合:{0.618,26, ,0,70%,…};
负有理数集合:{- ,-3.14,-2,…}.
0.618, ,70%,
26,-2,0,
0.618,26, ,0,70%,
- ,-3.14,-2,
分层练习-基础
13.[2024南昌高新区月考]对于有理数:- ,1,8.6,-
7,0, ,-4 ,+101,-0.05,-9,下列说法正确
的是( D )
D
A. 只有1,-7,+101,-9是整数
B. 其中有三个数是正整数
C. 非负数有1,8.6,0,+101
D. 只有- ,-4 ,-0.05是负分数
分层练习-巩固
分层练习-巩固
14.规定45分钟为1个单位时间,并以每天上午9时记为0,9时以前的时间记为负数,9时以后的时间记为正数,例如:8:15记为-1;9:45记为+1,依此类推,则上午7:30应记为 .
-2
9. 某数学俱乐部有一种“秘密”的记账方式,当他们收入500
元时,记为-440元;当他们用去50元时,记为+110元.猜一
猜,当他们用去70元时,应记为 元.
【解析】500-440=60(元),110-50=60(元).
当他们用去70元时,应记为70+60=130(元).
故答案为+130.
+130
13. (选做)如图,一只甲虫在5×5的网格(每小格边长为1)
上沿着网格线运动.它从点 A 处出发去看望点 B , C , D 处的其
他甲虫.规定:向上、向右走为正,向下、向左走为负.如从点
A 到点 B 记为: A → B (+1,+4),从点 B 到点 A 记为: B → A
(-1,-4),括号内第一个数表示左右方向,第二个数表示
上下方向.解答下列问题:
(1) A → C ( , );
B → C ( , );
+3
+4
+2
0
(1)【解析】 A → C (+3,+4), B → C (+2,0).
故答案为+3,+4,+2,0.
(3)若这只甲虫从点 A 处去点 P 处的行走路线依次为(+2,
+2),(+2,-1),(-2,+3),(-1,-2),请在
图中标出点 P 的位置.
(3)解:点 P 如图所示.
1.下列各数:9,-3,-,0,+,+1,-2.3,0.2.其中正数有( )
A.5个 B.4个
C.3个 D.2个
B
2.在下列选项中,具有相反意义的量是( )
A.向东行30 m和向北行30 m
B.2个老师和2个学生
C.走了100 m和跑了100 m
D.收入20元和支出30元
D
3.下列说法错误的是( )
A.正分数一定是有理数
B.整数和分数统称为有理数
C.整数包括正整数、0和负整数
D.正数和负数统称为有理数
. .
D
4.在-3.5,,0.161 161 116…中,有理数有( )
A.1个 B.2个
C.3个 D.4个
B
5.下列说法中正确的是( )
A.没有最小的有理数
B.0既是正数也是负数
C.整数只包括正整数和负整数
D.-1是最大的负有理数
A
同课章节目录
