2.2认识有理数第1课时- 有理数 课件(共39张PPT)
文档属性
| 名称 | 2.2认识有理数第1课时- 有理数 课件(共39张PPT) |  | |
| 格式 | pptx | ||
| 文件大小 | 10.3MB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 鲁教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2025-05-30 18:07:06 | ||
图片预览








文档简介
(共39张PPT)
第1课时 有理数
第二章 有理数及其运算
1 认识有理数
课标要求 核心素养
1.理解负数的意义,会用正数和负数表示具体情境中具有相反意义的量;理解有理数的意义,能用数轴上的点表示有理数。 2.能借助数轴体会相反数和绝对值的意义,初步体会数形结合的思想方法。 3.能比较有理数的大小;能求有理数的相反数和绝对值。 4.理解乘方的意义,会运用乘方的意义准确进行有理数的乘方运算。 5.能熟练地对有理数进行加、减、乘、除、乘方及简单的混合运算(以三步以内为主),理解有理数的运算律,能合理运用运算律简化运算。 6.能运用有理数的运算解决简单问题。 运算能力
推理能力
创新意识
应用意识
情境导入
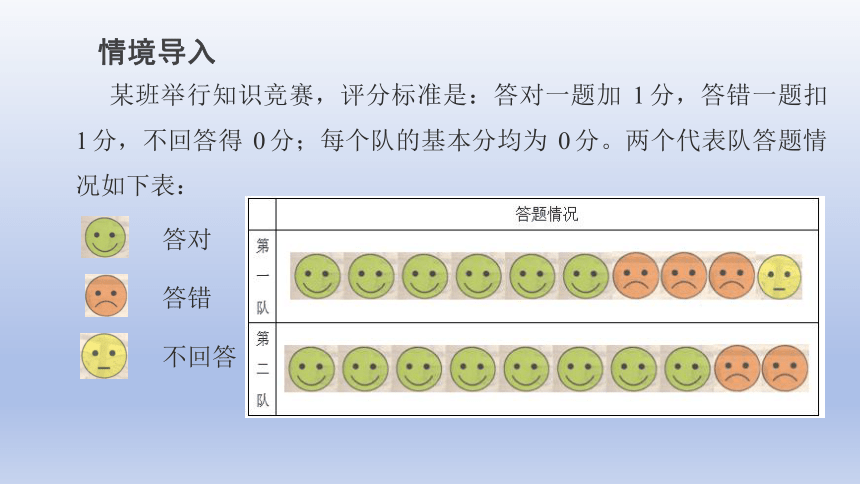
某班举行知识竞赛,评分标准是:答对一题加 1 分,答错一题扣 1 分,不回答得 0 分;每个队的基本分均为 0 分。两个代表队答题情况如下表:
答对
答错
不回答
情境导入
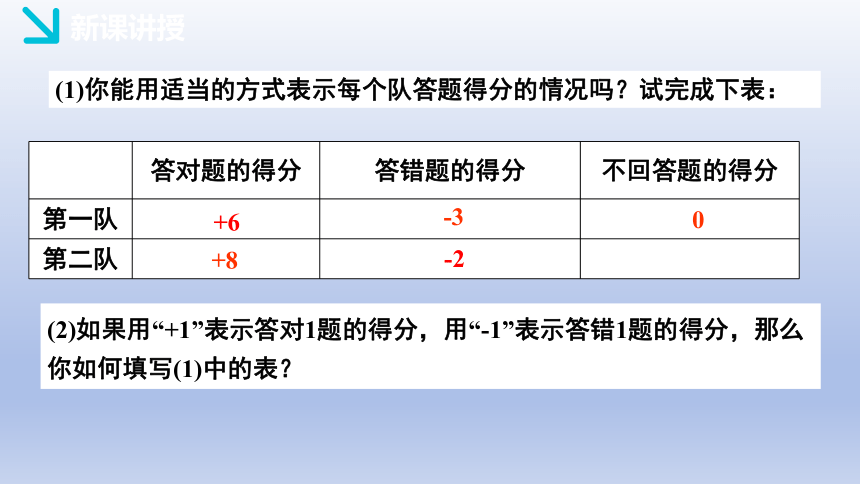
(1)你能用适当的方式表示每个队答题得分的情况吗?试完成下表:
答对题的得分 答错题的得分 未回答题的得分
第一队 +6
第二队 -2
(2)如果用“+1”表示答对题所得的分,用“-1”表示答错一题得分,那么你如何填写(1)中的表?
新知初探
贰
新课讲授
探究一:认识负数
某班举行知识竞赛,评分标准是:答对一题加1分,答错一题扣1分,不回答得0分;每个队的基本分均为0分.下表是用下图所示的表情表示的两个参赛队的答题情况.:
新课讲授
答对题的得分 答错题的得分 不回答题的得分
第一队
第二队
-3
0
+8
(1)你能用适当的方式表示每个队答题得分的情况吗?试完成下表:
(2)如果用“+1”表示答对1题的得分,用“-1”表示答错1题的得分,那么你如何填写(1)中的表?
+6
-2
吐鲁番盆地
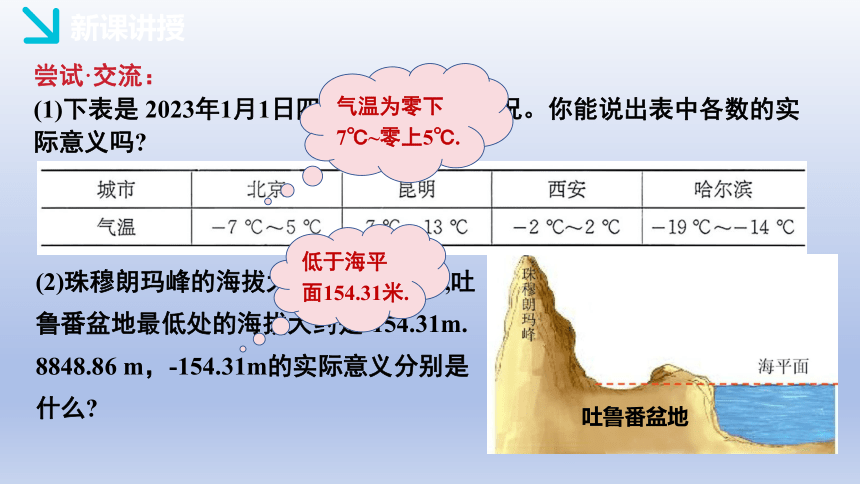
(2)珠穆朗玛峰的海拔大约是8848.86m,吐鲁番盆地最低处的海拔大约是-154.31m.
8848.86 m,-154.31m的实际意义分别是什么
新课讲授
尝试·交流:
(1)下表是 2023年1月1日四个城市的气温情况。你能说出表中各数的实际意义吗
气温为零下7℃~零上5℃.
低于海平面154.31米.
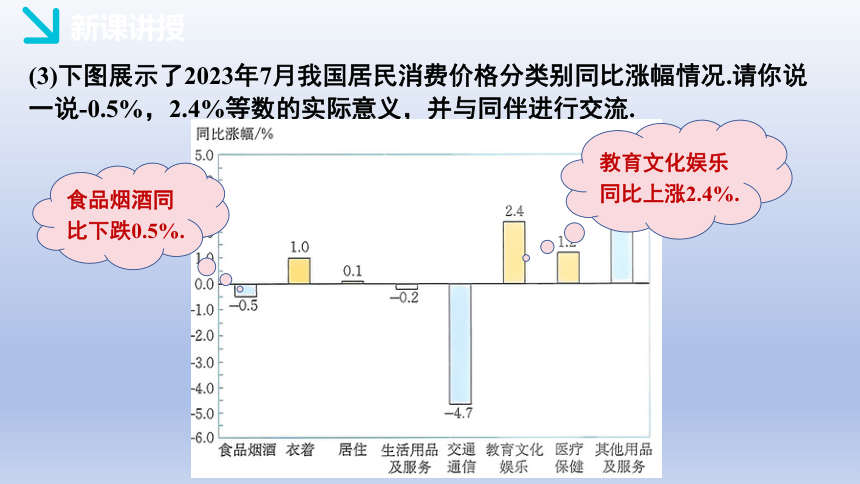
(3)下图展示了2023年7月我国居民消费价格分类别同比涨幅情况.请你说一说-0.5%,2.4%等数的实际意义,并与同伴进行交流.
新课讲授
食品烟酒同比下跌0.5%.
教育文化娱乐同比上涨2.4%.
新课讲授
“加分与扣分”““零上温度与零下温度”“高于海平面与低于海平面”
“上涨量与下跌量”等都是具有相反意义的量。
为了表示具有相反意义的量,我们可以把其中一个量规定为正的,把与这个量意义相反的量规定为负的,并分别用“+”“_”来表示。例如,“加3分”记为+3分,“扣2分”就记为-2分。
新课讲授
正数和负数的概念
知识归纳
1.像+3,+15,+2.4%,...都是正数,正数前面的“+”可以省略不写.
2.像-2,-8,-0.5%,…都是负数.
3.0既不是正数,也不是负数.
注意:负数与对应的正数在数量上相等,表示的意义相反.
你能将所学的数进行分类吗?与同伴进行交流。
新知探究
2.有理数的分类
我们以前学过的数,
像1,2,3,…称为正整数;
,…称为正分数.
形如-1,-2,-3,…称为负整数;
,…称为负分数.
那么小数和0呢?我们该怎么分类将它们包含进去?
概念归纳
正整数、零和负整数统称整数.
整数和分数统称有理数.
正分数和负分数统称分数.
目前我们所学的小数都可以化成分数,所以把小数划分到分数一类.
概念归纳
1.有理数的分类
(1)按有理数的定义分类 (2) 按性质分类
有理数
正整数
负整数
负分数
正有理数
负有理数
正分数
零
正整数
负整数
零
正分数
负分数
整数
分数
有理数
随堂练习
1.(1)如果零上 5℃ 记作 +5℃,那么零下 3℃ 记作什么?
(2)东、西为两个相反方向,如果-4m表示一个物体向西运动 4m,那么+2m表示什么?物体原地不动记作什么?
(3)某仓库运进面粉 7.5t 记作+7.5t,那么运出面粉 3.8t 记作什么?
解:(1)零下3℃记作﹣3℃.
解:(2)﹢2m表示物体向东运动2m,物体原地不动记作0m.
解:(3)运出面粉 3.8 t 应记作﹣3.8 t.
2.所有的正数组成正数集合,所有的负数组成负数集合,所有的整数组成整数集合,所有的分数组成分数集合。请把下列各数填入相应的集合中:
3,-7,,,0,-8,15,。
正数集合:{ }
负数集合:{ }
整数集合:{ }
分数集合:{ }
随堂练习
正数和负数在实际生活中的应用
例 体育课上,全班女生进行了百米跑步测验,把跑步时间达标成绩18秒记为0,大于18秒的用正数表示,小于18秒的用负数表示.第一小组8名女生的百米跑步成绩如下:
-3,+0.9,0,-2.6,-0.3,+1.1,+1.6,-0.1.
问第一小组女生的达标率为多少 达标率=×100%
解:第一小组女生达标的有-3,0,-2.6,-0.3,-0.1,共计5人.
达标率=×100%=×100%=62.5%.
答:第一小组女生的达标率为62.5%.
变式训练
某公司共有5名销售人员,他们本月的销售额(单位:万元)分别为5,4.8,7.6,3.6,4.为了让经理方便地看出每位员工与本月人均销售额的差距,你能用正负数表示他们的销售额吗
解:本月人均销售额为(5+4.8+7.6+3.6+4)÷5=5万元,所以用正负数表示他们每个人的销售额为0,-0.2,2.6,-1.4,-1.
1.下列说法中正确的是 ( )
A.正整数、负整数统称为整数
B.正分数和负分数统称为分数
C.零既可以是正整数,也可以是负整数
D.一个有理数不是正数就是负数
B
数学 七年级上册 BS版
典例讲练
0 2
(1)如果收入50元记作+50元,那么支出40元记作
元.
-40
【思路导航】(1)收入与支出是具有相反意义的量,收入记为正,则支出记为负;
【解析】(1)根据题意,收入50元记作+50元,则支出40元记
作-40元.故答案为-40.
(2)下列各组量中,具有相反意义的量有 (填序号).
①胜2局与负3局;②水温上升30℃与气温下降20℃;③向东走
2m与向南走5m;④增产与减产.
【思路导航】(2)相反意义的量与表达含义有关与数字大小无关.
①
【解析】(2)①胜2局与负3局是一组具有相反意义的量,故①符合题意;②水温上升30℃与气温下降20℃不是一组具有相反意义的量,故②不符合题意;③向东走2m与向南走5m不是一组具有相反意义的量,故③不符合题意;④增产与减产是反义词,但没有说明是哪两个量,故④不符合题意.综上所述,具有相反意义是①.故答案为①.
【点拨】口诀:相反意义成双对,还要数量和单位,你为正来
我为负,正负兄弟齐上阵.
1. 在一次数学测试中,95分及以上成绩为优秀,故以95分为标
准,如106分记为+11分,则86分应记为 分.
2. 某公司生产的一种小零食的包装袋上印有(70±2)g的字
样.质检局随机抽查了5袋该产品,质量分别为67g、69g、70g、
71g、74g,其中合格的共有 袋.
-9
3
当堂小结
负整数
0
正分数
正整数
整数
分数
负分数
有理数
0
正有理数
负有理数
有理数
正整数
负整数
正分数
负分数
定义分类
符号分类
课堂练习
1. 下列说法,正确的是 ( )
A. 加正号的数是正数,加负号的数是负数
B. 0 是最小的正数
C. 字母 a 既可为正数,也可为负数,还可为 0
D. 任意一个数,不是正数就是负数
C
2.把下列各数填入相应的集合内:
,-3.1416,0,2022, ,-0.23456,10%,10.1,0.67,-89
…
…
正数集合
负数集合
…
…
整数集合
分数集合
2022
10.1
0.67
-3.1416
-0.23456
-89
10%
0
2022
-89
-3.1416
-0.23456
10%
10.1
0.67
3.某老师要测量全班学生的身高,他以 1.60 米为基准,将某一小组 5 名学生的身高 (单位:米) 简记为:
﹢0.12,﹣0.05,0,﹢0.07,﹣0.02。这里的正数、负数分别表示什么意义?这 5 名学生的实际身高分别为多少?
负数表示学生身高低于 1.60 米。
1.60+0.12=1.72 (米),
1.60﹣0.05=1.55 (米),
1.60+0.07=1.67 (米),
1.60﹣0.02=1.58 (米)。
答:实际身高分别 1.72、1.55、1.60、1.67、1.58 米。
解:正数表示学生身高超过 1.60 米;
3.(2024·汕头龙湖一模)某种速冻水饺的储藏温度是(-18±2)℃,下列四个冷藏室的温
度中,不适合储藏此种水饺的是( )
A.-24 ℃ B.-18 ℃ C.-17 ℃ D.-16 ℃
【解析】因为速冻水饺的储藏温度是-18±2 ℃,
所以速冻水饺的储藏温度是-20~-16 ℃,选项A符合题意.
4.(2024·汕尾陆丰期末)大自然的鬼斧神工孕育了我国恢宏壮阔的地形,珠穆朗玛峰
约在海平面上8 848.86 m,记为+8 848.86 m,吐鲁番盆地的艾丁湖约在海平面下154.31 m,
记为_____________.
【解析】珠穆朗玛峰约在海平面上8 848.86 m,记为+8 848.86 m,吐鲁番盆地的艾丁
湖约在海平面下154.31 m,记为-154.31 m.
A
-154.31 m
【能力练】
5.(2024·深圳龙岗模拟)某运动项目的比赛规定,胜一场记作“+1”分,平局记作“0”分,如果某队得到“-1”分,则该队在比赛中( )
A.与对手打成平局 B.输给了对手
C.打赢了对手 D.无法确定
【解析】某运动项目的比赛规定,胜一场记作“+1”分,平局记作“0”分,如果某队得到
“-1”分,则该队在比赛中输给了对手.
B
6.(2024·广州南沙期末)一袋大米的包装袋上标注的质量是(30±0.2)kg,由此可知符合
标准的一袋大米的质量应最少不能低于________kg.
【解析】30±0.2的含义为比30多0.2或比30少0.2,所以符合标注质量的一袋大米的质
量在(30-0.2)kg至(30+0.2)kg之间,所以符合标注质量的一袋大米的质量在29.8 kg至
30.2 kg之间,由此可知符合标准的一袋大米的质量应最少不能低于29.8 kg.
7.(2024·惠州博罗期末)在有理数0,6,-5,-,9中,整数有___________;负数有__________.
【解析】整数有0,6,-5,9;
负数有-5,-.
29.8
0,6,-5,9
-5,-
【培优练】
8.(抽象能力、推理能力)已知A,B,C三个“数的家族”:
A:{-1,3.1,-4,6,2.1};
B:{-4.2,2.1,-1,10,-};
C:{2.1,-4.2,8,6}.
(1)请把每个“数的家族”中所含的数填入图中的相应部分.
(2)把A,B,C三个“数的家族”中的负数写在横线上: .
(3)有没有同时属于A,B,C三个“数的家族”的数 若有,请指出.
【解析】(1)如图所示.
(2)答案:-1,-4,-4.2,-
(3)有,三个“数的家族”的共有数是2.1.
数学 九年级上册 BS版
C级 拓展训练
0 3
13. (选做)如图,一只甲虫在5×5的网格(每小格边长为1)
上沿着网格线运动.它从点 A 处出发去看望点 B , C , D 处的其
他甲虫.规定:向上、向右走为正,向下、向左走为负.如从点
A 到点 B 记为: A → B (+1,+4),从点 B 到点 A 记为: B → A
(-1,-4),括号内第一个数表示左右方向,第二个数表示
上下方向.解答下列问题:
(1) A → C ( , );
B → C ( , );
+3
+4
+2
0
(1)【解析】 A → C (+3,+4), B → C (+2,0).
故答案为+3,+4,+2,0.
(2)若这只甲虫的行走路线为 A → B → C → D ,请计算该甲虫
走过的路程;
(2)解:1+4+2+1+2=10.
故该甲虫走过的路程为10.
(3)若这只甲虫从点 A 处去点 P 处的行走路线依次为(+2,
+2),(+2,-1),(-2,+3),(-1,-2),请在
图中标出点 P 的位置.
(3)解:点 P 如图所示.
演示完毕 谢谢观看
第1课时 有理数
第二章 有理数及其运算
1 认识有理数
课标要求 核心素养
1.理解负数的意义,会用正数和负数表示具体情境中具有相反意义的量;理解有理数的意义,能用数轴上的点表示有理数。 2.能借助数轴体会相反数和绝对值的意义,初步体会数形结合的思想方法。 3.能比较有理数的大小;能求有理数的相反数和绝对值。 4.理解乘方的意义,会运用乘方的意义准确进行有理数的乘方运算。 5.能熟练地对有理数进行加、减、乘、除、乘方及简单的混合运算(以三步以内为主),理解有理数的运算律,能合理运用运算律简化运算。 6.能运用有理数的运算解决简单问题。 运算能力
推理能力
创新意识
应用意识
情境导入
某班举行知识竞赛,评分标准是:答对一题加 1 分,答错一题扣 1 分,不回答得 0 分;每个队的基本分均为 0 分。两个代表队答题情况如下表:
答对
答错
不回答
情境导入
(1)你能用适当的方式表示每个队答题得分的情况吗?试完成下表:
答对题的得分 答错题的得分 未回答题的得分
第一队 +6
第二队 -2
(2)如果用“+1”表示答对题所得的分,用“-1”表示答错一题得分,那么你如何填写(1)中的表?
新知初探
贰
新课讲授
探究一:认识负数
某班举行知识竞赛,评分标准是:答对一题加1分,答错一题扣1分,不回答得0分;每个队的基本分均为0分.下表是用下图所示的表情表示的两个参赛队的答题情况.:
新课讲授
答对题的得分 答错题的得分 不回答题的得分
第一队
第二队
-3
0
+8
(1)你能用适当的方式表示每个队答题得分的情况吗?试完成下表:
(2)如果用“+1”表示答对1题的得分,用“-1”表示答错1题的得分,那么你如何填写(1)中的表?
+6
-2
吐鲁番盆地
(2)珠穆朗玛峰的海拔大约是8848.86m,吐鲁番盆地最低处的海拔大约是-154.31m.
8848.86 m,-154.31m的实际意义分别是什么
新课讲授
尝试·交流:
(1)下表是 2023年1月1日四个城市的气温情况。你能说出表中各数的实际意义吗
气温为零下7℃~零上5℃.
低于海平面154.31米.
(3)下图展示了2023年7月我国居民消费价格分类别同比涨幅情况.请你说一说-0.5%,2.4%等数的实际意义,并与同伴进行交流.
新课讲授
食品烟酒同比下跌0.5%.
教育文化娱乐同比上涨2.4%.
新课讲授
“加分与扣分”““零上温度与零下温度”“高于海平面与低于海平面”
“上涨量与下跌量”等都是具有相反意义的量。
为了表示具有相反意义的量,我们可以把其中一个量规定为正的,把与这个量意义相反的量规定为负的,并分别用“+”“_”来表示。例如,“加3分”记为+3分,“扣2分”就记为-2分。
新课讲授
正数和负数的概念
知识归纳
1.像+3,+15,+2.4%,...都是正数,正数前面的“+”可以省略不写.
2.像-2,-8,-0.5%,…都是负数.
3.0既不是正数,也不是负数.
注意:负数与对应的正数在数量上相等,表示的意义相反.
你能将所学的数进行分类吗?与同伴进行交流。
新知探究
2.有理数的分类
我们以前学过的数,
像1,2,3,…称为正整数;
,…称为正分数.
形如-1,-2,-3,…称为负整数;
,…称为负分数.
那么小数和0呢?我们该怎么分类将它们包含进去?
概念归纳
正整数、零和负整数统称整数.
整数和分数统称有理数.
正分数和负分数统称分数.
目前我们所学的小数都可以化成分数,所以把小数划分到分数一类.
概念归纳
1.有理数的分类
(1)按有理数的定义分类 (2) 按性质分类
有理数
正整数
负整数
负分数
正有理数
负有理数
正分数
零
正整数
负整数
零
正分数
负分数
整数
分数
有理数
随堂练习
1.(1)如果零上 5℃ 记作 +5℃,那么零下 3℃ 记作什么?
(2)东、西为两个相反方向,如果-4m表示一个物体向西运动 4m,那么+2m表示什么?物体原地不动记作什么?
(3)某仓库运进面粉 7.5t 记作+7.5t,那么运出面粉 3.8t 记作什么?
解:(1)零下3℃记作﹣3℃.
解:(2)﹢2m表示物体向东运动2m,物体原地不动记作0m.
解:(3)运出面粉 3.8 t 应记作﹣3.8 t.
2.所有的正数组成正数集合,所有的负数组成负数集合,所有的整数组成整数集合,所有的分数组成分数集合。请把下列各数填入相应的集合中:
3,-7,,,0,-8,15,。
正数集合:{ }
负数集合:{ }
整数集合:{ }
分数集合:{ }
随堂练习
正数和负数在实际生活中的应用
例 体育课上,全班女生进行了百米跑步测验,把跑步时间达标成绩18秒记为0,大于18秒的用正数表示,小于18秒的用负数表示.第一小组8名女生的百米跑步成绩如下:
-3,+0.9,0,-2.6,-0.3,+1.1,+1.6,-0.1.
问第一小组女生的达标率为多少 达标率=×100%
解:第一小组女生达标的有-3,0,-2.6,-0.3,-0.1,共计5人.
达标率=×100%=×100%=62.5%.
答:第一小组女生的达标率为62.5%.
变式训练
某公司共有5名销售人员,他们本月的销售额(单位:万元)分别为5,4.8,7.6,3.6,4.为了让经理方便地看出每位员工与本月人均销售额的差距,你能用正负数表示他们的销售额吗
解:本月人均销售额为(5+4.8+7.6+3.6+4)÷5=5万元,所以用正负数表示他们每个人的销售额为0,-0.2,2.6,-1.4,-1.
1.下列说法中正确的是 ( )
A.正整数、负整数统称为整数
B.正分数和负分数统称为分数
C.零既可以是正整数,也可以是负整数
D.一个有理数不是正数就是负数
B
数学 七年级上册 BS版
典例讲练
0 2
(1)如果收入50元记作+50元,那么支出40元记作
元.
-40
【思路导航】(1)收入与支出是具有相反意义的量,收入记为正,则支出记为负;
【解析】(1)根据题意,收入50元记作+50元,则支出40元记
作-40元.故答案为-40.
(2)下列各组量中,具有相反意义的量有 (填序号).
①胜2局与负3局;②水温上升30℃与气温下降20℃;③向东走
2m与向南走5m;④增产与减产.
【思路导航】(2)相反意义的量与表达含义有关与数字大小无关.
①
【解析】(2)①胜2局与负3局是一组具有相反意义的量,故①符合题意;②水温上升30℃与气温下降20℃不是一组具有相反意义的量,故②不符合题意;③向东走2m与向南走5m不是一组具有相反意义的量,故③不符合题意;④增产与减产是反义词,但没有说明是哪两个量,故④不符合题意.综上所述,具有相反意义是①.故答案为①.
【点拨】口诀:相反意义成双对,还要数量和单位,你为正来
我为负,正负兄弟齐上阵.
1. 在一次数学测试中,95分及以上成绩为优秀,故以95分为标
准,如106分记为+11分,则86分应记为 分.
2. 某公司生产的一种小零食的包装袋上印有(70±2)g的字
样.质检局随机抽查了5袋该产品,质量分别为67g、69g、70g、
71g、74g,其中合格的共有 袋.
-9
3
当堂小结
负整数
0
正分数
正整数
整数
分数
负分数
有理数
0
正有理数
负有理数
有理数
正整数
负整数
正分数
负分数
定义分类
符号分类
课堂练习
1. 下列说法,正确的是 ( )
A. 加正号的数是正数,加负号的数是负数
B. 0 是最小的正数
C. 字母 a 既可为正数,也可为负数,还可为 0
D. 任意一个数,不是正数就是负数
C
2.把下列各数填入相应的集合内:
,-3.1416,0,2022, ,-0.23456,10%,10.1,0.67,-89
…
…
正数集合
负数集合
…
…
整数集合
分数集合
2022
10.1
0.67
-3.1416
-0.23456
-89
10%
0
2022
-89
-3.1416
-0.23456
10%
10.1
0.67
3.某老师要测量全班学生的身高,他以 1.60 米为基准,将某一小组 5 名学生的身高 (单位:米) 简记为:
﹢0.12,﹣0.05,0,﹢0.07,﹣0.02。这里的正数、负数分别表示什么意义?这 5 名学生的实际身高分别为多少?
负数表示学生身高低于 1.60 米。
1.60+0.12=1.72 (米),
1.60﹣0.05=1.55 (米),
1.60+0.07=1.67 (米),
1.60﹣0.02=1.58 (米)。
答:实际身高分别 1.72、1.55、1.60、1.67、1.58 米。
解:正数表示学生身高超过 1.60 米;
3.(2024·汕头龙湖一模)某种速冻水饺的储藏温度是(-18±2)℃,下列四个冷藏室的温
度中,不适合储藏此种水饺的是( )
A.-24 ℃ B.-18 ℃ C.-17 ℃ D.-16 ℃
【解析】因为速冻水饺的储藏温度是-18±2 ℃,
所以速冻水饺的储藏温度是-20~-16 ℃,选项A符合题意.
4.(2024·汕尾陆丰期末)大自然的鬼斧神工孕育了我国恢宏壮阔的地形,珠穆朗玛峰
约在海平面上8 848.86 m,记为+8 848.86 m,吐鲁番盆地的艾丁湖约在海平面下154.31 m,
记为_____________.
【解析】珠穆朗玛峰约在海平面上8 848.86 m,记为+8 848.86 m,吐鲁番盆地的艾丁
湖约在海平面下154.31 m,记为-154.31 m.
A
-154.31 m
【能力练】
5.(2024·深圳龙岗模拟)某运动项目的比赛规定,胜一场记作“+1”分,平局记作“0”分,如果某队得到“-1”分,则该队在比赛中( )
A.与对手打成平局 B.输给了对手
C.打赢了对手 D.无法确定
【解析】某运动项目的比赛规定,胜一场记作“+1”分,平局记作“0”分,如果某队得到
“-1”分,则该队在比赛中输给了对手.
B
6.(2024·广州南沙期末)一袋大米的包装袋上标注的质量是(30±0.2)kg,由此可知符合
标准的一袋大米的质量应最少不能低于________kg.
【解析】30±0.2的含义为比30多0.2或比30少0.2,所以符合标注质量的一袋大米的质
量在(30-0.2)kg至(30+0.2)kg之间,所以符合标注质量的一袋大米的质量在29.8 kg至
30.2 kg之间,由此可知符合标准的一袋大米的质量应最少不能低于29.8 kg.
7.(2024·惠州博罗期末)在有理数0,6,-5,-,9中,整数有___________;负数有__________.
【解析】整数有0,6,-5,9;
负数有-5,-.
29.8
0,6,-5,9
-5,-
【培优练】
8.(抽象能力、推理能力)已知A,B,C三个“数的家族”:
A:{-1,3.1,-4,6,2.1};
B:{-4.2,2.1,-1,10,-};
C:{2.1,-4.2,8,6}.
(1)请把每个“数的家族”中所含的数填入图中的相应部分.
(2)把A,B,C三个“数的家族”中的负数写在横线上: .
(3)有没有同时属于A,B,C三个“数的家族”的数 若有,请指出.
【解析】(1)如图所示.
(2)答案:-1,-4,-4.2,-
(3)有,三个“数的家族”的共有数是2.1.
数学 九年级上册 BS版
C级 拓展训练
0 3
13. (选做)如图,一只甲虫在5×5的网格(每小格边长为1)
上沿着网格线运动.它从点 A 处出发去看望点 B , C , D 处的其
他甲虫.规定:向上、向右走为正,向下、向左走为负.如从点
A 到点 B 记为: A → B (+1,+4),从点 B 到点 A 记为: B → A
(-1,-4),括号内第一个数表示左右方向,第二个数表示
上下方向.解答下列问题:
(1) A → C ( , );
B → C ( , );
+3
+4
+2
0
(1)【解析】 A → C (+3,+4), B → C (+2,0).
故答案为+3,+4,+2,0.
(2)若这只甲虫的行走路线为 A → B → C → D ,请计算该甲虫
走过的路程;
(2)解:1+4+2+1+2=10.
故该甲虫走过的路程为10.
(3)若这只甲虫从点 A 处去点 P 处的行走路线依次为(+2,
+2),(+2,-1),(-2,+3),(-1,-2),请在
图中标出点 P 的位置.
(3)解:点 P 如图所示.
演示完毕 谢谢观看
同课章节目录
