20.1.2 中位数和众数课件
图片预览






文档简介
(共19张PPT)
20.1 数据的集中趋势
第1课时 中位数和众数
20.1.2 中位数和众数
情景
导入
合作
探究
课堂
小结
随堂
训练
阿Q回忆十年前大学毕业后找工作经历,开始想找一份月薪在1700以上的工作,那天他看见三毛公司门口的招聘广告,上面写着:现因业务需要招员工一名,有意者欢迎前来应聘,当时阿Q走了进去……
阿Q应聘
情景导入
我们好几人工资都是1100元.
职
员
D
职员C
我的工资是1200元,在公司中算中等收入.
?
阿Q
我公司员工的收入很高,月平均工资为2000元.
经理
那时阿Q问了三毛公司的所有员工的月薪,列出如下统计表:
员工 经理 副经理 职员A 职员B 职员C 职员D 职员E 职员F 杂工G
月薪(元) 6000 4000 1700 1300 1200 1100 1100 1100 500
1.经理说平均工资有2000元对不对?
2.你觉得用平均数代表三毛公司的员工工资合适吗?
3.你认为阿Q如果在该公司应聘,工资能达到阿Q
预想的要求吗?他的工资很可能是哪个数?试说明
理由,与同伴交流.
三毛公司的工资水平到底怎样?我该不该去应聘?
合作探究
活动:探究中位数及众数的定义及确定方法
将9人的工资按由低到高的顺序排列,处在正中间位置是中位数.
500 1100 1100 1100 1200 1300 1700 4000 6000
什么是中位数?
它就是中位数
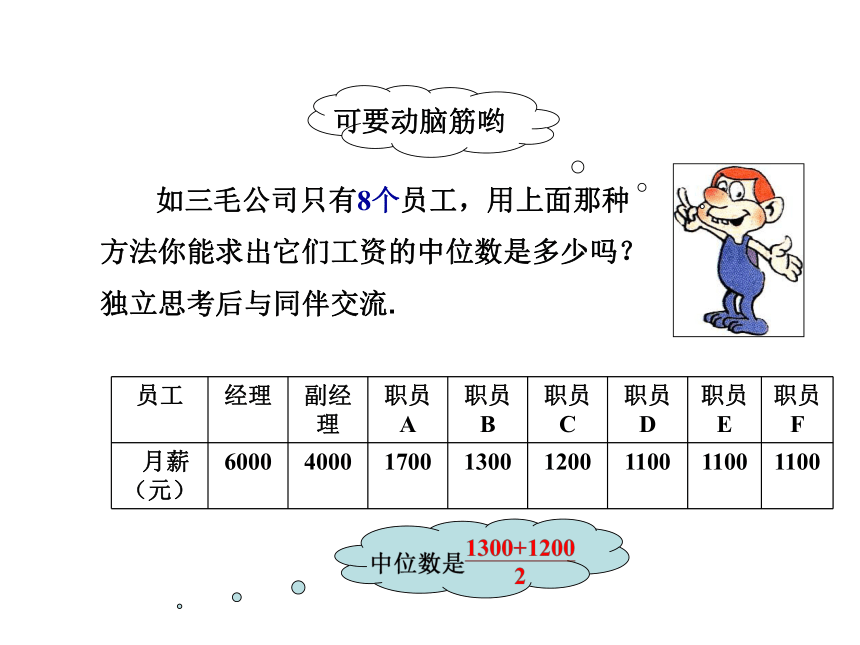
员工 经理 副经理 职员A 职员B 职员C 职员D 职员E 职员F
月薪 (元) 6000 4000 1700 1300 1200 1100 1100 1100
如三毛公司只有8个员工,用上面那种方法你能求出它们工资的中位数是多少吗?独立思考后与同伴交流.
可要动脑筋哟
该公司9员工的工资中出现的频数最多的那个工资,就是他们工资的众数,如:
什么是众数?
1700
6000
4000
1300
1200
1100
500
月薪 6000 4000 1700 1300 1200 1100 500
频数 1 1 1 1 1 3 1
它就是众数
1700
6000
4000
1300
1200
1100
500
月薪 6000 4000 1700 1300 1200 1100 500
频数 1 2 3 1 2 3 1
如果有两个工资的频数并列最多,那么这组数据的众数是什么?独立思考后小组交流.
它是众数
它是众数
如果每个工资数的频数都相同,那么这组数据的众数是什么?独立思考后小组交流.
月薪 6000 4000 1700 1300 1200 1100 500
频数 1 1 1 1 1 1 1
1700
6000
4000
1300
1200
1100
500
这种情况没有众数
工资太低了!找别家吧!
又看到一家电视台在招天气预报员,当时想着我去试试
阿Q又到一家电视台应聘天气预报员,电视台让他把当天(2010年6月9日)的天气预报说一遍,于是阿Q集中精力把我国各大城市的天气预报说了一遍,最后又补说了一句:我国34大城市当日的最高气温(0c)平均数为29度,中位数为30度,众数为31度,你认为阿Q说得对吗?
北京32 天津33 石家庄36 太原
31 呼和浩特27 沈阳
27 长春
26 哈尔滨26 上海
34
南京32 杭州32 合肥32 福州
36 南昌
30 济南
33 郑州
34 武汉
31 长沙
29
广州35 海口35 南宁36 成都
29 重庆
27 贵阳
24 昆明
23 拉萨
21 西安
33
兰州28 银川30 西宁26 乌鲁木齐29 台北
31 香港
36 澳门
35
阿Q说天气预报
他们说我说错了,我当时想回去要好好学习!
1.中位数是一个位置代表值,利用中位数分析数据可以获得一些信息。如果已知一组数据的中位数,那么可以知道,在这组数据中,有一半数比中位数大,有一半数比中位数小.即小于或大于这个中位数的数据各占一半.
2.求中位数的一般步骤:先排序、看奇偶,再确定中位数.
3.中间位置确定确定方法是:
n 为奇数时,中间位置是第 个
n为偶数时,中间位置是第 , 个的平均数
知识要点
如果所有数据出现的次数都一样,那么这组数据没有众数.例如:1,2,3,4,5没有众数.
一般来说,一组数据中,出现次数最多的数就叫这组数据的众数.例如:1,2,3,3,4的众数是3.
如果有两个或两个以上个数出现次数都是最多的,那么这几个数都是这组数据的众数.例如:1,2,2,3,3,4的众数是2和3.
例1 下面两组数据的中位数、众数分别是多少?
(1)5,6,2,3,2
(2)5,6,2,4,3,5
确定中位数要先排序、看奇偶,再确定中位数;确定众数找出现次数最多的数据.
解:(1) 中位数是3,众数是2;
(2)中位数是4.5,众数是5.
提示
例2.已知一组数据10,10,x,8(由大到小排列)的中位数与平均数相等,求x值及这组数据的中位数.
解:∵10,10,x,8的中位数与平均数相等
∴ (10+x)/2=(10+10+x+8)/4
∴x=8
(10+x)/2=9
∴这组数据中的中位数是9.
若没有“由大到小排列”,则情况又如何?
1.中位数、众数的定义及确定方法
中位数:将一组数据按照由小到大的顺序排列,如果数据的个数是奇数,则称处于中间位置的数为这组数据的中位数;如果数据的个数是偶数,则称中间两个数据的平均数为这组数据的中位数.
众数:一组数据中出现次数最多的数据称为这组数据的众数.
课堂小结
2.中位数、众数的意义及作用
中位数是位置代表值,小于或大于这个中位数的数据各占一半;众数往往是人们最为关心的一个量.
3.中位数、众数的区别
中位数是一组数据中唯一的,可能是这组数据中的数据,也可能不是这组数据中的数据;而一组数据中的众数可能不止一个,而且一定是这组数据中的数据.
20.1 数据的集中趋势
第1课时 中位数和众数
20.1.2 中位数和众数
情景
导入
合作
探究
课堂
小结
随堂
训练
阿Q回忆十年前大学毕业后找工作经历,开始想找一份月薪在1700以上的工作,那天他看见三毛公司门口的招聘广告,上面写着:现因业务需要招员工一名,有意者欢迎前来应聘,当时阿Q走了进去……
阿Q应聘
情景导入
我们好几人工资都是1100元.
职
员
D
职员C
我的工资是1200元,在公司中算中等收入.
?
阿Q
我公司员工的收入很高,月平均工资为2000元.
经理
那时阿Q问了三毛公司的所有员工的月薪,列出如下统计表:
员工 经理 副经理 职员A 职员B 职员C 职员D 职员E 职员F 杂工G
月薪(元) 6000 4000 1700 1300 1200 1100 1100 1100 500
1.经理说平均工资有2000元对不对?
2.你觉得用平均数代表三毛公司的员工工资合适吗?
3.你认为阿Q如果在该公司应聘,工资能达到阿Q
预想的要求吗?他的工资很可能是哪个数?试说明
理由,与同伴交流.
三毛公司的工资水平到底怎样?我该不该去应聘?
合作探究
活动:探究中位数及众数的定义及确定方法
将9人的工资按由低到高的顺序排列,处在正中间位置是中位数.
500 1100 1100 1100 1200 1300 1700 4000 6000
什么是中位数?
它就是中位数
员工 经理 副经理 职员A 职员B 职员C 职员D 职员E 职员F
月薪 (元) 6000 4000 1700 1300 1200 1100 1100 1100
如三毛公司只有8个员工,用上面那种方法你能求出它们工资的中位数是多少吗?独立思考后与同伴交流.
可要动脑筋哟
该公司9员工的工资中出现的频数最多的那个工资,就是他们工资的众数,如:
什么是众数?
1700
6000
4000
1300
1200
1100
500
月薪 6000 4000 1700 1300 1200 1100 500
频数 1 1 1 1 1 3 1
它就是众数
1700
6000
4000
1300
1200
1100
500
月薪 6000 4000 1700 1300 1200 1100 500
频数 1 2 3 1 2 3 1
如果有两个工资的频数并列最多,那么这组数据的众数是什么?独立思考后小组交流.
它是众数
它是众数
如果每个工资数的频数都相同,那么这组数据的众数是什么?独立思考后小组交流.
月薪 6000 4000 1700 1300 1200 1100 500
频数 1 1 1 1 1 1 1
1700
6000
4000
1300
1200
1100
500
这种情况没有众数
工资太低了!找别家吧!
又看到一家电视台在招天气预报员,当时想着我去试试
阿Q又到一家电视台应聘天气预报员,电视台让他把当天(2010年6月9日)的天气预报说一遍,于是阿Q集中精力把我国各大城市的天气预报说了一遍,最后又补说了一句:我国34大城市当日的最高气温(0c)平均数为29度,中位数为30度,众数为31度,你认为阿Q说得对吗?
北京32 天津33 石家庄36 太原
31 呼和浩特27 沈阳
27 长春
26 哈尔滨26 上海
34
南京32 杭州32 合肥32 福州
36 南昌
30 济南
33 郑州
34 武汉
31 长沙
29
广州35 海口35 南宁36 成都
29 重庆
27 贵阳
24 昆明
23 拉萨
21 西安
33
兰州28 银川30 西宁26 乌鲁木齐29 台北
31 香港
36 澳门
35
阿Q说天气预报
他们说我说错了,我当时想回去要好好学习!
1.中位数是一个位置代表值,利用中位数分析数据可以获得一些信息。如果已知一组数据的中位数,那么可以知道,在这组数据中,有一半数比中位数大,有一半数比中位数小.即小于或大于这个中位数的数据各占一半.
2.求中位数的一般步骤:先排序、看奇偶,再确定中位数.
3.中间位置确定确定方法是:
n 为奇数时,中间位置是第 个
n为偶数时,中间位置是第 , 个的平均数
知识要点
如果所有数据出现的次数都一样,那么这组数据没有众数.例如:1,2,3,4,5没有众数.
一般来说,一组数据中,出现次数最多的数就叫这组数据的众数.例如:1,2,3,3,4的众数是3.
如果有两个或两个以上个数出现次数都是最多的,那么这几个数都是这组数据的众数.例如:1,2,2,3,3,4的众数是2和3.
例1 下面两组数据的中位数、众数分别是多少?
(1)5,6,2,3,2
(2)5,6,2,4,3,5
确定中位数要先排序、看奇偶,再确定中位数;确定众数找出现次数最多的数据.
解:(1) 中位数是3,众数是2;
(2)中位数是4.5,众数是5.
提示
例2.已知一组数据10,10,x,8(由大到小排列)的中位数与平均数相等,求x值及这组数据的中位数.
解:∵10,10,x,8的中位数与平均数相等
∴ (10+x)/2=(10+10+x+8)/4
∴x=8
(10+x)/2=9
∴这组数据中的中位数是9.
若没有“由大到小排列”,则情况又如何?
1.中位数、众数的定义及确定方法
中位数:将一组数据按照由小到大的顺序排列,如果数据的个数是奇数,则称处于中间位置的数为这组数据的中位数;如果数据的个数是偶数,则称中间两个数据的平均数为这组数据的中位数.
众数:一组数据中出现次数最多的数据称为这组数据的众数.
课堂小结
2.中位数、众数的意义及作用
中位数是位置代表值,小于或大于这个中位数的数据各占一半;众数往往是人们最为关心的一个量.
3.中位数、众数的区别
中位数是一组数据中唯一的,可能是这组数据中的数据,也可能不是这组数据中的数据;而一组数据中的众数可能不止一个,而且一定是这组数据中的数据.
