20.2 数据的波动程度课件课件课件
图片预览







文档简介
课件21张PPT。20.2 数据的波动程度第1课时 方差复习
导入合作
探究课堂
小结随堂
训练复习回顾:2.何为一组数据的极差?答: 一组数据中的最大值减去最小值所得的差
叫做这组数据的极差.3.极差反映了这组数据哪方面的特征?答:极差反映的是这组数据的变化范围或变化幅度.1.哪些统计量可表示一组数据的集中趋势?答:一组数据的集中趋势可由平均数,众数,中位数表示4.极差有什么局限性?答:极差受极端值的影响较大,不能准确反映数据
的波动情况.跟踪练习一1.在数据统计中,能反映一组数据变化范围大小的指标是( )
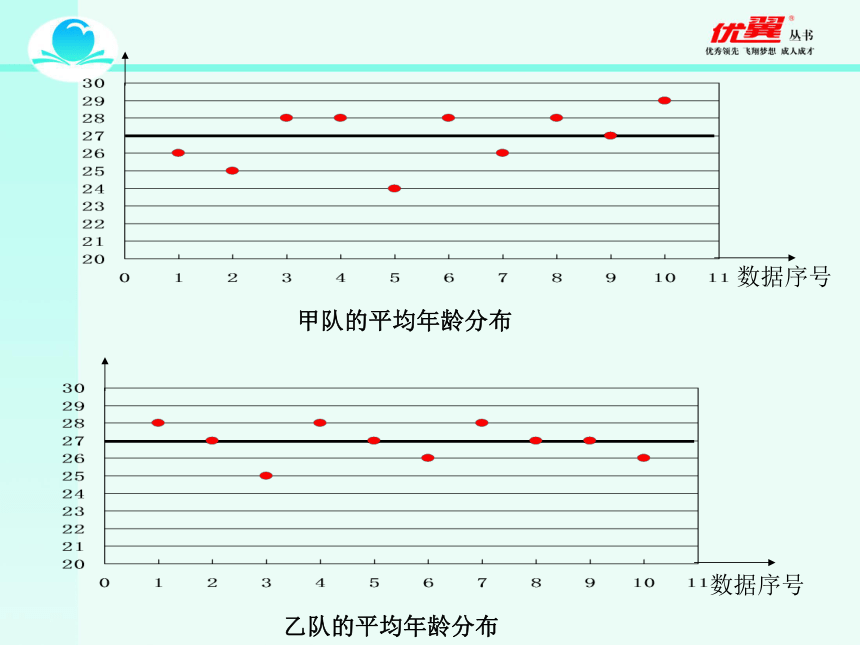
A 平均数 B 众数 C 中位数 D 极差D2.数据 0 , -1 , 3 , 2 , 4 的极差是_____.54.数据 -1 , 3 , 0 , x 的极差是 5 ,则 x =_____.- 2 或 43. 某日最高气温是4 ℃, 温差是 9 ℃,则最低气温是___ ℃.-5上面两组数据的平均数分别是即甲、乙两队参赛选手的平均年龄相同用图表整理这两组数据,分析你画出的图表,看看你能得出哪些结论?活动1甲队的平均年龄分布乙队的平均年龄分布数据序号数据序号比较上面的两幅图可以看出,甲队选手的年龄与其平均年龄的偏差大,乙队选手的年龄较集中地分布在平均年龄左右,那么我们从图中看出的结果能否用一个量来刻画呢?为了刻画一组数据的波动大小,可以采用很多方法,统计中常采用下面的做法:方差越大,数据的波动越大;方差越小,数据的波动就越小来衡量一组数据的波动大小,并把它叫做这组数据的方差(variance),记作s2两组数据的方差分别是:两组数据的平均数是:计算方差的步骤可概括为:
“先平均,后求差,平方后,再平均”.
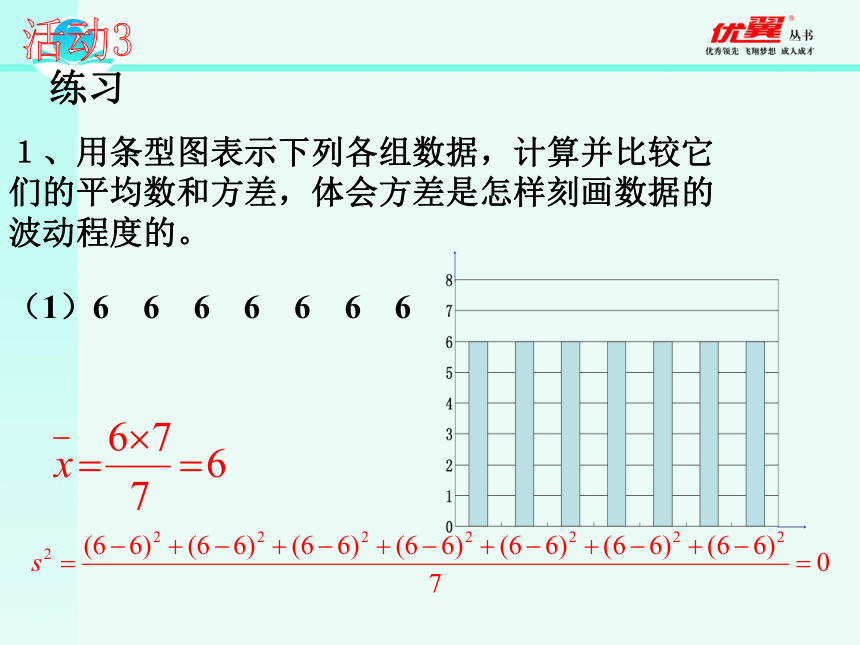
例1 在一次芭蕾舞的比赛中,甲乙两个芭蕾舞团都表演了舞剧(天鹅湖),参加表演的女演员的身高(单位:cm)分别是甲团 163 164 164 165 165 165 166 167乙团 163 164 164 165 166 167 167 168哪个芭蕾舞团的女演员的身高更整齐?解: 甲乙两团演员的平均身高分别是:活动2练习1、用条型图表示下列各组数据,计算并比较它们的平均数和方差,体会方差是怎样刻画数据的波动程度的。(1)6 6 6 6 6 6 6活动3(2)5 5 6 6 6 7 7(3)3 3 4 6 8 9 9(4)3 3 3 6 9 9 91、样本方差的作用是( )
(A)表示总体的平均水平
(B)表示样本的平均水平
(C)准确表示总体的波动大小
(D)表示样本的波动大小 2、样本5、6、7、8、9的方差是 .跟踪练习二D2样本平均数样本容量探索发现1、求这四组数据的平均数、方差。2、对照所填结果,你能从中发现哪些有趣的结论? 3213291830200结论练习16518已知数据a1,a2,a3,…,an的平均数为x,方差为y, 则
①数据a1+3,a2 + 3,a3 +3 ,…,an +3的平均数为 ,
方差为 .
②数据a1-3,a2 -3,a3 -3 ,…,an -3的平均数为 ,
方差为 .
③数据3a1,3a2 ,3a3 ,…,3an的平均数为 ,
方差为 .
④数据2a1-3,2a2 -3,2a3 -3 ,…,2an -3的平均数为 ,方差为 -. x+3yx-3y3x9y2x-34y你能用所发现的结论来解决以下的问题:课堂小结1. 本 节 主 要 知 识 内容?方差越大,数据的波动越大;方差越小,数据的波动就越小来衡量这组数据的波动大小,并把它叫做这组数据的方差(variance),记作s2谈谈自己这节课你学到了什么?1、概念:方差:各数据与平均数的差的平方的平均数叫做这批数据的方差.小结:2、作用:方差用来衡量一批数据的波动大小
(即这批数据偏离平均数的大小).3、在样本容量相同的情况下:
方差越大,说明数据的波动越大,越不稳定.
方差越小,说明数据的波动越小,越稳定.平均数、方差、标准差的几个规律
2、下面是两名跳远运动员的10次测验成绩(单位:m)在这10次测验中,哪名运动员的成绩更稳定?(可以使用计算器)
导入合作
探究课堂
小结随堂
训练复习回顾:2.何为一组数据的极差?答: 一组数据中的最大值减去最小值所得的差
叫做这组数据的极差.3.极差反映了这组数据哪方面的特征?答:极差反映的是这组数据的变化范围或变化幅度.1.哪些统计量可表示一组数据的集中趋势?答:一组数据的集中趋势可由平均数,众数,中位数表示4.极差有什么局限性?答:极差受极端值的影响较大,不能准确反映数据
的波动情况.跟踪练习一1.在数据统计中,能反映一组数据变化范围大小的指标是( )
A 平均数 B 众数 C 中位数 D 极差D2.数据 0 , -1 , 3 , 2 , 4 的极差是_____.54.数据 -1 , 3 , 0 , x 的极差是 5 ,则 x =_____.- 2 或 43. 某日最高气温是4 ℃, 温差是 9 ℃,则最低气温是___ ℃.-5上面两组数据的平均数分别是即甲、乙两队参赛选手的平均年龄相同用图表整理这两组数据,分析你画出的图表,看看你能得出哪些结论?活动1甲队的平均年龄分布乙队的平均年龄分布数据序号数据序号比较上面的两幅图可以看出,甲队选手的年龄与其平均年龄的偏差大,乙队选手的年龄较集中地分布在平均年龄左右,那么我们从图中看出的结果能否用一个量来刻画呢?为了刻画一组数据的波动大小,可以采用很多方法,统计中常采用下面的做法:方差越大,数据的波动越大;方差越小,数据的波动就越小来衡量一组数据的波动大小,并把它叫做这组数据的方差(variance),记作s2两组数据的方差分别是:两组数据的平均数是:计算方差的步骤可概括为:
“先平均,后求差,平方后,再平均”.
例1 在一次芭蕾舞的比赛中,甲乙两个芭蕾舞团都表演了舞剧(天鹅湖),参加表演的女演员的身高(单位:cm)分别是甲团 163 164 164 165 165 165 166 167乙团 163 164 164 165 166 167 167 168哪个芭蕾舞团的女演员的身高更整齐?解: 甲乙两团演员的平均身高分别是:活动2练习1、用条型图表示下列各组数据,计算并比较它们的平均数和方差,体会方差是怎样刻画数据的波动程度的。(1)6 6 6 6 6 6 6活动3(2)5 5 6 6 6 7 7(3)3 3 4 6 8 9 9(4)3 3 3 6 9 9 91、样本方差的作用是( )
(A)表示总体的平均水平
(B)表示样本的平均水平
(C)准确表示总体的波动大小
(D)表示样本的波动大小 2、样本5、6、7、8、9的方差是 .跟踪练习二D2样本平均数样本容量探索发现1、求这四组数据的平均数、方差。2、对照所填结果,你能从中发现哪些有趣的结论? 3213291830200结论练习16518已知数据a1,a2,a3,…,an的平均数为x,方差为y, 则
①数据a1+3,a2 + 3,a3 +3 ,…,an +3的平均数为 ,
方差为 .
②数据a1-3,a2 -3,a3 -3 ,…,an -3的平均数为 ,
方差为 .
③数据3a1,3a2 ,3a3 ,…,3an的平均数为 ,
方差为 .
④数据2a1-3,2a2 -3,2a3 -3 ,…,2an -3的平均数为 ,方差为 -. x+3yx-3y3x9y2x-34y你能用所发现的结论来解决以下的问题:课堂小结1. 本 节 主 要 知 识 内容?方差越大,数据的波动越大;方差越小,数据的波动就越小来衡量这组数据的波动大小,并把它叫做这组数据的方差(variance),记作s2谈谈自己这节课你学到了什么?1、概念:方差:各数据与平均数的差的平方的平均数叫做这批数据的方差.小结:2、作用:方差用来衡量一批数据的波动大小
(即这批数据偏离平均数的大小).3、在样本容量相同的情况下:
方差越大,说明数据的波动越大,越不稳定.
方差越小,说明数据的波动越小,越稳定.平均数、方差、标准差的几个规律
2、下面是两名跳远运动员的10次测验成绩(单位:m)在这10次测验中,哪名运动员的成绩更稳定?(可以使用计算器)
