20.2 数据的波动程度课件
图片预览








文档简介
课件21张PPT。20.2 数据的波动程度第2课时 根据方差做决策复习
导入合作
探究课堂
小结随堂
训练2.方差的计算公式: ,方差越大, 越大;方差越小, 越小.数据的波动数据的波动1.下列统计量中,能反映一名同学在7-9年级学段的学习成绩稳定程度的是( )
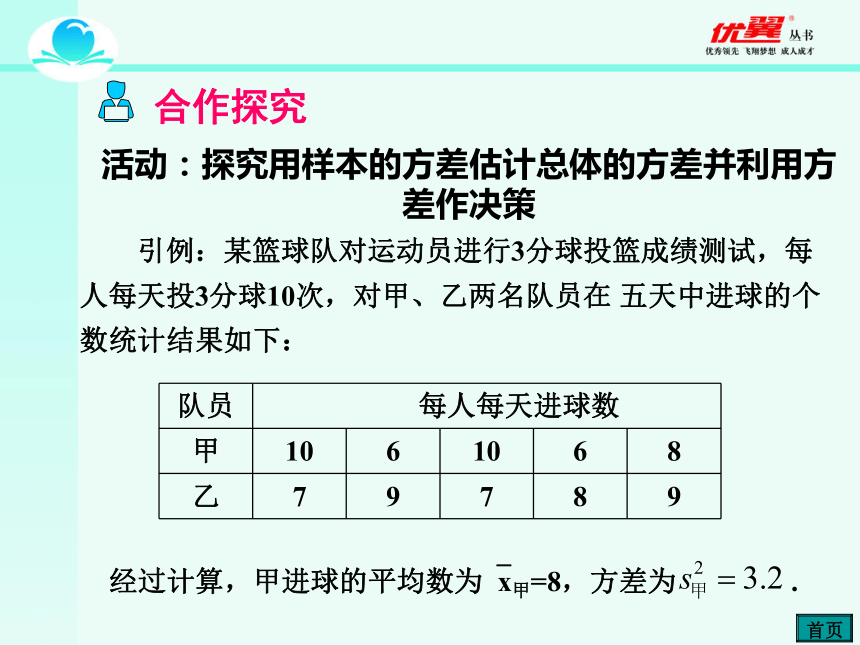
A. 平均数 B.中位数 C.众数 D.方差D3.在方差的计算公式 中,数字10和20分别表示( )A.样本的容量和方差B.平均数和样本的容量C.样本的容量和平均数D.样本的方差和平均数C复习导入4.已知一组数据-2,-1,0,x,1的平均数是0,那么这组数据的方差是 . 5.甲、乙两名战士在射击训练中,打靶的次数相同,且打中环数的平均数 ,如果甲的射击成绩比较稳定,那么方差的大小关系是 S2甲 S2乙。2< 引例:某篮球队对运动员进行3分球投篮成绩测试,每人每天投3分球10次,对甲、乙两名队员在 五天中进球的个数统计结果如下: 经过计算,甲进球的平均数为?x甲=8,方差为 .
合作探究活动:探究用样本的方差估计总体的方差并利用方差作决策(1)求乙进球的平均数和方差;
(2)现在需要根据以上结果,从甲、乙两名队员中选出一人去参加3分球投篮大赛,你认为应该选哪名队员去?为什么?
(1)在解决实际问题时,方差的作用是什么?
反映数据的波动大小.
方差越大,数据的波动越大;方差越小,数据的波动越
小,可用样本方差估计总体方差.
(2)运用方差解决实际问题的一般步骤是怎样的?
先计算样本数据平均数,当两组数据的平均数相等或相
近时,再利用样本方差来估计总体数据的波动情况.知识要点 例1 某农民几年前承包了甲、乙两片荒山,各栽了100棵蜜橘,成活98%,现已挂果,经济效益显著,为了分析经营情况,他从甲山随意采摘了4棵树上的蜜橘称得质量分别为25,18,20,21千克;他从乙山随意采摘了4棵树上的蜜橘,称得质量分别为21,24,19,20千克.如下表:(1)4+4=8;解:(1)样本容量是多少?(2)样本平均数是多少?并估算出甲、乙两山蜜橘
的总产量? 解:x甲=21, ?x乙=21(3)甲、乙两山哪个山上蜜橘长势较整齐?__例2:为了从甲、乙两名学生中选择一人去参加电脑知识竞赛,在相同条件下对他们的电脑知识进行10次测验,成绩(单位:分)如下:(1)填写下表:84900.514.4(2)利用以上信息,请从不同的角度对甲、乙两名同学的成绩进行评价从众数看,甲成绩的众数为84分,乙成绩的众数是90分,乙的成绩比甲好;
从方差看,s2甲=14.4, s2乙=34,甲的成绩比乙相对稳定;
从甲、乙的中位数、平均数看,中位数、平均数都是84分,两人成绩一样好;
从频率看,甲85分以上的次数比乙少,乙的成绩比甲好。例3:甲、乙两人在相同条件下各射靶10次,
每次射靶的成绩情况如图所示:(1)填写下表:(2)请从下列四个不同的角度对这次测试结果进行分析:
①从平均数和方差相结合看(分析谁的成绩更稳定)
②从平均数和中位数相结合看(分析谁的成绩好些)
③从平均数和命中9环以上的次数相结合看(分析谁的成绩好些)
④从折线图上的两人射击命中环数走势看(分析谁更有潜力)777.53(2)(1)甲的成绩在平均数上下波动,而乙处于上升趋势,从第四次以后就没有比甲少的情况发生,所以乙较有潜力。例4:一次科技知识竞赛,两组学生成绩统计如下:已经算得两个组的人平均分都是80分,请根据你所
学过的统计知识,进一步判断这两个组在这次竞赛
中的成绩谁优谁劣,并说明理由.解: (1)甲组成绩的众数为90分,乙组成绩的众数为70分, 以成绩的众数比较看,甲组成绩好些.(3)甲、乙两组成绩的中位数都是80分,甲组成绩在中位数以上(包括中位数)的人有33人,乙组成绩在中位数以上(包括中位数)的人有26人,从这一角度,看甲组成绩总体较好;
(4)从成绩统计表看,甲组成绩高于80分的人数为20人,乙组成绩高于80分的人数为24人,乙组成绩集中在高分段的人数多,同时,乙组得满分的人数比甲组得满分的人数多6人,从这一角度看,乙组的成绩较好.
练习某快餐公司的香辣鸡腿很受消费者欢迎,为了保持公司信誉,公司严把鸡腿的进货质量,现有甲、乙两家农副产品加工厂到快餐公司推销鸡腿,两家鸡腿的价格相同,品质相近,快餐公司决定通过检查鸡腿的重量来确定选购哪家公司的鸡腿,检查人员以两家的鸡腿中各抽取15个鸡腿,记录它们的质量如下(单位:g):甲 74 74 75 74 76 73 76 73 76 75 78 77 74 72 73乙 75 73 79 72 76 71 73 7278 74 77 78 80 71 75根据上面的数据,你认为快餐公司应该选购哪家加工厂的鸡腿?因为 ,所以选择甲厂鸡腿加工。 用样估计总体是统计的基本思想,正像用样本平均数估计总体平均数一样,考察总体方差时,如果所要考察的总体包含很多个体,或者考察本身带有破坏性,实际常常用样本的方差来估计总体的方差.1.在什么情况下要用样本的方差估总体方差?2.用样本的方差估总体方差要注意什么? 当两组数据的平均数相等或相近时,才利用方差来判断它们的波动情况. 课堂小结平均数、方差、标准差的几个规律练习16518已知数据a1,a2,a3,…,an的平均数为x,方差为y, 则
①数据a1+3,a2 + 3,a3 +3 ,…,an +3的平均数为 ,
方差为 .
②数据a1-3,a2 -3,a3 -3 ,…,an -3的平均数为 ,
方差为 .
③数据3a1,3a2 ,3a3 ,…,3an的平均数为 ,
方差为 .
④数据2a1-3,2a2 -3,2a3 -3 ,…,2an -3的平均数为 ,方差为 -. x+3yx-3y3x9y2x-34y你能用所发现的结论来解决以下的问题:
导入合作
探究课堂
小结随堂
训练2.方差的计算公式: ,方差越大, 越大;方差越小, 越小.数据的波动数据的波动1.下列统计量中,能反映一名同学在7-9年级学段的学习成绩稳定程度的是( )
A. 平均数 B.中位数 C.众数 D.方差D3.在方差的计算公式 中,数字10和20分别表示( )A.样本的容量和方差B.平均数和样本的容量C.样本的容量和平均数D.样本的方差和平均数C复习导入4.已知一组数据-2,-1,0,x,1的平均数是0,那么这组数据的方差是 . 5.甲、乙两名战士在射击训练中,打靶的次数相同,且打中环数的平均数 ,如果甲的射击成绩比较稳定,那么方差的大小关系是 S2甲 S2乙。2< 引例:某篮球队对运动员进行3分球投篮成绩测试,每人每天投3分球10次,对甲、乙两名队员在 五天中进球的个数统计结果如下: 经过计算,甲进球的平均数为?x甲=8,方差为 .
合作探究活动:探究用样本的方差估计总体的方差并利用方差作决策(1)求乙进球的平均数和方差;
(2)现在需要根据以上结果,从甲、乙两名队员中选出一人去参加3分球投篮大赛,你认为应该选哪名队员去?为什么?
(1)在解决实际问题时,方差的作用是什么?
反映数据的波动大小.
方差越大,数据的波动越大;方差越小,数据的波动越
小,可用样本方差估计总体方差.
(2)运用方差解决实际问题的一般步骤是怎样的?
先计算样本数据平均数,当两组数据的平均数相等或相
近时,再利用样本方差来估计总体数据的波动情况.知识要点 例1 某农民几年前承包了甲、乙两片荒山,各栽了100棵蜜橘,成活98%,现已挂果,经济效益显著,为了分析经营情况,他从甲山随意采摘了4棵树上的蜜橘称得质量分别为25,18,20,21千克;他从乙山随意采摘了4棵树上的蜜橘,称得质量分别为21,24,19,20千克.如下表:(1)4+4=8;解:(1)样本容量是多少?(2)样本平均数是多少?并估算出甲、乙两山蜜橘
的总产量? 解:x甲=21, ?x乙=21(3)甲、乙两山哪个山上蜜橘长势较整齐?__例2:为了从甲、乙两名学生中选择一人去参加电脑知识竞赛,在相同条件下对他们的电脑知识进行10次测验,成绩(单位:分)如下:(1)填写下表:84900.514.4(2)利用以上信息,请从不同的角度对甲、乙两名同学的成绩进行评价从众数看,甲成绩的众数为84分,乙成绩的众数是90分,乙的成绩比甲好;
从方差看,s2甲=14.4, s2乙=34,甲的成绩比乙相对稳定;
从甲、乙的中位数、平均数看,中位数、平均数都是84分,两人成绩一样好;
从频率看,甲85分以上的次数比乙少,乙的成绩比甲好。例3:甲、乙两人在相同条件下各射靶10次,
每次射靶的成绩情况如图所示:(1)填写下表:(2)请从下列四个不同的角度对这次测试结果进行分析:
①从平均数和方差相结合看(分析谁的成绩更稳定)
②从平均数和中位数相结合看(分析谁的成绩好些)
③从平均数和命中9环以上的次数相结合看(分析谁的成绩好些)
④从折线图上的两人射击命中环数走势看(分析谁更有潜力)777.53(2)(1)甲的成绩在平均数上下波动,而乙处于上升趋势,从第四次以后就没有比甲少的情况发生,所以乙较有潜力。例4:一次科技知识竞赛,两组学生成绩统计如下:已经算得两个组的人平均分都是80分,请根据你所
学过的统计知识,进一步判断这两个组在这次竞赛
中的成绩谁优谁劣,并说明理由.解: (1)甲组成绩的众数为90分,乙组成绩的众数为70分, 以成绩的众数比较看,甲组成绩好些.(3)甲、乙两组成绩的中位数都是80分,甲组成绩在中位数以上(包括中位数)的人有33人,乙组成绩在中位数以上(包括中位数)的人有26人,从这一角度,看甲组成绩总体较好;
(4)从成绩统计表看,甲组成绩高于80分的人数为20人,乙组成绩高于80分的人数为24人,乙组成绩集中在高分段的人数多,同时,乙组得满分的人数比甲组得满分的人数多6人,从这一角度看,乙组的成绩较好.
练习某快餐公司的香辣鸡腿很受消费者欢迎,为了保持公司信誉,公司严把鸡腿的进货质量,现有甲、乙两家农副产品加工厂到快餐公司推销鸡腿,两家鸡腿的价格相同,品质相近,快餐公司决定通过检查鸡腿的重量来确定选购哪家公司的鸡腿,检查人员以两家的鸡腿中各抽取15个鸡腿,记录它们的质量如下(单位:g):甲 74 74 75 74 76 73 76 73 76 75 78 77 74 72 73乙 75 73 79 72 76 71 73 7278 74 77 78 80 71 75根据上面的数据,你认为快餐公司应该选购哪家加工厂的鸡腿?因为 ,所以选择甲厂鸡腿加工。 用样估计总体是统计的基本思想,正像用样本平均数估计总体平均数一样,考察总体方差时,如果所要考察的总体包含很多个体,或者考察本身带有破坏性,实际常常用样本的方差来估计总体的方差.1.在什么情况下要用样本的方差估总体方差?2.用样本的方差估总体方差要注意什么? 当两组数据的平均数相等或相近时,才利用方差来判断它们的波动情况. 课堂小结平均数、方差、标准差的几个规律练习16518已知数据a1,a2,a3,…,an的平均数为x,方差为y, 则
①数据a1+3,a2 + 3,a3 +3 ,…,an +3的平均数为 ,
方差为 .
②数据a1-3,a2 -3,a3 -3 ,…,an -3的平均数为 ,
方差为 .
③数据3a1,3a2 ,3a3 ,…,3an的平均数为 ,
方差为 .
④数据2a1-3,2a2 -3,2a3 -3 ,…,2an -3的平均数为 ,方差为 -. x+3yx-3y3x9y2x-34y你能用所发现的结论来解决以下的问题:
