2025年湖南省长沙市中考数学信息试卷(一)(含答案)
文档属性
| 名称 | 2025年湖南省长沙市中考数学信息试卷(一)(含答案) |  | |
| 格式 | docx | ||
| 文件大小 | 236.4KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2025-05-29 19:09:55 | ||
图片预览



文档简介
2025年湖南省长沙市中考数学信息试卷(一)
一、选择题:本题共10小题,每小题3分,共30分。在每小题给出的选项中,只有一项是符合题目要求的。
1.九章算术是我国古代数学经典著作,其中“方程术”最早引入“负数”,用正、负数表示相反意义的量若跳远测试以米为基准,跳米记作米,那么跳米应记作( )
A. 米 B. 米 C. 米 D. 米
2.科学研究估算,长沙洋湖湿地公园生态系统中约有,,,,个微生物若用科学记数法表示该数量,正确选项是( )
A. B. C. D.
3.未来乃可预见之时代,寰宇知名人工智能企业徽标林立,请问下列图示中,属中心对称而非轴对称者为几何( )
A. B.
C. D.
4.在湖南师大附中梅溪湖中学第四届校园歌手大赛中,某组参赛选手得分如下单位:分:,,,,,,,则该组参赛选手得分的中位数是多少分( )
A. 分 B. 分 C. 分 D. 分
5.在下列调查中,适宜采用普查的是( )
A. 调查某神舟号火箭的零件安全情况 B. 调查长沙县中小学生心理健康情况
C. 调查橘子洲头游园日均客流量 D. 调查新闻联播栏目的收视率
6.已知点,,在同一个函数图象上,则这个函数图象可能是( )
A. B. C. D.
7.如图,直线,点在直线上,点在直线上,连接过点作,交直线于点若,则的度数为( )
A. B. C. D.
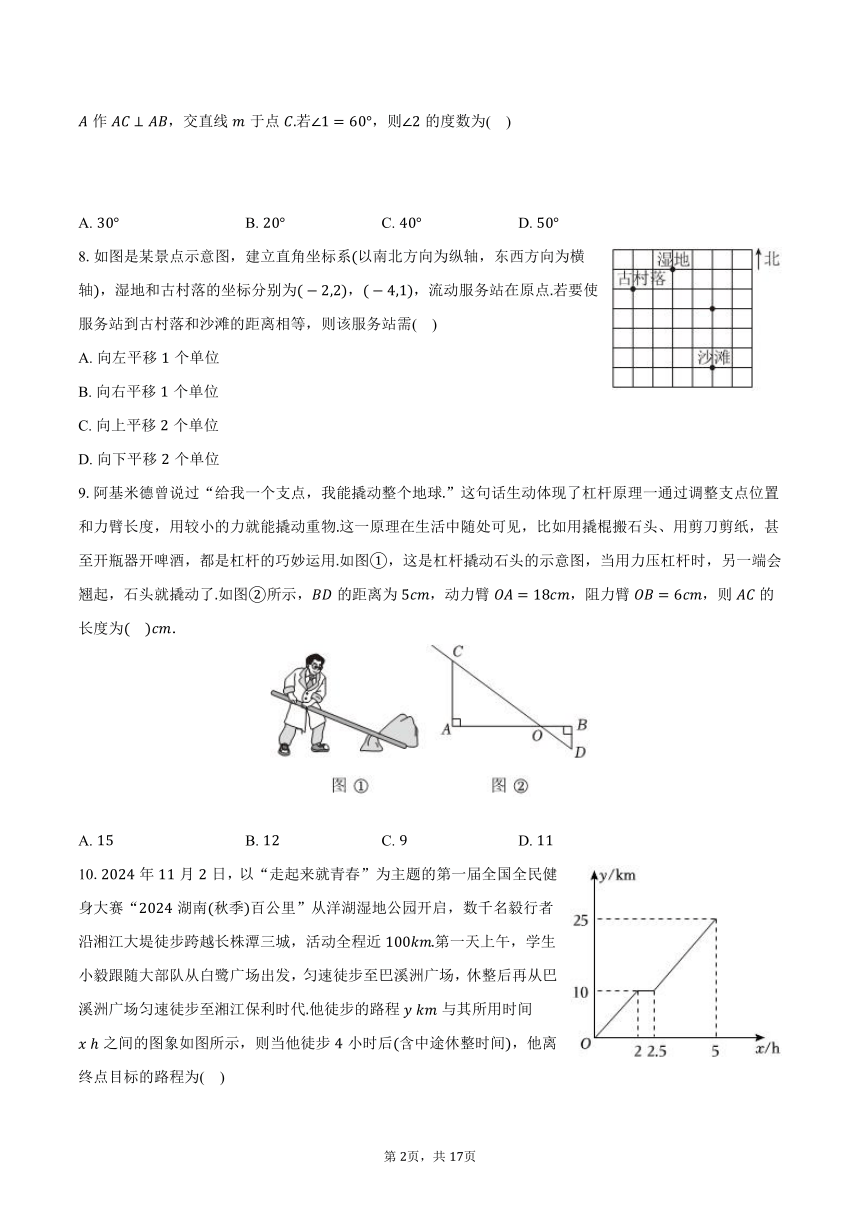
8.如图是某景点示意图,建立直角坐标系以南北方向为纵轴,东西方向为横轴,湿地和古村落的坐标分别为,,流动服务站在原点若要使服务站到古村落和沙滩的距离相等,则该服务站需( )
A. 向左平移个单位
B. 向右平移个单位
C. 向上平移个单位
D. 向下平移个单位
9.阿基米德曾说过“给我一个支点,我能撬动整个地球”这句话生动体现了杠杆原理一通过调整支点位置和力臂长度,用较小的力就能撬动重物这一原理在生活中随处可见,比如用撬棍搬石头、用剪刀剪纸,甚至开瓶器开啤酒,都是杠杆的巧妙运用如图,这是杠杆撬动石头的示意图,当用力压杠杆时,另一端会翘起,石头就撬动了如图所示,的距离为,动力臂,阻力臂,则的长度为.
A. B. C. D.
10.年月日,以“走起来就青春”为主题的第一届全国全民健身大赛“湖南秋季百公里”从洋湖湿地公园开启,数千名毅行者沿湘江大堤徒步跨越长株潭三城,活动全程近第一天上午,学生小毅跟随大部队从白鹭广场出发,匀速徒步至巴溪洲广场,休整后再从巴溪洲广场匀速徒步至湘江保利时代他徒步的路程与其所用时间之间的图象如图所示,则当他徒步小时后含中途休整时间,他离终点目标的路程为( )
A. B. C. D.
二、填空题:本题共6小题,每小题3分,共18分。
11.若要使分式有意义,则的取值范围是______.
12.若,则 ______.
13.已知一个山坡的坡度为:,则山坡的坡角为______.
14.一个不透明的布袋里装有个红球,个黄球,个白球,个黑球,它们除颜色外其余都相同,从袋中任意摸出个球,是黄球的概率为______.
15.如图,点在反比例函数的图象上,轴于点,的面积为,则的值为______.
16.如图,在平行四边形中,延长到点,连接,使若,则的度数为______.
三、计算题:本大题共1小题,共6分。
17.先化简,再求值:,其中.
四、解答题:本题共8小题,共66分。解答应写出文字说明,证明过程或演算步骤。
18.本小题分
计算:.
19.本小题分
我国生产的无人机畅销世界,树立了良好的品牌形象,在一座高架桥的修建过程中,需要测量一条河的宽度,工作人员使用无人飞机通过设备在处测得,两处的俯角分别为和,测得无人机离水平地面的高度为米,若,,三点在同一条水平直线上,则这条河的宽度为多少米?参考数据:,,结果保留整数
20.本小题分
如图,中,的垂直平分线交于点,交于点,为中点,.
求证:;
若,求的度数.
21.本小题分
在中,,,利用尺规作图在边上求作一点,使得∽不写作法,保留作图痕迹
22.本小题分
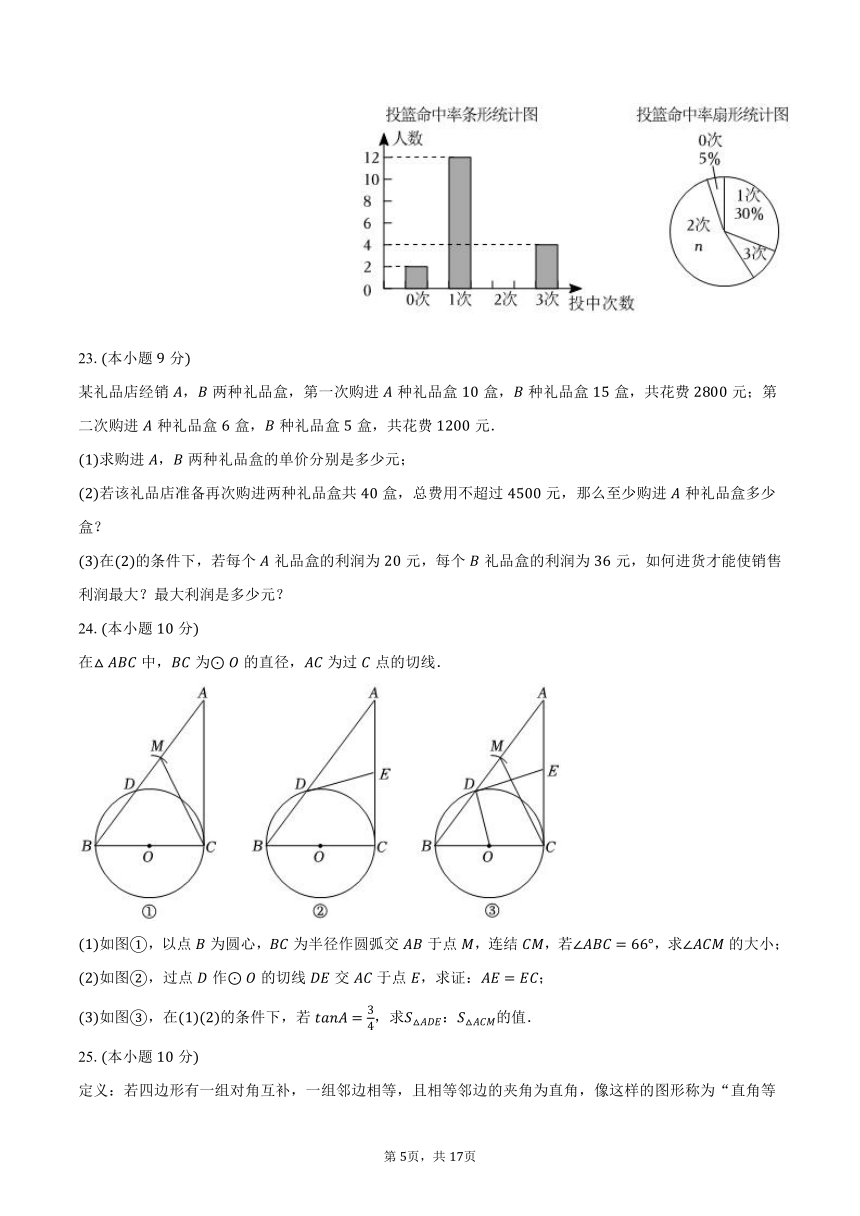
为落实“双减”政策,增强学生体质,阳光中学积极开展体育健身活动了解初三学生的投篮命中率,组织了初三学生定点投篮,规定每人投篮次现对初三班每名学生投中的次数进行统计,绘制成如下的两幅统计图,根据图中提供的信息,回答下列问题.
初三班的学生投中次的人数为人,扇形统计图中 ______;
扇形统计图中“次”对应的圆心角的度数为______;
在投中次的学生中,有名男生名女生,现要抽调两名学生参加学校投篮比赛,请用画树状图或列表的方法,求恰好抽到名男生的概率.
23.本小题分
某礼品店经销,两种礼品盒,第一次购进种礼品盒盒,种礼品盒盒,共花费元;第二次购进种礼品盒盒,种礼品盒盒,共花费元.
求购进,两种礼品盒的单价分别是多少元;
若该礼品店准备再次购进两种礼品盒共盒,总费用不超过元,那么至少购进种礼品盒多少盒?
在的条件下,若每个礼品盒的利润为元,每个礼品盒的利润为元,如何进货才能使销售利润最大?最大利润是多少元?
24.本小题分
在中,为的直径,为过点的切线.
如图,以点为圆心,为半径作圆弧交于点,连结,若,求的大小;
如图,过点作的切线交于点,求证:;
如图,在的条件下,若,求:的值.
25.本小题分
定义:若四边形有一组对角互补,一组邻边相等,且相等邻边的夹角为直角,像这样的图形称为“直角等邻对补”四边形,简称“直等补”四边形.
根据以上定义,解决下列问题:
如图,正方形中,是上的点,将绕点旋转,使与重合,此时点的对应点在的延长线上,则四边形为“直等补”四边形,为什么?
如图,已知四边形是“直等补”四边形,,,,点到直线的距离为.
求的长;
若、分别是、边上的动点,求周长的最小值.
答案和解析
1.【答案】
【解析】若跳远测试以米为基准,跳米记作米,那么跳米应记作米,
故选:.
2.【答案】
【解析】.
故选:.
3.【答案】
【解析】既不是轴对称图形,也不是中心对称图形,故此选项不符合题意;
B.不是轴对称图形,是中心对称图形,故此选项符合题意;
C.既是轴对称图形,又是中心对称图形,故此选项不符合题意;
D.是轴对称图形,不是中心对称图形,故此选项不符合题意;
故选:.
4.【答案】
【解析】一共有个数据,从小到大排序为:,,,,,,,
中位数为第个数,即为,
故选:.
5.【答案】
【解析】调查某神舟号火箭的零件安全情况,适宜采用普查,故A符合题意;
B.调查长沙县中小学生心理健康情况,适宜采用抽样调查,故B不符合题意;
C.调查橘子洲头游园日均客流量,适宜采用抽样调查,故C不符合题意;
D.调查新闻联播栏目的收视率,适宜采用抽样调查,故D不符合题意;
故选:.
6.【答案】
【解析】点,,
与关于轴对称,
即这个函数图象关于轴对称,故选项A,不符合题意;
,,
当时,随的增大而减小,故选项B符合题意,选项D不符合题意.
故选:.
7.【答案】
【解析】如图,
,
,
,,
,
,
故选:.
8.【答案】
【解析】湿地和古村落的坐标分别为,,
坐标原点在沙滩北个单位处,
若要使服务站到古村落和沙滩的距离相等,服务站需向左平移个单位即可.
故选:.
9.【答案】
【解析】,,
,
∽,
,
的距离为,动力臂,阻力臂,
,
,
的长为.
故选:.
10.【答案】
【解析】由题意得:从白鹭广场出发,匀速徒步至巴溪洲广场的速度为千米小时,
休整后再从巴溪洲广场匀速徒步至湘江保利时代的速度为千米小时,
当他徒步小时后含中途休整时间徒步的路程为千米,
他离终点目标的路程为千米.
故选:.
11.【答案】
【解析】分式有意义,
,
解得,,
故答案为:.
12.【答案】
【解析】两边都乘以,得
,
解得,
经检验是原方程的解,
所以原方程的解为.
故答案为:.
13.【答案】
【解析】设坡角为,已知一个山坡的坡度为:,
由题意得,,
.
故答案为:.
14.【答案】
【解析】一个不透明的布袋里装有个红球,个黄球,个白球,个黑球,
袋中球的总数为,
从袋中任意摸出个球,是黄球的概率为.
故答案为:.
15.【答案】
【解析】根据反比例函数系数的几何意义可知,,
即,
解得:;
函数图象位于第一、三象限,
,
故,
故答案为:.
16.【答案】
【解析】四边形是平行四边形,,
,
已知,
等边对等角,
即的度数为.
故答案为:.
17.【答案】原式
,
当时,
原式.
18.【答案】.
【解析】
.
19.【答案】,
,,
,
米,
在中,
,
米,
米.
答:米.
20.【答案】证明:如图,连接,
的垂直平分线交于点,
,
,
,
为中点,
;
,,
,
,
,
,
.
21.【答案】,,
,
是公共角,
只要作即可,
恰好,
作的角平分线即可.
如图所示:∽.
22.【解析】九年级班的学生人数人,
投中次的人数为:人,
扇形统计图中,
故答案为:;
,
故答案为:;
如下:
由图可知,共有种等可能的情况,其中恰好抽到名男生的情况有种,
,
概率是.
23.【解析】设购进种礼品盒的单价是元,种礼品盒的单价是元,
由题意得:,
解得:,
答:购进种礼品盒的单价是元,种礼品盒的单价是元;
设购进种礼品盒盒,则购进种礼品盒盒,
由题意得:,
解得:,
答:至少购进种礼品盒盒;
设销售利润为元,
由题意得:,
,
随的增大而减小,
当时,有最大值,最大值,
此时,,
答:购进种礼品盒盒,种礼品盒盒才能使销售利润最大,最大利润是元.
24.【解析】由题意知,,
,
,
,
;
证明:连接,
为的直径,
,
为过点的切线,
过点作的切线交于点,
,
,
,,
,
,
;
连接,
由可得,,,
,
设,,则,
,
,,
,
,
,,
::.
25.【答案】四边形是正方形,
,
将绕点旋转,使与重合,此时点的对应点在的延长线上,
,,
,
,
四边形为“直等补”四边形;
过作于点,如图,
则,
四边形是“直等补”四边形,,,,
,,
,
,
,
四边形是矩形,
,
,
,
,,
≌,
,
设,则,
,
,
解得,,或舍,
;
如图,延长到,使得,延长到,使得,连接,分别与、交于点、,过作,与的延长线交于点.
则,,
,
,,
的周长的值最小,
四边形是“直等补”四边形,
,
,
,
,
∽,
,
,,
,
,
,,
,
,
周长的最小值为.
第11页,共17页
一、选择题:本题共10小题,每小题3分,共30分。在每小题给出的选项中,只有一项是符合题目要求的。
1.九章算术是我国古代数学经典著作,其中“方程术”最早引入“负数”,用正、负数表示相反意义的量若跳远测试以米为基准,跳米记作米,那么跳米应记作( )
A. 米 B. 米 C. 米 D. 米
2.科学研究估算,长沙洋湖湿地公园生态系统中约有,,,,个微生物若用科学记数法表示该数量,正确选项是( )
A. B. C. D.
3.未来乃可预见之时代,寰宇知名人工智能企业徽标林立,请问下列图示中,属中心对称而非轴对称者为几何( )
A. B.
C. D.
4.在湖南师大附中梅溪湖中学第四届校园歌手大赛中,某组参赛选手得分如下单位:分:,,,,,,,则该组参赛选手得分的中位数是多少分( )
A. 分 B. 分 C. 分 D. 分
5.在下列调查中,适宜采用普查的是( )
A. 调查某神舟号火箭的零件安全情况 B. 调查长沙县中小学生心理健康情况
C. 调查橘子洲头游园日均客流量 D. 调查新闻联播栏目的收视率
6.已知点,,在同一个函数图象上,则这个函数图象可能是( )
A. B. C. D.
7.如图,直线,点在直线上,点在直线上,连接过点作,交直线于点若,则的度数为( )
A. B. C. D.
8.如图是某景点示意图,建立直角坐标系以南北方向为纵轴,东西方向为横轴,湿地和古村落的坐标分别为,,流动服务站在原点若要使服务站到古村落和沙滩的距离相等,则该服务站需( )
A. 向左平移个单位
B. 向右平移个单位
C. 向上平移个单位
D. 向下平移个单位
9.阿基米德曾说过“给我一个支点,我能撬动整个地球”这句话生动体现了杠杆原理一通过调整支点位置和力臂长度,用较小的力就能撬动重物这一原理在生活中随处可见,比如用撬棍搬石头、用剪刀剪纸,甚至开瓶器开啤酒,都是杠杆的巧妙运用如图,这是杠杆撬动石头的示意图,当用力压杠杆时,另一端会翘起,石头就撬动了如图所示,的距离为,动力臂,阻力臂,则的长度为.
A. B. C. D.
10.年月日,以“走起来就青春”为主题的第一届全国全民健身大赛“湖南秋季百公里”从洋湖湿地公园开启,数千名毅行者沿湘江大堤徒步跨越长株潭三城,活动全程近第一天上午,学生小毅跟随大部队从白鹭广场出发,匀速徒步至巴溪洲广场,休整后再从巴溪洲广场匀速徒步至湘江保利时代他徒步的路程与其所用时间之间的图象如图所示,则当他徒步小时后含中途休整时间,他离终点目标的路程为( )
A. B. C. D.
二、填空题:本题共6小题,每小题3分,共18分。
11.若要使分式有意义,则的取值范围是______.
12.若,则 ______.
13.已知一个山坡的坡度为:,则山坡的坡角为______.
14.一个不透明的布袋里装有个红球,个黄球,个白球,个黑球,它们除颜色外其余都相同,从袋中任意摸出个球,是黄球的概率为______.
15.如图,点在反比例函数的图象上,轴于点,的面积为,则的值为______.
16.如图,在平行四边形中,延长到点,连接,使若,则的度数为______.
三、计算题:本大题共1小题,共6分。
17.先化简,再求值:,其中.
四、解答题:本题共8小题,共66分。解答应写出文字说明,证明过程或演算步骤。
18.本小题分
计算:.
19.本小题分
我国生产的无人机畅销世界,树立了良好的品牌形象,在一座高架桥的修建过程中,需要测量一条河的宽度,工作人员使用无人飞机通过设备在处测得,两处的俯角分别为和,测得无人机离水平地面的高度为米,若,,三点在同一条水平直线上,则这条河的宽度为多少米?参考数据:,,结果保留整数
20.本小题分
如图,中,的垂直平分线交于点,交于点,为中点,.
求证:;
若,求的度数.
21.本小题分
在中,,,利用尺规作图在边上求作一点,使得∽不写作法,保留作图痕迹
22.本小题分
为落实“双减”政策,增强学生体质,阳光中学积极开展体育健身活动了解初三学生的投篮命中率,组织了初三学生定点投篮,规定每人投篮次现对初三班每名学生投中的次数进行统计,绘制成如下的两幅统计图,根据图中提供的信息,回答下列问题.
初三班的学生投中次的人数为人,扇形统计图中 ______;
扇形统计图中“次”对应的圆心角的度数为______;
在投中次的学生中,有名男生名女生,现要抽调两名学生参加学校投篮比赛,请用画树状图或列表的方法,求恰好抽到名男生的概率.
23.本小题分
某礼品店经销,两种礼品盒,第一次购进种礼品盒盒,种礼品盒盒,共花费元;第二次购进种礼品盒盒,种礼品盒盒,共花费元.
求购进,两种礼品盒的单价分别是多少元;
若该礼品店准备再次购进两种礼品盒共盒,总费用不超过元,那么至少购进种礼品盒多少盒?
在的条件下,若每个礼品盒的利润为元,每个礼品盒的利润为元,如何进货才能使销售利润最大?最大利润是多少元?
24.本小题分
在中,为的直径,为过点的切线.
如图,以点为圆心,为半径作圆弧交于点,连结,若,求的大小;
如图,过点作的切线交于点,求证:;
如图,在的条件下,若,求:的值.
25.本小题分
定义:若四边形有一组对角互补,一组邻边相等,且相等邻边的夹角为直角,像这样的图形称为“直角等邻对补”四边形,简称“直等补”四边形.
根据以上定义,解决下列问题:
如图,正方形中,是上的点,将绕点旋转,使与重合,此时点的对应点在的延长线上,则四边形为“直等补”四边形,为什么?
如图,已知四边形是“直等补”四边形,,,,点到直线的距离为.
求的长;
若、分别是、边上的动点,求周长的最小值.
答案和解析
1.【答案】
【解析】若跳远测试以米为基准,跳米记作米,那么跳米应记作米,
故选:.
2.【答案】
【解析】.
故选:.
3.【答案】
【解析】既不是轴对称图形,也不是中心对称图形,故此选项不符合题意;
B.不是轴对称图形,是中心对称图形,故此选项符合题意;
C.既是轴对称图形,又是中心对称图形,故此选项不符合题意;
D.是轴对称图形,不是中心对称图形,故此选项不符合题意;
故选:.
4.【答案】
【解析】一共有个数据,从小到大排序为:,,,,,,,
中位数为第个数,即为,
故选:.
5.【答案】
【解析】调查某神舟号火箭的零件安全情况,适宜采用普查,故A符合题意;
B.调查长沙县中小学生心理健康情况,适宜采用抽样调查,故B不符合题意;
C.调查橘子洲头游园日均客流量,适宜采用抽样调查,故C不符合题意;
D.调查新闻联播栏目的收视率,适宜采用抽样调查,故D不符合题意;
故选:.
6.【答案】
【解析】点,,
与关于轴对称,
即这个函数图象关于轴对称,故选项A,不符合题意;
,,
当时,随的增大而减小,故选项B符合题意,选项D不符合题意.
故选:.
7.【答案】
【解析】如图,
,
,
,,
,
,
故选:.
8.【答案】
【解析】湿地和古村落的坐标分别为,,
坐标原点在沙滩北个单位处,
若要使服务站到古村落和沙滩的距离相等,服务站需向左平移个单位即可.
故选:.
9.【答案】
【解析】,,
,
∽,
,
的距离为,动力臂,阻力臂,
,
,
的长为.
故选:.
10.【答案】
【解析】由题意得:从白鹭广场出发,匀速徒步至巴溪洲广场的速度为千米小时,
休整后再从巴溪洲广场匀速徒步至湘江保利时代的速度为千米小时,
当他徒步小时后含中途休整时间徒步的路程为千米,
他离终点目标的路程为千米.
故选:.
11.【答案】
【解析】分式有意义,
,
解得,,
故答案为:.
12.【答案】
【解析】两边都乘以,得
,
解得,
经检验是原方程的解,
所以原方程的解为.
故答案为:.
13.【答案】
【解析】设坡角为,已知一个山坡的坡度为:,
由题意得,,
.
故答案为:.
14.【答案】
【解析】一个不透明的布袋里装有个红球,个黄球,个白球,个黑球,
袋中球的总数为,
从袋中任意摸出个球,是黄球的概率为.
故答案为:.
15.【答案】
【解析】根据反比例函数系数的几何意义可知,,
即,
解得:;
函数图象位于第一、三象限,
,
故,
故答案为:.
16.【答案】
【解析】四边形是平行四边形,,
,
已知,
等边对等角,
即的度数为.
故答案为:.
17.【答案】原式
,
当时,
原式.
18.【答案】.
【解析】
.
19.【答案】,
,,
,
米,
在中,
,
米,
米.
答:米.
20.【答案】证明:如图,连接,
的垂直平分线交于点,
,
,
,
为中点,
;
,,
,
,
,
,
.
21.【答案】,,
,
是公共角,
只要作即可,
恰好,
作的角平分线即可.
如图所示:∽.
22.【解析】九年级班的学生人数人,
投中次的人数为:人,
扇形统计图中,
故答案为:;
,
故答案为:;
如下:
由图可知,共有种等可能的情况,其中恰好抽到名男生的情况有种,
,
概率是.
23.【解析】设购进种礼品盒的单价是元,种礼品盒的单价是元,
由题意得:,
解得:,
答:购进种礼品盒的单价是元,种礼品盒的单价是元;
设购进种礼品盒盒,则购进种礼品盒盒,
由题意得:,
解得:,
答:至少购进种礼品盒盒;
设销售利润为元,
由题意得:,
,
随的增大而减小,
当时,有最大值,最大值,
此时,,
答:购进种礼品盒盒,种礼品盒盒才能使销售利润最大,最大利润是元.
24.【解析】由题意知,,
,
,
,
;
证明:连接,
为的直径,
,
为过点的切线,
过点作的切线交于点,
,
,
,,
,
,
;
连接,
由可得,,,
,
设,,则,
,
,,
,
,
,,
::.
25.【答案】四边形是正方形,
,
将绕点旋转,使与重合,此时点的对应点在的延长线上,
,,
,
,
四边形为“直等补”四边形;
过作于点,如图,
则,
四边形是“直等补”四边形,,,,
,,
,
,
,
四边形是矩形,
,
,
,
,,
≌,
,
设,则,
,
,
解得,,或舍,
;
如图,延长到,使得,延长到,使得,连接,分别与、交于点、,过作,与的延长线交于点.
则,,
,
,,
的周长的值最小,
四边形是“直等补”四边形,
,
,
,
,
∽,
,
,,
,
,
,,
,
,
周长的最小值为.
第11页,共17页
同课章节目录
