2025年浙江省金华市东阳市九年级中考二模数学试卷(含解析)
文档属性
| 名称 | 2025年浙江省金华市东阳市九年级中考二模数学试卷(含解析) |  | |
| 格式 | docx | ||
| 文件大小 | 533.2KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 通用版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2025-05-29 17:26:48 | ||
图片预览




文档简介
2025年浙江省金华市东阳市九年级中考二模
数学试卷
一、选择题:本题共10小题,每小题3分,共30分。在每小题给出的选项中,只有一项是符合题目要求的。
1.的倒数是( )
A. B. C. D.
2.年,我市消费品以旧换新居家适老化改造申请户,完成改造户,完成系统审价补贴金额达元,数字用科学记数法表示为( )
A. B. C. D.
3.下列图标中,是中心对称图形的是( )
A. B. C. D.
4.下列运算结果正确的是( )
A. B. C. D.
5.某校名同学在歌唱比赛中的成绩单位:分分别为,,,,,这组数据的中位数是( )
A. B. C. D.
6.小聪在活动课上做“小孔成像”实验,如图所示,若,,蜡烛火焰倒立像,则下列说法中,错误的是( )
A. 蜡烛火焰和蜡烛火焰倒立像可以看成是位似图形
B.
C. 蜡烛火焰长
D. 线段中点与线段中点的连线不一定经过点
7.不等式组的解集在数轴上表示正确的是( )
A. B.
C. D.
8.如图是由个全等的直角三角形和一个小正方形组成的大正方形.若,,则直角的面积为( )
A. B. C. D.
9.已知反比例函数的图像上有,两点,下列说法正确的是( )
A. 当时, B. 当时,
C. 当时, D. 当时,
10.如图,是边长为的正三角形,点,分别是边,上的动点,连结,交于点,且作于点,于点下列两条线段的和,不随,的运动而改变的是( )
A. B. C. D.
二、填空题:本题共6小题,每小题3分,共18分。
11.分解因式: .
12.若一元二次方程有两个不相等的实数根,则的值可以是 写出一个即可.
13.如图,是的弦,与相切于点,经过圆心.若,则 .
14.不透明袋子中装有个球,其中有个红球、个绿球、个蓝球,这些球除颜色外无其他差别.从袋子中随机取出个球,则它是蓝球的概率是 .
15.如图,在中,垂直平分,点,分别是,的中点,连结,交于,延长交于点若,则的长为 .
16.如图,在中,为对角线上一点,且,线段与线段关于过点的直线对称,点的对应点在线段上,,与相交于点,连接,则四边形与的面积之比为 .
三、计算题:本大题共2小题,共12分。
17.计算:.
18.解方程组:.
四、解答题:本题共6小题,共60分。解答应写出文字说明,证明过程或演算步骤。
19.本小题分
如图,已知,,,在同一条直线上,,,,与交于点.
求证:.
若,,求的度数.
20.本小题分
如图,在中,,,.
利用直尺和圆规在上取一点,使得,保留作图痕迹.
求的面积.
21.本小题分
某校九年级学生共人,为了解九年级学生的体能情况,从中随机抽取部分学生进行分钟的跳绳测试,小慧将这次测试结果的数据分成组绘成如图所示频数直方图,并发现跳绳次数不少于次的同学占,第,两组频率之和为,且第组与第组的频数都是,第,,组频数之比为.
根据小慧提供的材料,请解答如下问题:
这次跳绳测试共抽取多少名学生?
第组的频数与频率分别是多少?
现学校计划表彰前的学生,请结合频数直方图确定被表彰学生的分钟跳绳次数,并说明理由.
22.本小题分
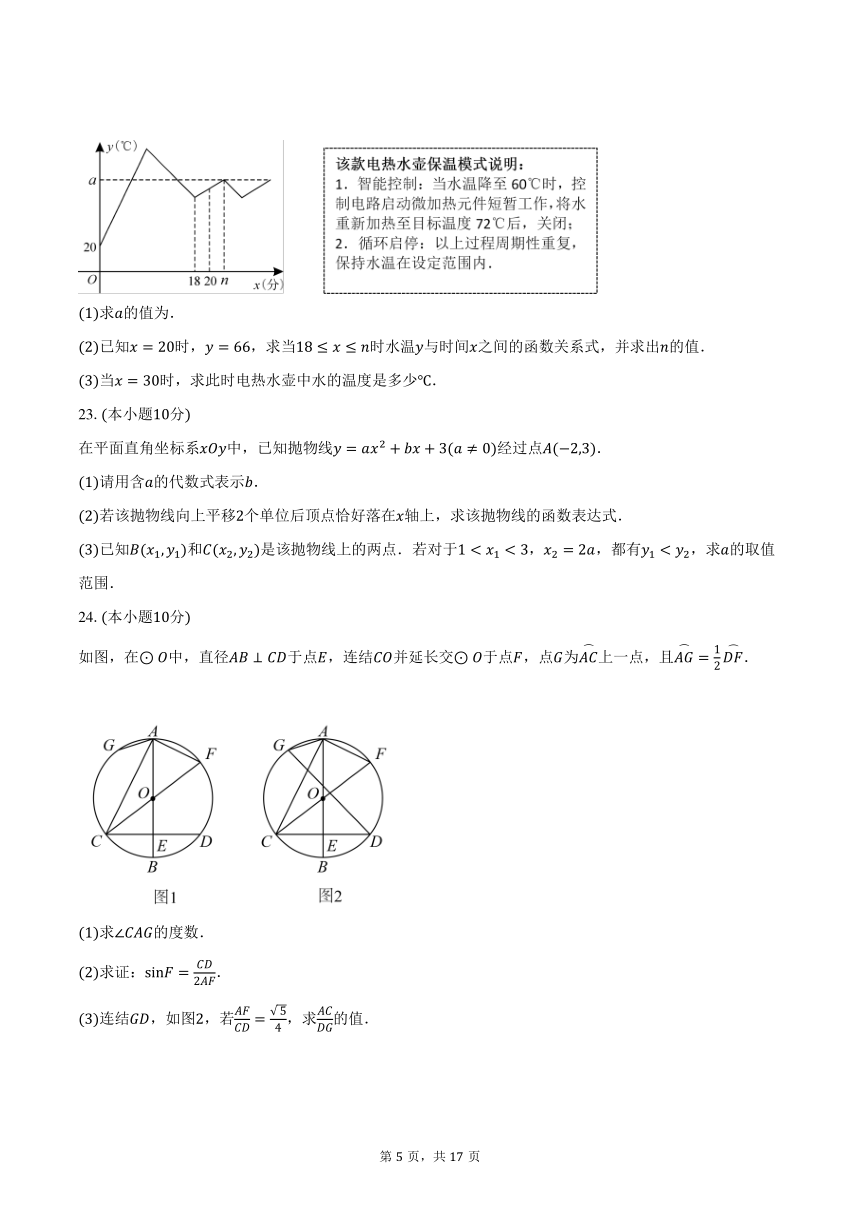
某款电热水壶有两种工作模式:煮沸模式和保温模式.在煮沸模式下将水加热后自动进入保温模式.现有一壶的水经过分钟烧至后进入保温模式,数学实验小组对这一过程进行了观察与记录,并绘制出水温与时间分的关系如图所示.
求的值为.
已知时,,求当时水温与时间之间的函数关系式,并求出的值.
当时,求此时电热水壶中水的温度是多少.
23.本小题分
在平面直角坐标系中,已知抛物线经过点.
请用含的代数式表示.
若该抛物线向上平移个单位后顶点恰好落在轴上,求该抛物线的函数表达式.
已知和是该抛物线上的两点.若对于,,都有,求的取值范围.
24.本小题分
如图,在中,直径于点,连结并延长交于点,点为上一点,且.
求的度数.
求证:.
连结,如图,若,求的值.
答案和解析
1.【答案】
【解析】的倒数是,故选:
2.【答案】
【解析】数字用科学记数法表示为.
故选:.
3.【答案】
【解析】选项A、、均不能找到这样的一个点,使图形绕某一点旋转后与原来的图形重合,所以不是中心对称图形;
选项C能找到这样的一个点,使图形绕某一点旋转后与原来的图形重合,所以是中心对称图形;
故选:.
4.【答案】
【解析】.,故该选项不正确,不符合题意;
B.和不是同类项,不能合并,故该选项不正确,不符合题意;;
C.,故该选项不正确,不符合题意;
D.,故该选项正确,符合题意;
故选:.
5.【答案】
【解析】从小到大重新排列为,,,,,最中间的那个数是
中位数是
故选:.
6.【答案】
【解析】由题意可得:,,
,
,
,故 B正确;
,故蜡烛火焰和蜡烛火焰倒立像可以看成是位似图形,故 A正确;
,
,即蜡烛火焰长,故 C正确;
线段中点与线段中点的连线一定经过点,故D错误,
故选:.
7.【答案】
【解析】由,得,
由,得,
不等式组的解集为.
在数轴上表示为:
故选:.
8.【答案】
【解析】设
依题意,,
直角的面积为,
故选:.
9.【答案】
【解析】当时,,反比例函数图象在第一、三象限,在每个象限内,随的增大而减小,
当时,在第三象限,在第一象限,
,,,故 B错误
当时,,,,都在第一象限,
则,故 A,C错误
当时,,
反比例函数图象在第二、四象限,在每个象限内,随的增大而增大,
在第二象限,在第四象限,
,,则,故 D选项正确
故选:.
10.【答案】
【解析】设,在中,,则,,证明得出,则,在中,根据得,进而由勾股定理得,则,据此即可得出答案.
【详解】解:设,
是等边三角形,且边长为,
,,
,,
和都是直角三角形,
在中,,
,,
是的外角,且,
,
,
,
在和中,
,
,
,
在中,,
,
,
,
的值不随、的运动而改变,始终是,
故选:.
11.【解析】,
故答案为:.
12.【答案】
【解析】一元二次方程有两个不相等的实数根,
,解得,
故答案为:答案不唯一.
13.【答案】
【解析】连接,
是的切线,
,
,
,
,
,
,
,
故答案为:.
14.【解析】袋子中装有个球,其中有个红球、个绿球和个蓝球,
从袋子中随机取出个球,它是蓝球的概率是:,
故答案为:.
15.【解析】垂直平分,
,且.
点是的中点,
,且,,
,
,
,
,
.
点是的中点,且,
,,,
,
,
,
,,
,
故答案为:.
16.【答案】
【解析】设直线与、相交于点、,连接,如图:
,
线段与线段关于过点的直线对称,点的对应点在线段上,
直线,、、三点共线,
,
设,则,,
,
,
,
设,则,
,
由对称性可得,,故,
,
,
,
,
与的对应高之比为,
的边上的高为,
,,
,,
四边形与的面积之比为,
故答案为:.
17.【解析】
18.【解析】
得,,
解得;,
将代入得,,
解得:,
方程组的解为:.
19. 【解析】证明:,
,
即,
,
,
在和中,
;
【小题】
解:由知,,
,
,
,
,
.
20. 【解析】如图,作的垂直平分线交于,点即为所求;
【小题】
解:过点作,垂足为,
,,
,,
,
,
,
设,则,
在中,,
,解得:
.
的面积.
21. 【解析】【小题】
跳绳次数不少于次的同学占,
第组占,
第,两组频率之和为,
第组的频率为:,
第组与第组的频数都是,
这次跳绳测试共抽取名学生;
【小题】
第,,组频数之比为,第组与第组的频数都是,
第组的频数为,
第组的频率为;
【小题】
第,,组频数之比为,
第组的频数为,
第组的频率为,
第组的频率为:,
第组和第组的频率之和为,
学校计划表彰前的学生,
被表彰学生的分钟跳绳次数是不少于次的学生.
22.【答案】【小题】
解:由图可见,水壶在保温模式下加热到的目标温度,即图中所示的水平线,即.
【小题】
解:设时水温随时间的函数为,当时,水温降至开始重新加热,已知时可得
,解得:
因此,时,.
当水温加热到时电路停止工作,故令得:
,解得.
答:当时,水温与时间之间的函数关系式,.
【小题】
解:从至为降温的分钟,每分钟降温,
从至为升温的分钟,
“从冷却到,需要分钟
再往后水壶会按“从冷却到,再加热回”的周期反复.可知每分钟完成一次“”的循环.
当时水温刚到,再经过分钟后即又回到.
故时,水温为.
23. 【解析】将代入得,
,
【小题】
,
抛物线解析式为
该抛物线向上平移个单位后顶点恰好落在轴上,即的顶点在轴上,
当时
抛物线解析式为
【小题】
抛物线为,点的横坐标,
对应.
对于,需满足:
即
分情况讨论:
当:需,最大值 时,解得.
当 :需,最小值 时,解得.
所以:的取值范围为 或.
24. 【解析】【小题】
如解图,连接、,
,
,
,
,
又,
,
,
,
,
,
【小题】如解图,连接,
,
,
,是直径,
,,
,
,
【小题】
连接、、、过点作,垂足为,
由可知:,
,
,
设,则,
,,
是直径,
,
,即,
,
,
,
由得,,
又,,
,
,,
,
,
.
第1页,共17页
数学试卷
一、选择题:本题共10小题,每小题3分,共30分。在每小题给出的选项中,只有一项是符合题目要求的。
1.的倒数是( )
A. B. C. D.
2.年,我市消费品以旧换新居家适老化改造申请户,完成改造户,完成系统审价补贴金额达元,数字用科学记数法表示为( )
A. B. C. D.
3.下列图标中,是中心对称图形的是( )
A. B. C. D.
4.下列运算结果正确的是( )
A. B. C. D.
5.某校名同学在歌唱比赛中的成绩单位:分分别为,,,,,这组数据的中位数是( )
A. B. C. D.
6.小聪在活动课上做“小孔成像”实验,如图所示,若,,蜡烛火焰倒立像,则下列说法中,错误的是( )
A. 蜡烛火焰和蜡烛火焰倒立像可以看成是位似图形
B.
C. 蜡烛火焰长
D. 线段中点与线段中点的连线不一定经过点
7.不等式组的解集在数轴上表示正确的是( )
A. B.
C. D.
8.如图是由个全等的直角三角形和一个小正方形组成的大正方形.若,,则直角的面积为( )
A. B. C. D.
9.已知反比例函数的图像上有,两点,下列说法正确的是( )
A. 当时, B. 当时,
C. 当时, D. 当时,
10.如图,是边长为的正三角形,点,分别是边,上的动点,连结,交于点,且作于点,于点下列两条线段的和,不随,的运动而改变的是( )
A. B. C. D.
二、填空题:本题共6小题,每小题3分,共18分。
11.分解因式: .
12.若一元二次方程有两个不相等的实数根,则的值可以是 写出一个即可.
13.如图,是的弦,与相切于点,经过圆心.若,则 .
14.不透明袋子中装有个球,其中有个红球、个绿球、个蓝球,这些球除颜色外无其他差别.从袋子中随机取出个球,则它是蓝球的概率是 .
15.如图,在中,垂直平分,点,分别是,的中点,连结,交于,延长交于点若,则的长为 .
16.如图,在中,为对角线上一点,且,线段与线段关于过点的直线对称,点的对应点在线段上,,与相交于点,连接,则四边形与的面积之比为 .
三、计算题:本大题共2小题,共12分。
17.计算:.
18.解方程组:.
四、解答题:本题共6小题,共60分。解答应写出文字说明,证明过程或演算步骤。
19.本小题分
如图,已知,,,在同一条直线上,,,,与交于点.
求证:.
若,,求的度数.
20.本小题分
如图,在中,,,.
利用直尺和圆规在上取一点,使得,保留作图痕迹.
求的面积.
21.本小题分
某校九年级学生共人,为了解九年级学生的体能情况,从中随机抽取部分学生进行分钟的跳绳测试,小慧将这次测试结果的数据分成组绘成如图所示频数直方图,并发现跳绳次数不少于次的同学占,第,两组频率之和为,且第组与第组的频数都是,第,,组频数之比为.
根据小慧提供的材料,请解答如下问题:
这次跳绳测试共抽取多少名学生?
第组的频数与频率分别是多少?
现学校计划表彰前的学生,请结合频数直方图确定被表彰学生的分钟跳绳次数,并说明理由.
22.本小题分
某款电热水壶有两种工作模式:煮沸模式和保温模式.在煮沸模式下将水加热后自动进入保温模式.现有一壶的水经过分钟烧至后进入保温模式,数学实验小组对这一过程进行了观察与记录,并绘制出水温与时间分的关系如图所示.
求的值为.
已知时,,求当时水温与时间之间的函数关系式,并求出的值.
当时,求此时电热水壶中水的温度是多少.
23.本小题分
在平面直角坐标系中,已知抛物线经过点.
请用含的代数式表示.
若该抛物线向上平移个单位后顶点恰好落在轴上,求该抛物线的函数表达式.
已知和是该抛物线上的两点.若对于,,都有,求的取值范围.
24.本小题分
如图,在中,直径于点,连结并延长交于点,点为上一点,且.
求的度数.
求证:.
连结,如图,若,求的值.
答案和解析
1.【答案】
【解析】的倒数是,故选:
2.【答案】
【解析】数字用科学记数法表示为.
故选:.
3.【答案】
【解析】选项A、、均不能找到这样的一个点,使图形绕某一点旋转后与原来的图形重合,所以不是中心对称图形;
选项C能找到这样的一个点,使图形绕某一点旋转后与原来的图形重合,所以是中心对称图形;
故选:.
4.【答案】
【解析】.,故该选项不正确,不符合题意;
B.和不是同类项,不能合并,故该选项不正确,不符合题意;;
C.,故该选项不正确,不符合题意;
D.,故该选项正确,符合题意;
故选:.
5.【答案】
【解析】从小到大重新排列为,,,,,最中间的那个数是
中位数是
故选:.
6.【答案】
【解析】由题意可得:,,
,
,
,故 B正确;
,故蜡烛火焰和蜡烛火焰倒立像可以看成是位似图形,故 A正确;
,
,即蜡烛火焰长,故 C正确;
线段中点与线段中点的连线一定经过点,故D错误,
故选:.
7.【答案】
【解析】由,得,
由,得,
不等式组的解集为.
在数轴上表示为:
故选:.
8.【答案】
【解析】设
依题意,,
直角的面积为,
故选:.
9.【答案】
【解析】当时,,反比例函数图象在第一、三象限,在每个象限内,随的增大而减小,
当时,在第三象限,在第一象限,
,,,故 B错误
当时,,,,都在第一象限,
则,故 A,C错误
当时,,
反比例函数图象在第二、四象限,在每个象限内,随的增大而增大,
在第二象限,在第四象限,
,,则,故 D选项正确
故选:.
10.【答案】
【解析】设,在中,,则,,证明得出,则,在中,根据得,进而由勾股定理得,则,据此即可得出答案.
【详解】解:设,
是等边三角形,且边长为,
,,
,,
和都是直角三角形,
在中,,
,,
是的外角,且,
,
,
,
在和中,
,
,
,
在中,,
,
,
,
的值不随、的运动而改变,始终是,
故选:.
11.【解析】,
故答案为:.
12.【答案】
【解析】一元二次方程有两个不相等的实数根,
,解得,
故答案为:答案不唯一.
13.【答案】
【解析】连接,
是的切线,
,
,
,
,
,
,
,
故答案为:.
14.【解析】袋子中装有个球,其中有个红球、个绿球和个蓝球,
从袋子中随机取出个球,它是蓝球的概率是:,
故答案为:.
15.【解析】垂直平分,
,且.
点是的中点,
,且,,
,
,
,
,
.
点是的中点,且,
,,,
,
,
,
,,
,
故答案为:.
16.【答案】
【解析】设直线与、相交于点、,连接,如图:
,
线段与线段关于过点的直线对称,点的对应点在线段上,
直线,、、三点共线,
,
设,则,,
,
,
,
设,则,
,
由对称性可得,,故,
,
,
,
,
与的对应高之比为,
的边上的高为,
,,
,,
四边形与的面积之比为,
故答案为:.
17.【解析】
18.【解析】
得,,
解得;,
将代入得,,
解得:,
方程组的解为:.
19. 【解析】证明:,
,
即,
,
,
在和中,
;
【小题】
解:由知,,
,
,
,
,
.
20. 【解析】如图,作的垂直平分线交于,点即为所求;
【小题】
解:过点作,垂足为,
,,
,,
,
,
,
设,则,
在中,,
,解得:
.
的面积.
21. 【解析】【小题】
跳绳次数不少于次的同学占,
第组占,
第,两组频率之和为,
第组的频率为:,
第组与第组的频数都是,
这次跳绳测试共抽取名学生;
【小题】
第,,组频数之比为,第组与第组的频数都是,
第组的频数为,
第组的频率为;
【小题】
第,,组频数之比为,
第组的频数为,
第组的频率为,
第组的频率为:,
第组和第组的频率之和为,
学校计划表彰前的学生,
被表彰学生的分钟跳绳次数是不少于次的学生.
22.【答案】【小题】
解:由图可见,水壶在保温模式下加热到的目标温度,即图中所示的水平线,即.
【小题】
解:设时水温随时间的函数为,当时,水温降至开始重新加热,已知时可得
,解得:
因此,时,.
当水温加热到时电路停止工作,故令得:
,解得.
答:当时,水温与时间之间的函数关系式,.
【小题】
解:从至为降温的分钟,每分钟降温,
从至为升温的分钟,
“从冷却到,需要分钟
再往后水壶会按“从冷却到,再加热回”的周期反复.可知每分钟完成一次“”的循环.
当时水温刚到,再经过分钟后即又回到.
故时,水温为.
23. 【解析】将代入得,
,
【小题】
,
抛物线解析式为
该抛物线向上平移个单位后顶点恰好落在轴上,即的顶点在轴上,
当时
抛物线解析式为
【小题】
抛物线为,点的横坐标,
对应.
对于,需满足:
即
分情况讨论:
当:需,最大值 时,解得.
当 :需,最小值 时,解得.
所以:的取值范围为 或.
24. 【解析】【小题】
如解图,连接、,
,
,
,
,
又,
,
,
,
,
,
【小题】如解图,连接,
,
,
,是直径,
,,
,
,
【小题】
连接、、、过点作,垂足为,
由可知:,
,
,
设,则,
,,
是直径,
,
,即,
,
,
,
由得,,
又,,
,
,,
,
,
.
第1页,共17页
同课章节目录
