中考数学复习微专题三旋转问题课件(共18张PPT)
文档属性
| 名称 | 中考数学复习微专题三旋转问题课件(共18张PPT) |  | |
| 格式 | ppt | ||
| 文件大小 | 13.2MB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 通用版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2025-05-31 09:16:22 | ||
图片预览





文档简介
(共18张PPT)
微专题三 旋 转 问 题
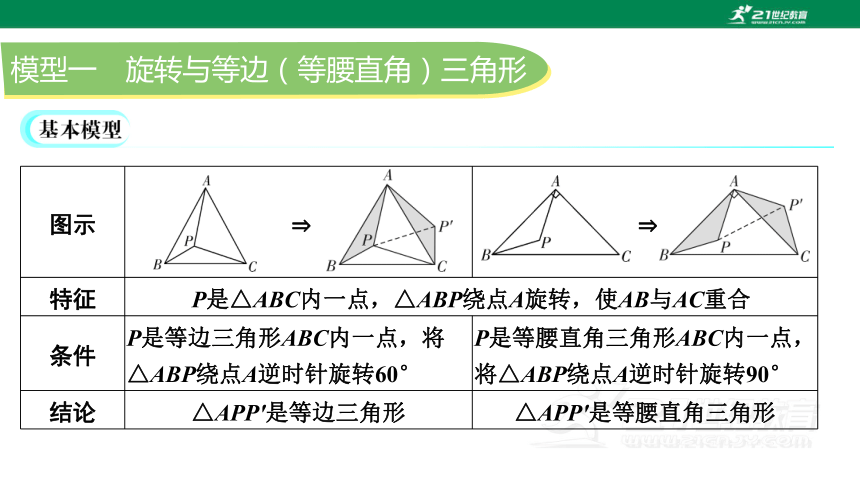
模型一 旋转与等边(等腰直角)三角形
图示
特征 P是△ABC内一点,△ABP绕点A旋转,使AB与AC重合
条件 P是等边三角形ABC内一点,将△ABP绕点A逆时针旋转60° P是等腰直角三角形ABC内一点,将△ABP绕点A逆时针旋转90°
结论 △APP'是等边三角形 △APP'是等腰直角三角形
图W-3-1
答图W-3-1
例2. (教材改编)如图W-3-2,等腰直角三角形ABC内有一点P,连接AP,BP,CP,∠APB=135°,将△ABP绕点A逆时针旋转90°得到△ACP',连接PP'. 判断AP,BP,CP三条线段的数量关系,并说明理由.
图W-3-2
解:CP2=BP2+2AP2.
理由如下:
由旋转的性质,得AP'=AP,∠PAP'=∠BAC=90°,CP'=BP,∠AP'C=∠APB=135°.
∴△APP'是等腰直角三角形.
∴∠APP'=∠AP'P=45°,PP'2=AP2+AP'2=2AP2.
∴∠PP'C=∠AP'C-∠AP'P=90°. ∴△CPP'是直角三角形.
∴CP2=CP'2+PP'2=BP2+2AP2.
1. 如图W-3-3,在等边三角形ABC中,P为△ABC内一点,连接AP,BP,CP,将线段AP绕点A顺时针旋转60°得到AP',连接PP',BP'.
(1)用等式表示BP'与CP的数量关系,并证明;
图W-3-3
解:(1)BP'=CP.
证明如下:∵△ABC是等边三角形,
∴AB=AC,∠BAC=60°. ∴∠BAP+∠CAP=60°.
∵将线段AP绕点A顺时针旋转60°得到AP',
∴AP'=AP,∠PAP'=60°. ∴∠BAP'+∠BAP=60°. ∴∠BAP'=∠CAP.
∴△ABP'≌△ACP(SAS). ∴BP'=CP.
(2)当∠BPC=120°时,求∠P'BP的度数.
(2)当∠BPC=120°时,则∠CBP+∠BCP=
180°-∠BPC=60°.
∵△ABP'≌△ACP,∴∠ABP'=∠ACP.
∴∠P'BP=∠ABP'+∠ABP=∠ACP+∠ABP=
60°-∠BCP+60°-∠CBP=120°-(∠CBP+
∠BCP)=60°.
图W-3-3
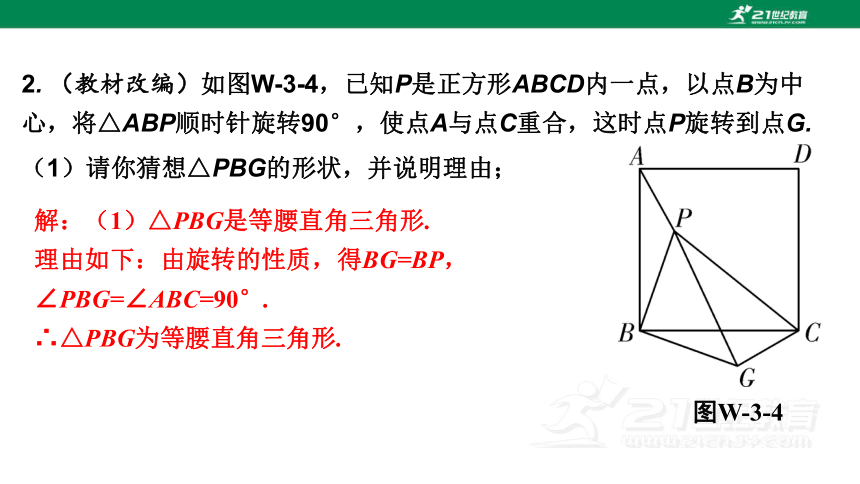
2. (教材改编)如图W-3-4,已知P是正方形ABCD内一点,以点B为中心,将△ABP顺时针旋转90°,使点A与点C重合,这时点P旋转到点G.
(1)请你猜想△PBG的形状,并说明理由;
图W-3-4
解:(1)△PBG是等腰直角三角形.
理由如下:由旋转的性质,得BG=BP,∠PBG=∠ABC=90°.
∴△PBG为等腰直角三角形.
图W-3-4
模型二 旋转中的半角模型
常见模型 正方形中的半角模型 等腰直角三角形中的半角模型
图示
常见模型 正方形中的半角模型 等腰直角三角形中的半角模型
特征 △ADF绕点A顺时针
旋转90°得到△ABG
构造△ABG≌△ADF △ABE绕点A逆时针
旋转90°得到△ADG
构造△ADG≌△ABE △ACE绕点A顺时针
旋转90°得到△ABF
构造△ABF≌△ACE △ABD绕点A逆时针
旋转90°得到△ACF
构造△ACF≌△ABD
常见模型 正方形中的半角模型 等腰直角三角形中的半角模型
条件 在正方形ABCD中,
∠EAF=45° 在正方形ABCD中,
∠EAF=45° 在等腰直角三角形ABC
中,∠BAC=90°,
∠DAE=45° 在等腰直角三角形ABC
中,∠BAC=90°,
∠DAE=45°
结论 EF=BE+DF EF=DF-BE BD2 +CE2=DE2 BD2 +CE2=DE2
例3. (教材改编)如图W-3-5,在正方形ABCD中,E,F分别是BC,CD边上的动点,且∠EAF=45°.
(1)求证:EF=DF+BE;
图W-3-5
答图W-3-3
图W-3-5
3. (教材改编)在正方形ABCD中,E,F分别是BC,CD边所在直线上的动点,且∠EAF=45°.
(1)如图W-3-6①,如果E,F分别是射线CB,DC上的动点,且∠EAF=45°,请写出EF,BE,DF之间的数量关系并证明;
图W-3-6
答图W-3-4
(2)如图W-3-6②,如果E,F分别是射线BC,CD上的动点,且∠EAF=45°,则EF,BE,DF之间的数量关系是 . (不要求证明)
EF=BE-DF
图W-3-6
4. 如图W-3-7,已知等腰直角三角形ABC,∠BAC=90°,点D,E在边BC上(点D在点E左侧),且∠DAE=45°. 求证:(1)△ABE∽△DAE;
证明:(1)∵∠BAC=90°,AB=AC,
∴∠B=∠C=45°.
∴∠DAE=∠ABE.
又∵∠AEB=∠DEA,∴△ABE∽△DAE.
图W-3-7
(2)DE2=BD2+EC2.
答图W-3-5
微专题三 旋 转 问 题
模型一 旋转与等边(等腰直角)三角形
图示
特征 P是△ABC内一点,△ABP绕点A旋转,使AB与AC重合
条件 P是等边三角形ABC内一点,将△ABP绕点A逆时针旋转60° P是等腰直角三角形ABC内一点,将△ABP绕点A逆时针旋转90°
结论 △APP'是等边三角形 △APP'是等腰直角三角形
图W-3-1
答图W-3-1
例2. (教材改编)如图W-3-2,等腰直角三角形ABC内有一点P,连接AP,BP,CP,∠APB=135°,将△ABP绕点A逆时针旋转90°得到△ACP',连接PP'. 判断AP,BP,CP三条线段的数量关系,并说明理由.
图W-3-2
解:CP2=BP2+2AP2.
理由如下:
由旋转的性质,得AP'=AP,∠PAP'=∠BAC=90°,CP'=BP,∠AP'C=∠APB=135°.
∴△APP'是等腰直角三角形.
∴∠APP'=∠AP'P=45°,PP'2=AP2+AP'2=2AP2.
∴∠PP'C=∠AP'C-∠AP'P=90°. ∴△CPP'是直角三角形.
∴CP2=CP'2+PP'2=BP2+2AP2.
1. 如图W-3-3,在等边三角形ABC中,P为△ABC内一点,连接AP,BP,CP,将线段AP绕点A顺时针旋转60°得到AP',连接PP',BP'.
(1)用等式表示BP'与CP的数量关系,并证明;
图W-3-3
解:(1)BP'=CP.
证明如下:∵△ABC是等边三角形,
∴AB=AC,∠BAC=60°. ∴∠BAP+∠CAP=60°.
∵将线段AP绕点A顺时针旋转60°得到AP',
∴AP'=AP,∠PAP'=60°. ∴∠BAP'+∠BAP=60°. ∴∠BAP'=∠CAP.
∴△ABP'≌△ACP(SAS). ∴BP'=CP.
(2)当∠BPC=120°时,求∠P'BP的度数.
(2)当∠BPC=120°时,则∠CBP+∠BCP=
180°-∠BPC=60°.
∵△ABP'≌△ACP,∴∠ABP'=∠ACP.
∴∠P'BP=∠ABP'+∠ABP=∠ACP+∠ABP=
60°-∠BCP+60°-∠CBP=120°-(∠CBP+
∠BCP)=60°.
图W-3-3
2. (教材改编)如图W-3-4,已知P是正方形ABCD内一点,以点B为中心,将△ABP顺时针旋转90°,使点A与点C重合,这时点P旋转到点G.
(1)请你猜想△PBG的形状,并说明理由;
图W-3-4
解:(1)△PBG是等腰直角三角形.
理由如下:由旋转的性质,得BG=BP,∠PBG=∠ABC=90°.
∴△PBG为等腰直角三角形.
图W-3-4
模型二 旋转中的半角模型
常见模型 正方形中的半角模型 等腰直角三角形中的半角模型
图示
常见模型 正方形中的半角模型 等腰直角三角形中的半角模型
特征 △ADF绕点A顺时针
旋转90°得到△ABG
构造△ABG≌△ADF △ABE绕点A逆时针
旋转90°得到△ADG
构造△ADG≌△ABE △ACE绕点A顺时针
旋转90°得到△ABF
构造△ABF≌△ACE △ABD绕点A逆时针
旋转90°得到△ACF
构造△ACF≌△ABD
常见模型 正方形中的半角模型 等腰直角三角形中的半角模型
条件 在正方形ABCD中,
∠EAF=45° 在正方形ABCD中,
∠EAF=45° 在等腰直角三角形ABC
中,∠BAC=90°,
∠DAE=45° 在等腰直角三角形ABC
中,∠BAC=90°,
∠DAE=45°
结论 EF=BE+DF EF=DF-BE BD2 +CE2=DE2 BD2 +CE2=DE2
例3. (教材改编)如图W-3-5,在正方形ABCD中,E,F分别是BC,CD边上的动点,且∠EAF=45°.
(1)求证:EF=DF+BE;
图W-3-5
答图W-3-3
图W-3-5
3. (教材改编)在正方形ABCD中,E,F分别是BC,CD边所在直线上的动点,且∠EAF=45°.
(1)如图W-3-6①,如果E,F分别是射线CB,DC上的动点,且∠EAF=45°,请写出EF,BE,DF之间的数量关系并证明;
图W-3-6
答图W-3-4
(2)如图W-3-6②,如果E,F分别是射线BC,CD上的动点,且∠EAF=45°,则EF,BE,DF之间的数量关系是 . (不要求证明)
EF=BE-DF
图W-3-6
4. 如图W-3-7,已知等腰直角三角形ABC,∠BAC=90°,点D,E在边BC上(点D在点E左侧),且∠DAE=45°. 求证:(1)△ABE∽△DAE;
证明:(1)∵∠BAC=90°,AB=AC,
∴∠B=∠C=45°.
∴∠DAE=∠ABE.
又∵∠AEB=∠DEA,∴△ABE∽△DAE.
图W-3-7
(2)DE2=BD2+EC2.
答图W-3-5
同课章节目录
