中考数学复习微专题七代数最值问题课件(共15张PPT)
文档属性
| 名称 | 中考数学复习微专题七代数最值问题课件(共15张PPT) |  | |
| 格式 | ppt | ||
| 文件大小 | 13.3MB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 通用版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2025-05-31 09:16:06 | ||
图片预览





文档简介
(共15张PPT)
微专题七 代数最值问题
知识解读
在中考数学中,建立函数模型并求最值是一个常见的题型.解决这类问题的方法如下:
1. 理解题意:仔细阅读题目,理解问题的背景和要求,确定题目中给出的已知条件和未知量.
2. 建立函数模型:根据题目的描述,尝试找到一个或多个变量之间的关系式. 这个关系式通常可以表示为一个函数,其中自变量和因变量要明确.
3. 确定函数的自变量取值范围:考虑到实际问题的背景,确定函数自变量的范围.
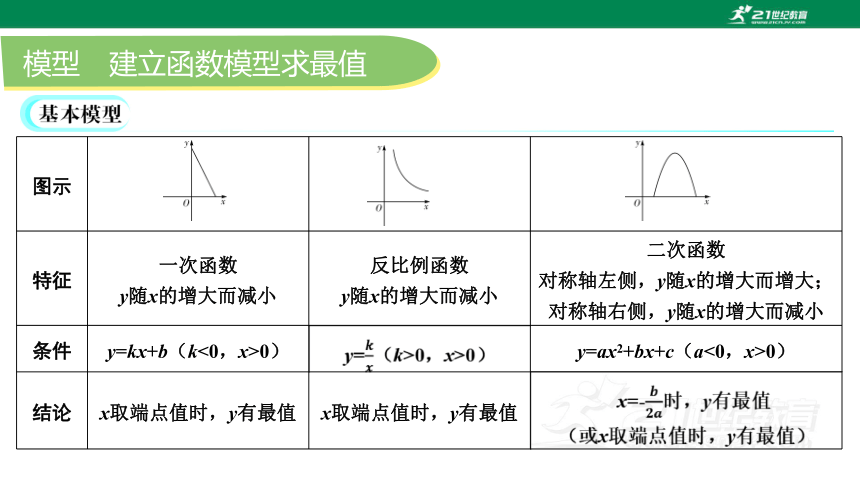
模型 建立函数模型求最值
图示
特征 一次函数
y随x的增大而减小 反比例函数
y随x的增大而减小 二次函数
对称轴左侧,y随x的增大而增大;
对称轴右侧,y随x的增大而减小
条件 y=kx+b(k<0,x>0) y=ax2+bx+c(a<0,x>0)
结论 x取端点值时,y有最值 x取端点值时,y有最值
例1. (2024·广安)某小区物管中心计划采购A,B两种花卉用于美化环境. 已知购买2株A种花卉和3株B种花卉共需要21元;购买4株A种花卉和5株B种花卉共需要37元.
(1)求A,B两种花卉的单价;
(2)该物管中心计划采购A,B两种花卉共计10 000株,其中采购A种花卉的株数不超过B种花卉株数的4倍,当A,B两种花卉分别采购多少株时,总费用最少?并求出最少总费用.
(2)设采购A种花卉m株,则B种花卉(10 000-m)株,总费用为W元.
由题意,得W=3m+5(10 000-m)=-2m+50 000.
∵m≤4(10 000-m),解得m≤8 000.
在W=-2m+50 000中,∵-2<0,∴W随m的增大而减小.
∴当m=8 000时,W取得最小值,W最小=-2×8 000+50 000=34 000. 此时 10 000-m=2 000.
答:当购进A种花卉8 000株,B种花卉2 000株时,总费用最少,最少总费用为34 000元.
图W-7-1
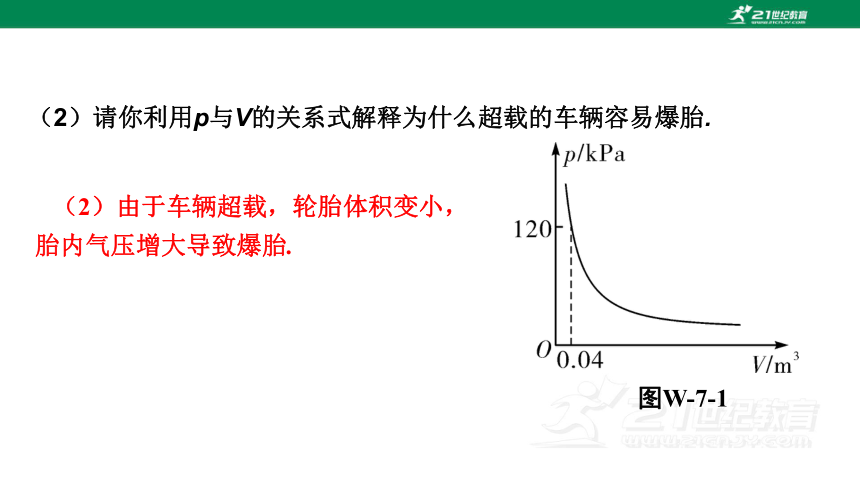
(2)请你利用p与V的关系式解释为什么超载的车辆容易爆胎.
图W-7-1
(2)由于车辆超载,轮胎体积变小,胎内气压增大导致爆胎.
图W-7-2
(2)当成本最低时,销售产品所获利润是多少?
图W-7-2
(3)当销售量是多少吨时,可获得最大利润?最大利润是多少?
(注:利润=销售额-成本)
图W-7-2
1. (2024·眉山)眉山是“三苏”故里,文化底蕴深厚. 近年来眉山市旅游产业蓬勃发展,促进了文创产品的销售,某商店用960元购进的A款文创产品和用780元购进的B款文创产品数量相同. 每件A款文创产品进价比B款文创产品进价多15元.
(1)A,B两款文创产品每件的进价各是多少元?
(2)已知A款文创产品每件售价为100元,B款文创产品每件售价为80元,根据市场需求,商店计划再用不超过7 400元的总费用购进这两款文创产品共100件进行销售,问:怎样进货才能使销售完后获得的利润最大?最大利润是多少元?
(2)设购进A款文创产品x件,则购进B款文创产品(100-x)件,总利润为w元.
由题意,得80x+65(100-x)≤7 400. 解得x≤60.
∴w=(100-80)x+(80-65)(100-x)=5x+1 500.
∵k=5>0,∴w随x的增大而增大.
∴当x=60时,w取得最大值,w最大=5×60+1 500=1 800. 此时100-x=40.
答:购进A款文创产品60件,B款文创产品40件,才能使销售完后获得的利润最大,最大利润是1 800元.
2. (2024·济宁)某商场以每件80元的价格购进一种商品,在一段时间内,销售量y(件)与销售单价x(元/件)之间是一次函数关系,其部分图象如图W-7-3所示.
(1)求这段时间内y与x之间的函数解析式;
图W-7-3
(2)在这段时间内,若销售单价不低于100元,且商场还要完成不少于220件的销售任务,当销售单价为多少时,商场获得利润最大?最大利润是多少?
图W-7-3
微专题七 代数最值问题
知识解读
在中考数学中,建立函数模型并求最值是一个常见的题型.解决这类问题的方法如下:
1. 理解题意:仔细阅读题目,理解问题的背景和要求,确定题目中给出的已知条件和未知量.
2. 建立函数模型:根据题目的描述,尝试找到一个或多个变量之间的关系式. 这个关系式通常可以表示为一个函数,其中自变量和因变量要明确.
3. 确定函数的自变量取值范围:考虑到实际问题的背景,确定函数自变量的范围.
模型 建立函数模型求最值
图示
特征 一次函数
y随x的增大而减小 反比例函数
y随x的增大而减小 二次函数
对称轴左侧,y随x的增大而增大;
对称轴右侧,y随x的增大而减小
条件 y=kx+b(k<0,x>0) y=ax2+bx+c(a<0,x>0)
结论 x取端点值时,y有最值 x取端点值时,y有最值
例1. (2024·广安)某小区物管中心计划采购A,B两种花卉用于美化环境. 已知购买2株A种花卉和3株B种花卉共需要21元;购买4株A种花卉和5株B种花卉共需要37元.
(1)求A,B两种花卉的单价;
(2)该物管中心计划采购A,B两种花卉共计10 000株,其中采购A种花卉的株数不超过B种花卉株数的4倍,当A,B两种花卉分别采购多少株时,总费用最少?并求出最少总费用.
(2)设采购A种花卉m株,则B种花卉(10 000-m)株,总费用为W元.
由题意,得W=3m+5(10 000-m)=-2m+50 000.
∵m≤4(10 000-m),解得m≤8 000.
在W=-2m+50 000中,∵-2<0,∴W随m的增大而减小.
∴当m=8 000时,W取得最小值,W最小=-2×8 000+50 000=34 000. 此时 10 000-m=2 000.
答:当购进A种花卉8 000株,B种花卉2 000株时,总费用最少,最少总费用为34 000元.
图W-7-1
(2)请你利用p与V的关系式解释为什么超载的车辆容易爆胎.
图W-7-1
(2)由于车辆超载,轮胎体积变小,胎内气压增大导致爆胎.
图W-7-2
(2)当成本最低时,销售产品所获利润是多少?
图W-7-2
(3)当销售量是多少吨时,可获得最大利润?最大利润是多少?
(注:利润=销售额-成本)
图W-7-2
1. (2024·眉山)眉山是“三苏”故里,文化底蕴深厚. 近年来眉山市旅游产业蓬勃发展,促进了文创产品的销售,某商店用960元购进的A款文创产品和用780元购进的B款文创产品数量相同. 每件A款文创产品进价比B款文创产品进价多15元.
(1)A,B两款文创产品每件的进价各是多少元?
(2)已知A款文创产品每件售价为100元,B款文创产品每件售价为80元,根据市场需求,商店计划再用不超过7 400元的总费用购进这两款文创产品共100件进行销售,问:怎样进货才能使销售完后获得的利润最大?最大利润是多少元?
(2)设购进A款文创产品x件,则购进B款文创产品(100-x)件,总利润为w元.
由题意,得80x+65(100-x)≤7 400. 解得x≤60.
∴w=(100-80)x+(80-65)(100-x)=5x+1 500.
∵k=5>0,∴w随x的增大而增大.
∴当x=60时,w取得最大值,w最大=5×60+1 500=1 800. 此时100-x=40.
答:购进A款文创产品60件,B款文创产品40件,才能使销售完后获得的利润最大,最大利润是1 800元.
2. (2024·济宁)某商场以每件80元的价格购进一种商品,在一段时间内,销售量y(件)与销售单价x(元/件)之间是一次函数关系,其部分图象如图W-7-3所示.
(1)求这段时间内y与x之间的函数解析式;
图W-7-3
(2)在这段时间内,若销售单价不低于100元,且商场还要完成不少于220件的销售任务,当销售单价为多少时,商场获得利润最大?最大利润是多少?
图W-7-3
同课章节目录
