中考数学复习选填题突破常用方法课件(共21张PPT)
文档属性
| 名称 | 中考数学复习选填题突破常用方法课件(共21张PPT) |  | |
| 格式 | ppt | ||
| 文件大小 | 2.9MB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 通用版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2025-05-31 09:18:09 | ||
图片预览







文档简介
(共21张PPT)
选填题常用方法
第十章 选填题突破
选填题常用方法
选择题和填空题都具有构思巧妙、概念性强、知识容量大、覆盖面广且评分标准统一等优点,因而历来是中考数学的重要题型,要想迅速、正确地解题,除了要有准确的计算、严密的推理外,还必须掌握其解题方法与技巧,下面介绍选填的几种常用方法.
1 直接法
直接从题目条件出发,运用相关的性质、定理、法则、公式等,通过准确运算、严密推理和合理验证,最后得出正确的结果,运用此方法解题需要扎实的数学基础.
例1. (2024·南通)如果零上2 ℃记作+2 ℃,那么零下3 ℃记作 ( )
A. -3 ℃ B. 3 ℃ C. -5 ℃ D. 5 ℃
例2. (2024·福建)因式分解:x2+x= .
A
x(x+1)
2 检验法
将选项分别代入题设中或将题设代入选项中检验,然后选择符合题设条件的选项的一种方法.当结论为具体值时可考虑使用检验法,在运用检验法时,若能根据题意确定代入顺序,则更能提高解题速度,反之会造成计算和推理量过大.
D
(答案不唯一)
3 排除筛选法
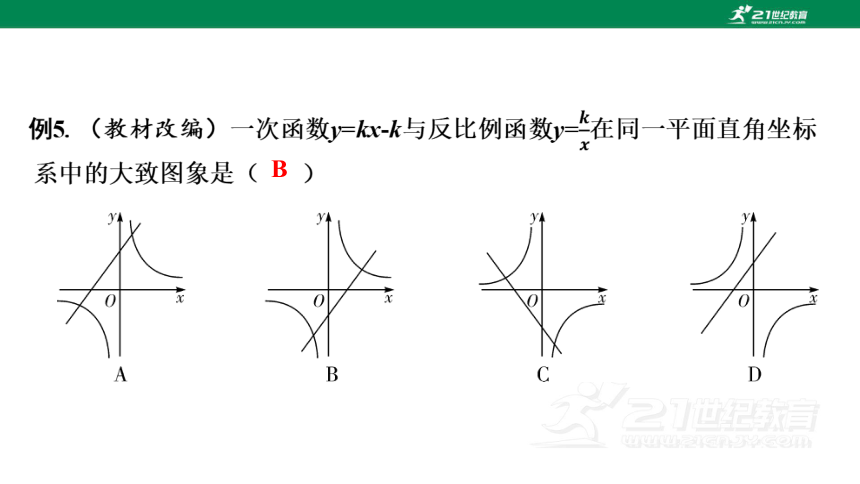
对于正确答案只有一个的选择题,根据题设条件和有关知识,通过分析、推理、演算等,筛除一些较易判定的、不合题意的结论,缩小选择的范围,再从其余结论中求得正确答案.这种方法适用于定性或不易求解的选择题,它与特殊值法、数形结合法等结合使用是选择题的常规方法.
B
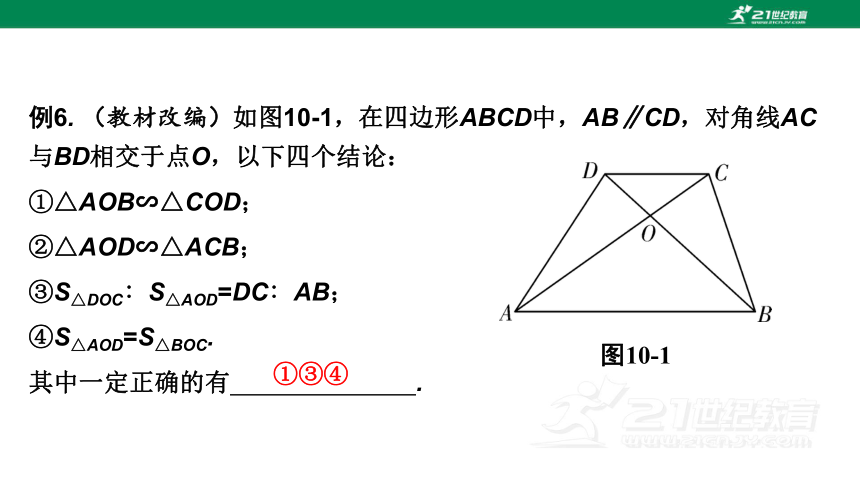
例6. (教材改编)如图10-1,在四边形ABCD中,AB∥CD,对角线AC与BD相交于点O,以下四个结论:
①△AOB∽△COD;
②△AOD∽△ACB;
③S△DOC∶S△AOD=DC∶AB;
④S△AOD=S△BOC.
其中一定正确的有 .
图10-1
①③④
4 特殊值法
根据题设情况,选取满足条件的特殊数值、特殊的点、特殊的图形或特殊的位置状态,代替题设的普遍条件,将一般形式转化为特殊形式进行求解的方法.
例7. (教材改编)已知x+y+z=0,则(x+y)(y+z)(z+x)+xyz的值为 ( )
A. 1 B. 0 C. 3 D. -1
B
例8. (教材改编)如图10-2,矩形ABCD的面积为1,E,F,G,H分别为四条边的中点,I是FE上任一动点,则阴影部分的面积为 .
图10-2
5 整体代入法
把某个式子看作一个整体代入原有的问题中,从而简化问题得到答案的一种方法.在求多项式的值的问题中,若字母的取值不知道或不易求出,即可采用该方法巧妙求出多项式的值.
例9. (2023·常德)若a2+3a-4=0,则2a2+6a-3= ( )
A. 5 B. 1 C. -1 D. 0
例10. (2024·苏州)若a=b+2,则(b-a)2= .
A
4
6 数形结合法
数形结合法是利用函数图象或某些特殊值的几何意义,将代数的问题(如解方程、解不等式、求最值、求取值范围等)与几何图形相结合,数与形相互转化,使问题化繁为简,从而确定正确答案的方法.
图10-3
A
图10-4
B
7 等价转化法
通过观察、分析、类比、联想等,借助某些性质、公式或已知条件,选择恰当的数学方法将某些问题进行转化,由复杂转化为简单,由未知转化为已知,由抽象转化为具体,从而进行计算.
例13. (教材改编)边长相等的两个正方形ABCD和OEFG如图10-5所示放置,点O是正方形ABCD对角线的交点.若将正方形OEFG绕点O逆时针旋转120°,两个正方形重叠部分的面积 ( )
A. 不变
B. 先增大再减小
C. 先减小再增大
D. 不断增大
图10-5
A
例14. (教材改编)如图10-6,在半径AC为2,圆心角为90°的扇形内,以BC为直径作半圆,交弦AB于点D,连接CD,则图中阴影部分的面积是
.
图10-6
π-1
8 猜想归纳法
通过题目条件进行推理,寻找规律,从而归纳出正确答案的方法.
例15. (2024·云南)按一定规律排列的代数式:2x,3x2,4x3,5x4,6x5,…,第n个代数式是( )
A. 2xn B. (n-1)xn C. nxn+1 D. (n+1)xn
D
例16. (2024·青海)如图10-7是由火柴棒摆成的图案,按此规律摆放,第⑦个图案中有 根火柴棒.
图10-7
15
选填题常用方法
第十章 选填题突破
选填题常用方法
选择题和填空题都具有构思巧妙、概念性强、知识容量大、覆盖面广且评分标准统一等优点,因而历来是中考数学的重要题型,要想迅速、正确地解题,除了要有准确的计算、严密的推理外,还必须掌握其解题方法与技巧,下面介绍选填的几种常用方法.
1 直接法
直接从题目条件出发,运用相关的性质、定理、法则、公式等,通过准确运算、严密推理和合理验证,最后得出正确的结果,运用此方法解题需要扎实的数学基础.
例1. (2024·南通)如果零上2 ℃记作+2 ℃,那么零下3 ℃记作 ( )
A. -3 ℃ B. 3 ℃ C. -5 ℃ D. 5 ℃
例2. (2024·福建)因式分解:x2+x= .
A
x(x+1)
2 检验法
将选项分别代入题设中或将题设代入选项中检验,然后选择符合题设条件的选项的一种方法.当结论为具体值时可考虑使用检验法,在运用检验法时,若能根据题意确定代入顺序,则更能提高解题速度,反之会造成计算和推理量过大.
D
(答案不唯一)
3 排除筛选法
对于正确答案只有一个的选择题,根据题设条件和有关知识,通过分析、推理、演算等,筛除一些较易判定的、不合题意的结论,缩小选择的范围,再从其余结论中求得正确答案.这种方法适用于定性或不易求解的选择题,它与特殊值法、数形结合法等结合使用是选择题的常规方法.
B
例6. (教材改编)如图10-1,在四边形ABCD中,AB∥CD,对角线AC与BD相交于点O,以下四个结论:
①△AOB∽△COD;
②△AOD∽△ACB;
③S△DOC∶S△AOD=DC∶AB;
④S△AOD=S△BOC.
其中一定正确的有 .
图10-1
①③④
4 特殊值法
根据题设情况,选取满足条件的特殊数值、特殊的点、特殊的图形或特殊的位置状态,代替题设的普遍条件,将一般形式转化为特殊形式进行求解的方法.
例7. (教材改编)已知x+y+z=0,则(x+y)(y+z)(z+x)+xyz的值为 ( )
A. 1 B. 0 C. 3 D. -1
B
例8. (教材改编)如图10-2,矩形ABCD的面积为1,E,F,G,H分别为四条边的中点,I是FE上任一动点,则阴影部分的面积为 .
图10-2
5 整体代入法
把某个式子看作一个整体代入原有的问题中,从而简化问题得到答案的一种方法.在求多项式的值的问题中,若字母的取值不知道或不易求出,即可采用该方法巧妙求出多项式的值.
例9. (2023·常德)若a2+3a-4=0,则2a2+6a-3= ( )
A. 5 B. 1 C. -1 D. 0
例10. (2024·苏州)若a=b+2,则(b-a)2= .
A
4
6 数形结合法
数形结合法是利用函数图象或某些特殊值的几何意义,将代数的问题(如解方程、解不等式、求最值、求取值范围等)与几何图形相结合,数与形相互转化,使问题化繁为简,从而确定正确答案的方法.
图10-3
A
图10-4
B
7 等价转化法
通过观察、分析、类比、联想等,借助某些性质、公式或已知条件,选择恰当的数学方法将某些问题进行转化,由复杂转化为简单,由未知转化为已知,由抽象转化为具体,从而进行计算.
例13. (教材改编)边长相等的两个正方形ABCD和OEFG如图10-5所示放置,点O是正方形ABCD对角线的交点.若将正方形OEFG绕点O逆时针旋转120°,两个正方形重叠部分的面积 ( )
A. 不变
B. 先增大再减小
C. 先减小再增大
D. 不断增大
图10-5
A
例14. (教材改编)如图10-6,在半径AC为2,圆心角为90°的扇形内,以BC为直径作半圆,交弦AB于点D,连接CD,则图中阴影部分的面积是
.
图10-6
π-1
8 猜想归纳法
通过题目条件进行推理,寻找规律,从而归纳出正确答案的方法.
例15. (2024·云南)按一定规律排列的代数式:2x,3x2,4x3,5x4,6x5,…,第n个代数式是( )
A. 2xn B. (n-1)xn C. nxn+1 D. (n+1)xn
D
例16. (2024·青海)如图10-7是由火柴棒摆成的图案,按此规律摆放,第⑦个图案中有 根火柴棒.
图10-7
15
同课章节目录
