中考数学复习知识梳理第一章数与式第1课时实数及其运算课件(共38张PPT)
文档属性
| 名称 | 中考数学复习知识梳理第一章数与式第1课时实数及其运算课件(共38张PPT) |  | |
| 格式 | ppt | ||
| 文件大小 | 3.9MB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 通用版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2025-05-31 09:26:04 | ||
图片预览










文档简介
(共38张PPT)
第一章 数与式
第1课时 实数及其运算
课前循环练
(限时5分钟,3个选择+2个填空,训练中考客观题准确度与速度)
A
A
B
1
5. (广东真题)已知实数a,b在数轴上的对应点的位置如图1-1-1所示,则a+b 0. (填“>” “<”或“=”)
>
课标要求
(1)有理数
①理解负数的意义;理解有理数的意义,能用数轴上的点表示有理数,能比较有理数的大小.
②借助数轴理解相反数和绝对值的意义,掌握求有理数的相反数和绝对值的方法.
③理解乘方的意义.
④掌握有理数的加、减、乘、除、乘方及简单的混合运算(以三步以内为主);理解有理数的运算律,能运用运算律简化运算.
⑤能运用有理数的运算解决简单问题.
(2)实数
①了解无理数和实数,知道实数由有理数和无理数组成,了解实数与数轴上的点一一对应.
②能用数轴上的点表示实数,能比较实数的大小.
③能借助数轴理解相反数和绝对值的意义,会求实数的相反数和绝对值.
④了解平方根、算术平方根、立方根的概念,会用根号表示数的平方根、算术平方根、立方根.
⑤了解乘方与开方互为逆运算,会用平方运算求百以内完全平方数的平方根,会用立方运算求千以内完全立方数(及对应的负整数)的立方根,会用计算器计算平方根和立方根.
⑥能用有理数估计一个无理数的大致范围.
⑦了解近似数,在解决实际问题中,能用计算器进行近似计算,会按问题的要求进行简单的近似计算.
⑧会用科学记数法表示数(包括在计算器上表示).
对接教材 人教:七上第一章 有理数;七下第六章 实数
北师:七上第二章 有理数及其运算;八上第二章 实数
考点梳理
(学生预习完成,教师课堂精准点拨)
考点复习
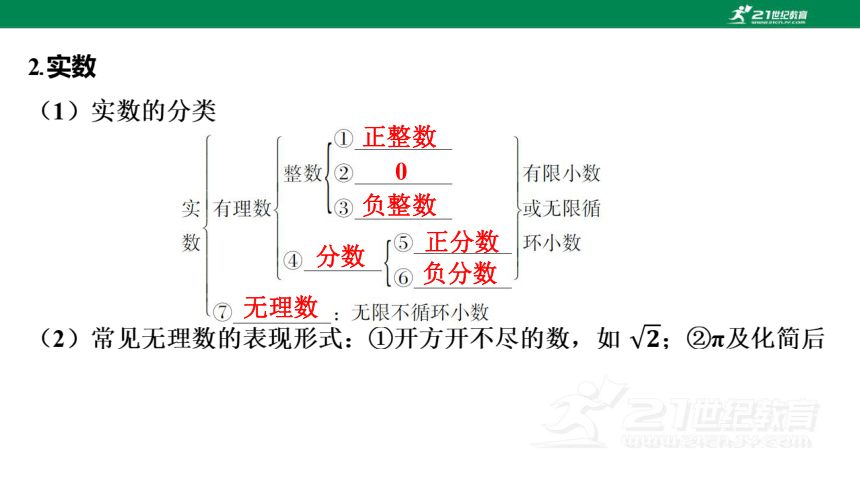
1.正数和负数
(1)大于 的数是正数,小于 的数是负数. 既不是正数,也不是负数.
(2)常用正数和负数表示一组具有 意义的量.如收入(+)与支出(-),零上(+)与零下(-)等
0
0
0
相反
广东省对应考点例题
例1.某仓库记账员为方便记账,将进货10件记作+10件,那么出货5件应记作 件.
-5
正整数
0
负整数
分数
正分数
负分数
无理数
①③④⑤⑥⑧
②⑦⑨
①②④⑤⑧⑨
③⑧
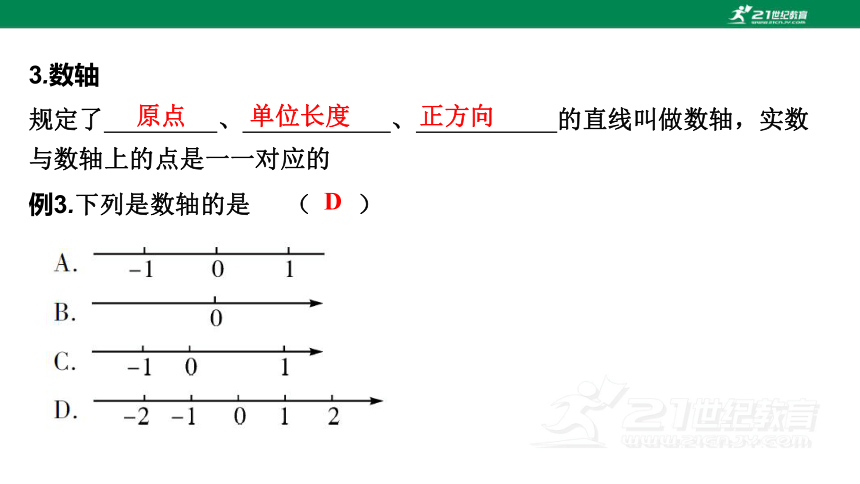
3.数轴
规定了 、 、 的直线叫做数轴,实数与数轴上的点是一一对应的
例3.下列是数轴的是 ( )
原点
单位长度
正方向
D
4.相反数
如果两个数只有 不同,那么称其中一个数为另一个数的相反数,也称这两个数互为相反数.特别地,0的相反数还是0;a+b=0 a,b互为相反数;在数轴上,表示互为相反数的两个点位于原点两侧,且到原点的距离
例4.(1)8的相反数是 ;
(2)0的相反数是 ;
(3)-3的相反数是 .
符号
相等
-8
0
3
距离
相等
例5.(1)4的绝对值是 ;
(2)0的绝对值是 ;
(3)-0.5的绝对值是 .
4
0
0.5
1
0
-5
7.实数的大小比较
(1)数轴上两个点表示的数,右边的总比左边的 .
(2)正数 0,负数 0,正数 负数;两个负数比较大小,绝对值大的反而小.
(3)用求差法比较大小:
①若a-b>0,则a b;②若a-b=0,则a b;
③若a-b<0,则a b
大
大于
小于
大于
>
=
<
>
>
<
<
8.实数的运算
(1)实数运算法则:先算乘方、开方,再算乘除,最后算加减;有括号的要先算括号内的;若没有括号,在同级运算中,要从左到右依次进行.
(2)常见的运算:
①零指数幂:a0= (a≠0);
②负整数指数幂:a-p= (a≠0,p为正整数);
③乘方:an=a·a·…·a(n个a相乘),其中a是底数,n是指数;
④-1的奇偶次幂:-1的奇数次幂为 ,-1的偶数次幂为
1
-1
1
6
10.平方根、算术平方根及立方根
名称 定义 表示方法 性质
平方根 如果一个数的平方等于a,那么这个数叫做a的平方根 正数的平方根有两个,它们互为相反数;0的平方根是0;负数没有平方根
算术
平方根 如果一个正数的平方等于a,那么这个正数叫做a的算术平方根 正数的算术平方根是正数;0的算术平方根是0;负数没有算术平方根
立方根 如果一个数的立方等于a,那么这个数叫做a的立方根 正数的立方根是正数;0的立方根是0;负数的立方根是负数
C
A
B
a×10n
正整数
负整数
四舍五入
D
3×10-7
8.0
3.142
广东中考
B
D
4. (2023·广东题1,3分,正数和负数)负数的概念最早出现在我国古代著名的数学专著《九章算术》中. 如果把收入5元记作+5元,那么支出5元记作 ( )
A. -5元 B. 0元 C. +5元 D. +10元
5. (2024·广东题3,3分,科学记数法—表示较大的数)2024年6月6日,嫦娥六号在距离地球约384 000 km外上演“太空牵手”,完成月球轨道的交会对接. 数据384 000用科学记数法表示为 ( )
A. 3.84×104 B. 3.84×105 C. 3.84×106 D. 38.4×105
A
B
6. (2024·广东题7,3分,算术平方根)完全相同的4个正方形面积之和是100,则正方形的边长是 ( )
A. 2 B. 5 C. 10 D. 20
B
高分击破
(中考核心例题)
·················4分(零指数幂、绝对值、算术平方根、负指数幂的化简各得1分)
·······························································5分(计算乘法得1分)
··········································································7分(计算结果得2分)
温馨提示:此类考题常见于广东省中考数学试卷的第16题,分值一般为7分,答题时要注意书写格式,分步书写,慢做会求全对,评卷老师是分步给的哦!
错解分析
错解:原式=(-2)÷2 025-2 025
=(-2)÷0
=0.
剖析:该解答过程没有理解一个数的-1次幂就是该数的倒数,任何非零数的0次幂都等于1,没掌握-1的奇数幂是-1,-1的偶数幂是1,而且没有根据运算法则,先算乘方,再算乘除,最后算加减,所以导致解题错误.
【生长式训练】知识生长→变式创新
3. (中考创新,原创题)已知a,b互为相反数,c,d互为倒数,m是绝对值最小的数,n是最小的正整数.
知识种子:基本概念
(1)填空:a+b= ,cd= ,m= ,n= ;
0
1
0
1
中考演练
(中考核心素养训练,限时15分钟)
一、选择题
1. (2024·天津)计算3-(-3)的结果等于 ( )
A. -6 B. 0 C. 3 D. 6
2. (2024·广州)四个数-10,-1,0,10中,最小的数是 ( )
A. -10 B. -1 C. 0 D. 10
D
A
3. (2024·赤峰)央视新闻2024年5月31日报道,世界最大清洁能源走廊今年一季度累计发电超52 000 000 000度,为我国经济社会绿色发展提供了强劲动能. 将数据52 000 000 000用科学记数法表示为 ( )
A. 5.2×109 B. 0.52×1011 C. 52×10-9 D. 5.2×1010
D
4. (2024·深圳)如图1-1-3,实数a,b,c,d在数轴上表示如下,则最小的实数为 ( )
A. a B. b
C. c D. d
A
B
二、填空题
6. (2024·湖南)计算:-(-2 024)= .
7. (2024·巴中)27的立方根是 .
8. (2024·连云港)如果公元前121年记作-121年,那么公元2024年应记作
年.
2 024
3
+2 024
命题趋势
(对 2025 年中考进行预测,创新题型,限时 5 分钟)
命题解读:根据最新课程标准和近三年中考命题动向,预测2025年中考命题方向可能注重对实数基本概念的考查,如相反数、绝对值、平方根、算术平方根、立方根、科学记数法等;强调实数的运算,核心是考查实数的混合运算,常与绝对值、二次根式、幂的运算、特殊锐角三角函数等结合在一起考查.
第一章 数与式
第1课时 实数及其运算
课前循环练
(限时5分钟,3个选择+2个填空,训练中考客观题准确度与速度)
A
A
B
1
5. (广东真题)已知实数a,b在数轴上的对应点的位置如图1-1-1所示,则a+b 0. (填“>” “<”或“=”)
>
课标要求
(1)有理数
①理解负数的意义;理解有理数的意义,能用数轴上的点表示有理数,能比较有理数的大小.
②借助数轴理解相反数和绝对值的意义,掌握求有理数的相反数和绝对值的方法.
③理解乘方的意义.
④掌握有理数的加、减、乘、除、乘方及简单的混合运算(以三步以内为主);理解有理数的运算律,能运用运算律简化运算.
⑤能运用有理数的运算解决简单问题.
(2)实数
①了解无理数和实数,知道实数由有理数和无理数组成,了解实数与数轴上的点一一对应.
②能用数轴上的点表示实数,能比较实数的大小.
③能借助数轴理解相反数和绝对值的意义,会求实数的相反数和绝对值.
④了解平方根、算术平方根、立方根的概念,会用根号表示数的平方根、算术平方根、立方根.
⑤了解乘方与开方互为逆运算,会用平方运算求百以内完全平方数的平方根,会用立方运算求千以内完全立方数(及对应的负整数)的立方根,会用计算器计算平方根和立方根.
⑥能用有理数估计一个无理数的大致范围.
⑦了解近似数,在解决实际问题中,能用计算器进行近似计算,会按问题的要求进行简单的近似计算.
⑧会用科学记数法表示数(包括在计算器上表示).
对接教材 人教:七上第一章 有理数;七下第六章 实数
北师:七上第二章 有理数及其运算;八上第二章 实数
考点梳理
(学生预习完成,教师课堂精准点拨)
考点复习
1.正数和负数
(1)大于 的数是正数,小于 的数是负数. 既不是正数,也不是负数.
(2)常用正数和负数表示一组具有 意义的量.如收入(+)与支出(-),零上(+)与零下(-)等
0
0
0
相反
广东省对应考点例题
例1.某仓库记账员为方便记账,将进货10件记作+10件,那么出货5件应记作 件.
-5
正整数
0
负整数
分数
正分数
负分数
无理数
①③④⑤⑥⑧
②⑦⑨
①②④⑤⑧⑨
③⑧
3.数轴
规定了 、 、 的直线叫做数轴,实数与数轴上的点是一一对应的
例3.下列是数轴的是 ( )
原点
单位长度
正方向
D
4.相反数
如果两个数只有 不同,那么称其中一个数为另一个数的相反数,也称这两个数互为相反数.特别地,0的相反数还是0;a+b=0 a,b互为相反数;在数轴上,表示互为相反数的两个点位于原点两侧,且到原点的距离
例4.(1)8的相反数是 ;
(2)0的相反数是 ;
(3)-3的相反数是 .
符号
相等
-8
0
3
距离
相等
例5.(1)4的绝对值是 ;
(2)0的绝对值是 ;
(3)-0.5的绝对值是 .
4
0
0.5
1
0
-5
7.实数的大小比较
(1)数轴上两个点表示的数,右边的总比左边的 .
(2)正数 0,负数 0,正数 负数;两个负数比较大小,绝对值大的反而小.
(3)用求差法比较大小:
①若a-b>0,则a b;②若a-b=0,则a b;
③若a-b<0,则a b
大
大于
小于
大于
>
=
<
>
>
<
<
8.实数的运算
(1)实数运算法则:先算乘方、开方,再算乘除,最后算加减;有括号的要先算括号内的;若没有括号,在同级运算中,要从左到右依次进行.
(2)常见的运算:
①零指数幂:a0= (a≠0);
②负整数指数幂:a-p= (a≠0,p为正整数);
③乘方:an=a·a·…·a(n个a相乘),其中a是底数,n是指数;
④-1的奇偶次幂:-1的奇数次幂为 ,-1的偶数次幂为
1
-1
1
6
10.平方根、算术平方根及立方根
名称 定义 表示方法 性质
平方根 如果一个数的平方等于a,那么这个数叫做a的平方根 正数的平方根有两个,它们互为相反数;0的平方根是0;负数没有平方根
算术
平方根 如果一个正数的平方等于a,那么这个正数叫做a的算术平方根 正数的算术平方根是正数;0的算术平方根是0;负数没有算术平方根
立方根 如果一个数的立方等于a,那么这个数叫做a的立方根 正数的立方根是正数;0的立方根是0;负数的立方根是负数
C
A
B
a×10n
正整数
负整数
四舍五入
D
3×10-7
8.0
3.142
广东中考
B
D
4. (2023·广东题1,3分,正数和负数)负数的概念最早出现在我国古代著名的数学专著《九章算术》中. 如果把收入5元记作+5元,那么支出5元记作 ( )
A. -5元 B. 0元 C. +5元 D. +10元
5. (2024·广东题3,3分,科学记数法—表示较大的数)2024年6月6日,嫦娥六号在距离地球约384 000 km外上演“太空牵手”,完成月球轨道的交会对接. 数据384 000用科学记数法表示为 ( )
A. 3.84×104 B. 3.84×105 C. 3.84×106 D. 38.4×105
A
B
6. (2024·广东题7,3分,算术平方根)完全相同的4个正方形面积之和是100,则正方形的边长是 ( )
A. 2 B. 5 C. 10 D. 20
B
高分击破
(中考核心例题)
·················4分(零指数幂、绝对值、算术平方根、负指数幂的化简各得1分)
·······························································5分(计算乘法得1分)
··········································································7分(计算结果得2分)
温馨提示:此类考题常见于广东省中考数学试卷的第16题,分值一般为7分,答题时要注意书写格式,分步书写,慢做会求全对,评卷老师是分步给的哦!
错解分析
错解:原式=(-2)÷2 025-2 025
=(-2)÷0
=0.
剖析:该解答过程没有理解一个数的-1次幂就是该数的倒数,任何非零数的0次幂都等于1,没掌握-1的奇数幂是-1,-1的偶数幂是1,而且没有根据运算法则,先算乘方,再算乘除,最后算加减,所以导致解题错误.
【生长式训练】知识生长→变式创新
3. (中考创新,原创题)已知a,b互为相反数,c,d互为倒数,m是绝对值最小的数,n是最小的正整数.
知识种子:基本概念
(1)填空:a+b= ,cd= ,m= ,n= ;
0
1
0
1
中考演练
(中考核心素养训练,限时15分钟)
一、选择题
1. (2024·天津)计算3-(-3)的结果等于 ( )
A. -6 B. 0 C. 3 D. 6
2. (2024·广州)四个数-10,-1,0,10中,最小的数是 ( )
A. -10 B. -1 C. 0 D. 10
D
A
3. (2024·赤峰)央视新闻2024年5月31日报道,世界最大清洁能源走廊今年一季度累计发电超52 000 000 000度,为我国经济社会绿色发展提供了强劲动能. 将数据52 000 000 000用科学记数法表示为 ( )
A. 5.2×109 B. 0.52×1011 C. 52×10-9 D. 5.2×1010
D
4. (2024·深圳)如图1-1-3,实数a,b,c,d在数轴上表示如下,则最小的实数为 ( )
A. a B. b
C. c D. d
A
B
二、填空题
6. (2024·湖南)计算:-(-2 024)= .
7. (2024·巴中)27的立方根是 .
8. (2024·连云港)如果公元前121年记作-121年,那么公元2024年应记作
年.
2 024
3
+2 024
命题趋势
(对 2025 年中考进行预测,创新题型,限时 5 分钟)
命题解读:根据最新课程标准和近三年中考命题动向,预测2025年中考命题方向可能注重对实数基本概念的考查,如相反数、绝对值、平方根、算术平方根、立方根、科学记数法等;强调实数的运算,核心是考查实数的混合运算,常与绝对值、二次根式、幂的运算、特殊锐角三角函数等结合在一起考查.
同课章节目录
