中考数学复习知识梳理第四章三角形第15课时等腰三角形、等边三角形、直角三角形课件(共52张PPT)
文档属性
| 名称 | 中考数学复习知识梳理第四章三角形第15课时等腰三角形、等边三角形、直角三角形课件(共52张PPT) |  | |
| 格式 | ppt | ||
| 文件大小 | 4.6MB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 通用版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2025-05-31 09:28:31 | ||
图片预览








文档简介
(共52张PPT)
第四章 三 角 形
第15课时 等腰三角形、等边三角形、直角三角形
课前循环练
(限时5分钟)
1. (广东真题)关于x的方程2(x-1)-a=0的根是3,则a的值为( )
A. 4 B. -4 C. 5 D. -5
A
图4-15-1
D
3. (广东真题)下列说法正确的是 ( )
A. 有两边和其中一边的对角对应相等的两个三角形全等
B. 等腰三角形是轴对称图形,也是中心对称图形
C. 对角线互相平分的四边形是平行四边形
D. 有两边平行的四边形是梯形
C
图4-15-2
30°
10
①理解等腰三角形的概念,探索并证明等腰三角形的性质定理:等腰三角形的两个底角相等;底边上的高线、中线及顶角平分线重合. 探索并掌握等腰三角形的判定定理:有两个角相等的三角形是等腰三角形. 探索等边三角形的性质定理:等边三角形的各角都等于60°. 探索等边三角形的判定定理:三个角都相等的三角形(或有一个角是60°的等腰三角形)是等边三角形.
②理解直角三角形的概念,探索并掌握直角三角形的性质定理:直角三角形的两个锐角互余,直角三角形斜边上的中线等于斜边的一半.掌握有两个角互余的三角形是直角三角形.
课标要求
③探索勾股定理及其逆定理,并能运用它们解决一些简单的实际问题.
④探索并证明角平分线的性质定理:角平分线上的点到角两边的距离相等;反之,角的内部到角两边距离相等的点在角的平分线上.
⑤理解线段垂直平分线的概念,探索并证明线段垂直平分线的性质定理:线段垂直平分线上的点到线段两端的距离相等;反之,到线段两端距离相等的点在线段的垂直平分线上.
对接教材 人教:八上第十三章 轴对称(13.3等腰三角形);八下第十七章 勾股定理
北师:八上第一章 勾股定理;八下第一章 三角形的证明
考点梳理
广东省对应考点例题
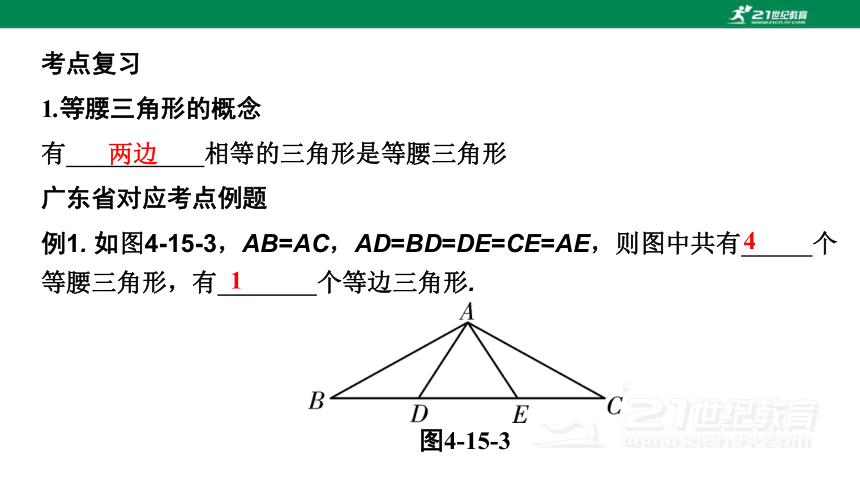
例1. 如图4-15-3,AB=AC,AD=BD=DE=CE=AE,则图中共有 个等腰三角形,有 个等边三角形.
图4-15-3
4
1
考点复习
1.等腰三角形的概念
有 相等的三角形是等腰三角形
两边
2.等腰三角形的性质
(1)等腰三角形的两条腰 ,两个底角 ,简称等边对等角.
(2)等腰三角形顶角的 、底边上的 及底边上的高线互相重合,简称“三线合一”.
(3)等腰三角形是轴对称图形,有 条对称轴
相等
相等
平分线
中线
1
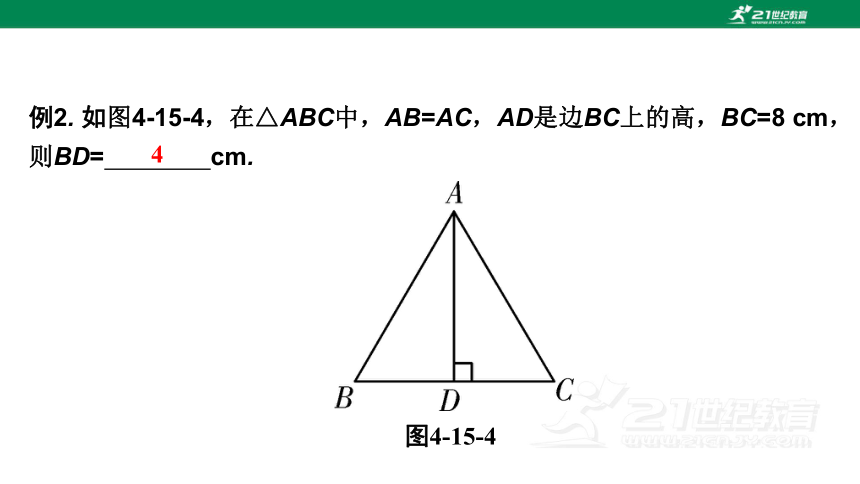
例2. 如图4-15-4,在△ABC中,AB=AC,AD是边BC上的高,BC=8 cm,则BD= cm.
图4-15-4
4
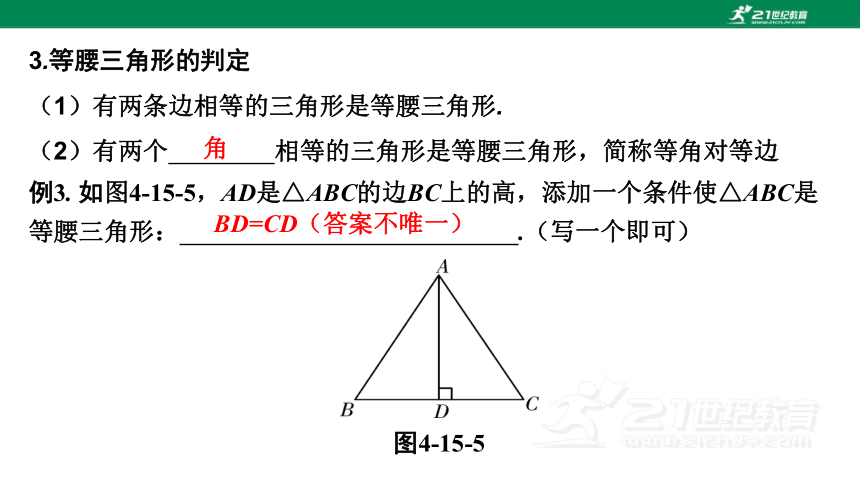
3.等腰三角形的判定
(1)有两条边相等的三角形是等腰三角形.
(2)有两个 相等的三角形是等腰三角形,简称等角对等边
角
例3. 如图4-15-5,AD是△ABC的边BC上的高,添加一个条件使△ABC是等腰三角形: .(写一个即可)
图4-15-5
BD=CD(答案不唯一)
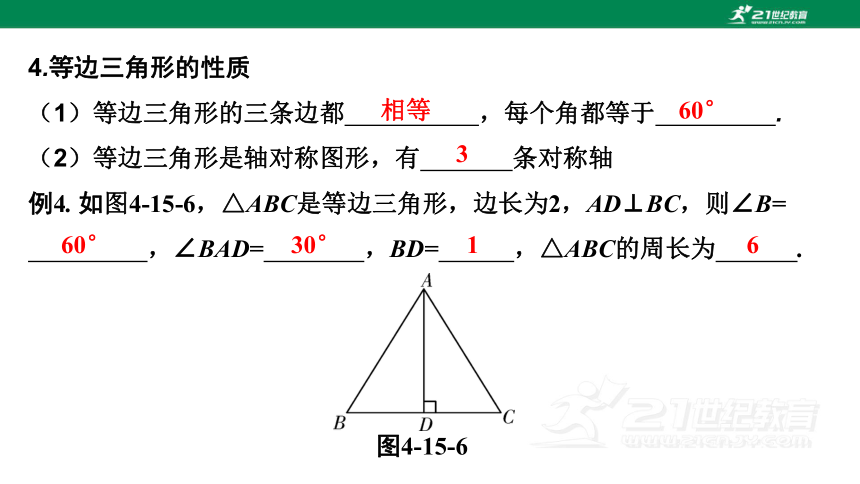
4.等边三角形的性质
(1)等边三角形的三条边都 ,每个角都等于 .
(2)等边三角形是轴对称图形,有 条对称轴
相等
60°
3
例4. 如图4-15-6,△ABC是等边三角形,边长为2,AD⊥BC,则∠B=
,∠BAD= ,BD= ,△ABC的周长为 .
图4-15-6
60°
30°
1
6
5.等边三角形的判定
(1)三条边都相等的三角形是等边三角形.
(2)三个角都相等的三角形是等边三角形.
(3)有一个角等于60°的 是等边三角形.
(4)有两个角等于 的三角形是等边三角形
等腰三角形
60°
例5. 在△ABC中,如果AB=AC, (只添加一个条件),则△ABC为等边三角形.
BC=AB(答案不唯一)
6.直角三角形的性质
(1)直角三角形的两个锐角 .
(2)直角三角形斜边上的中线等于斜边的 .
(3)在直角三角形中,如果一个锐角等于30°,那么它所对的直角边等于 .
(4)在直角三角形中,如果一条直角边等于斜边的一半,那么这条直角边所对的角等于 .(解答题需证明使用)
(5)勾股定理:直角三角形的两条直角边的平方和等于斜边的
互余
一半
斜边的一半
30°
平方
例6. (1)如图4-15-7,在Rt△ABC中,∠ABC=90°.若AC=2BC,则
∠A= ;若D为斜边AC的中点,且AC=5,则BD= ;
30°
图4-15-7
(2)如图4-15-8,在△ABC中,∠C=90°,∠B=15°,DE垂直平分AB,交BC于点E,BE=4,则∠EAC= ,AC= ;
(3)在Rt△ABC中,∠C=90°,BC=1,AC=2,则AB的长是 .
图4-15-8
60°
2
7.直角三角形的判定
(1)有一个角是 的三角形是直角三角形.
(2)有两个角 的三角形是直角三角形.
(3)勾股定理的逆定理:如果三角形两边的平方和等于第三边的平方,那么这个三角形是直角三角形.
(4)如果三角形一边上的 等于这边的一半,那么这个三角形是直角三角形(解答题需证明使用)
90°
互余
中线
例7. (1)如图4-15-9,已知P是射线ON上一动点(即点P可在射线ON上运动),若∠AON=30°,则当∠A= 时,△AOP是直角三角形;
图4-15-9
60°或90°
(2)如图4-15-10,在△ABC中,AD=DC=BD,则∠ABC= .
图4-15-10
90°
8.角平分线的性质与判定
(1)性质定理:角平分线上的点到这个角的两边的距离 .
(2)判定定理:在一个角的内部,到角的两边距离 的点在这个角的平分线上
相等
相等
例8. 如图4-15-11,在Rt△ABC中,∠C=90°,AD是∠BAC的平分线,DC=2,AB=6,则△ABD的面积为 .
图4-15-11
6
9.线段的垂直平分线
(1)线段的垂直平分线:垂直于一条线段,并且平分这条线段的直线叫做这条线段的垂直平分线.
(2)性质定理:线段垂直平分线上的点到这条线段两个端点的距离____
.
(3)判定定理:到一条线段两个端点距离相等的点,在这条线段的____
上
相等
垂直平分线
例9. 如图4-15-12,在△ABC中,边AB的中垂线分别交BC,AB于点D,E,AE=3 cm,△ADC的周长为9 cm,则△ABC的周长是 cm.
图4-15-12
15
广东中考
1. (2020·广东题17,4分,直角三角形斜边上的中线;点与圆的位置关系)有一架竖直靠在直角墙面的梯子正在下滑,一只猫紧紧盯住位于梯子正中间的老鼠,等待与老鼠距离最小时扑捉. 把墙面、梯子、猫和老鼠都理想化为同一平面内的线或点,模型如图4-15-13.∠ABC=90°,点M,N分别在射线BA,BC上,MN长度始终保持不变,MN=4,E
为MN的中点,点D到BA,BC的距离分别为4和2. 在此滑
动过程中,猫与老鼠的距离DE的最小值为 .
图4-15-13
2. (2021·广东题20,6分, 解直角三角形;线段垂直平分线的性质)如图4-15-14,在Rt△ABC中,∠A=90°,作BC的垂直平分线交AC于点D,延长AC至点E,使CE=AB.
(1)若AE=1,求△ABD的周长;
图4-15-14
解:(1)作图如答图4-15-1,连接BD.
∴BD=CD.
∵AB=CE,
∴△ABD的周长为AB+AD+BD=CE+AD+CD=AE=1.
答图4-15-1
答图4-15-1
高分击破
【典型考点】等腰三角形的判定 得分点分析
1. (2020·广东)如图4-15-15,在△ABC中,点D,E分别是边AB,AC上的点,BD=CE,∠ABE=∠ACD,BE与CD相交于点F.求证:△ABC是等腰三角形.
图4-15-15
温馨提示:此类考题常见于广东省中考数学试卷的第18题,分值一般为7分,答题时要注意书写格式,分步书写,慢做会求全对,评卷老师是分步给分的哦!
【典型错例】等腰三角形性质的综合运用漏解
2. 等腰三角形一腰上的高与另一腰的夹角为50°,求该等腰三角形顶角的度数.
解:①如答图4-15-2,当等腰三角形ABC为锐角三角形时,
∵∠ABD=50°,BD⊥AC,
∴∠A=90°-∠ABD=40°.
∴此时三角形的顶角为40°;
答图4-15-2
②如答图4-15-3,当等腰三角形ABC为钝角三角形时,
∵BD⊥AC,∴∠BDA=90°.
∵∠ABD=50°,∴∠BAC=∠ABD+∠BDA=140°.
∴此时三角形的顶角为140°.
综上所述,该等腰三角形顶角的度数为40°或140°.
答图4-15-3
错解分析
错解:如图4-15-16,在等腰三角形ABC中,AB=AC,BD为AC边上的高.
由题意知∠ABD=50°,
∴∠A=90°-∠ABD=40°. ∴该等腰三角形顶角的度数为40°.
剖析:该解答过程的错误在于直接默认等腰三角形是锐角三角形,忽视了还有钝角三角形的情况.本题要进行分类讨论,分等腰三角形的顶角是锐角和等腰三角形的顶角是钝角两种情况,再分别解答.
图4-15-16
【生长式训练】知识生长→变式创新
3. (中考创新,原创题)如图4-15-17,△ACB和△DCE均是顶角为40°的等腰三角形,AB,DE分别是底边,连接AD,BE,点A,D,E在同一直线上.
知识种子:基本概念
(1)填空:∠BAC= ,∠ADC= ;
图4-15-17
70°
110°
种子生长:等腰三角形的性质
(2)求证:AD=BE;
图4-15-17
生长变式:图形变式
(3)如图4-15-18,若△ACB和△DCE均是等边三角形,连接AD,BE,点A,D,E在同一直线上.
①求∠AEB的度数;
图4-15-18
①∵∠CDE=60°,点A,D,E在同一直线上,
∴∠ADC=180°-∠CDE=120°.
∴∠BEC=∠ADC =120°.
∵∠CED=60°,
∴∠AEB=∠BEC-∠CED=120°-60°=60°.
图4-15-18
②AE=BE+CE.
理由:∵AE=AD+DE,AD=BE,DE=CE,
∴AE=BE+CE.
图4-15-18
②求线段AE,BE,CE之间的数量关系,并说明理由;
种子成树:综合创新
(4)如图4-15-19,若△ACB和△DCE均为等腰直角三角形,∠ACB=∠DCE=90°,连接AD,BE,点A,D,E在同一直线上,CM为△DCE的边DE上的高.
图4-15-19
图4-15-19
①求∠AEB的度数;
②AE= BE+2CM.
理由:∵CM为△DCE的边DE上的高,∴CM⊥DE.
又∵CD=CE,∴DM=EM.
∵∠DCE=90°,∴DE=2CM.
∵AE=AD+DE,AD=BE,DE=2CM,∴AE=BE+2CM.
图4-15-19
中考演练
(限时15分钟)
一、选择题
1. (2024·青海)如图4-15-20,OC平分∠AOB,点P在OC上,PD⊥OB,PD=2,则点P到OA的距离是 ( )
A. 4 B. 3
C. 2 D. 1
图4-15-20
C
2. (2024·兰州)如图4-15-21,在△ABC中,AB=AC,∠BAC=130°,DA⊥AC,则∠ADB= ( )
A. 100° B. 115°
C. 130° D. 145°
B
图4-15-21
图4-15-22
A
4. (2024·凉山州)如图4-15-23,在Rt△ABC中,∠ACB=90°,DE垂直平分AB交BC于点D.若△ACD的周长为50 cm,则AC+BC= ( )
A. 25 cm B. 45 cm
C. 50 cm D. 55 cm
图4-15-23
C
图4-15-24
C
二、填空题
6. (2023·丽水)如图4-15-25,在△ABC中,AC的垂直平分线交BC于点D,交AC于点E,∠B=∠ADB. 若AB=4,则DC的长是 .
图4-15-25
4
7. (2024·重庆)如图4-15-26,在△ABC中,AB=AC,∠A=36°,BD平分∠ABC交AC于点D. 若BC=2,则AD的长度为 .
图4-15-26
2
8. (2023·随州)如图4-15-27,在Rt△ABC中,∠C=90°,AC=8,BC=6,D为AC上一点,若BD是∠ABC的平分线,则AD= .
图4-15-27
5
三、解答题
9. (2024·宜宾)如图4-15-28,D,E分别是等边三角形ABC边BC,AC上的点,且BD=CE,BE与AD交于点F. 求证:AD=BE.
图4-15-28
10. (2022·温州)如图4-15-29,BD是△ABC的角平分线,DE∥BC,交AB于点E.
(1)求证:∠EBD=∠EDB;
(1)证明:∵BD是△ABC的角平分线,∴∠CBD=∠EBD.
∵DE∥BC,∴∠CBD=∠EDB. ∴∠EBD=∠EDB.
图4-15-29
(2)当AB=AC时,请判断CD与ED的大小关系,并说明理由.
(2)解:CD=ED.
理由:∵AB=AC,∴∠ABC=∠C.
∵DE∥BC,∴∠ADE=∠C,∠AED=∠ABC. ∴∠ADE=∠AED.
∴AD=AE. ∴AC-AD=AB-AE,即CD=BE.
由(1)知∠EBD=∠EDB,∴BE=ED. ∴CD=ED.
图4-15-29
命题趋势
( 限时 5 分钟)
(教材改编)如图4-15-30,在△ABC中,DE是边BC的垂直平分线,分别交边AC,BC于点D,E,BF⊥AC,且F是线段AD的中点,延长BF与BC的垂直平分线交于点G,连接CG.
(1)若D是AC的中点,求证:AC=2AB;
证明:(1)如答图4-15-4,连接BD.
∵DE是边BC的垂直平分线,∴DB=DC.
∵BF⊥AC,F是AD的中点,∴AB=DB.
∴AB=DC.
又∵D是AC的中点,∴AC=2DC=2AB.
图4-15-30
答图4-15-4
(2)若∠ACB=30°,求证:△BGC为等边三角形.
(2)∵DE是边BC的垂直平分线,
∴BG=CG.
∴△BGC为等腰三角形.
∵BF⊥AC,∴∠BFC=90°.
∵∠ACB=30°,
∴∠GBC=90°-∠ACB=60°.
∴△BGC为等边三角形.
图4-15-30
命题解读:根据最新课程标准和近三年中考命题动向,预测2025年中考命题方向可能注重考查等腰三角形、等边三角形、直角三角形的基本概念、性质和判定方法;注重考查角平分线、垂直平分线的性质,可能会结合尺规作图一起考查;强调与其他知识点的综合考查,如与三角形的全等、相似、三角函数、圆等结合;还可能会结合实际生活情境进行考查.
第四章 三 角 形
第15课时 等腰三角形、等边三角形、直角三角形
课前循环练
(限时5分钟)
1. (广东真题)关于x的方程2(x-1)-a=0的根是3,则a的值为( )
A. 4 B. -4 C. 5 D. -5
A
图4-15-1
D
3. (广东真题)下列说法正确的是 ( )
A. 有两边和其中一边的对角对应相等的两个三角形全等
B. 等腰三角形是轴对称图形,也是中心对称图形
C. 对角线互相平分的四边形是平行四边形
D. 有两边平行的四边形是梯形
C
图4-15-2
30°
10
①理解等腰三角形的概念,探索并证明等腰三角形的性质定理:等腰三角形的两个底角相等;底边上的高线、中线及顶角平分线重合. 探索并掌握等腰三角形的判定定理:有两个角相等的三角形是等腰三角形. 探索等边三角形的性质定理:等边三角形的各角都等于60°. 探索等边三角形的判定定理:三个角都相等的三角形(或有一个角是60°的等腰三角形)是等边三角形.
②理解直角三角形的概念,探索并掌握直角三角形的性质定理:直角三角形的两个锐角互余,直角三角形斜边上的中线等于斜边的一半.掌握有两个角互余的三角形是直角三角形.
课标要求
③探索勾股定理及其逆定理,并能运用它们解决一些简单的实际问题.
④探索并证明角平分线的性质定理:角平分线上的点到角两边的距离相等;反之,角的内部到角两边距离相等的点在角的平分线上.
⑤理解线段垂直平分线的概念,探索并证明线段垂直平分线的性质定理:线段垂直平分线上的点到线段两端的距离相等;反之,到线段两端距离相等的点在线段的垂直平分线上.
对接教材 人教:八上第十三章 轴对称(13.3等腰三角形);八下第十七章 勾股定理
北师:八上第一章 勾股定理;八下第一章 三角形的证明
考点梳理
广东省对应考点例题
例1. 如图4-15-3,AB=AC,AD=BD=DE=CE=AE,则图中共有 个等腰三角形,有 个等边三角形.
图4-15-3
4
1
考点复习
1.等腰三角形的概念
有 相等的三角形是等腰三角形
两边
2.等腰三角形的性质
(1)等腰三角形的两条腰 ,两个底角 ,简称等边对等角.
(2)等腰三角形顶角的 、底边上的 及底边上的高线互相重合,简称“三线合一”.
(3)等腰三角形是轴对称图形,有 条对称轴
相等
相等
平分线
中线
1
例2. 如图4-15-4,在△ABC中,AB=AC,AD是边BC上的高,BC=8 cm,则BD= cm.
图4-15-4
4
3.等腰三角形的判定
(1)有两条边相等的三角形是等腰三角形.
(2)有两个 相等的三角形是等腰三角形,简称等角对等边
角
例3. 如图4-15-5,AD是△ABC的边BC上的高,添加一个条件使△ABC是等腰三角形: .(写一个即可)
图4-15-5
BD=CD(答案不唯一)
4.等边三角形的性质
(1)等边三角形的三条边都 ,每个角都等于 .
(2)等边三角形是轴对称图形,有 条对称轴
相等
60°
3
例4. 如图4-15-6,△ABC是等边三角形,边长为2,AD⊥BC,则∠B=
,∠BAD= ,BD= ,△ABC的周长为 .
图4-15-6
60°
30°
1
6
5.等边三角形的判定
(1)三条边都相等的三角形是等边三角形.
(2)三个角都相等的三角形是等边三角形.
(3)有一个角等于60°的 是等边三角形.
(4)有两个角等于 的三角形是等边三角形
等腰三角形
60°
例5. 在△ABC中,如果AB=AC, (只添加一个条件),则△ABC为等边三角形.
BC=AB(答案不唯一)
6.直角三角形的性质
(1)直角三角形的两个锐角 .
(2)直角三角形斜边上的中线等于斜边的 .
(3)在直角三角形中,如果一个锐角等于30°,那么它所对的直角边等于 .
(4)在直角三角形中,如果一条直角边等于斜边的一半,那么这条直角边所对的角等于 .(解答题需证明使用)
(5)勾股定理:直角三角形的两条直角边的平方和等于斜边的
互余
一半
斜边的一半
30°
平方
例6. (1)如图4-15-7,在Rt△ABC中,∠ABC=90°.若AC=2BC,则
∠A= ;若D为斜边AC的中点,且AC=5,则BD= ;
30°
图4-15-7
(2)如图4-15-8,在△ABC中,∠C=90°,∠B=15°,DE垂直平分AB,交BC于点E,BE=4,则∠EAC= ,AC= ;
(3)在Rt△ABC中,∠C=90°,BC=1,AC=2,则AB的长是 .
图4-15-8
60°
2
7.直角三角形的判定
(1)有一个角是 的三角形是直角三角形.
(2)有两个角 的三角形是直角三角形.
(3)勾股定理的逆定理:如果三角形两边的平方和等于第三边的平方,那么这个三角形是直角三角形.
(4)如果三角形一边上的 等于这边的一半,那么这个三角形是直角三角形(解答题需证明使用)
90°
互余
中线
例7. (1)如图4-15-9,已知P是射线ON上一动点(即点P可在射线ON上运动),若∠AON=30°,则当∠A= 时,△AOP是直角三角形;
图4-15-9
60°或90°
(2)如图4-15-10,在△ABC中,AD=DC=BD,则∠ABC= .
图4-15-10
90°
8.角平分线的性质与判定
(1)性质定理:角平分线上的点到这个角的两边的距离 .
(2)判定定理:在一个角的内部,到角的两边距离 的点在这个角的平分线上
相等
相等
例8. 如图4-15-11,在Rt△ABC中,∠C=90°,AD是∠BAC的平分线,DC=2,AB=6,则△ABD的面积为 .
图4-15-11
6
9.线段的垂直平分线
(1)线段的垂直平分线:垂直于一条线段,并且平分这条线段的直线叫做这条线段的垂直平分线.
(2)性质定理:线段垂直平分线上的点到这条线段两个端点的距离____
.
(3)判定定理:到一条线段两个端点距离相等的点,在这条线段的____
上
相等
垂直平分线
例9. 如图4-15-12,在△ABC中,边AB的中垂线分别交BC,AB于点D,E,AE=3 cm,△ADC的周长为9 cm,则△ABC的周长是 cm.
图4-15-12
15
广东中考
1. (2020·广东题17,4分,直角三角形斜边上的中线;点与圆的位置关系)有一架竖直靠在直角墙面的梯子正在下滑,一只猫紧紧盯住位于梯子正中间的老鼠,等待与老鼠距离最小时扑捉. 把墙面、梯子、猫和老鼠都理想化为同一平面内的线或点,模型如图4-15-13.∠ABC=90°,点M,N分别在射线BA,BC上,MN长度始终保持不变,MN=4,E
为MN的中点,点D到BA,BC的距离分别为4和2. 在此滑
动过程中,猫与老鼠的距离DE的最小值为 .
图4-15-13
2. (2021·广东题20,6分, 解直角三角形;线段垂直平分线的性质)如图4-15-14,在Rt△ABC中,∠A=90°,作BC的垂直平分线交AC于点D,延长AC至点E,使CE=AB.
(1)若AE=1,求△ABD的周长;
图4-15-14
解:(1)作图如答图4-15-1,连接BD.
∴BD=CD.
∵AB=CE,
∴△ABD的周长为AB+AD+BD=CE+AD+CD=AE=1.
答图4-15-1
答图4-15-1
高分击破
【典型考点】等腰三角形的判定 得分点分析
1. (2020·广东)如图4-15-15,在△ABC中,点D,E分别是边AB,AC上的点,BD=CE,∠ABE=∠ACD,BE与CD相交于点F.求证:△ABC是等腰三角形.
图4-15-15
温馨提示:此类考题常见于广东省中考数学试卷的第18题,分值一般为7分,答题时要注意书写格式,分步书写,慢做会求全对,评卷老师是分步给分的哦!
【典型错例】等腰三角形性质的综合运用漏解
2. 等腰三角形一腰上的高与另一腰的夹角为50°,求该等腰三角形顶角的度数.
解:①如答图4-15-2,当等腰三角形ABC为锐角三角形时,
∵∠ABD=50°,BD⊥AC,
∴∠A=90°-∠ABD=40°.
∴此时三角形的顶角为40°;
答图4-15-2
②如答图4-15-3,当等腰三角形ABC为钝角三角形时,
∵BD⊥AC,∴∠BDA=90°.
∵∠ABD=50°,∴∠BAC=∠ABD+∠BDA=140°.
∴此时三角形的顶角为140°.
综上所述,该等腰三角形顶角的度数为40°或140°.
答图4-15-3
错解分析
错解:如图4-15-16,在等腰三角形ABC中,AB=AC,BD为AC边上的高.
由题意知∠ABD=50°,
∴∠A=90°-∠ABD=40°. ∴该等腰三角形顶角的度数为40°.
剖析:该解答过程的错误在于直接默认等腰三角形是锐角三角形,忽视了还有钝角三角形的情况.本题要进行分类讨论,分等腰三角形的顶角是锐角和等腰三角形的顶角是钝角两种情况,再分别解答.
图4-15-16
【生长式训练】知识生长→变式创新
3. (中考创新,原创题)如图4-15-17,△ACB和△DCE均是顶角为40°的等腰三角形,AB,DE分别是底边,连接AD,BE,点A,D,E在同一直线上.
知识种子:基本概念
(1)填空:∠BAC= ,∠ADC= ;
图4-15-17
70°
110°
种子生长:等腰三角形的性质
(2)求证:AD=BE;
图4-15-17
生长变式:图形变式
(3)如图4-15-18,若△ACB和△DCE均是等边三角形,连接AD,BE,点A,D,E在同一直线上.
①求∠AEB的度数;
图4-15-18
①∵∠CDE=60°,点A,D,E在同一直线上,
∴∠ADC=180°-∠CDE=120°.
∴∠BEC=∠ADC =120°.
∵∠CED=60°,
∴∠AEB=∠BEC-∠CED=120°-60°=60°.
图4-15-18
②AE=BE+CE.
理由:∵AE=AD+DE,AD=BE,DE=CE,
∴AE=BE+CE.
图4-15-18
②求线段AE,BE,CE之间的数量关系,并说明理由;
种子成树:综合创新
(4)如图4-15-19,若△ACB和△DCE均为等腰直角三角形,∠ACB=∠DCE=90°,连接AD,BE,点A,D,E在同一直线上,CM为△DCE的边DE上的高.
图4-15-19
图4-15-19
①求∠AEB的度数;
②AE= BE+2CM.
理由:∵CM为△DCE的边DE上的高,∴CM⊥DE.
又∵CD=CE,∴DM=EM.
∵∠DCE=90°,∴DE=2CM.
∵AE=AD+DE,AD=BE,DE=2CM,∴AE=BE+2CM.
图4-15-19
中考演练
(限时15分钟)
一、选择题
1. (2024·青海)如图4-15-20,OC平分∠AOB,点P在OC上,PD⊥OB,PD=2,则点P到OA的距离是 ( )
A. 4 B. 3
C. 2 D. 1
图4-15-20
C
2. (2024·兰州)如图4-15-21,在△ABC中,AB=AC,∠BAC=130°,DA⊥AC,则∠ADB= ( )
A. 100° B. 115°
C. 130° D. 145°
B
图4-15-21
图4-15-22
A
4. (2024·凉山州)如图4-15-23,在Rt△ABC中,∠ACB=90°,DE垂直平分AB交BC于点D.若△ACD的周长为50 cm,则AC+BC= ( )
A. 25 cm B. 45 cm
C. 50 cm D. 55 cm
图4-15-23
C
图4-15-24
C
二、填空题
6. (2023·丽水)如图4-15-25,在△ABC中,AC的垂直平分线交BC于点D,交AC于点E,∠B=∠ADB. 若AB=4,则DC的长是 .
图4-15-25
4
7. (2024·重庆)如图4-15-26,在△ABC中,AB=AC,∠A=36°,BD平分∠ABC交AC于点D. 若BC=2,则AD的长度为 .
图4-15-26
2
8. (2023·随州)如图4-15-27,在Rt△ABC中,∠C=90°,AC=8,BC=6,D为AC上一点,若BD是∠ABC的平分线,则AD= .
图4-15-27
5
三、解答题
9. (2024·宜宾)如图4-15-28,D,E分别是等边三角形ABC边BC,AC上的点,且BD=CE,BE与AD交于点F. 求证:AD=BE.
图4-15-28
10. (2022·温州)如图4-15-29,BD是△ABC的角平分线,DE∥BC,交AB于点E.
(1)求证:∠EBD=∠EDB;
(1)证明:∵BD是△ABC的角平分线,∴∠CBD=∠EBD.
∵DE∥BC,∴∠CBD=∠EDB. ∴∠EBD=∠EDB.
图4-15-29
(2)当AB=AC时,请判断CD与ED的大小关系,并说明理由.
(2)解:CD=ED.
理由:∵AB=AC,∴∠ABC=∠C.
∵DE∥BC,∴∠ADE=∠C,∠AED=∠ABC. ∴∠ADE=∠AED.
∴AD=AE. ∴AC-AD=AB-AE,即CD=BE.
由(1)知∠EBD=∠EDB,∴BE=ED. ∴CD=ED.
图4-15-29
命题趋势
( 限时 5 分钟)
(教材改编)如图4-15-30,在△ABC中,DE是边BC的垂直平分线,分别交边AC,BC于点D,E,BF⊥AC,且F是线段AD的中点,延长BF与BC的垂直平分线交于点G,连接CG.
(1)若D是AC的中点,求证:AC=2AB;
证明:(1)如答图4-15-4,连接BD.
∵DE是边BC的垂直平分线,∴DB=DC.
∵BF⊥AC,F是AD的中点,∴AB=DB.
∴AB=DC.
又∵D是AC的中点,∴AC=2DC=2AB.
图4-15-30
答图4-15-4
(2)若∠ACB=30°,求证:△BGC为等边三角形.
(2)∵DE是边BC的垂直平分线,
∴BG=CG.
∴△BGC为等腰三角形.
∵BF⊥AC,∴∠BFC=90°.
∵∠ACB=30°,
∴∠GBC=90°-∠ACB=60°.
∴△BGC为等边三角形.
图4-15-30
命题解读:根据最新课程标准和近三年中考命题动向,预测2025年中考命题方向可能注重考查等腰三角形、等边三角形、直角三角形的基本概念、性质和判定方法;注重考查角平分线、垂直平分线的性质,可能会结合尺规作图一起考查;强调与其他知识点的综合考查,如与三角形的全等、相似、三角函数、圆等结合;还可能会结合实际生活情境进行考查.
同课章节目录
