中考数学复习知识梳理第四章三角形第16课时全等三角形课件(共44张PPT)
文档属性
| 名称 | 中考数学复习知识梳理第四章三角形第16课时全等三角形课件(共44张PPT) |

|
|
| 格式 | ppt | ||
| 文件大小 | 5.0MB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 通用版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2025-05-31 00:00:00 | ||
图片预览










文档简介
(共44张PPT)
第四章 三 角 形
第16课时 全等三角形
课前循环练
(限时5分钟)
1. (广东真题)如图4-16-1,四边形ABCD内接于☉O.若∠BOD=100°,则∠DAB的度数为 ( )
A. 50° B. 80°
C. 100° D. 130°
图4-16-1
D
C
B
图4-16-2
x+3
4
①理解全等三角形的概念,能识别全等三角形中的对应边、对应角.
②掌握基本事实:两边及其夹角分别相等的两个三角形全等.
③掌握基本事实:两角及其夹边分别相等的两个三角形全等.
④掌握基本事实:三边分别相等的两个三角形全等.
⑤证明定理:两角分别相等且其中一组等角的对边相等的两个三角形全等.
⑥探索并掌握判定直角三角形全等的“斜边、直角边”定理.
课标要求
对接教材 人教:八上第十二章 全等三角形
北师:七下第四章 三角形
考点梳理
考点复习
1.全等三角形的概念
能够 的两个三角形叫做全等三角形.把两个全等的三角形重合在一起,重合的顶点叫做对应点,重合的边叫做 ,重合的角叫做
完全重合
对应边
对应角
广东省对应考点例题
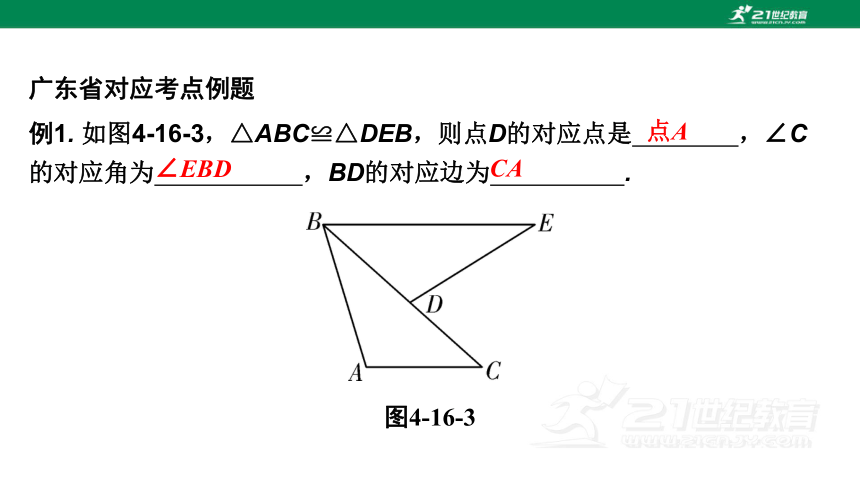
例1. 如图4-16-3,△ABC≌△DEB,则点D的对应点是 ,∠C的对应角为 ,BD的对应边为 .
图4-16-3
点A
∠EBD
CA
2.全等三角形的性质
全等三角形的 相等, 相等.全等三角形的对应线段(高、中线、角平分线)、周长、面积分别对应
例2. 若△ABC≌△DEF,且△ABC的周长为20,AB=5,BC=8,则DF的长为 ( )
A. 5 B. 8
C. 7 D. 5或8
对应边
对应角
相等
C
3.全等三角形的判定
已知条件 图形 判定方法
三边
SSS
两角
一边 两角
夹边
ASA
两角
对边
AAS
已知条件 图形 判定方法
两边
一角 两边
夹角 SAS
两边
对角
HL
不可判定
三角
不可判定
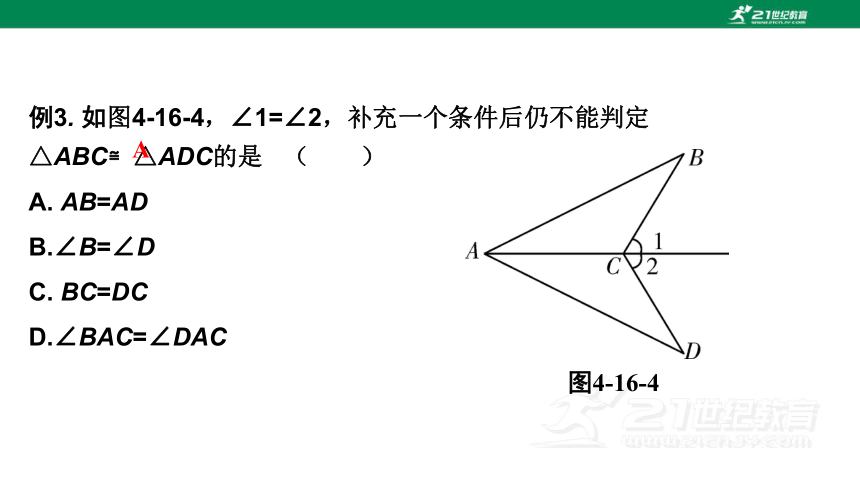
例3. 如图4-16-4,∠1=∠2,补充一个条件后仍不能判定△ABC≌△ADC的是 ( )
A. AB=AD
B.∠B=∠D
C. BC=DC
D.∠BAC=∠DAC
图4-16-4
A
广东中考
1. (2022·广东题18,8分,全等三角形的判定与性质;角平分线的性质)如图4-16-5,已知∠AOC=∠BOC,点P在OC上,PD⊥OA,PE⊥OB,垂足分别为D,E. 求证:△OPD≌△OPE.
图4-16-5
2. (2023·广东题23节选,3分,全等三角形的判定与性质;旋转的性质)综合运用
如图4-16-6①,在平面直角坐标系中,正方形OABC的顶点A在x轴的正半轴上. 如图4-16-6②,将正方形OABC绕点O逆时针旋转,旋转角为α(0°<α<45°),AB交直线y=x于点E,BC交y轴于点F. 当旋转角∠COF为多少度时,OE=OF.
图4-16-6
图4-16-6
高分击破
【典型考点】全等三角形的判定 得分点分析
1. (2022·广东改编)如图4-16-7,OC是∠AOB的平分线,P是OC上一点,PD⊥OA于点D,PE⊥OB于点E,
图4-16-7
(1)求证:OD=OE;
图4-16-7
(2)若F是OC上的不同于点P的任一点,连接DF,EF.求证:DF=EF.
图4-16-7
温馨提示:此类考题常见于广东省中考数学试卷的第19题,分值一般为9分,答题时要注意书写格式,分步书写,慢做会求全对,评卷老师是分步给分的哦!
【典型错例】全等三角形判定方法的错误运用——SSA或AAA
2. (教材改编)如图4-16-8,在△ABC中,已知AB=AC,D,E分别是AB,AC的中点,且CD=BE. 求证:△ADC≌△AEB.
图4-16-8
图4-16-8
【生长式训练】知识生长→变式创新
3. (中考创新,原创题)如图4-16-9,在平面直角坐标系中,点A,B的坐标分别为(-2,0),(0,3),C是x轴上一点,D是y轴上一点.
知识种子:基本概念
(1)若点C(2,0),且△COD≌△AOB,则点D的坐标为____________
;
图4-16-9
(0,3)或
(0,-3)
种子生长:全等三角形的判定与性质
(2)若点C(3,0),D(0,2),判断线段AB与CD的数量关系和位置关系,并说明理由;
答图4-16-1
∴△AOB≌△DOC(SAS).
∴∠BAO=∠CDO, AB=CD.
∵∠BDE=∠CDO,∴∠BDE=∠BAO.
∵∠AOB=90°,∴∠ABO +∠BAO=90°.
∴∠AEC=∠ABO +∠BDE=∠ABO +∠BAO=90°.
∴AB⊥CD.
答图4-16-1
生长变式:图形变式
(3)如图4-16-10,以AB为直角边在第二象限内作等腰直角三角形ABE,∠EAB=90°,求点E的坐标;
图4-16-10
解:如答图4-16-2,过点E作EF⊥x轴于点F,则∠EFA=90°.
∴∠AEF+∠FAE=90°.
∵∠EAB=90°,∴∠FAE+∠BAO=90°.
∴∠AEF=∠BAO.
∵△ABE是等腰直角三角形,∴AE=AB.
答图4-16-2
答图4-16-2
种子成树:综合创新
(4)如图4-16-11,若点A的坐标保持不变,B为y轴正半轴上一动点,以AB为直角边在右侧作等腰直角三角形ABQ,∠ABQ=90°,过点Q作QR⊥x轴于点R.当点B运动时,OB-QR的值是否发生变化?若不变,求出其值;若发生变化,请说明理由.
图4-16-11
解:不变.
如答图4-16-3,过点Q作QH⊥y轴于点H,
则∠BHQ=∠OHQ=90°.
∴∠HBQ+∠BQH=90°.
∵∠ABQ=90°,∴∠ABO+∠HBQ=90°.
∴∠ABO=∠BQH.
∵△ABQ是等腰直角三角形,∴AB=QB.
答图4-16-3
答图4-16-3
中考演练
(限时15分钟)
一、选择题
1. (2024·济南)如图4-16-12,已知△ABC≌△DEC,∠A=60°,∠B=
40°,则∠DCE的度数为 ( )
A. 40° B. 60°
C. 80° D. 100°
图4-16-12
C
2. (2023·甘孜州)如图4-16-13,AB与CD相交于点O,AC∥BD,只添加一个条件,能判定△AOC≌△BOD的是 ( )
A. ∠A=∠D
B. AO=BO
C. AC=BO
D. AB=CD
图4-16-13
B
3. (2023·凉山州)如图4-16-14,点E,F在BC上,BE=CF,∠B=∠C,添加一个条件,不能证明△ABF≌△DCE的是 ( )
A. ∠A=∠D
B. ∠AFB=∠DEC
C. AB=DC
D. AF=DE
图4-16-14
D
4. (2023·长春)如图4-16-15,工人师傅设计了一种测零件内径AB的卡钳,卡钳交叉点O为AA',BB'的中点,只要量出A'B'的长度,就可以知道该零件内径AB的长度. 依据的数学基本事实是 ( )
A. 两边及其夹角分别相等的两个三角形全等
B. 两角及其夹边分别相等的两个三角形全等
C. 两条直线被一组平行线所截,所得的对应线段成比例
D. 两点之间线段最短
图4-16-15
A
5. (2024·安徽)在凸五边形ABCDE中,AB=AE,BC=DE,F是CD的中点. 下列条件中,不能推出AF与CD一定垂直的是 ( )
A. ∠ABC=∠AED
B. ∠BAF=∠EAF
C. ∠BCF=∠EDF
D. ∠ABD=∠AEC
D
二、填空题
6. (2023·成都)如图4-16-16,已知△ABC≌△DEF,点B,E,C,F依次在同一条直线上. 若BC=8,CE=5,则CF的长为 .
图4-16-16
3
7. (2024·成都)如图4-16-17,△ABC≌△CDE,若∠D=35°,∠ACB=
45°,则∠DCE的度数为 .
100°
图4-16-17
8. (2024·牡丹江)如图4-16-18,△ABC中,D是AB上一点,CF∥AB,D,E,F三点共线,请添加一个条件 ,使得AE=CE. (只添一种情况即可)
图4-16-18
DE=EF(答案不唯一)
三、解答题
9. (2024·云南)如图4-16-19,在△ABC和△AED中,AB=AE,∠BAE=∠CAD,AC=AD. 求证:△ABC≌△AED.
图4-16-19
10. (2024·长沙)如图4-16-20,点C在线段AD上,AB=AD,∠B=∠D,BC=DE.
(1)求证:△ABC≌△ADE;
图4-16-20
(2)若∠BAC=60°,求∠ACE的度数.
(2)解:∵△ABC≌△ADE,∠BAC=60°,
∴AC=AE,∠DAE=∠BAC=60°.
∴△ACE是等边三角形.
∴∠ACE=60°.
图4-16-20
命题趋势
( 限时 5 分钟)
(综合探究)【问题背景】
如图4-16-21,在△ABC中,AC=BC,D是BC的中点,E是AC的中点,连接AD,BE.
图4-16-21
图4-16-21
【数学理解】
(1)如图4-16-21①,求证:AD=BE;
【拓展探索】
(2)如图4-16-21②,若∠ACB=90°,分别延长BE,DA到点F,G,使BF=2BE,DG=2DA,连接AF,FG,则线段AG与线段FG相等吗?请说明理由.
图4-16-21
答图4-16-4
命题解读:根据最新课程标准和近三年中考命题动向,预测2025年中考命题方向可能注重考查全等三角形的基本概念、性质和判定方法,如通过具体图形判断三角形全等的条件、利用全等三角形的判定方法进行证明、利用全等三角形的性质进行计算等;强调与其他几何知识的综合运用,可能与特殊四边形、圆等结合;还可能会考查综合探究类题型,通过变换图形位置或构造特殊图形综合考查.
第四章 三 角 形
第16课时 全等三角形
课前循环练
(限时5分钟)
1. (广东真题)如图4-16-1,四边形ABCD内接于☉O.若∠BOD=100°,则∠DAB的度数为 ( )
A. 50° B. 80°
C. 100° D. 130°
图4-16-1
D
C
B
图4-16-2
x+3
4
①理解全等三角形的概念,能识别全等三角形中的对应边、对应角.
②掌握基本事实:两边及其夹角分别相等的两个三角形全等.
③掌握基本事实:两角及其夹边分别相等的两个三角形全等.
④掌握基本事实:三边分别相等的两个三角形全等.
⑤证明定理:两角分别相等且其中一组等角的对边相等的两个三角形全等.
⑥探索并掌握判定直角三角形全等的“斜边、直角边”定理.
课标要求
对接教材 人教:八上第十二章 全等三角形
北师:七下第四章 三角形
考点梳理
考点复习
1.全等三角形的概念
能够 的两个三角形叫做全等三角形.把两个全等的三角形重合在一起,重合的顶点叫做对应点,重合的边叫做 ,重合的角叫做
完全重合
对应边
对应角
广东省对应考点例题
例1. 如图4-16-3,△ABC≌△DEB,则点D的对应点是 ,∠C的对应角为 ,BD的对应边为 .
图4-16-3
点A
∠EBD
CA
2.全等三角形的性质
全等三角形的 相等, 相等.全等三角形的对应线段(高、中线、角平分线)、周长、面积分别对应
例2. 若△ABC≌△DEF,且△ABC的周长为20,AB=5,BC=8,则DF的长为 ( )
A. 5 B. 8
C. 7 D. 5或8
对应边
对应角
相等
C
3.全等三角形的判定
已知条件 图形 判定方法
三边
SSS
两角
一边 两角
夹边
ASA
两角
对边
AAS
已知条件 图形 判定方法
两边
一角 两边
夹角 SAS
两边
对角
HL
不可判定
三角
不可判定
例3. 如图4-16-4,∠1=∠2,补充一个条件后仍不能判定△ABC≌△ADC的是 ( )
A. AB=AD
B.∠B=∠D
C. BC=DC
D.∠BAC=∠DAC
图4-16-4
A
广东中考
1. (2022·广东题18,8分,全等三角形的判定与性质;角平分线的性质)如图4-16-5,已知∠AOC=∠BOC,点P在OC上,PD⊥OA,PE⊥OB,垂足分别为D,E. 求证:△OPD≌△OPE.
图4-16-5
2. (2023·广东题23节选,3分,全等三角形的判定与性质;旋转的性质)综合运用
如图4-16-6①,在平面直角坐标系中,正方形OABC的顶点A在x轴的正半轴上. 如图4-16-6②,将正方形OABC绕点O逆时针旋转,旋转角为α(0°<α<45°),AB交直线y=x于点E,BC交y轴于点F. 当旋转角∠COF为多少度时,OE=OF.
图4-16-6
图4-16-6
高分击破
【典型考点】全等三角形的判定 得分点分析
1. (2022·广东改编)如图4-16-7,OC是∠AOB的平分线,P是OC上一点,PD⊥OA于点D,PE⊥OB于点E,
图4-16-7
(1)求证:OD=OE;
图4-16-7
(2)若F是OC上的不同于点P的任一点,连接DF,EF.求证:DF=EF.
图4-16-7
温馨提示:此类考题常见于广东省中考数学试卷的第19题,分值一般为9分,答题时要注意书写格式,分步书写,慢做会求全对,评卷老师是分步给分的哦!
【典型错例】全等三角形判定方法的错误运用——SSA或AAA
2. (教材改编)如图4-16-8,在△ABC中,已知AB=AC,D,E分别是AB,AC的中点,且CD=BE. 求证:△ADC≌△AEB.
图4-16-8
图4-16-8
【生长式训练】知识生长→变式创新
3. (中考创新,原创题)如图4-16-9,在平面直角坐标系中,点A,B的坐标分别为(-2,0),(0,3),C是x轴上一点,D是y轴上一点.
知识种子:基本概念
(1)若点C(2,0),且△COD≌△AOB,则点D的坐标为____________
;
图4-16-9
(0,3)或
(0,-3)
种子生长:全等三角形的判定与性质
(2)若点C(3,0),D(0,2),判断线段AB与CD的数量关系和位置关系,并说明理由;
答图4-16-1
∴△AOB≌△DOC(SAS).
∴∠BAO=∠CDO, AB=CD.
∵∠BDE=∠CDO,∴∠BDE=∠BAO.
∵∠AOB=90°,∴∠ABO +∠BAO=90°.
∴∠AEC=∠ABO +∠BDE=∠ABO +∠BAO=90°.
∴AB⊥CD.
答图4-16-1
生长变式:图形变式
(3)如图4-16-10,以AB为直角边在第二象限内作等腰直角三角形ABE,∠EAB=90°,求点E的坐标;
图4-16-10
解:如答图4-16-2,过点E作EF⊥x轴于点F,则∠EFA=90°.
∴∠AEF+∠FAE=90°.
∵∠EAB=90°,∴∠FAE+∠BAO=90°.
∴∠AEF=∠BAO.
∵△ABE是等腰直角三角形,∴AE=AB.
答图4-16-2
答图4-16-2
种子成树:综合创新
(4)如图4-16-11,若点A的坐标保持不变,B为y轴正半轴上一动点,以AB为直角边在右侧作等腰直角三角形ABQ,∠ABQ=90°,过点Q作QR⊥x轴于点R.当点B运动时,OB-QR的值是否发生变化?若不变,求出其值;若发生变化,请说明理由.
图4-16-11
解:不变.
如答图4-16-3,过点Q作QH⊥y轴于点H,
则∠BHQ=∠OHQ=90°.
∴∠HBQ+∠BQH=90°.
∵∠ABQ=90°,∴∠ABO+∠HBQ=90°.
∴∠ABO=∠BQH.
∵△ABQ是等腰直角三角形,∴AB=QB.
答图4-16-3
答图4-16-3
中考演练
(限时15分钟)
一、选择题
1. (2024·济南)如图4-16-12,已知△ABC≌△DEC,∠A=60°,∠B=
40°,则∠DCE的度数为 ( )
A. 40° B. 60°
C. 80° D. 100°
图4-16-12
C
2. (2023·甘孜州)如图4-16-13,AB与CD相交于点O,AC∥BD,只添加一个条件,能判定△AOC≌△BOD的是 ( )
A. ∠A=∠D
B. AO=BO
C. AC=BO
D. AB=CD
图4-16-13
B
3. (2023·凉山州)如图4-16-14,点E,F在BC上,BE=CF,∠B=∠C,添加一个条件,不能证明△ABF≌△DCE的是 ( )
A. ∠A=∠D
B. ∠AFB=∠DEC
C. AB=DC
D. AF=DE
图4-16-14
D
4. (2023·长春)如图4-16-15,工人师傅设计了一种测零件内径AB的卡钳,卡钳交叉点O为AA',BB'的中点,只要量出A'B'的长度,就可以知道该零件内径AB的长度. 依据的数学基本事实是 ( )
A. 两边及其夹角分别相等的两个三角形全等
B. 两角及其夹边分别相等的两个三角形全等
C. 两条直线被一组平行线所截,所得的对应线段成比例
D. 两点之间线段最短
图4-16-15
A
5. (2024·安徽)在凸五边形ABCDE中,AB=AE,BC=DE,F是CD的中点. 下列条件中,不能推出AF与CD一定垂直的是 ( )
A. ∠ABC=∠AED
B. ∠BAF=∠EAF
C. ∠BCF=∠EDF
D. ∠ABD=∠AEC
D
二、填空题
6. (2023·成都)如图4-16-16,已知△ABC≌△DEF,点B,E,C,F依次在同一条直线上. 若BC=8,CE=5,则CF的长为 .
图4-16-16
3
7. (2024·成都)如图4-16-17,△ABC≌△CDE,若∠D=35°,∠ACB=
45°,则∠DCE的度数为 .
100°
图4-16-17
8. (2024·牡丹江)如图4-16-18,△ABC中,D是AB上一点,CF∥AB,D,E,F三点共线,请添加一个条件 ,使得AE=CE. (只添一种情况即可)
图4-16-18
DE=EF(答案不唯一)
三、解答题
9. (2024·云南)如图4-16-19,在△ABC和△AED中,AB=AE,∠BAE=∠CAD,AC=AD. 求证:△ABC≌△AED.
图4-16-19
10. (2024·长沙)如图4-16-20,点C在线段AD上,AB=AD,∠B=∠D,BC=DE.
(1)求证:△ABC≌△ADE;
图4-16-20
(2)若∠BAC=60°,求∠ACE的度数.
(2)解:∵△ABC≌△ADE,∠BAC=60°,
∴AC=AE,∠DAE=∠BAC=60°.
∴△ACE是等边三角形.
∴∠ACE=60°.
图4-16-20
命题趋势
( 限时 5 分钟)
(综合探究)【问题背景】
如图4-16-21,在△ABC中,AC=BC,D是BC的中点,E是AC的中点,连接AD,BE.
图4-16-21
图4-16-21
【数学理解】
(1)如图4-16-21①,求证:AD=BE;
【拓展探索】
(2)如图4-16-21②,若∠ACB=90°,分别延长BE,DA到点F,G,使BF=2BE,DG=2DA,连接AF,FG,则线段AG与线段FG相等吗?请说明理由.
图4-16-21
答图4-16-4
命题解读:根据最新课程标准和近三年中考命题动向,预测2025年中考命题方向可能注重考查全等三角形的基本概念、性质和判定方法,如通过具体图形判断三角形全等的条件、利用全等三角形的判定方法进行证明、利用全等三角形的性质进行计算等;强调与其他几何知识的综合运用,可能与特殊四边形、圆等结合;还可能会考查综合探究类题型,通过变换图形位置或构造特殊图形综合考查.
同课章节目录
