中考数学复习知识梳理第四章三角形第18课时锐角三角函数与解直角三角形课件(共54张PPT)
文档属性
| 名称 | 中考数学复习知识梳理第四章三角形第18课时锐角三角函数与解直角三角形课件(共54张PPT) |  | |
| 格式 | ppt | ||
| 文件大小 | 10.6MB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 通用版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2025-05-31 09:30:19 | ||
图片预览










文档简介
(共54张PPT)
第四章 三 角 形
第18课时 锐角三角函数与解直角三角形
课前循环练
(限时5分钟)
1. (广东真题)化简a4·a2+(a3)2的结果是 ( )
A. a8+a6 B. a6+a9 C. 2a6 D. a12
2. (广东真题)已知OP=5,☉O的半径为5,则点P在 ( )
A. ☉O上 B. ☉O内 C. ☉O外 D. 圆心上
C
A
3. (广东真题)已知y是x的函数,y与x-1成正比例,如果这个函数的图象经过点(a,a)(a≠0),那么它的图象大致是 ( )
B
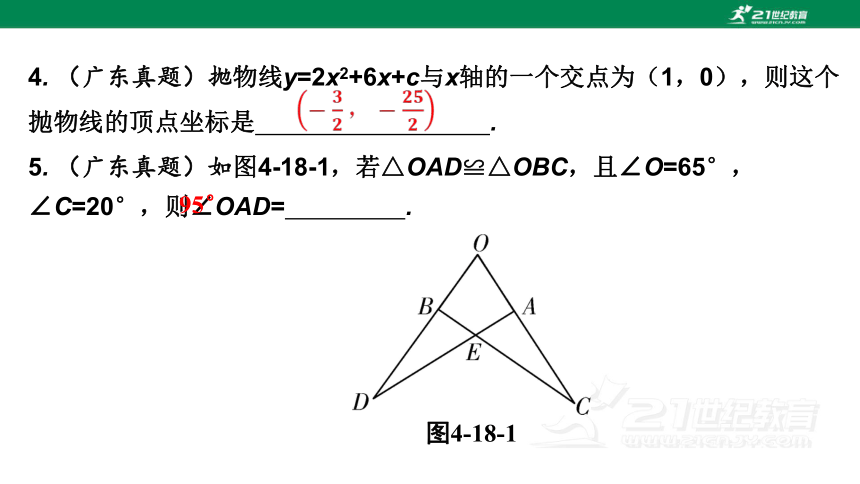
4. (广东真题)抛物线y=2x2+6x+c与x轴的一个交点为(1,0),则这个
抛物线的顶点坐标是 .
5. (广东真题)如图4-18-1,若△OAD≌△OBC,且∠O=65°,∠C=20°,则∠OAD= .
图4-18-1
95°
①利用相似的直角三角形,探索并认识锐角三角函数(sin A,cos A,tan A),知道30°,45°,60°角的三角函数值.
②会使用计算器由已知锐角求它的三角函数值,由已知三角函数值求它的对应锐角.
③能用锐角三角函数解直角三角形,能用相关知识解决一些简单的实际问题.
课标要求
对接教材 人教:九下第二十八章 锐角三角函数
北师:九下第一章 直角三角形的边角关系
考点梳理
考点复习
1.特殊角的三角函数值
锐角三角函数 角α
30° 45° 60°
sin α
cos α
tan α
1
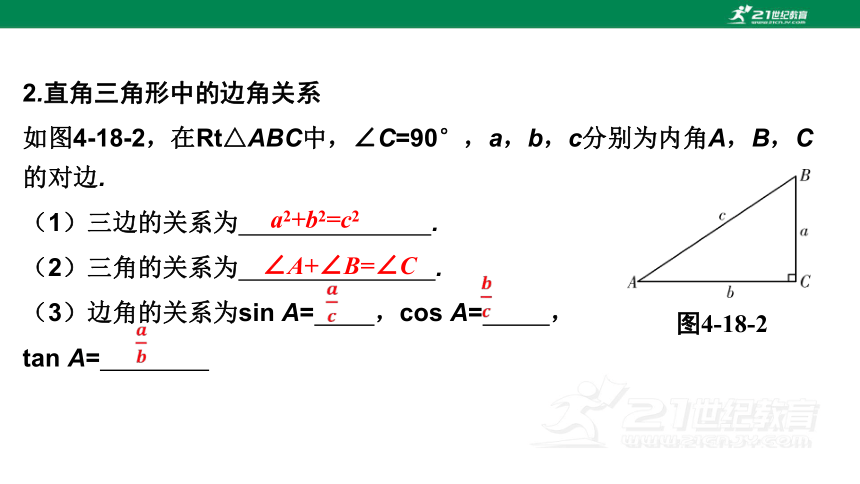
2.直角三角形中的边角关系
如图4-18-2,在Rt△ABC中,∠C=90°,a,b,c分别为内角A,B,C的对边.
(1)三边的关系为 .
(2)三角的关系为 .
(3)边角的关系为sin A= ,cos A= ,
tan A=
图4-18-2
a2+b2=c2
∠A+∠B=∠C
例2. 如图4-18-3,在△ABC中,∠C=90°,AC=4,BC=3,则tan A= ,sin A= ,cos A= .
图4-18-3
3.解直角三角形
在直角三角形的六个元素中,除直角外,只要再知道 (其中至少有一个是 ),就可以求出其余三个未知元素.
解直角三角形的基本类型可分为以下几种情况(如图4-18-2):
两个元素
边
已知条件 解法
一条
边和
一个
锐角 斜边c和
锐角∠A ∠B= ,
a= ,
b=
直角边a
和锐角∠A ∠B= ,
b= ,
c=
90°-∠A
c·sin A
90°-∠A
c·cos A
已知条件 解法
两
条
边 两条直角
边a和b c= ,
由 求∠A,
∠B=
直角边a
和斜边c b= ,
由 求∠A,
∠B=
90°-∠A
90°-∠A
例3.在Rt△ABC中,∠C=90°,∠A,∠B,∠C的对边分别为a,b,c,根据下列条件解直角三角形.
(1)c=30,∠A=60°; (2)b=5,c=10.
4.解直角三角形的应用
(1)仰角、俯角
如图4-18-4,在视线与水平线所成的角中,视线在水平线上方的是
,视线在水平线下方的是 .
图4-18-4
仰角
俯角
(2)方位角
如图4-18-5,从正北方向线或正南方向线到目标方向线所成的小于90°的角(如α,β),叫做方位角.
图4-18-5
图4-18-6
坡角
tan α
例4. (1)如图4-18-7,从航拍无人机A看一栋楼顶部B的仰角α为30°,看这栋楼底部C的俯角β为60°,无人机与楼的水平距离为60 m,则这栋楼的高度为 m;
图4-18-7
(2)如图4-18-8,湖中有一个小岛A,一艘轮船由西向东航行,它在B处测得小岛A在北偏东60°方向上,航行20 n mile到达C处,这时测得小岛A在北偏东30°方向上,则小岛A到航线BC的距离为 n mile;
图4-18-8
图4-18-9
20
广东中考
图4-18-10
3. (2023·广东题18,7分,解直角三角形的应用)2023年5月30日,神舟十六号载人飞船发射取得圆满成功,3名航天员顺利进驻中国空间站. 如图4-18-11,照片展示了中国空间站上机械臂的一种工作状态. 当两臂AC=BC=10 m,两臂夹角∠ACB=100°时,求A,B两点间的距离. (结果精确到0.1 m,参考数据:sin 50°≈0.766,cos 50°≈0.643,tan 50°≈
1.192)
图4-18-11
答图4-18-1
图4-18-12
(1)求PQ的长;
图4-18-12
图4-18-12
(2)该充电站有20个停车位,求PN的长.
图4-18-12
高分击破
【典型考点】解直角三角形的应用 得分点分析
1. (2023·丽水)如图4-18-13,某工厂为了提升生产过程中所产生废气的净化效率,需在气体净化设备上增加一条管道A-D-C,已知DC⊥BC,AB⊥BC,∠A=60°,AB=11 m,CD=4 m,求管道A-D-C的总长.
图4-18-13
图4-18-14
温馨提示:此类考题常见于广东省中考数学试卷的第18小题,分值一般为7分,答题时要注意书写格式,分步书写,慢做会求全对,评卷老师是分步给分的哦!
图4-18-15
B
错解分析
错解:由题意,得∠BAC=α.
在Rt△ABC中,AC=a m,
∴BC=AC·tan∠BAC=a·tan α(m).
故选A.
剖析:上面的解答过程没有理解俯角的概念,误认为∠BAC为从A处测得目标B处的俯角α,从而导致出错.
【生长式训练】知识生长→变式创新
3. (中考创新,原创题)如图4-18-16,在△ABC中,AC=6.
知识种子:基本概念
(1)若∠A=90°,AB=8,则sin B= ;cos B= ;
tan B= ;
图4-18-16
种子生长:解直角三角形
(2)如图4-18-17,若∠B=45°,∠C=75°,求BC的长;
图4-18-17
解:如答图4-18-2,过点C作CD⊥AB于点D.
∵∠B=45°,
∴∠BCD=90°-∠B=45°.
∵∠ACB=75°,
∴∠ACD=∠ACB -∠BCD=30°.
答图4-18-2
答图4-18-2
生长变式:图形变式
(3)如图4-18-18,若∠B=45°,∠C=60°,求BC的长;
图4-18-18
答图4-18-3
图4-18-19
答图4-18-4
中考演练
(限时15分钟)
图4-18-20
C
图4-18-21
B
图4-18-22
A
图4-18-23
D
图4-18-24
A
二、填空题
6. (2024·绥化)如图4-18-25,用热气球的探测器测一栋楼的高度,从热气球上的点A测得该楼顶部点C的仰角为60°,测得底部点B的俯角为45°,点A与楼BC的水平距离AD=50 m,则这栋楼的高度为___________m.(结果保留根号)
图4-18-25
7. (2024·盐城)如图4-18-26,小明用无人机测量教学楼的高度,将无人机垂直上升距地面30 m的点P处,测得教学楼底端点A的俯角为37°,再将无人机沿教学楼方向水平飞行26.6 m至点Q处,测得教学楼顶端点B的俯角为45°,则教学楼AB的高度约为 m. (结果精确到1 m,参考数据:sin 37°≈0.60,cos 37°≈0.80,tan 37°≈0.75)
图4-18-26
17
8. (2024·眉山)如图4-18-27,斜坡CD的坡度i=1∶2,在斜坡上有一棵垂直于水平面的大树AB,当太阳光与水平面的夹角为60°时,大树在斜坡上的影子BE长为10 m,则大树AB的高为 m.
图4-18-27
三、解答题
9. (2023·成都)为建设美好公园社区,增强民众生活幸福感,某社区服务中心在文化活动室墙外安装遮阳篷,便于社区居民休憩.如图4-18-28,在侧面示意图中,遮阳篷AB长为5 m,与水平面的夹角为16°,且靠墙端离地高BC为4 m,当太阳光线AD与地面CE的夹角为45°时,求阴影CD的长.(结果精确到0.1 m,参考数据:sin 16°≈0.28,cos 16°≈0.96,tan 16°≈0.29)
图4-18-28
答图4-18-5
10. (2024·广州)2024年6月2日,嫦娥六号着陆器和上升器组合体(简称为“着上组合体”)成功着陆在月球背面. 某校综合实践小组制作了一个“着上组合体”的模拟装置,在一次试验中,如图4-18-29,该模拟装置在缓速下降阶段从点A垂直下降到点B,再垂直下降到着陆点C,从点B测得地面点D的俯角为36.87°,AD=17 m,BD=10 m.
图4-18-29
(1)求CD的长;
解:(1)如答图4-18-6,过点B作BE∥CD,
交AD于点E,
则∠BDC=∠EBD=36.87°.
在Rt△BCD中,BD=10 m,∠BDC=36.87°,
∴CD=BD·cos∠BDC=10×cos 36.87°≈8(m).
答图4-18-6
(2)若模拟装置从点A以每秒2 m的速度匀速下降到点B,求模拟装置从点A下降到点B的时间.
(参考数据:sin 36.87°≈0.60,cos 36.87°≈0.80,tan 36.87°≈0.75)
图4-18-29
命题趋势
( 限时 5 分钟)
(2024·广东改编)为解决停车问题,某小区在一段道路边的矩形空地上开辟一段斜列式停车位,如图4-18-30所示的矩形PQMN是该空地的平面示意图,所有停车位的形状、大小都相同, AFCQ是其中的一个停车位,每个停车位均有长5.5 m、宽2.5 m的矩形区域如矩形ABCD供停车,且∠AFC=60°.
图4-18-30
图4-18-30
(2)若矩形空地的长QM=60 m,则该空地最多可容纳多少个停车位?
答图4-18-7
命题解读:根据最新课程标准和近三年中考命题动向,预测2025年中考命题方向可能注重考查锐角三角函数的基本概念和特殊角的三角函数值;强调解直角三角形在实际问题中的应用,可能会结合科技情境、生活情境或社会情境进行考查,也可能结合建筑、测量、航海等考查仰角和俯角、方位角、坡度和坡角等相关问题.
第四章 三 角 形
第18课时 锐角三角函数与解直角三角形
课前循环练
(限时5分钟)
1. (广东真题)化简a4·a2+(a3)2的结果是 ( )
A. a8+a6 B. a6+a9 C. 2a6 D. a12
2. (广东真题)已知OP=5,☉O的半径为5,则点P在 ( )
A. ☉O上 B. ☉O内 C. ☉O外 D. 圆心上
C
A
3. (广东真题)已知y是x的函数,y与x-1成正比例,如果这个函数的图象经过点(a,a)(a≠0),那么它的图象大致是 ( )
B
4. (广东真题)抛物线y=2x2+6x+c与x轴的一个交点为(1,0),则这个
抛物线的顶点坐标是 .
5. (广东真题)如图4-18-1,若△OAD≌△OBC,且∠O=65°,∠C=20°,则∠OAD= .
图4-18-1
95°
①利用相似的直角三角形,探索并认识锐角三角函数(sin A,cos A,tan A),知道30°,45°,60°角的三角函数值.
②会使用计算器由已知锐角求它的三角函数值,由已知三角函数值求它的对应锐角.
③能用锐角三角函数解直角三角形,能用相关知识解决一些简单的实际问题.
课标要求
对接教材 人教:九下第二十八章 锐角三角函数
北师:九下第一章 直角三角形的边角关系
考点梳理
考点复习
1.特殊角的三角函数值
锐角三角函数 角α
30° 45° 60°
sin α
cos α
tan α
1
2.直角三角形中的边角关系
如图4-18-2,在Rt△ABC中,∠C=90°,a,b,c分别为内角A,B,C的对边.
(1)三边的关系为 .
(2)三角的关系为 .
(3)边角的关系为sin A= ,cos A= ,
tan A=
图4-18-2
a2+b2=c2
∠A+∠B=∠C
例2. 如图4-18-3,在△ABC中,∠C=90°,AC=4,BC=3,则tan A= ,sin A= ,cos A= .
图4-18-3
3.解直角三角形
在直角三角形的六个元素中,除直角外,只要再知道 (其中至少有一个是 ),就可以求出其余三个未知元素.
解直角三角形的基本类型可分为以下几种情况(如图4-18-2):
两个元素
边
已知条件 解法
一条
边和
一个
锐角 斜边c和
锐角∠A ∠B= ,
a= ,
b=
直角边a
和锐角∠A ∠B= ,
b= ,
c=
90°-∠A
c·sin A
90°-∠A
c·cos A
已知条件 解法
两
条
边 两条直角
边a和b c= ,
由 求∠A,
∠B=
直角边a
和斜边c b= ,
由 求∠A,
∠B=
90°-∠A
90°-∠A
例3.在Rt△ABC中,∠C=90°,∠A,∠B,∠C的对边分别为a,b,c,根据下列条件解直角三角形.
(1)c=30,∠A=60°; (2)b=5,c=10.
4.解直角三角形的应用
(1)仰角、俯角
如图4-18-4,在视线与水平线所成的角中,视线在水平线上方的是
,视线在水平线下方的是 .
图4-18-4
仰角
俯角
(2)方位角
如图4-18-5,从正北方向线或正南方向线到目标方向线所成的小于90°的角(如α,β),叫做方位角.
图4-18-5
图4-18-6
坡角
tan α
例4. (1)如图4-18-7,从航拍无人机A看一栋楼顶部B的仰角α为30°,看这栋楼底部C的俯角β为60°,无人机与楼的水平距离为60 m,则这栋楼的高度为 m;
图4-18-7
(2)如图4-18-8,湖中有一个小岛A,一艘轮船由西向东航行,它在B处测得小岛A在北偏东60°方向上,航行20 n mile到达C处,这时测得小岛A在北偏东30°方向上,则小岛A到航线BC的距离为 n mile;
图4-18-8
图4-18-9
20
广东中考
图4-18-10
3. (2023·广东题18,7分,解直角三角形的应用)2023年5月30日,神舟十六号载人飞船发射取得圆满成功,3名航天员顺利进驻中国空间站. 如图4-18-11,照片展示了中国空间站上机械臂的一种工作状态. 当两臂AC=BC=10 m,两臂夹角∠ACB=100°时,求A,B两点间的距离. (结果精确到0.1 m,参考数据:sin 50°≈0.766,cos 50°≈0.643,tan 50°≈
1.192)
图4-18-11
答图4-18-1
图4-18-12
(1)求PQ的长;
图4-18-12
图4-18-12
(2)该充电站有20个停车位,求PN的长.
图4-18-12
高分击破
【典型考点】解直角三角形的应用 得分点分析
1. (2023·丽水)如图4-18-13,某工厂为了提升生产过程中所产生废气的净化效率,需在气体净化设备上增加一条管道A-D-C,已知DC⊥BC,AB⊥BC,∠A=60°,AB=11 m,CD=4 m,求管道A-D-C的总长.
图4-18-13
图4-18-14
温馨提示:此类考题常见于广东省中考数学试卷的第18小题,分值一般为7分,答题时要注意书写格式,分步书写,慢做会求全对,评卷老师是分步给分的哦!
图4-18-15
B
错解分析
错解:由题意,得∠BAC=α.
在Rt△ABC中,AC=a m,
∴BC=AC·tan∠BAC=a·tan α(m).
故选A.
剖析:上面的解答过程没有理解俯角的概念,误认为∠BAC为从A处测得目标B处的俯角α,从而导致出错.
【生长式训练】知识生长→变式创新
3. (中考创新,原创题)如图4-18-16,在△ABC中,AC=6.
知识种子:基本概念
(1)若∠A=90°,AB=8,则sin B= ;cos B= ;
tan B= ;
图4-18-16
种子生长:解直角三角形
(2)如图4-18-17,若∠B=45°,∠C=75°,求BC的长;
图4-18-17
解:如答图4-18-2,过点C作CD⊥AB于点D.
∵∠B=45°,
∴∠BCD=90°-∠B=45°.
∵∠ACB=75°,
∴∠ACD=∠ACB -∠BCD=30°.
答图4-18-2
答图4-18-2
生长变式:图形变式
(3)如图4-18-18,若∠B=45°,∠C=60°,求BC的长;
图4-18-18
答图4-18-3
图4-18-19
答图4-18-4
中考演练
(限时15分钟)
图4-18-20
C
图4-18-21
B
图4-18-22
A
图4-18-23
D
图4-18-24
A
二、填空题
6. (2024·绥化)如图4-18-25,用热气球的探测器测一栋楼的高度,从热气球上的点A测得该楼顶部点C的仰角为60°,测得底部点B的俯角为45°,点A与楼BC的水平距离AD=50 m,则这栋楼的高度为___________m.(结果保留根号)
图4-18-25
7. (2024·盐城)如图4-18-26,小明用无人机测量教学楼的高度,将无人机垂直上升距地面30 m的点P处,测得教学楼底端点A的俯角为37°,再将无人机沿教学楼方向水平飞行26.6 m至点Q处,测得教学楼顶端点B的俯角为45°,则教学楼AB的高度约为 m. (结果精确到1 m,参考数据:sin 37°≈0.60,cos 37°≈0.80,tan 37°≈0.75)
图4-18-26
17
8. (2024·眉山)如图4-18-27,斜坡CD的坡度i=1∶2,在斜坡上有一棵垂直于水平面的大树AB,当太阳光与水平面的夹角为60°时,大树在斜坡上的影子BE长为10 m,则大树AB的高为 m.
图4-18-27
三、解答题
9. (2023·成都)为建设美好公园社区,增强民众生活幸福感,某社区服务中心在文化活动室墙外安装遮阳篷,便于社区居民休憩.如图4-18-28,在侧面示意图中,遮阳篷AB长为5 m,与水平面的夹角为16°,且靠墙端离地高BC为4 m,当太阳光线AD与地面CE的夹角为45°时,求阴影CD的长.(结果精确到0.1 m,参考数据:sin 16°≈0.28,cos 16°≈0.96,tan 16°≈0.29)
图4-18-28
答图4-18-5
10. (2024·广州)2024年6月2日,嫦娥六号着陆器和上升器组合体(简称为“着上组合体”)成功着陆在月球背面. 某校综合实践小组制作了一个“着上组合体”的模拟装置,在一次试验中,如图4-18-29,该模拟装置在缓速下降阶段从点A垂直下降到点B,再垂直下降到着陆点C,从点B测得地面点D的俯角为36.87°,AD=17 m,BD=10 m.
图4-18-29
(1)求CD的长;
解:(1)如答图4-18-6,过点B作BE∥CD,
交AD于点E,
则∠BDC=∠EBD=36.87°.
在Rt△BCD中,BD=10 m,∠BDC=36.87°,
∴CD=BD·cos∠BDC=10×cos 36.87°≈8(m).
答图4-18-6
(2)若模拟装置从点A以每秒2 m的速度匀速下降到点B,求模拟装置从点A下降到点B的时间.
(参考数据:sin 36.87°≈0.60,cos 36.87°≈0.80,tan 36.87°≈0.75)
图4-18-29
命题趋势
( 限时 5 分钟)
(2024·广东改编)为解决停车问题,某小区在一段道路边的矩形空地上开辟一段斜列式停车位,如图4-18-30所示的矩形PQMN是该空地的平面示意图,所有停车位的形状、大小都相同, AFCQ是其中的一个停车位,每个停车位均有长5.5 m、宽2.5 m的矩形区域如矩形ABCD供停车,且∠AFC=60°.
图4-18-30
图4-18-30
(2)若矩形空地的长QM=60 m,则该空地最多可容纳多少个停车位?
答图4-18-7
命题解读:根据最新课程标准和近三年中考命题动向,预测2025年中考命题方向可能注重考查锐角三角函数的基本概念和特殊角的三角函数值;强调解直角三角形在实际问题中的应用,可能会结合科技情境、生活情境或社会情境进行考查,也可能结合建筑、测量、航海等考查仰角和俯角、方位角、坡度和坡角等相关问题.
同课章节目录
