中考数学复习知识梳理第四章三角形第13课时线、角、相交线与平行线课件(共54张PPT)
文档属性
| 名称 | 中考数学复习知识梳理第四章三角形第13课时线、角、相交线与平行线课件(共54张PPT) |  | |
| 格式 | ppt | ||
| 文件大小 | 4.1MB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 通用版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2025-05-31 09:32:48 | ||
图片预览









文档简介
(共54张PPT)
第四章 三 角 形
第13课时 线、角、相交线与平行线
课前循环练
(限时5分钟)
1. (广东真题)下列式子是完全平方式的是 ( )
A. a2+ab+b2 B. a2+2a+2
C. a2-2b+b2 D. a2+2a+1
D
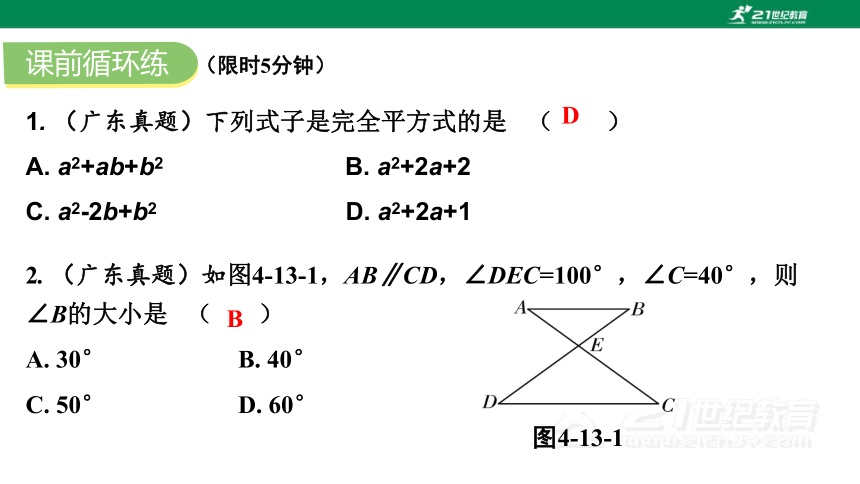
2. (广东真题)如图4-13-1,AB∥CD,∠DEC=100°,∠C=40°,则∠B的大小是 ( )
A. 30° B. 40°
C. 50° D. 60°
图4-13-1
B
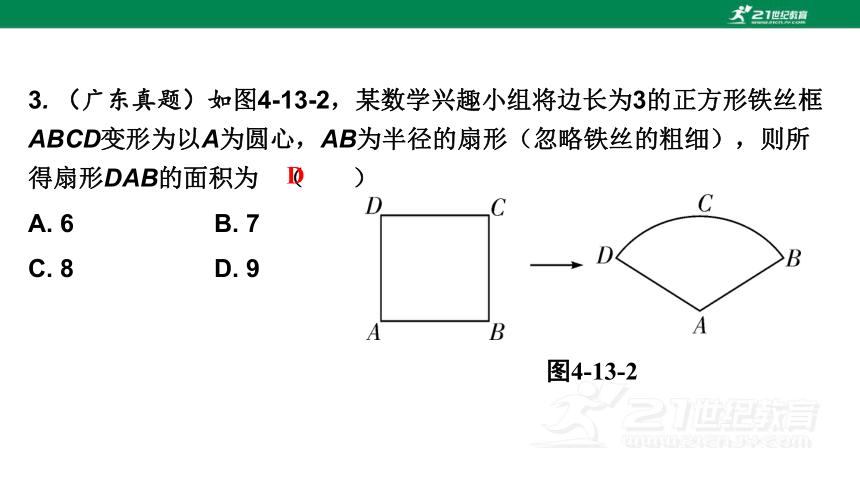
3. (广东真题)如图4-13-2,某数学兴趣小组将边长为3的正方形铁丝框ABCD变形为以A为圆心,AB为半径的扇形(忽略铁丝的粗细),则所得扇形DAB的面积为 ( )
A. 6 B. 7
C. 8 D. 9
图4-13-2
D
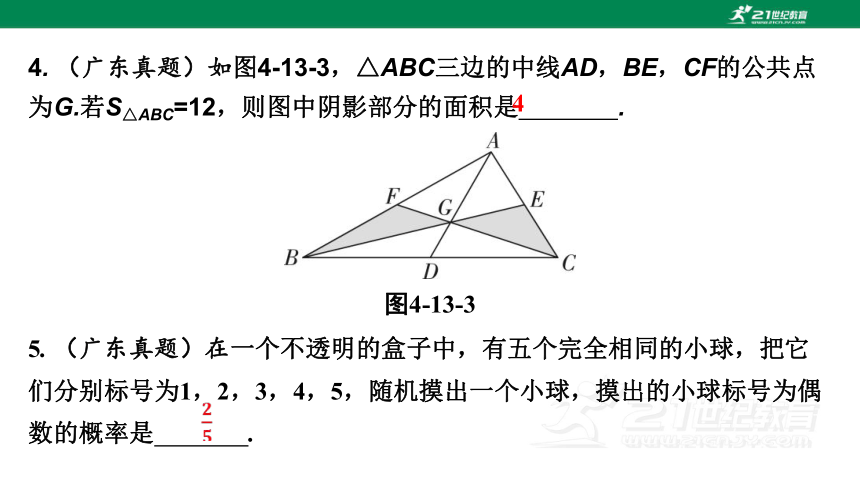
4. (广东真题)如图4-13-3,△ABC三边的中线AD,BE,CF的公共点为G.若S△ABC=12,则图中阴影部分的面积是 .
图4-13-3
4
5. (广东真题)在一个不透明的盒子中,有五个完全相同的小球,把它们分别标号为1,2,3,4,5,随机摸出一个小球,摸出的小球标号为偶数的概率是 .
(1)点、线、面、角
①通过实物和模型,了解从物体抽象出来的几何体、平面、直线和点等概念.
②会比较线段的长短,理解线段的和、差,以及线段中点的意义.
③掌握基本事实:两点确定一条直线.
④掌握基本事实:两点之间线段最短.
课标要求
⑤理解两点间距离的意义,能度量和表达两点间的距离.
⑥理解角的概念,能比较角的大小;认识度、分、秒等角的度量单位,能进行简单的单位换算,会计算角的和、差.
⑦了解角平分线的概念.
(2)相交线与平行线
①理解对顶角、余角、补角等概念,探索并掌握对顶角相等、同角(或等角)的余角相等、同角(或等角)的补角相等的性质.
②理解垂线、垂线段等概念,能用三角板或量角器过一点画已知直线的垂线.
③掌握基本事实:在同一平面内,过一点有且只有一条直线与已知直线垂直.
④理解点到直线的距离的意义,能度量点到直线的距离.
⑤识别同位角、内错角、同旁内角.
⑥理解平行线的概念.
⑦掌握平行线基本事实Ⅰ:过直线外一点有且只有一条直线与这条直线平行.
⑧掌握平行线基本事实Ⅱ:两条直线被第三条直线所截,如果同位角相等,那么这两条直线平行.
⑨探索并证明平行线的判定定理:两条直线被第三条直线所截,如果内错角相等(或同旁内角互补),那么这两条直线平行.
⑩掌握平行线的性质定理Ⅰ:两条平行直线被第三条直线所截,同位角相等. *了解定理的证明.
探索并证明平行线的性质定理Ⅱ:两条平行直线被第三条直线所截,内错角相等(或同旁内角互补).
能用三角板和直尺过已知直线外一点画这条直线的平行线.
了解平行于同一条直线的两条直线平行.
(3)定义、命题、定理
①通过具体实例,了解定义、命题、定理、推论的意义.
②结合具体实例,会区分命题的条件和结论,了解原命题及其逆命题的概念.会识别两个互逆的命题,知道原命题成立其逆命题不一定成立.
③知道证明的意义和证明的必要性,知道数学思维要合乎逻辑,知道可以用不同的形式表述证明的过程,会用综合法的证明格式.
④了解反例的作用,知道利用反例可以判断一个命题是错误的.
⑤通过实例体会反证法的含义.
对接教材 人教:七上第四章 几何图形初步;七下第五章 相交线与平行线
北师:七上第四章 基本平面图形;七下第二章 相交线与平行线;
八上第七章 平行线的证明
考点梳理
考点复习
1.直线、射线与线段
(1)直线 端点,射线有1个端点,线段有 个端点.
(2)经过 有且只有一条直线,简述为两点确定一条直线.
(3)两点之间的所有连线中, 最短,简述为两点之间线段最短.
(4)两点之间线段的 ,叫做这两点之间的距离
没有
2
两点
线段
长度
广东省对应考点例题
例1.(1)木匠师傅锯木料时,一般先在木板上画出两个点,然后过这两点弹出一条墨线,其依据的数学原理是 ;
(2)如图4-13-4,从公园甲到公园乙的三条路线中,最短的是 (填序号),这是因为 .
图4-13-4
两点确定一条直线
③
两点之间线段最短
2.角的相关概念
(1)由两条具有公共端点的 所组成的图形叫做角.两条射线的公共端点是这个角的顶点.
(2)按照角的大小,角可分为锐角、 、 、平角和周角.
(3)1周角=2平角=4直角=360°.
(4)1°=60',1'=60″.
射线
直角
钝角
(5)余角、补角:
如果两个角的和是90°,那么称这两个角互为余角,同角或等角的余角
;如果两个角的和是180°,那么称这两个角互为补角,同角或等角的补角
相等
相等
例2.(1)如图4-13-5,O是角的顶点,用三种不同的方法表示这个角为
, , ;
图4-13-5
∠AOB
∠1
∠O
(2)计算:13.17°= ° ' ″;
(3)若∠A=35°,则∠A的余角为 ,∠A的补角为 ;
(4)如图4-13-6,过直线AB上一点O作射线OC,∠BOC=29°18',则∠AOC的度数为 .
图4-13-6
13
10
12
55°
145°
150°42'
3.角的平分线
从一个角的顶点引出的一条射线,把这个角分成两个 的角,这条射线叫做这个角的平分线
例3. 如图4-13-7,已知O是直线AB上一点,∠1=50°,OF平分∠BOE,则∠2的度数为 .
图4-13-7
相等
65°
4.对顶角
对顶角 .互为对顶角的两个角相等,但相等的两个角不一定是对顶角
例4. 如图4-13-8是对顶角量角器,用它测量角的原理是 .
图4-13-8
相等
对顶角相等
5.垂直的性质
(1)在同一平面内,过一点 一条直线与已知直线垂直.
(2)直线外一点与直线上各点连接的所有线段中, 最短
例5.如图4-13-9,村庄A到公路BC的最短距离是AD的长,其根据的数学原理是 .
图4-13-9
有且只有
垂线段
垂线段最短
6.三线八角(如图4-13-10)
(1)同位角:∠1与∠5,∠2与∠6,∠4与 ,∠3与 .
(2)内错角:∠2与 ,∠3与∠5.
(3)同旁内角:∠3与∠8,∠2与
图4-13-10
∠8
∠7
∠8
∠5
例6.如图4-13-11,同位角有 对,内错角有 对,同旁内角有
对.
图4-13-11
6
4
4
7.平行线的判定与性质(如图4-13-12)
(1)同位角 两直线平行.
判定:∵∠1=∠2,∴l1∥l2.
性质:∵l1∥l2,∴∠1=∠2.
(2)内错角相等 两直线 .
判定:∵∠2=∠3,∴l1∥l2.
性质:∵l1∥l2,∴∠2=∠3.
(3)同旁内角 两直线平行.
判定:∵∠2+∠4=180°,∴l1∥l2.
性质:∵l1∥l2,∴∠2+∠4=180°
图4-13-12
相等
平行
互补
例7.如图4-13-13,填空:
(1)若∠A=∠3,则 ∥ ;
(2)若∠2=∠E,则 ∥ ;
(3)若∠A+∠ABE=180°,则 ∥ ;
(4)若BD∥CE,则∠DBC= ;
(5)若AD∥BE,则∠D= ;
(6)若BD∥CE,则∠DBC+∠4= .
图4-13-13
AD
BE
BD
CE
AD
BE
∠5
∠2
180°
例8.如图4-13-14,已知AB∥CD,求证:∠BED=∠B+∠D.(完成证明过程)
证明:过点E作EF∥AB.
∴∠1= .
∵AB∥CD(已知),
∴EF∥CD( ).
∴∠2= .
∴∠BED=∠1+∠2=∠B+∠D.
图4-13-14
∠B
平行于同一条直线的两条直线平行
∠D
8.平行公理
(1)过直线外一点, 一条直线与这条直线平行.
(2)平行于同一条直线的两条直线
有且只有
平行
9.定义、命题、定理
(1)对名称和术语的含义加以描述,作出明确的规定,即给出它们的
.
(2)判断一件事情的句子,叫做 .每个命题都由题设(或条件)和 两部分组成.正确的命题称为 ,不正确的命题称为
.要说明一个命题是假命题,常常可以举出一个例子,使它具备命题的条件,而不具有命题的结论,这种例子称为 .
定义
命题
结论
真命题
假命题
反例
(3)题设、结论正好相反的两个命题叫做互逆命题.如果把其中一个叫做原命题,那么另一个叫做它的 .
(4)公认的真命题称为公理.除公理外,其他命题的真假都需要通过演绎推理的方法进行判断.演绎推理的过程称为 ,经过证明的 命题称为定理.
(5)证明方法:综合法、分析法、反证法等
逆命题
证明
真
两个角相等
这两个角是同位角
-2
(答案不唯一)
如果两个角相等,那么这两个角是
对顶角
假
a≥0
广东中考
1. (2022·广东题4,3分,平行线的性质)如图4-13-15,直线a∥b,∠1=40°,则∠2= ( )
A. 30° B. 40°
C. 50° D. 60°
图4-13-15
B
2. (2023·广东题4,3分,平行线的性质)如图4-13-16,街道AB与CD平行,拐角∠ABC=137°,则拐角∠BCD= ( )
A. 43° B. 53°
C. 107° D. 137°
图4-13-16
D
3. (2024·广东题4,3分,平行线的判定与性质)如图4-13-17,一把直尺、两个含30°的三角尺拼接在一起,则∠ACE的度数为 ( )
A. 120° B. 90°
C. 60° D. 30°
图4-13-17
C
高分击破
【典型考点】平行线的判定与性质 得分点分析
1. (人教七下P20第2题改编)如图4-13-18,在△ABC中,D是AB上一点,E是AC上一点,∠BDE=140°,∠B=40°,∠AED=60°.
(1)判断DE与BC的位置关系,并说明理由;
解:(1)DE∥BC. ···············1分(判断出DE∥BC得1分)
理由:∵∠BDE=140°,∠B=40°,
∴∠B+∠BDE=180°. ···············2分(计算同旁内角的和得1分)
∴DE∥BC. ···············4分(利用“同旁内角互补,两直线平行”得2分)
(2)求∠C的度数.
(2)∵DE∥BC,
∴∠C=∠AED. ···············6分(利用“两直线
平行,同位角相等”得2分)
∵∠AED=60°,
∴∠C=60°. ··············· 7分(等量代换得1分)
温馨提示:此类考题可能见于广东省中考数学试卷的第17题,分值一般为7分,答题时要注意书写格式,分步书写,慢做会求全对,评卷老师是分步给分的哦!
【典型错例】在平行线的判定与性质的运用过程中,不能正确找出对应的同位角、内错角或同旁内角
2. 如图4-13-19,直线AB,CD分别和直线MN相交于点E,F,EG平分∠BEN,FH平分∠DFN. 若AB∥CD,则EG和FH是否平行?请说明理由.
图4-13-19
【生长式训练】知识生长→变式创新
3. (中考创新,原创题)如图4-13-20,已知直线GH分别与直线AB,CD交于点E,F,且EM∥FN.
知识种子:基本概念
(1)①若∠AEG=∠CFE,则直线AB与CD的位置关系是 ;
②若∠NFE=60°,则∠MEF的度数为 ;
图4-13-20
AB∥CD
60°
种子生长:平行线的判定与性质
(2)若EM平分∠BEF,FN平分∠CFE.
①求证:AB∥CD;
①证明:∵EM∥FN,∴∠MEF=∠NFE.
∵EM平分∠BEF,FN平分∠CFE,∴∠BEF=2∠MEF,∠CFE=2∠NFE.
∴∠BEF=∠CFE.∴AB∥CD.
图4-13-20
②若∠AEF=46°,求∠NFE的度数;
图4-13-20
生长变式:图形变式
(3)如图4-13-21,若EM平分∠AEF交CD于点M,且∠FEM=∠EMF.求证:AB∥CD;
证明:∵EM平分∠AEF,∴∠AEM=∠FEM.
又∵∠FEM=∠EMF,∴∠AEM=∠EMF.
∴AB∥CD.
图4-13-21
种子成树:综合创新
(4)在(3)的条件下,若G是射线MD上一动点(不与点M,F重合),EH平分∠FEG交CD于点H,过点H作HN⊥EM于点N,设∠EHN=α,∠EGF=β.试判断α与β的数量关系,并说明理由.
图4-13-21
图4-13-21
答图4-13-1
答图4-13-2
中考演练
(限时15分钟)
一、选择题
1. (2024·重庆)如图4-13-22,AB∥CD,∠1=65°,则∠2的度数是
( )
A. 105° B. 115°
C. 125° D. 135°
图4-13-22
B
2. (2024·兰州)如图4-13-23,小明在地图上量得∠1=∠2,由此判断幸福大街与平安大街互相平行,他判断的依据是 ( )
A. 同位角相等,两直线平行
B. 内错角相等,两直线平行
C. 同旁内角互补,两直线平行
D. 对顶角相等
图4-13-23
B
3. (2024·湖北)如图4-13-24,一条公路的两侧铺设了AB,CD两条平行管道,并有纵向管道AC连通.若∠1=120°,则∠2的度数是 ( )
A. 50° B. 60°
C. 70° D. 80°
B
4. (2024·赤峰)将一副三角尺(厚度不计)按如图4-13-25所示摆放,使有刻度的两条边互相平行,则图中∠1的度数为 ( )
A. 100° B. 105°
C. 115° D. 120°
B
5. (2024·深圳,跨学科融合)如图4-13-26,一束平行光线照射平面镜后反射,若入射光线与平面镜夹角∠1=50°,则反射光线与平面镜夹角∠4的度数为 ( )
A. 40° B. 50°
C. 60° D. 70°
B
二、填空题
6. (2024·广西)已知∠1与∠2为对顶角,∠1=35°,则∠2= °.
7. (2024·宿迁)命题“两直线平行,同位角相等”的逆命题是___________
.
35
同位角
相等,两直线平行
8. (2024·连云港)如图4-13-27,直线a∥b,直线l⊥a,∠1=120°,则∠2= °.
30
三、解答题
9. (2024·自贡)如图4-13-28,在△ABC中,DE∥BC,∠EDF=∠C.
(1)求证:∠BDF=∠A;
(1)证明:∵DE∥BC,∴∠C=∠AED.
∵∠EDF=∠C,∴∠AED=∠EDF.
∴DF∥AC.∴∠BDF=∠A.
(2)若∠A=45°,DF平分∠BDE,请直接写出△ABC的形状.
(2)解:△ABC是等腰直角三角形.
【提示】∵∠A=45°,∠BDF=∠A,∴∠BDF=45°.
∵DF平分∠BDE,∴∠BDE=2∠BDF=90°.
∵DE∥BC,∴∠BDE+∠B=180°.
∴∠B=180°-∠BDE=90°.∴△ABC是直角三角形.
又∵∠C=180°-∠A-∠B=45°,∴∠A=∠C.∴BA=BC.
∴△ABC是等腰直角三角形.
10. (2022·武汉)如图4-13-29,在四边形ABCD中,AD∥BC,∠B=80°.
(1)求∠BAD的度数;
(1)解:∵AD∥BC,∴∠B+∠BAD=180°.
∵∠B=80°,∴∠BAD=180°-∠B=100°.
(2)AE平分∠BAD交BC于点E,∠BCD=50°. 求证:AE∥DC.
命题趋势
( 限时 5 分钟)
(教材创新改编)如图4-13-30,已知直线DE∥AB.
(1)尺规作图:过点B作BM∥AD,交DE于点C;(不写作法,保留作图痕迹)
解:(1)如答图4-13-3,BM即为所作.
答图4-13-3
(2)在(1)的条件下,请写出图中以点C为顶点且与∠A相等的角,并说明理由.
(2)图中以点C为顶点且与∠A相等的角
有∠MCE,∠DCB.
理由:∵DE∥AB,∴∠DCB=∠MBN.
由(1)作图可知∠A=∠MBN,∴∠DCB=∠A.
∵∠MCE=∠DCB,∴∠MCE=∠DCB=∠A.
答图4-13-3
命题解读:根据最新课程标准和近三年中考命题动向,预测2025年中考命题方向可能注重考查线、角、相交线与平行线的基本概念,如对顶角、同位角、内错角、同旁内角等;强调平行线的判定与性质,可能会结合三角形、四边形、平面直角坐标系等知识考查,也可能会结合现实背景或跨学科背景进行考查;还可能会考查创新题型,如考查与直尺或三角尺结合、与尺规作图结合等.
第四章 三 角 形
第13课时 线、角、相交线与平行线
课前循环练
(限时5分钟)
1. (广东真题)下列式子是完全平方式的是 ( )
A. a2+ab+b2 B. a2+2a+2
C. a2-2b+b2 D. a2+2a+1
D
2. (广东真题)如图4-13-1,AB∥CD,∠DEC=100°,∠C=40°,则∠B的大小是 ( )
A. 30° B. 40°
C. 50° D. 60°
图4-13-1
B
3. (广东真题)如图4-13-2,某数学兴趣小组将边长为3的正方形铁丝框ABCD变形为以A为圆心,AB为半径的扇形(忽略铁丝的粗细),则所得扇形DAB的面积为 ( )
A. 6 B. 7
C. 8 D. 9
图4-13-2
D
4. (广东真题)如图4-13-3,△ABC三边的中线AD,BE,CF的公共点为G.若S△ABC=12,则图中阴影部分的面积是 .
图4-13-3
4
5. (广东真题)在一个不透明的盒子中,有五个完全相同的小球,把它们分别标号为1,2,3,4,5,随机摸出一个小球,摸出的小球标号为偶数的概率是 .
(1)点、线、面、角
①通过实物和模型,了解从物体抽象出来的几何体、平面、直线和点等概念.
②会比较线段的长短,理解线段的和、差,以及线段中点的意义.
③掌握基本事实:两点确定一条直线.
④掌握基本事实:两点之间线段最短.
课标要求
⑤理解两点间距离的意义,能度量和表达两点间的距离.
⑥理解角的概念,能比较角的大小;认识度、分、秒等角的度量单位,能进行简单的单位换算,会计算角的和、差.
⑦了解角平分线的概念.
(2)相交线与平行线
①理解对顶角、余角、补角等概念,探索并掌握对顶角相等、同角(或等角)的余角相等、同角(或等角)的补角相等的性质.
②理解垂线、垂线段等概念,能用三角板或量角器过一点画已知直线的垂线.
③掌握基本事实:在同一平面内,过一点有且只有一条直线与已知直线垂直.
④理解点到直线的距离的意义,能度量点到直线的距离.
⑤识别同位角、内错角、同旁内角.
⑥理解平行线的概念.
⑦掌握平行线基本事实Ⅰ:过直线外一点有且只有一条直线与这条直线平行.
⑧掌握平行线基本事实Ⅱ:两条直线被第三条直线所截,如果同位角相等,那么这两条直线平行.
⑨探索并证明平行线的判定定理:两条直线被第三条直线所截,如果内错角相等(或同旁内角互补),那么这两条直线平行.
⑩掌握平行线的性质定理Ⅰ:两条平行直线被第三条直线所截,同位角相等. *了解定理的证明.
探索并证明平行线的性质定理Ⅱ:两条平行直线被第三条直线所截,内错角相等(或同旁内角互补).
能用三角板和直尺过已知直线外一点画这条直线的平行线.
了解平行于同一条直线的两条直线平行.
(3)定义、命题、定理
①通过具体实例,了解定义、命题、定理、推论的意义.
②结合具体实例,会区分命题的条件和结论,了解原命题及其逆命题的概念.会识别两个互逆的命题,知道原命题成立其逆命题不一定成立.
③知道证明的意义和证明的必要性,知道数学思维要合乎逻辑,知道可以用不同的形式表述证明的过程,会用综合法的证明格式.
④了解反例的作用,知道利用反例可以判断一个命题是错误的.
⑤通过实例体会反证法的含义.
对接教材 人教:七上第四章 几何图形初步;七下第五章 相交线与平行线
北师:七上第四章 基本平面图形;七下第二章 相交线与平行线;
八上第七章 平行线的证明
考点梳理
考点复习
1.直线、射线与线段
(1)直线 端点,射线有1个端点,线段有 个端点.
(2)经过 有且只有一条直线,简述为两点确定一条直线.
(3)两点之间的所有连线中, 最短,简述为两点之间线段最短.
(4)两点之间线段的 ,叫做这两点之间的距离
没有
2
两点
线段
长度
广东省对应考点例题
例1.(1)木匠师傅锯木料时,一般先在木板上画出两个点,然后过这两点弹出一条墨线,其依据的数学原理是 ;
(2)如图4-13-4,从公园甲到公园乙的三条路线中,最短的是 (填序号),这是因为 .
图4-13-4
两点确定一条直线
③
两点之间线段最短
2.角的相关概念
(1)由两条具有公共端点的 所组成的图形叫做角.两条射线的公共端点是这个角的顶点.
(2)按照角的大小,角可分为锐角、 、 、平角和周角.
(3)1周角=2平角=4直角=360°.
(4)1°=60',1'=60″.
射线
直角
钝角
(5)余角、补角:
如果两个角的和是90°,那么称这两个角互为余角,同角或等角的余角
;如果两个角的和是180°,那么称这两个角互为补角,同角或等角的补角
相等
相等
例2.(1)如图4-13-5,O是角的顶点,用三种不同的方法表示这个角为
, , ;
图4-13-5
∠AOB
∠1
∠O
(2)计算:13.17°= ° ' ″;
(3)若∠A=35°,则∠A的余角为 ,∠A的补角为 ;
(4)如图4-13-6,过直线AB上一点O作射线OC,∠BOC=29°18',则∠AOC的度数为 .
图4-13-6
13
10
12
55°
145°
150°42'
3.角的平分线
从一个角的顶点引出的一条射线,把这个角分成两个 的角,这条射线叫做这个角的平分线
例3. 如图4-13-7,已知O是直线AB上一点,∠1=50°,OF平分∠BOE,则∠2的度数为 .
图4-13-7
相等
65°
4.对顶角
对顶角 .互为对顶角的两个角相等,但相等的两个角不一定是对顶角
例4. 如图4-13-8是对顶角量角器,用它测量角的原理是 .
图4-13-8
相等
对顶角相等
5.垂直的性质
(1)在同一平面内,过一点 一条直线与已知直线垂直.
(2)直线外一点与直线上各点连接的所有线段中, 最短
例5.如图4-13-9,村庄A到公路BC的最短距离是AD的长,其根据的数学原理是 .
图4-13-9
有且只有
垂线段
垂线段最短
6.三线八角(如图4-13-10)
(1)同位角:∠1与∠5,∠2与∠6,∠4与 ,∠3与 .
(2)内错角:∠2与 ,∠3与∠5.
(3)同旁内角:∠3与∠8,∠2与
图4-13-10
∠8
∠7
∠8
∠5
例6.如图4-13-11,同位角有 对,内错角有 对,同旁内角有
对.
图4-13-11
6
4
4
7.平行线的判定与性质(如图4-13-12)
(1)同位角 两直线平行.
判定:∵∠1=∠2,∴l1∥l2.
性质:∵l1∥l2,∴∠1=∠2.
(2)内错角相等 两直线 .
判定:∵∠2=∠3,∴l1∥l2.
性质:∵l1∥l2,∴∠2=∠3.
(3)同旁内角 两直线平行.
判定:∵∠2+∠4=180°,∴l1∥l2.
性质:∵l1∥l2,∴∠2+∠4=180°
图4-13-12
相等
平行
互补
例7.如图4-13-13,填空:
(1)若∠A=∠3,则 ∥ ;
(2)若∠2=∠E,则 ∥ ;
(3)若∠A+∠ABE=180°,则 ∥ ;
(4)若BD∥CE,则∠DBC= ;
(5)若AD∥BE,则∠D= ;
(6)若BD∥CE,则∠DBC+∠4= .
图4-13-13
AD
BE
BD
CE
AD
BE
∠5
∠2
180°
例8.如图4-13-14,已知AB∥CD,求证:∠BED=∠B+∠D.(完成证明过程)
证明:过点E作EF∥AB.
∴∠1= .
∵AB∥CD(已知),
∴EF∥CD( ).
∴∠2= .
∴∠BED=∠1+∠2=∠B+∠D.
图4-13-14
∠B
平行于同一条直线的两条直线平行
∠D
8.平行公理
(1)过直线外一点, 一条直线与这条直线平行.
(2)平行于同一条直线的两条直线
有且只有
平行
9.定义、命题、定理
(1)对名称和术语的含义加以描述,作出明确的规定,即给出它们的
.
(2)判断一件事情的句子,叫做 .每个命题都由题设(或条件)和 两部分组成.正确的命题称为 ,不正确的命题称为
.要说明一个命题是假命题,常常可以举出一个例子,使它具备命题的条件,而不具有命题的结论,这种例子称为 .
定义
命题
结论
真命题
假命题
反例
(3)题设、结论正好相反的两个命题叫做互逆命题.如果把其中一个叫做原命题,那么另一个叫做它的 .
(4)公认的真命题称为公理.除公理外,其他命题的真假都需要通过演绎推理的方法进行判断.演绎推理的过程称为 ,经过证明的 命题称为定理.
(5)证明方法:综合法、分析法、反证法等
逆命题
证明
真
两个角相等
这两个角是同位角
-2
(答案不唯一)
如果两个角相等,那么这两个角是
对顶角
假
a≥0
广东中考
1. (2022·广东题4,3分,平行线的性质)如图4-13-15,直线a∥b,∠1=40°,则∠2= ( )
A. 30° B. 40°
C. 50° D. 60°
图4-13-15
B
2. (2023·广东题4,3分,平行线的性质)如图4-13-16,街道AB与CD平行,拐角∠ABC=137°,则拐角∠BCD= ( )
A. 43° B. 53°
C. 107° D. 137°
图4-13-16
D
3. (2024·广东题4,3分,平行线的判定与性质)如图4-13-17,一把直尺、两个含30°的三角尺拼接在一起,则∠ACE的度数为 ( )
A. 120° B. 90°
C. 60° D. 30°
图4-13-17
C
高分击破
【典型考点】平行线的判定与性质 得分点分析
1. (人教七下P20第2题改编)如图4-13-18,在△ABC中,D是AB上一点,E是AC上一点,∠BDE=140°,∠B=40°,∠AED=60°.
(1)判断DE与BC的位置关系,并说明理由;
解:(1)DE∥BC. ···············1分(判断出DE∥BC得1分)
理由:∵∠BDE=140°,∠B=40°,
∴∠B+∠BDE=180°. ···············2分(计算同旁内角的和得1分)
∴DE∥BC. ···············4分(利用“同旁内角互补,两直线平行”得2分)
(2)求∠C的度数.
(2)∵DE∥BC,
∴∠C=∠AED. ···············6分(利用“两直线
平行,同位角相等”得2分)
∵∠AED=60°,
∴∠C=60°. ··············· 7分(等量代换得1分)
温馨提示:此类考题可能见于广东省中考数学试卷的第17题,分值一般为7分,答题时要注意书写格式,分步书写,慢做会求全对,评卷老师是分步给分的哦!
【典型错例】在平行线的判定与性质的运用过程中,不能正确找出对应的同位角、内错角或同旁内角
2. 如图4-13-19,直线AB,CD分别和直线MN相交于点E,F,EG平分∠BEN,FH平分∠DFN. 若AB∥CD,则EG和FH是否平行?请说明理由.
图4-13-19
【生长式训练】知识生长→变式创新
3. (中考创新,原创题)如图4-13-20,已知直线GH分别与直线AB,CD交于点E,F,且EM∥FN.
知识种子:基本概念
(1)①若∠AEG=∠CFE,则直线AB与CD的位置关系是 ;
②若∠NFE=60°,则∠MEF的度数为 ;
图4-13-20
AB∥CD
60°
种子生长:平行线的判定与性质
(2)若EM平分∠BEF,FN平分∠CFE.
①求证:AB∥CD;
①证明:∵EM∥FN,∴∠MEF=∠NFE.
∵EM平分∠BEF,FN平分∠CFE,∴∠BEF=2∠MEF,∠CFE=2∠NFE.
∴∠BEF=∠CFE.∴AB∥CD.
图4-13-20
②若∠AEF=46°,求∠NFE的度数;
图4-13-20
生长变式:图形变式
(3)如图4-13-21,若EM平分∠AEF交CD于点M,且∠FEM=∠EMF.求证:AB∥CD;
证明:∵EM平分∠AEF,∴∠AEM=∠FEM.
又∵∠FEM=∠EMF,∴∠AEM=∠EMF.
∴AB∥CD.
图4-13-21
种子成树:综合创新
(4)在(3)的条件下,若G是射线MD上一动点(不与点M,F重合),EH平分∠FEG交CD于点H,过点H作HN⊥EM于点N,设∠EHN=α,∠EGF=β.试判断α与β的数量关系,并说明理由.
图4-13-21
图4-13-21
答图4-13-1
答图4-13-2
中考演练
(限时15分钟)
一、选择题
1. (2024·重庆)如图4-13-22,AB∥CD,∠1=65°,则∠2的度数是
( )
A. 105° B. 115°
C. 125° D. 135°
图4-13-22
B
2. (2024·兰州)如图4-13-23,小明在地图上量得∠1=∠2,由此判断幸福大街与平安大街互相平行,他判断的依据是 ( )
A. 同位角相等,两直线平行
B. 内错角相等,两直线平行
C. 同旁内角互补,两直线平行
D. 对顶角相等
图4-13-23
B
3. (2024·湖北)如图4-13-24,一条公路的两侧铺设了AB,CD两条平行管道,并有纵向管道AC连通.若∠1=120°,则∠2的度数是 ( )
A. 50° B. 60°
C. 70° D. 80°
B
4. (2024·赤峰)将一副三角尺(厚度不计)按如图4-13-25所示摆放,使有刻度的两条边互相平行,则图中∠1的度数为 ( )
A. 100° B. 105°
C. 115° D. 120°
B
5. (2024·深圳,跨学科融合)如图4-13-26,一束平行光线照射平面镜后反射,若入射光线与平面镜夹角∠1=50°,则反射光线与平面镜夹角∠4的度数为 ( )
A. 40° B. 50°
C. 60° D. 70°
B
二、填空题
6. (2024·广西)已知∠1与∠2为对顶角,∠1=35°,则∠2= °.
7. (2024·宿迁)命题“两直线平行,同位角相等”的逆命题是___________
.
35
同位角
相等,两直线平行
8. (2024·连云港)如图4-13-27,直线a∥b,直线l⊥a,∠1=120°,则∠2= °.
30
三、解答题
9. (2024·自贡)如图4-13-28,在△ABC中,DE∥BC,∠EDF=∠C.
(1)求证:∠BDF=∠A;
(1)证明:∵DE∥BC,∴∠C=∠AED.
∵∠EDF=∠C,∴∠AED=∠EDF.
∴DF∥AC.∴∠BDF=∠A.
(2)若∠A=45°,DF平分∠BDE,请直接写出△ABC的形状.
(2)解:△ABC是等腰直角三角形.
【提示】∵∠A=45°,∠BDF=∠A,∴∠BDF=45°.
∵DF平分∠BDE,∴∠BDE=2∠BDF=90°.
∵DE∥BC,∴∠BDE+∠B=180°.
∴∠B=180°-∠BDE=90°.∴△ABC是直角三角形.
又∵∠C=180°-∠A-∠B=45°,∴∠A=∠C.∴BA=BC.
∴△ABC是等腰直角三角形.
10. (2022·武汉)如图4-13-29,在四边形ABCD中,AD∥BC,∠B=80°.
(1)求∠BAD的度数;
(1)解:∵AD∥BC,∴∠B+∠BAD=180°.
∵∠B=80°,∴∠BAD=180°-∠B=100°.
(2)AE平分∠BAD交BC于点E,∠BCD=50°. 求证:AE∥DC.
命题趋势
( 限时 5 分钟)
(教材创新改编)如图4-13-30,已知直线DE∥AB.
(1)尺规作图:过点B作BM∥AD,交DE于点C;(不写作法,保留作图痕迹)
解:(1)如答图4-13-3,BM即为所作.
答图4-13-3
(2)在(1)的条件下,请写出图中以点C为顶点且与∠A相等的角,并说明理由.
(2)图中以点C为顶点且与∠A相等的角
有∠MCE,∠DCB.
理由:∵DE∥AB,∴∠DCB=∠MBN.
由(1)作图可知∠A=∠MBN,∴∠DCB=∠A.
∵∠MCE=∠DCB,∴∠MCE=∠DCB=∠A.
答图4-13-3
命题解读:根据最新课程标准和近三年中考命题动向,预测2025年中考命题方向可能注重考查线、角、相交线与平行线的基本概念,如对顶角、同位角、内错角、同旁内角等;强调平行线的判定与性质,可能会结合三角形、四边形、平面直角坐标系等知识考查,也可能会结合现实背景或跨学科背景进行考查;还可能会考查创新题型,如考查与直尺或三角尺结合、与尺规作图结合等.
同课章节目录
