中考数学复习知识梳理第五章四边形第20课时菱形、矩形、正方形、梯形课件(共53张PPT)
文档属性
| 名称 | 中考数学复习知识梳理第五章四边形第20课时菱形、矩形、正方形、梯形课件(共53张PPT) |  | |
| 格式 | ppt | ||
| 文件大小 | 6.4MB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 通用版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2025-05-31 09:33:34 | ||
图片预览








文档简介
(共53张PPT)
第五章 四 边 形
第20课时 菱形、矩形、正方形、梯形
课前循环练
(限时5分钟)
1. (广东真题)在下列交通标志中,既是轴对称图形,又是中心对称图形的是 ( )
C
B
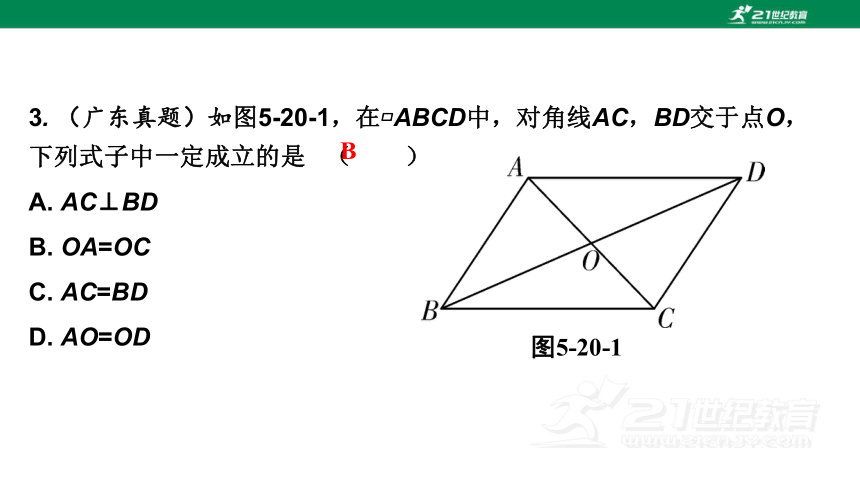
3. (广东真题)如图5-20-1,在 ABCD中,对角线AC,BD交于点O,下列式子中一定成立的是 ( )
A. AC⊥BD
B. OA=OC
C. AC=BD
D. AO=OD
图5-20-1
B
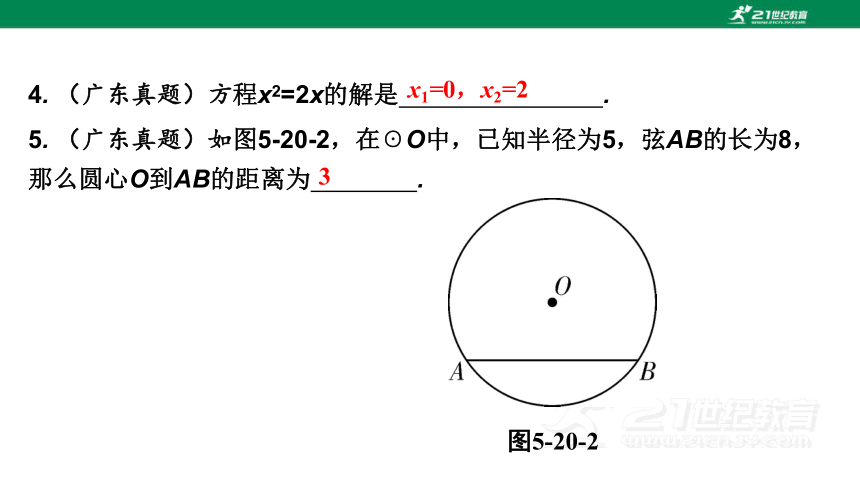
4. (广东真题)方程x2=2x的解是 .
5. (广东真题)如图5-20-2,在☉O中,已知半径为5,弦AB的长为8,那么圆心O到AB的距离为 .
图5-20-2
x1=0,x2=2
3
①理解平行四边形、矩形、菱形、正方形、梯形的概念,以及它们之间的关系.
②探索并证明矩形、菱形的性质定理:矩形的四个角都是直角,对角线相等;菱形的四条边相等,对角线互相垂直.探索并证明矩形、菱形的判定定理:三个角是直角的四边形是矩形,对角线相等的平行四边形是矩形;四边相等的四边形是菱形,对角线互相垂直的平行四边形是菱形. 正方形既是矩形,又是菱形;理解矩形、菱形、正方形之间的包含关系.
课标要求
对接教材 人教:八下第十八章 平行四边形(18.2 特殊的平行四边形)
北师:九上第一章 特殊平行四边形
考点梳理
广东省对应考点例题
例1. 在四边形ABCD中,AB∥DC,AD∥BC,如果添加一个条件,即可推出该四边形是矩形,那么这个条件可以是 ( )
A.∠D=90° B. AB=CD
C. AD=BC D. BC=CD
A
考点复习
1.矩形的概念
有一个角是 的平行四边形叫做矩形
直角
2.矩形的性质
(1)具有平行四边形的所有性质.
(2)矩形的四个角都是 .
(3)矩形的对角线 .
(4)矩形既是中心对称图形,也是轴对称图形,有 条对称轴
直角
相等
2
图5-20-3
B
3.矩形的判定
(1)有一个角是直角的平行四边形是矩形.
(2)对角线 的平行四边形是矩形.
(3)有三个角是 的四边形是矩形
相等
直角
例3. 如图5-20-4,在 ABCD中,对角线AC和BD相交于点O,则下面条件能判定四边形ABCD是矩形的是 ( )
A. AC=BD
B. AC⊥BD
C. OA=OC
D. AB=AD
图5-20-4
A
4.菱形的概念
有一组邻边 的平行四边形叫做菱形
例4. 下面四个定义中不正确的是 ( )
A.有一个角是直角的平行四边形叫做矩形
B.有一组邻边相等的四边形叫做菱形
C.有一组邻边相等,并且有一个角是直角的平行四边形叫做正方形
D.有一组邻边相等的平行四边形叫做菱形
相等
B
5.菱形的性质
(1)具有平行四边形的所有性质.
(2)菱形的四条边都 .
(3)菱形的对角线互相 ,每条对角线平分一组对角.
(4)菱形既是中心对称图形,也是轴对称图形,有 条对称轴
相等
垂直
2
例5. 在菱形ABCD中,AC,BD为对角线,下列说法一定正确的是( )
A. AC=BD
B. AC⊥BD
C.∠ABD=∠BAC
D.∠BAC+∠CAD=90°
B
6.菱形的判定
(1)有一组邻边相等的平行四边形是菱形.
(2)四条边 的四边形是菱形.
(3)对角线互相 的平行四边形是菱形
相等
垂直
例6. 如图5-20-5,下列选项中,能证明 ABCD是菱形的条件有 ( )
① AC⊥BD;② BA⊥AD;③ AB=BC;④ AC=BD.
A. ①②③ B. ②③
C. ③④ D. ①③
图5-20-5
D
7.正方形的概念
有一组邻边 ,并且有一个角是 的平行四边形叫做正方形
例7. 在四边形ABCD中,AB∥CD,∠B=∠D,∠A=90°,如果添加一个条件,即可推出该四边形是正方形,那么这个条件可以是 ( )
A. ∠D=90° B. AB=CD
C. BC=CD D. AC=BD
相等
直角
C
8.正方形的性质
正方形具有矩形和菱形的性质:
(1)边:四条边都 ,对边平行.
(2)角:四个角都是 .
(3)对角线:对角线相等且 ,每条对角线 一组对角.
(4)正方形既是中心对称图形,也是轴对称图形,有 条对称轴
相等
直角
互相垂直平分
平分
4
例8. 如图5-20-6,四边形ABCD是正方形,对角线AC,BD交于点O.下列结论:① OA=OB;② ∠ACB=45°;③ AC⊥BD;④正方形ABCD有4条对称轴.上述结论正确的有 ( )
A. ①②③④ B. ①②③
C. ②③④ D. ①③④
图5-20-6
A
9.正方形的判定
(1)有一组邻边 的矩形是正方形.
(2)对角线互相 的矩形是正方形.
(3)有一个角是 的菱形是正方形.
(4)对角线 的菱形是正方形
相等
垂直
直角
相等
例9. (1)在矩形ABCD中,对角线AC,BD交于点O,要使该矩形成为正方形,可添加的一个条件是 ;
(2)在菱形ABCD中,对角线AC,BD交于点O,要使该菱形成为正方形,可添加的一个条件是 .
AB=AD(答案不唯一)
AC=BD(答案不唯一)
10.平行四边形、矩形、菱形与正方形的关系
(1)从边、角分析:
(2)从对角线分析:
例10. 如图5-20-7,已知 ABCD的对角线AC与BD相交于点O,请你添加两个适当的条件: ,使 ABCD变为正方形.
图5-20-7
AB=BC,∠ABC=90°(答案不唯一)
11.梯形的概念
只有一组对边 的四边形叫做梯形.其中有一个角是直角的梯形叫做 梯形,两腰相等的梯形叫做 梯形
平行
直角
等腰
例11.如图5-20-8,在梯形ABCD中,AD∥BC,AD=3,AB=CD=4,∠A=120°,则下底BC的长为 .
图5-20-8
7
广东中考
1. (2022·广东题13,3分,菱形的性质)菱形的边长为5,则它的周长是
.
2. (2024·广东题15,3分,菱形的性质;三角形的面积)如图5-20-9,菱形ABCD的面积为24,E是AB的中点,F是BC上的动点. 若△BEF的面积为4,则图中阴影部分的面积为 .
图5-20-9
20
10
高分击破
【典型考点】矩形的判定与性质 得分点分析
1. (2024·兰州)如图5-20-10,在△ABC中,AB=AC,D是BC的中点,CE∥AD,AE⊥AD,EF⊥AC.
图5-20-10
(1)求证:四边形ADCE是矩形;
(1)证明:∵AB=AC,D是BC的中点,
∴AD⊥BC,即∠ADC=∠ADB=90°.
············1分(利用三线合一的性质得1分)
∵CE∥AD,∴∠ECD=∠ADB=90°. ··················2分(利用平行线的性质得1分)
∵AE⊥AD,∴∠EAD=90°. ··································3分(利用垂直的定义得1分)
∴∠ADC=∠ECD=∠EAD=90°.∴四边形ADCE是矩形. ··················4分(利用矩形的判定得1分)
图5-20-10
(2)若BC=4,CE=3,求EF的长.
图5-20-10
温馨提示:此类考题可能见于广东省中考数学试卷的第19题,分值一般为9分,答题时要注意书写格式,分步书写,慢做会求全对,评卷老师是分步给分的哦!
【典型错例】重复证明的错误
2. 如图5-20-11, ABCD的对角线AC的垂直平分线与边AD,BC分别相交于点E,F. 求证:四边形AFCE是菱形.
图5-20-11
错解分析
错解:∵四边形ABCD是平行四边形,
∴AD∥BC.∴∠EAO=∠FCO.
∵EF垂直平分AC,
∴AE=CE,AF=CF,AO=CO,EF⊥AC.
又∵∠AOE=∠COF,∴△AOE≌△COF(ASA).
∴AE=CF,OE=OF.∴AE=CE=CF=AF,AC与EF互相垂直平分.
∴四边形AFCE是菱形.
剖析:该解题过程犯了重复证明的错误,在证明四边相等后,又证明了对角线互相垂直平分,这两组条件都可以判定菱形,选其中一个即可.
图5-20-11
【生长式训练】知识生长→变式创新
3. (中考创新,原创题)如图5-20-12①,将矩形纸片ABCD沿对角线AC剪开,得到△ABC和△ACD,并且测得AB=3 cm,BC=4 cm.
图5-20-12
知识种子:基本概念
(1)将这两张三角形纸片按图5-20-12②的方式摆放,连接BD,则AC与BD的位置关系是 ;
图5-20-12
AC⊥BD
种子生长:矩形的判定与性质
(2)如图5-20-12③,将图5-20-12②中的△A'C'D纸片沿射线CA方向平移,连接BC',BA',直至BC'∥A'D.
①判断四边形A'BC'D的形状,并说明理由;
解:①四边形A'BC'D是矩形.
理由:如图5-20-12①,
在矩形ABCD中,∠D=90°,AD=BC,AD∥BC,
∴∠ACB=∠CAD.
∴在图5-20-12③中,BC=A'D,∠ACB=∠C'A'D,∠D=90°.
∵BC'∥A'D,∴∠C'A'D=∠A'C'B.
∴∠A'C'B=∠ACB.∴BC'=BC.
∴BC'=A'D.∴四边形A'BC'D是平行四边形.
又∵∠D=90°,∴四边形A'BC'D是矩形.
图5-20-12
答图5-20-1
②求平移的距离AC';
生长变式:图形变式
(3)如图5-20-13,将图5-20-12①中的△ACD以点A为旋转中心,按逆时针方向旋转∠α,使∠α=∠BAC,得到△AC'D,过点C作AC'的平行线,与DC'的延长线交于点E,判定四边形ACEC'的形状,并说明理由;
解:四边形ACEC'是菱形.
理由:如图5-20-12①,在矩形ABCD中,AB∥CD ∴∠ACD=∠BAC.
如图5-20-13,由旋转的性质,得AC'=AC,∠AC'D=∠BAC.
∵∠CAC'=∠α,∠α=∠BAC,
∴∠CAC'=∠AC'D.∴AC∥C'E.
又∵CE∥AC',∴四边形ACEC'是平行四边形.
又∵AC'=AC,∴四边形ACEC'是菱形.
图5-20-13
种子成树:综合创新
(4)如图5-20-14①,将图5-20-13中的△AC'D继续按逆时针方向旋转,使B,A,D三点在同一条直线上,连接CC',取CC'的中点F,连接AF并延长至点G,使FG=AF,连接CG,C'G.
图5-20-14
①判断四边形ACGC'的形状,并说明理由;
解:①四边形ACGC'是正方形.
理由:∵F为CC'的中点,∴C'F=CF.
又∵FG=AF,∴四边形ACGC'是平行四边形.
又∵AC=AC',∴四边形ACGC'是菱形.
∵∠AC'D=∠BAC,∠AC'D+∠DAC'=90°,
∴∠BAC+∠DAC'=90°.
∴∠CAC'=180°-(∠BAC+∠DAC')=90°.
∴四边形ACGC'是正方形.
图5-20-14
②如图5-20-14②,将图5-20-14①中△ABC沿着BD方向平移,使点B与点A重合,此时点A平移至点A',A'C与BC'交于点P,连接CC',求tan∠C'CP的值.
图5-20-14
中考演练
(限时15分钟)
一、选择题
1. (2024·成都)如图5-20-15,在矩形ABCD中,对角线AC与BD相交于点O,则下列结论一定正确的是 ( )
A. AB=AD
B. AC⊥BD
C. AC=BD
D. ∠ACB=∠ACD
图5-20-15
C
图5-20-16
C
3. (2024·通辽)如图5-20-17, ABCD的对角线AC,BD交于点O,以下条件不能证明 ABCD是菱形的是 ( )
A. ∠BAC=∠BCA
B. ∠ABD=∠CBD
C. OA2+OB2=AD2
D. AD2+OA2=OD2
图5-20-17
D
图5-20-18
B
图5-20-19
B
二、填空题
6. (2024·甘孜州)如图5-20-20,在菱形ABCD中,AB=2,则菱形ABCD的周长为 .
图5-20-20
8
7. (2024·兰州)如图5-20-21,四边形ABCD为正方形,△ADE为等边三角形,EF⊥AB于点F.若AD=4,则EF= .
图5-20-21
2
8. (2023·陕西)如图5-20-22,在矩形ABCD中,AB=3,BC=4.点E在边AD上,且ED=3,M,N分别是边AB,BC上的动点,且BM=BN,P是线段CE上的动点,连接PM,PN.若PM+PN=4,则线段PC的长为 .
图5-20-22
三、解答题
9. (2024·广安)如图5-20-23,菱形ABCD中,E,F分别是边AB,BC上的点,BE=BF,求证:∠DEF=∠DFE.
图5-20-23
10. (2024·长沙)如图5-20-24,在 ABCD中,对角线AC,BD相交于点O,∠ABC=90°.
(1)求证:AC=BD;
图5-20-24
(1)证明:∵四边形ABCD是平行四边形,∠ABC=90°,
∴四边形ABCD是矩形.∴AC=BD.
(2)点E在BC边上,满足∠CEO=∠COE. 若AB=6,BC=8,求CE的长及tan∠CEO的值.
答图5-20-2
命题趋势
( 限时 5 分钟)
图5-20-25
【知识技能】 (1)如图5-20-25①,当OE⊥AC时,G,Q,C三点重合,此时OQ与OP的数量关系为 ;
图5-20-25
【数学理解】(2)当正方形OEFG旋转到如图5-20-25②所示的位置时,猜想OQ与OP的数量关系,并说明理由;
答图5-20-3
答图5-20-3
【拓展探索】(3)在正方形的旋转过程中,
当DE=EF时,请直接写出DF的长.
答图5-20-4
答图5-20-5
命题解读:根据最新课程标准和近三年中考命题动向,预测2025年中考命题方向可能注重考查特殊四边形的基本概念、性质和判定方法,如通过具体图形判断它们的类型、计算相关角度或边长等;强调与其他几何图形的综合运用,可能与三角形、平行四边形、圆等结合;还可能会考查综合探究类题型,通过变换图形位置或构造特殊图形综合考查.
第五章 四 边 形
第20课时 菱形、矩形、正方形、梯形
课前循环练
(限时5分钟)
1. (广东真题)在下列交通标志中,既是轴对称图形,又是中心对称图形的是 ( )
C
B
3. (广东真题)如图5-20-1,在 ABCD中,对角线AC,BD交于点O,下列式子中一定成立的是 ( )
A. AC⊥BD
B. OA=OC
C. AC=BD
D. AO=OD
图5-20-1
B
4. (广东真题)方程x2=2x的解是 .
5. (广东真题)如图5-20-2,在☉O中,已知半径为5,弦AB的长为8,那么圆心O到AB的距离为 .
图5-20-2
x1=0,x2=2
3
①理解平行四边形、矩形、菱形、正方形、梯形的概念,以及它们之间的关系.
②探索并证明矩形、菱形的性质定理:矩形的四个角都是直角,对角线相等;菱形的四条边相等,对角线互相垂直.探索并证明矩形、菱形的判定定理:三个角是直角的四边形是矩形,对角线相等的平行四边形是矩形;四边相等的四边形是菱形,对角线互相垂直的平行四边形是菱形. 正方形既是矩形,又是菱形;理解矩形、菱形、正方形之间的包含关系.
课标要求
对接教材 人教:八下第十八章 平行四边形(18.2 特殊的平行四边形)
北师:九上第一章 特殊平行四边形
考点梳理
广东省对应考点例题
例1. 在四边形ABCD中,AB∥DC,AD∥BC,如果添加一个条件,即可推出该四边形是矩形,那么这个条件可以是 ( )
A.∠D=90° B. AB=CD
C. AD=BC D. BC=CD
A
考点复习
1.矩形的概念
有一个角是 的平行四边形叫做矩形
直角
2.矩形的性质
(1)具有平行四边形的所有性质.
(2)矩形的四个角都是 .
(3)矩形的对角线 .
(4)矩形既是中心对称图形,也是轴对称图形,有 条对称轴
直角
相等
2
图5-20-3
B
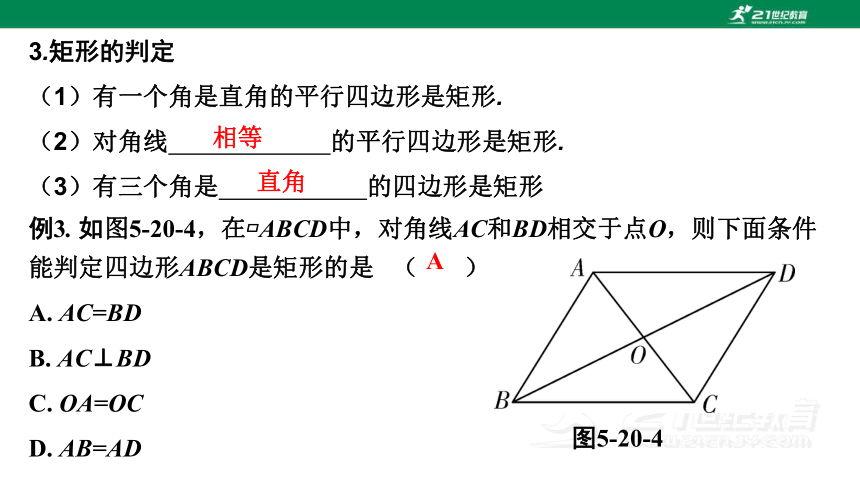
3.矩形的判定
(1)有一个角是直角的平行四边形是矩形.
(2)对角线 的平行四边形是矩形.
(3)有三个角是 的四边形是矩形
相等
直角
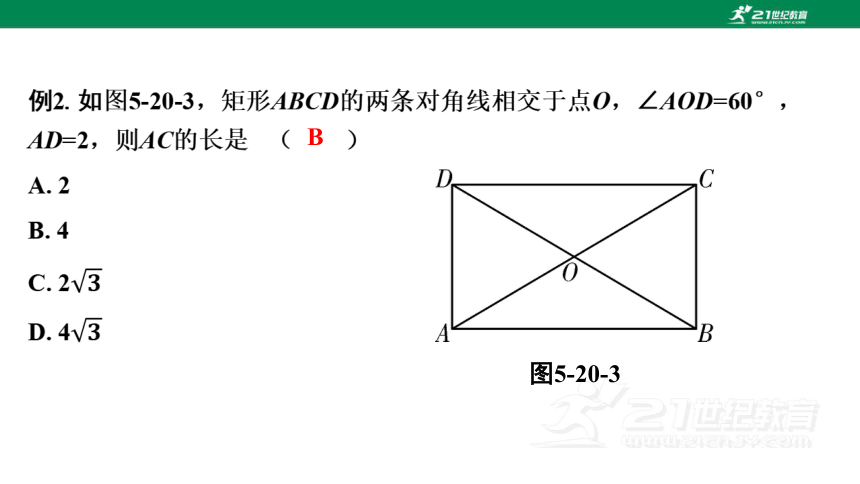
例3. 如图5-20-4,在 ABCD中,对角线AC和BD相交于点O,则下面条件能判定四边形ABCD是矩形的是 ( )
A. AC=BD
B. AC⊥BD
C. OA=OC
D. AB=AD
图5-20-4
A
4.菱形的概念
有一组邻边 的平行四边形叫做菱形
例4. 下面四个定义中不正确的是 ( )
A.有一个角是直角的平行四边形叫做矩形
B.有一组邻边相等的四边形叫做菱形
C.有一组邻边相等,并且有一个角是直角的平行四边形叫做正方形
D.有一组邻边相等的平行四边形叫做菱形
相等
B
5.菱形的性质
(1)具有平行四边形的所有性质.
(2)菱形的四条边都 .
(3)菱形的对角线互相 ,每条对角线平分一组对角.
(4)菱形既是中心对称图形,也是轴对称图形,有 条对称轴
相等
垂直
2
例5. 在菱形ABCD中,AC,BD为对角线,下列说法一定正确的是( )
A. AC=BD
B. AC⊥BD
C.∠ABD=∠BAC
D.∠BAC+∠CAD=90°
B
6.菱形的判定
(1)有一组邻边相等的平行四边形是菱形.
(2)四条边 的四边形是菱形.
(3)对角线互相 的平行四边形是菱形
相等
垂直
例6. 如图5-20-5,下列选项中,能证明 ABCD是菱形的条件有 ( )
① AC⊥BD;② BA⊥AD;③ AB=BC;④ AC=BD.
A. ①②③ B. ②③
C. ③④ D. ①③
图5-20-5
D
7.正方形的概念
有一组邻边 ,并且有一个角是 的平行四边形叫做正方形
例7. 在四边形ABCD中,AB∥CD,∠B=∠D,∠A=90°,如果添加一个条件,即可推出该四边形是正方形,那么这个条件可以是 ( )
A. ∠D=90° B. AB=CD
C. BC=CD D. AC=BD
相等
直角
C
8.正方形的性质
正方形具有矩形和菱形的性质:
(1)边:四条边都 ,对边平行.
(2)角:四个角都是 .
(3)对角线:对角线相等且 ,每条对角线 一组对角.
(4)正方形既是中心对称图形,也是轴对称图形,有 条对称轴
相等
直角
互相垂直平分
平分
4
例8. 如图5-20-6,四边形ABCD是正方形,对角线AC,BD交于点O.下列结论:① OA=OB;② ∠ACB=45°;③ AC⊥BD;④正方形ABCD有4条对称轴.上述结论正确的有 ( )
A. ①②③④ B. ①②③
C. ②③④ D. ①③④
图5-20-6
A
9.正方形的判定
(1)有一组邻边 的矩形是正方形.
(2)对角线互相 的矩形是正方形.
(3)有一个角是 的菱形是正方形.
(4)对角线 的菱形是正方形
相等
垂直
直角
相等
例9. (1)在矩形ABCD中,对角线AC,BD交于点O,要使该矩形成为正方形,可添加的一个条件是 ;
(2)在菱形ABCD中,对角线AC,BD交于点O,要使该菱形成为正方形,可添加的一个条件是 .
AB=AD(答案不唯一)
AC=BD(答案不唯一)
10.平行四边形、矩形、菱形与正方形的关系
(1)从边、角分析:
(2)从对角线分析:
例10. 如图5-20-7,已知 ABCD的对角线AC与BD相交于点O,请你添加两个适当的条件: ,使 ABCD变为正方形.
图5-20-7
AB=BC,∠ABC=90°(答案不唯一)
11.梯形的概念
只有一组对边 的四边形叫做梯形.其中有一个角是直角的梯形叫做 梯形,两腰相等的梯形叫做 梯形
平行
直角
等腰
例11.如图5-20-8,在梯形ABCD中,AD∥BC,AD=3,AB=CD=4,∠A=120°,则下底BC的长为 .
图5-20-8
7
广东中考
1. (2022·广东题13,3分,菱形的性质)菱形的边长为5,则它的周长是
.
2. (2024·广东题15,3分,菱形的性质;三角形的面积)如图5-20-9,菱形ABCD的面积为24,E是AB的中点,F是BC上的动点. 若△BEF的面积为4,则图中阴影部分的面积为 .
图5-20-9
20
10
高分击破
【典型考点】矩形的判定与性质 得分点分析
1. (2024·兰州)如图5-20-10,在△ABC中,AB=AC,D是BC的中点,CE∥AD,AE⊥AD,EF⊥AC.
图5-20-10
(1)求证:四边形ADCE是矩形;
(1)证明:∵AB=AC,D是BC的中点,
∴AD⊥BC,即∠ADC=∠ADB=90°.
············1分(利用三线合一的性质得1分)
∵CE∥AD,∴∠ECD=∠ADB=90°. ··················2分(利用平行线的性质得1分)
∵AE⊥AD,∴∠EAD=90°. ··································3分(利用垂直的定义得1分)
∴∠ADC=∠ECD=∠EAD=90°.∴四边形ADCE是矩形. ··················4分(利用矩形的判定得1分)
图5-20-10
(2)若BC=4,CE=3,求EF的长.
图5-20-10
温馨提示:此类考题可能见于广东省中考数学试卷的第19题,分值一般为9分,答题时要注意书写格式,分步书写,慢做会求全对,评卷老师是分步给分的哦!
【典型错例】重复证明的错误
2. 如图5-20-11, ABCD的对角线AC的垂直平分线与边AD,BC分别相交于点E,F. 求证:四边形AFCE是菱形.
图5-20-11
错解分析
错解:∵四边形ABCD是平行四边形,
∴AD∥BC.∴∠EAO=∠FCO.
∵EF垂直平分AC,
∴AE=CE,AF=CF,AO=CO,EF⊥AC.
又∵∠AOE=∠COF,∴△AOE≌△COF(ASA).
∴AE=CF,OE=OF.∴AE=CE=CF=AF,AC与EF互相垂直平分.
∴四边形AFCE是菱形.
剖析:该解题过程犯了重复证明的错误,在证明四边相等后,又证明了对角线互相垂直平分,这两组条件都可以判定菱形,选其中一个即可.
图5-20-11
【生长式训练】知识生长→变式创新
3. (中考创新,原创题)如图5-20-12①,将矩形纸片ABCD沿对角线AC剪开,得到△ABC和△ACD,并且测得AB=3 cm,BC=4 cm.
图5-20-12
知识种子:基本概念
(1)将这两张三角形纸片按图5-20-12②的方式摆放,连接BD,则AC与BD的位置关系是 ;
图5-20-12
AC⊥BD
种子生长:矩形的判定与性质
(2)如图5-20-12③,将图5-20-12②中的△A'C'D纸片沿射线CA方向平移,连接BC',BA',直至BC'∥A'D.
①判断四边形A'BC'D的形状,并说明理由;
解:①四边形A'BC'D是矩形.
理由:如图5-20-12①,
在矩形ABCD中,∠D=90°,AD=BC,AD∥BC,
∴∠ACB=∠CAD.
∴在图5-20-12③中,BC=A'D,∠ACB=∠C'A'D,∠D=90°.
∵BC'∥A'D,∴∠C'A'D=∠A'C'B.
∴∠A'C'B=∠ACB.∴BC'=BC.
∴BC'=A'D.∴四边形A'BC'D是平行四边形.
又∵∠D=90°,∴四边形A'BC'D是矩形.
图5-20-12
答图5-20-1
②求平移的距离AC';
生长变式:图形变式
(3)如图5-20-13,将图5-20-12①中的△ACD以点A为旋转中心,按逆时针方向旋转∠α,使∠α=∠BAC,得到△AC'D,过点C作AC'的平行线,与DC'的延长线交于点E,判定四边形ACEC'的形状,并说明理由;
解:四边形ACEC'是菱形.
理由:如图5-20-12①,在矩形ABCD中,AB∥CD ∴∠ACD=∠BAC.
如图5-20-13,由旋转的性质,得AC'=AC,∠AC'D=∠BAC.
∵∠CAC'=∠α,∠α=∠BAC,
∴∠CAC'=∠AC'D.∴AC∥C'E.
又∵CE∥AC',∴四边形ACEC'是平行四边形.
又∵AC'=AC,∴四边形ACEC'是菱形.
图5-20-13
种子成树:综合创新
(4)如图5-20-14①,将图5-20-13中的△AC'D继续按逆时针方向旋转,使B,A,D三点在同一条直线上,连接CC',取CC'的中点F,连接AF并延长至点G,使FG=AF,连接CG,C'G.
图5-20-14
①判断四边形ACGC'的形状,并说明理由;
解:①四边形ACGC'是正方形.
理由:∵F为CC'的中点,∴C'F=CF.
又∵FG=AF,∴四边形ACGC'是平行四边形.
又∵AC=AC',∴四边形ACGC'是菱形.
∵∠AC'D=∠BAC,∠AC'D+∠DAC'=90°,
∴∠BAC+∠DAC'=90°.
∴∠CAC'=180°-(∠BAC+∠DAC')=90°.
∴四边形ACGC'是正方形.
图5-20-14
②如图5-20-14②,将图5-20-14①中△ABC沿着BD方向平移,使点B与点A重合,此时点A平移至点A',A'C与BC'交于点P,连接CC',求tan∠C'CP的值.
图5-20-14
中考演练
(限时15分钟)
一、选择题
1. (2024·成都)如图5-20-15,在矩形ABCD中,对角线AC与BD相交于点O,则下列结论一定正确的是 ( )
A. AB=AD
B. AC⊥BD
C. AC=BD
D. ∠ACB=∠ACD
图5-20-15
C
图5-20-16
C
3. (2024·通辽)如图5-20-17, ABCD的对角线AC,BD交于点O,以下条件不能证明 ABCD是菱形的是 ( )
A. ∠BAC=∠BCA
B. ∠ABD=∠CBD
C. OA2+OB2=AD2
D. AD2+OA2=OD2
图5-20-17
D
图5-20-18
B
图5-20-19
B
二、填空题
6. (2024·甘孜州)如图5-20-20,在菱形ABCD中,AB=2,则菱形ABCD的周长为 .
图5-20-20
8
7. (2024·兰州)如图5-20-21,四边形ABCD为正方形,△ADE为等边三角形,EF⊥AB于点F.若AD=4,则EF= .
图5-20-21
2
8. (2023·陕西)如图5-20-22,在矩形ABCD中,AB=3,BC=4.点E在边AD上,且ED=3,M,N分别是边AB,BC上的动点,且BM=BN,P是线段CE上的动点,连接PM,PN.若PM+PN=4,则线段PC的长为 .
图5-20-22
三、解答题
9. (2024·广安)如图5-20-23,菱形ABCD中,E,F分别是边AB,BC上的点,BE=BF,求证:∠DEF=∠DFE.
图5-20-23
10. (2024·长沙)如图5-20-24,在 ABCD中,对角线AC,BD相交于点O,∠ABC=90°.
(1)求证:AC=BD;
图5-20-24
(1)证明:∵四边形ABCD是平行四边形,∠ABC=90°,
∴四边形ABCD是矩形.∴AC=BD.
(2)点E在BC边上,满足∠CEO=∠COE. 若AB=6,BC=8,求CE的长及tan∠CEO的值.
答图5-20-2
命题趋势
( 限时 5 分钟)
图5-20-25
【知识技能】 (1)如图5-20-25①,当OE⊥AC时,G,Q,C三点重合,此时OQ与OP的数量关系为 ;
图5-20-25
【数学理解】(2)当正方形OEFG旋转到如图5-20-25②所示的位置时,猜想OQ与OP的数量关系,并说明理由;
答图5-20-3
答图5-20-3
【拓展探索】(3)在正方形的旋转过程中,
当DE=EF时,请直接写出DF的长.
答图5-20-4
答图5-20-5
命题解读:根据最新课程标准和近三年中考命题动向,预测2025年中考命题方向可能注重考查特殊四边形的基本概念、性质和判定方法,如通过具体图形判断它们的类型、计算相关角度或边长等;强调与其他几何图形的综合运用,可能与三角形、平行四边形、圆等结合;还可能会考查综合探究类题型,通过变换图形位置或构造特殊图形综合考查.
同课章节目录
