中考数学复习知识梳理第三章函数第9课时平面直角坐标系与函数课件(共50张PPT)
文档属性
| 名称 | 中考数学复习知识梳理第三章函数第9课时平面直角坐标系与函数课件(共50张PPT) |  | |
| 格式 | ppt | ||
| 文件大小 | 4.1MB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 通用版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2025-05-31 09:35:05 | ||
图片预览









文档简介
(共50张PPT)
第三章 函 数
第9课时 平面直角坐标系与函数
课前循环练
(限时5分钟)
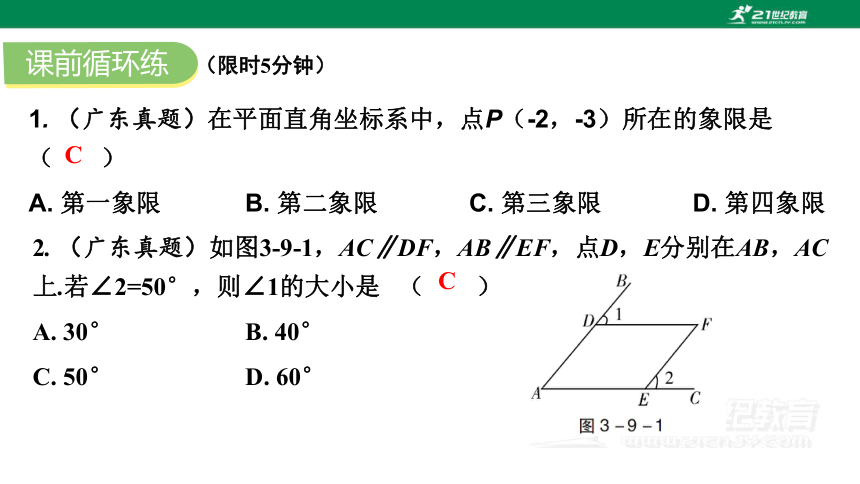
1. (广东真题)在平面直角坐标系中,点P(-2,-3)所在的象限是 ( )
A. 第一象限 B. 第二象限 C. 第三象限 D. 第四象限
C
2. (广东真题)如图3-9-1,AC∥DF,AB∥EF,点D,E分别在AB,AC上.若∠2=50°,则∠1的大小是 ( )
A. 30° B. 40°
C. 50° D. 60°
C
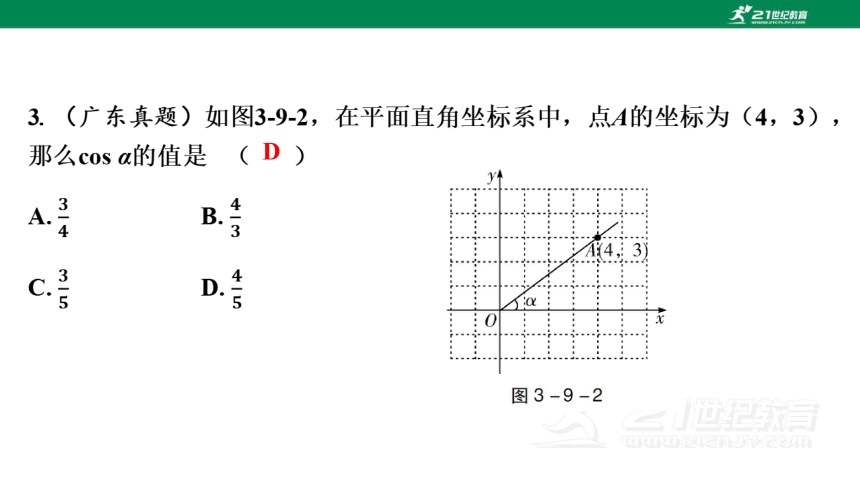
D
4. (广东真题)袋中有同样大小的4个小球,其中3个红色,1个白色. 从袋中任意摸出两个球,这两个球颜色相同的概率是 .
5. (广东真题)如图3-9-3,三个小正方形的边长都为1,则图中阴影部分
面积的和是 .(结果保留π)
(1)平面直角坐标系
①理解平面直角坐标系的有关概念,能画出平面直角坐标系;在给定的平面直角坐标系中,能根据坐标描出点的位置,由点的位置写出坐标.
②在实际问题中,能建立适当的平面直角坐标系,描述物体的位置.
③对给定的正方形,会选择合适的平面直角坐标系,写出它的顶点坐标,体会可以用坐标表达简单图形.
课标要求
④在平面直角坐标系中,以坐标轴为对称轴,能写出一个已知顶点坐标的多边形的对称图形的顶点坐标,知道对应顶点坐标之间的关系.
⑤在平面直角坐标系中,能写出一个已知顶点坐标的多边形沿坐标轴方向平移一定距离后图形的顶点坐标,知道对应顶点坐标之间的关系.
⑥在平面直角坐标系中,探索并了解将一个多边形依次沿两个坐标轴方向平移后所得到的图形和原来图形具有平移关系,体会图形顶点坐标的变化.
(2)函数
①探索简单实例中的数量关系和变化规律,了解常量、变量的意义;了解函数的概念和表示法,能举出函数的实例.
②能结合图象对简单实际问题中的函数关系进行分析.
③能确定简单实际问题中函数自变量的取值范围,会求函数值.
④能用适当的函数表示法刻画简单实际问题中变量之间的关系,理解函数值的意义.
⑤结合对函数关系的分析,能对变量的变化情况进行初步讨论.
对接教材 人教:七下第七章 平面直角坐标系;八下第十九章 一次函数(19.1函数)
北师:七下第三章 变量之间的关系;八上第三章 位置与坐标;
八上第四章 一次函数(4.1函数)
考点梳理
考点复习
1.平面直角坐标系
在平面内,两条互相 且有公共 的数轴组成平面直角坐标系.平面直角坐标系中的点和有序实数对是 对应的
垂直
原点
一一
广东省对应考点例题
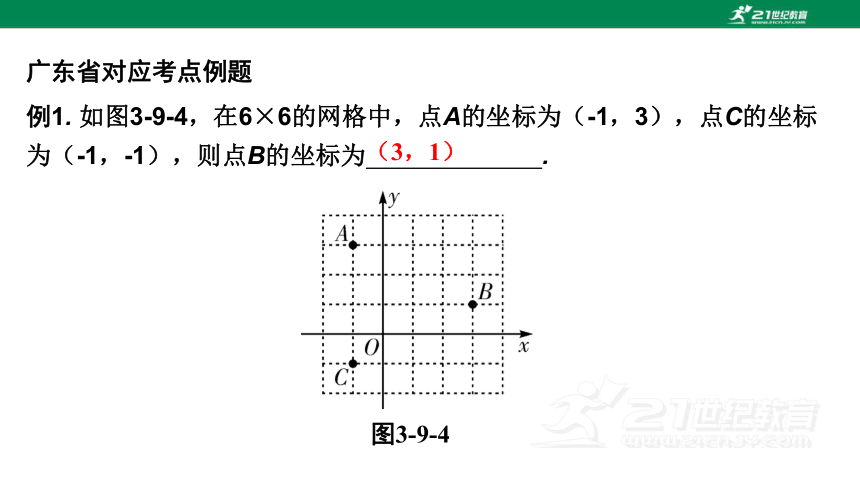
例1. 如图3-9-4,在6×6的网格中,点A的坐标为(-1,3),点C的坐标为(-1,-1),则点B的坐标为 .
图3-9-4
(3,1)
2.各象限内点的坐标特征(如图3-9-5)
(1)若点P(a,b)在第一象限,则a>0,b>0.
(2)若点P(a,b)在第二象限,则a 0,b 0.
(3)若点P(a,b)在第三象限,则a 0,b 0.
(4)若点P(a,b)在第四象限,则a 0,b 0.
(5)坐标轴上的点不属于任何象限
图3-9-5
<
>
<
<
>
<
例2. 如果点P(m+3,4)在第二象限,那么点Q(m-3,m)的位置在
( )
A.第一象限
B.第二象限
C.第三象限
D.第四象限
C
3.与坐标轴有关的点的坐标特征
(1)坐标轴上点的坐标特征:
①x轴上的点的 为0;
②y轴上的点的 为0;
③原点的坐标为 .
(2)平行于坐标轴的直线上点的坐标特征:
①平行于x轴的直线上的点的 相同;
②平行于y轴的直线上的点的 相同
纵坐标
横坐标
(0,0)
纵坐标
横坐标
例3. 如图3-9-6,将 ABCO放置在平面直角坐标系xOy中,O为坐标原点.若点A的坐标是(6,0),点C的坐标是(1,4),则点B的坐标是
.
图3-9-6
(7,4)
4.对称点的坐标特征
点P(a,b)关于x轴的对称点P1的坐标为 ;
点P(a,b)关于y轴的对称点P2的坐标为 ;
点P(a,b)关于原点的对称点P3的坐标为
(a,-b)
(-a,b)
(-a,-b)
例4. 在平面直角坐标系中,点P(3,-2)关于y轴的对称点的坐标是
,关于x轴的对称点的坐标是 ,关于原点的对称点的坐标是 .
(-3,-2)
(3,2)
(-3,2)
5.点的坐标平移变化规律
(1)点(a,b)向右平移m个单位长度可得到点(a+m,b);点(a,b)向左平移m个单位长度可得到点(a-m,b);点(a,b)向上平移n个单位长度可得到点(a,b+n);点(a,b)向下平移n个单位长度可得到点(a,b-n).
(2)根据其规律可得口诀:左右平移→左减右加纵不变;上下平移→上加下减横不变
例5. 在平面直角坐标系中,将点(-4,-6)先向右平移4个单位长度,再向上平移6个单位长度得到点A,则点A的坐标为 .
(0,0)
6.坐标与距离
点P(a,b)到x轴的距离为 ,到y轴的距离为 ,到原点的距离为
例6. 已知点P在第四象限,且到x轴的距离是3,到y轴的距离是2,则点P的坐标为 .
(2,-3)
7.函数的有关概念
(1)变量与常量:在一个变化过程中,我们称数值发生变化的量为变量,数值始终不变的量为常量.
(2)函数的概念:一般地,在一个变化过程中,如果有两个变量x与y,并且对于x的每一个确定的值,y都有唯一确定的值与其对应,那么我们就说x是自变量,y是x的函数.
(3)表示方法: 法、 法、 法.
解析式
列表
图象
(4)自变量的取值范围
(5)函数值:对于一个函数,如果当x=a时y=b,那么b就叫做当自变量的值为a时的函数值
解析式 自变量的取值范围
整式型:y=x
分母 的实数
被开方数为 的实数
全体实数
不为0
非负数
9π
36π
半径r
面积S
全体实数
x≠2
x≤3
3
8.函数的图象
(1)函数图象的概念:一般地,对于一个函数,如果把自变量与函数的每对对应值分别作为点的横、纵坐标,那么坐标平面内由这些点组成的图形,就是这个函数的图象.
(2)描点法画函数图象的一般步骤:列表、描点、连线
例8.小明从家出发步行至学校,停留一段时间后乘车返回,则下列函数图象最能体现他离家的距离s与出发时间t之间的对应关系的是 ( )
B
广东中考
1. (2022·广东题10,3分,常量与变量)水中涟漪(圆形水波)不断扩大,记它的半径为r,则圆周长C与r的关系式为C=2πr. 下列判断正确的是 ( )
A. 2是变量 B.π是变量 C. r是变量 D. C是常量
2. (2020·广东题3,3分,对称点的坐标)在平面直角坐标系中,点(3,2)关于x轴对称的点的坐标为 ( )
A. (-3,2) B. (-2,3) C. (2,-3) D. (3,-2)
C
D
3. (2022·广东题6,3分,点的坐标平移)在平面直角坐标系中,将点(1,1)向右平移2个单位长度后,得到的点的坐标是 ( )
A. (3,1) B. (-1,1)
C. (1,3) D. (1,-1)
A
4. (2022·广东题20,9分,函数的表示方法;函数值)物理实验证实:在弹性限度内,某弹簧长度y(cm)与所挂物体质量x(kg)满足函数关系y=kx+15. 下表是测量物体质量时,该弹簧长度y与所挂物体质量x的数量关系.
x/kg 0 2 5
y/cm 15 19 25
(1)求y与x的函数关系式;
解:(1)把x=2,y=19代入y=kx+15,得2k+15=19.
解得k=2.
∴y与x的函数关系式为y=2x+15.
(2)当弹簧长度为20 cm时,求所挂物体的质量.
(2)把y=20代入y=2x+15,得2x+15=20.
解得x=2.5.
∴当弹簧长度为20 cm时,所挂物体的质量为2.5 kg.
高分击破
【典型考点】函数的三种表示方法(列表法、图象法、解析式法) 得分点分析
1. (2024·广州)一个人的脚印信息往往对应着这个人某些方面的基本特征.某数学兴趣小组收集了大量不同人群的身高和脚长数据,通过对数据的整理和分析,发现身高y和脚长x之间近似存在一种函数关系,部分数据如表:
脚长x/cm … 23 24 25 26 27 28 …
身高y/cm … 156 163 170 177 184 191 …
(1)在图3-9-7①中描出表中数据对应的点(x,y);
解:(1)描点如图3-9-8. ····································3分(描点得3分)
(3)如图3-9-7②,某场所发现了一个人的脚印,脚长约为25.8 cm,请根据(2)中求出的函数解析式,估计这个人的身高.
(3)把x=25.8代入y=7x-5,得
y=7×25.8-5=175.6. ········································ 8分(代入求函数值得1分)
∴估计这个人的身高为175.6 cm. ······························9分(答数得1分)
温馨提示:此类考题可能见于广东省中考数学试卷的第20题,分值一般为9分,答题时要注意书写规范,分步书写,慢做会求全对,评卷老师是分步给分的哦!
【典型错例】不会用绝对值表示距离和分类讨论
2. 已知点P(2-m,2m+6),且点P到两坐标轴的距离相等,求点P的坐标.
【生长式训练】知识生长→变式创新
3. (中考创新,原创题)已知点P(1-3m,2-n),Q(m-3,2n+5).
知识种子:基本概念
(1)若点P在x轴上,点Q在y轴上,则m= ,n= ;
3
2
种子生长:点的坐标特征
(2)若PQ∥y轴,且PQ=6,求m,n的值;
生长变式:坐标变式
(3)点P和点Q是否能同时在第三象限内?若能,求出m,n的取值范围;若不能,请说明理由;
种子成树:综合创新
(4)定义:若点A(x,y)满足y=2x+17,则称点A为“能量点”. 已知点P,Q均为“能量点”,求m,n的值.
中考演练
(限时15分钟)
一、选择题
1. (2024·资阳)在平面直角坐标系中,将点(-2,1)沿y轴向上平移1个单位长度后,得到的点的坐标为 ( )
A. (-2,0) B. (-2,2) C. (-3,1) D. (-1,1)
2. (2024·凉山州)点P(a,-3)关于原点对称的点是P'(2,b),则a+b的值是 ( )
A. 1 B. -1 C. -5 D. 5
B
A
3. (2024·广西)如图3-9-9,在平面直角坐标系中,点O为坐标原点,点P的坐标为(2,1),则点Q的坐标为 ( )
A. (3,0)
B. (0,2)
C. (3,2)
D. (1,2)
C
4. (2024·贵州)为培养青少年的科学态度和科学思维,某校创建了“科技创新”社团. 小红将“科”“技”“创”“新”写在如图3-9-10所示的方格纸中.若建立平面直角坐标系,使“创”“新”的坐标分别为(-2,0),(0,0),则“技”所在的象限为 ( )
A. 第一象限
B. 第二象限
C. 第三象限
D. 第四象限
A
5. (2024·江西)将常温中的温度计插入一杯60 ℃的热水(恒温)中,温度计的读数y(℃)与时间x(min)的关系用图象可近似表示为( )
C
三
(-5,-1)
x≥3
三、解答题
9. (教材改编)已知点P(2m+4,m-1),试分别根据下列条件,求出点P的坐标.
(1)点P在y轴上;
解:(1)由题意,得2m+4=0.解得m=-2.
∴m-1=-3.
∴点P的坐标为(0,-3).
(2)点P在过点A(2,-4)且与x轴平行的直线上;
(2)由题意,得m-1=-4.解得m=-3.
∴2m+4=-2.
∴点P的坐标为(-2,-4).
(3)点P到两坐标轴的距离相等.
10. (教材改编)科学家一直以来都在不断探索地球奥秘的路途中,经过大量的模拟实验,发现地表以下岩层的温度y(℃)与所处深度x(km)的关系如下表:
(1)表中,自变量为 ,因变量为 ;
x/km 1 2 3 4 5 6 7
y/℃ 55 90 125 160 195 230 265
所处深度x
岩层的温度y
(2)求y与x的函数关系式;
解:(2)由表格可知,所处深度每增加1 km,岩层的温度就升高35 ℃,
则y=55+35(x-1)=35x+20.
∴y与x的函数关系式为y=35x+20.
(3)当岩层的温度为1 280 ℃时,求所处深度.
(3)把y=1 280代入y=35x+20,得35x+20=1 280.
解得x=36.
∴当岩层的温度为1 280 ℃时,所处深度是36 km.
命题趋势
( 限时 5 分钟)
综合与实践
医生们经过长期临床观察发现,人的情绪从出生之日起呈周期性变化,在前30天内,情绪的部分数据及函数图象如下:
天数t … 20 21 22 23 24 25 26 27 28 29 30
波动值s … 0.3 0 0.3 1 2.2 3.8 5.7 7.8 10 12.7 15
图3-9-11
(1)数学活动:
①根据表中数据,通过描点,连线(光滑曲线)的方式补全该函数的图象;
②观察前30天的函数图象,当t=14时,s的值为多少?当s的值最大时,t的值为多少?
解:(1)①补全该函数的图象如答图3-9-1.
②由图象可知,当t=14时,s的值为10;
当s的值最大时,t的值为7.
答图3-9-1
图3-9-11
(2)数学思考:请结合函数图象,写出该函数的两条性质或结论;
(2)①当7≤t≤21时,s随t的增大而减小;
②变化周期是28天. (答案不唯一)
图3-9-11
(3)数学应用:根据研究,当s>10时处于情绪高潮期,心情愉快;s<10时为情绪低潮期,心情烦躁;s=10时为临界日,心情平稳.若小海从出生到今天的天数为5 501天,则今天他心情如何?
(3)∵周期为28天,5 501÷28=196……13,
∴t=5 501时s的值与t=13时s的值相等.
又∵当t=13时,s>10,
∴当t=5 501时,s>10.
∴今天小海处于情绪高潮期,心情愉快.
图3-9-11
命题解读:根据最新课程标准和近三年中考命题动向,预测2025年中考命题方向可能注重考查平面直角坐标系与函数的有关概念,如点的坐标、象限、平移、对称、常量与变量等;强调函数的表示方法和性质,可能通过实际问题情境来考查;可能会出现与几何图形变换相结合的题目,还可能出现涉及新定义运算的创新题型.
第三章 函 数
第9课时 平面直角坐标系与函数
课前循环练
(限时5分钟)
1. (广东真题)在平面直角坐标系中,点P(-2,-3)所在的象限是 ( )
A. 第一象限 B. 第二象限 C. 第三象限 D. 第四象限
C
2. (广东真题)如图3-9-1,AC∥DF,AB∥EF,点D,E分别在AB,AC上.若∠2=50°,则∠1的大小是 ( )
A. 30° B. 40°
C. 50° D. 60°
C
D
4. (广东真题)袋中有同样大小的4个小球,其中3个红色,1个白色. 从袋中任意摸出两个球,这两个球颜色相同的概率是 .
5. (广东真题)如图3-9-3,三个小正方形的边长都为1,则图中阴影部分
面积的和是 .(结果保留π)
(1)平面直角坐标系
①理解平面直角坐标系的有关概念,能画出平面直角坐标系;在给定的平面直角坐标系中,能根据坐标描出点的位置,由点的位置写出坐标.
②在实际问题中,能建立适当的平面直角坐标系,描述物体的位置.
③对给定的正方形,会选择合适的平面直角坐标系,写出它的顶点坐标,体会可以用坐标表达简单图形.
课标要求
④在平面直角坐标系中,以坐标轴为对称轴,能写出一个已知顶点坐标的多边形的对称图形的顶点坐标,知道对应顶点坐标之间的关系.
⑤在平面直角坐标系中,能写出一个已知顶点坐标的多边形沿坐标轴方向平移一定距离后图形的顶点坐标,知道对应顶点坐标之间的关系.
⑥在平面直角坐标系中,探索并了解将一个多边形依次沿两个坐标轴方向平移后所得到的图形和原来图形具有平移关系,体会图形顶点坐标的变化.
(2)函数
①探索简单实例中的数量关系和变化规律,了解常量、变量的意义;了解函数的概念和表示法,能举出函数的实例.
②能结合图象对简单实际问题中的函数关系进行分析.
③能确定简单实际问题中函数自变量的取值范围,会求函数值.
④能用适当的函数表示法刻画简单实际问题中变量之间的关系,理解函数值的意义.
⑤结合对函数关系的分析,能对变量的变化情况进行初步讨论.
对接教材 人教:七下第七章 平面直角坐标系;八下第十九章 一次函数(19.1函数)
北师:七下第三章 变量之间的关系;八上第三章 位置与坐标;
八上第四章 一次函数(4.1函数)
考点梳理
考点复习
1.平面直角坐标系
在平面内,两条互相 且有公共 的数轴组成平面直角坐标系.平面直角坐标系中的点和有序实数对是 对应的
垂直
原点
一一
广东省对应考点例题
例1. 如图3-9-4,在6×6的网格中,点A的坐标为(-1,3),点C的坐标为(-1,-1),则点B的坐标为 .
图3-9-4
(3,1)
2.各象限内点的坐标特征(如图3-9-5)
(1)若点P(a,b)在第一象限,则a>0,b>0.
(2)若点P(a,b)在第二象限,则a 0,b 0.
(3)若点P(a,b)在第三象限,则a 0,b 0.
(4)若点P(a,b)在第四象限,则a 0,b 0.
(5)坐标轴上的点不属于任何象限
图3-9-5
<
>
<
<
>
<
例2. 如果点P(m+3,4)在第二象限,那么点Q(m-3,m)的位置在
( )
A.第一象限
B.第二象限
C.第三象限
D.第四象限
C
3.与坐标轴有关的点的坐标特征
(1)坐标轴上点的坐标特征:
①x轴上的点的 为0;
②y轴上的点的 为0;
③原点的坐标为 .
(2)平行于坐标轴的直线上点的坐标特征:
①平行于x轴的直线上的点的 相同;
②平行于y轴的直线上的点的 相同
纵坐标
横坐标
(0,0)
纵坐标
横坐标
例3. 如图3-9-6,将 ABCO放置在平面直角坐标系xOy中,O为坐标原点.若点A的坐标是(6,0),点C的坐标是(1,4),则点B的坐标是
.
图3-9-6
(7,4)
4.对称点的坐标特征
点P(a,b)关于x轴的对称点P1的坐标为 ;
点P(a,b)关于y轴的对称点P2的坐标为 ;
点P(a,b)关于原点的对称点P3的坐标为
(a,-b)
(-a,b)
(-a,-b)
例4. 在平面直角坐标系中,点P(3,-2)关于y轴的对称点的坐标是
,关于x轴的对称点的坐标是 ,关于原点的对称点的坐标是 .
(-3,-2)
(3,2)
(-3,2)
5.点的坐标平移变化规律
(1)点(a,b)向右平移m个单位长度可得到点(a+m,b);点(a,b)向左平移m个单位长度可得到点(a-m,b);点(a,b)向上平移n个单位长度可得到点(a,b+n);点(a,b)向下平移n个单位长度可得到点(a,b-n).
(2)根据其规律可得口诀:左右平移→左减右加纵不变;上下平移→上加下减横不变
例5. 在平面直角坐标系中,将点(-4,-6)先向右平移4个单位长度,再向上平移6个单位长度得到点A,则点A的坐标为 .
(0,0)
6.坐标与距离
点P(a,b)到x轴的距离为 ,到y轴的距离为 ,到原点的距离为
例6. 已知点P在第四象限,且到x轴的距离是3,到y轴的距离是2,则点P的坐标为 .
(2,-3)
7.函数的有关概念
(1)变量与常量:在一个变化过程中,我们称数值发生变化的量为变量,数值始终不变的量为常量.
(2)函数的概念:一般地,在一个变化过程中,如果有两个变量x与y,并且对于x的每一个确定的值,y都有唯一确定的值与其对应,那么我们就说x是自变量,y是x的函数.
(3)表示方法: 法、 法、 法.
解析式
列表
图象
(4)自变量的取值范围
(5)函数值:对于一个函数,如果当x=a时y=b,那么b就叫做当自变量的值为a时的函数值
解析式 自变量的取值范围
整式型:y=x
分母 的实数
被开方数为 的实数
全体实数
不为0
非负数
9π
36π
半径r
面积S
全体实数
x≠2
x≤3
3
8.函数的图象
(1)函数图象的概念:一般地,对于一个函数,如果把自变量与函数的每对对应值分别作为点的横、纵坐标,那么坐标平面内由这些点组成的图形,就是这个函数的图象.
(2)描点法画函数图象的一般步骤:列表、描点、连线
例8.小明从家出发步行至学校,停留一段时间后乘车返回,则下列函数图象最能体现他离家的距离s与出发时间t之间的对应关系的是 ( )
B
广东中考
1. (2022·广东题10,3分,常量与变量)水中涟漪(圆形水波)不断扩大,记它的半径为r,则圆周长C与r的关系式为C=2πr. 下列判断正确的是 ( )
A. 2是变量 B.π是变量 C. r是变量 D. C是常量
2. (2020·广东题3,3分,对称点的坐标)在平面直角坐标系中,点(3,2)关于x轴对称的点的坐标为 ( )
A. (-3,2) B. (-2,3) C. (2,-3) D. (3,-2)
C
D
3. (2022·广东题6,3分,点的坐标平移)在平面直角坐标系中,将点(1,1)向右平移2个单位长度后,得到的点的坐标是 ( )
A. (3,1) B. (-1,1)
C. (1,3) D. (1,-1)
A
4. (2022·广东题20,9分,函数的表示方法;函数值)物理实验证实:在弹性限度内,某弹簧长度y(cm)与所挂物体质量x(kg)满足函数关系y=kx+15. 下表是测量物体质量时,该弹簧长度y与所挂物体质量x的数量关系.
x/kg 0 2 5
y/cm 15 19 25
(1)求y与x的函数关系式;
解:(1)把x=2,y=19代入y=kx+15,得2k+15=19.
解得k=2.
∴y与x的函数关系式为y=2x+15.
(2)当弹簧长度为20 cm时,求所挂物体的质量.
(2)把y=20代入y=2x+15,得2x+15=20.
解得x=2.5.
∴当弹簧长度为20 cm时,所挂物体的质量为2.5 kg.
高分击破
【典型考点】函数的三种表示方法(列表法、图象法、解析式法) 得分点分析
1. (2024·广州)一个人的脚印信息往往对应着这个人某些方面的基本特征.某数学兴趣小组收集了大量不同人群的身高和脚长数据,通过对数据的整理和分析,发现身高y和脚长x之间近似存在一种函数关系,部分数据如表:
脚长x/cm … 23 24 25 26 27 28 …
身高y/cm … 156 163 170 177 184 191 …
(1)在图3-9-7①中描出表中数据对应的点(x,y);
解:(1)描点如图3-9-8. ····································3分(描点得3分)
(3)如图3-9-7②,某场所发现了一个人的脚印,脚长约为25.8 cm,请根据(2)中求出的函数解析式,估计这个人的身高.
(3)把x=25.8代入y=7x-5,得
y=7×25.8-5=175.6. ········································ 8分(代入求函数值得1分)
∴估计这个人的身高为175.6 cm. ······························9分(答数得1分)
温馨提示:此类考题可能见于广东省中考数学试卷的第20题,分值一般为9分,答题时要注意书写规范,分步书写,慢做会求全对,评卷老师是分步给分的哦!
【典型错例】不会用绝对值表示距离和分类讨论
2. 已知点P(2-m,2m+6),且点P到两坐标轴的距离相等,求点P的坐标.
【生长式训练】知识生长→变式创新
3. (中考创新,原创题)已知点P(1-3m,2-n),Q(m-3,2n+5).
知识种子:基本概念
(1)若点P在x轴上,点Q在y轴上,则m= ,n= ;
3
2
种子生长:点的坐标特征
(2)若PQ∥y轴,且PQ=6,求m,n的值;
生长变式:坐标变式
(3)点P和点Q是否能同时在第三象限内?若能,求出m,n的取值范围;若不能,请说明理由;
种子成树:综合创新
(4)定义:若点A(x,y)满足y=2x+17,则称点A为“能量点”. 已知点P,Q均为“能量点”,求m,n的值.
中考演练
(限时15分钟)
一、选择题
1. (2024·资阳)在平面直角坐标系中,将点(-2,1)沿y轴向上平移1个单位长度后,得到的点的坐标为 ( )
A. (-2,0) B. (-2,2) C. (-3,1) D. (-1,1)
2. (2024·凉山州)点P(a,-3)关于原点对称的点是P'(2,b),则a+b的值是 ( )
A. 1 B. -1 C. -5 D. 5
B
A
3. (2024·广西)如图3-9-9,在平面直角坐标系中,点O为坐标原点,点P的坐标为(2,1),则点Q的坐标为 ( )
A. (3,0)
B. (0,2)
C. (3,2)
D. (1,2)
C
4. (2024·贵州)为培养青少年的科学态度和科学思维,某校创建了“科技创新”社团. 小红将“科”“技”“创”“新”写在如图3-9-10所示的方格纸中.若建立平面直角坐标系,使“创”“新”的坐标分别为(-2,0),(0,0),则“技”所在的象限为 ( )
A. 第一象限
B. 第二象限
C. 第三象限
D. 第四象限
A
5. (2024·江西)将常温中的温度计插入一杯60 ℃的热水(恒温)中,温度计的读数y(℃)与时间x(min)的关系用图象可近似表示为( )
C
三
(-5,-1)
x≥3
三、解答题
9. (教材改编)已知点P(2m+4,m-1),试分别根据下列条件,求出点P的坐标.
(1)点P在y轴上;
解:(1)由题意,得2m+4=0.解得m=-2.
∴m-1=-3.
∴点P的坐标为(0,-3).
(2)点P在过点A(2,-4)且与x轴平行的直线上;
(2)由题意,得m-1=-4.解得m=-3.
∴2m+4=-2.
∴点P的坐标为(-2,-4).
(3)点P到两坐标轴的距离相等.
10. (教材改编)科学家一直以来都在不断探索地球奥秘的路途中,经过大量的模拟实验,发现地表以下岩层的温度y(℃)与所处深度x(km)的关系如下表:
(1)表中,自变量为 ,因变量为 ;
x/km 1 2 3 4 5 6 7
y/℃ 55 90 125 160 195 230 265
所处深度x
岩层的温度y
(2)求y与x的函数关系式;
解:(2)由表格可知,所处深度每增加1 km,岩层的温度就升高35 ℃,
则y=55+35(x-1)=35x+20.
∴y与x的函数关系式为y=35x+20.
(3)当岩层的温度为1 280 ℃时,求所处深度.
(3)把y=1 280代入y=35x+20,得35x+20=1 280.
解得x=36.
∴当岩层的温度为1 280 ℃时,所处深度是36 km.
命题趋势
( 限时 5 分钟)
综合与实践
医生们经过长期临床观察发现,人的情绪从出生之日起呈周期性变化,在前30天内,情绪的部分数据及函数图象如下:
天数t … 20 21 22 23 24 25 26 27 28 29 30
波动值s … 0.3 0 0.3 1 2.2 3.8 5.7 7.8 10 12.7 15
图3-9-11
(1)数学活动:
①根据表中数据,通过描点,连线(光滑曲线)的方式补全该函数的图象;
②观察前30天的函数图象,当t=14时,s的值为多少?当s的值最大时,t的值为多少?
解:(1)①补全该函数的图象如答图3-9-1.
②由图象可知,当t=14时,s的值为10;
当s的值最大时,t的值为7.
答图3-9-1
图3-9-11
(2)数学思考:请结合函数图象,写出该函数的两条性质或结论;
(2)①当7≤t≤21时,s随t的增大而减小;
②变化周期是28天. (答案不唯一)
图3-9-11
(3)数学应用:根据研究,当s>10时处于情绪高潮期,心情愉快;s<10时为情绪低潮期,心情烦躁;s=10时为临界日,心情平稳.若小海从出生到今天的天数为5 501天,则今天他心情如何?
(3)∵周期为28天,5 501÷28=196……13,
∴t=5 501时s的值与t=13时s的值相等.
又∵当t=13时,s>10,
∴当t=5 501时,s>10.
∴今天小海处于情绪高潮期,心情愉快.
图3-9-11
命题解读:根据最新课程标准和近三年中考命题动向,预测2025年中考命题方向可能注重考查平面直角坐标系与函数的有关概念,如点的坐标、象限、平移、对称、常量与变量等;强调函数的表示方法和性质,可能通过实际问题情境来考查;可能会出现与几何图形变换相结合的题目,还可能出现涉及新定义运算的创新题型.
同课章节目录
