中考数学复习知识梳理第五章四边形第19课时平行四边形课件(共37张PPT)
文档属性
| 名称 | 中考数学复习知识梳理第五章四边形第19课时平行四边形课件(共37张PPT) |  | |
| 格式 | ppt | ||
| 文件大小 | 5.0MB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 通用版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2025-05-31 09:36:53 | ||
图片预览







文档简介
(共37张PPT)
第五章 四 边 形
第19课时 平行四边形
课前循环练
(限时5分钟)
C
C
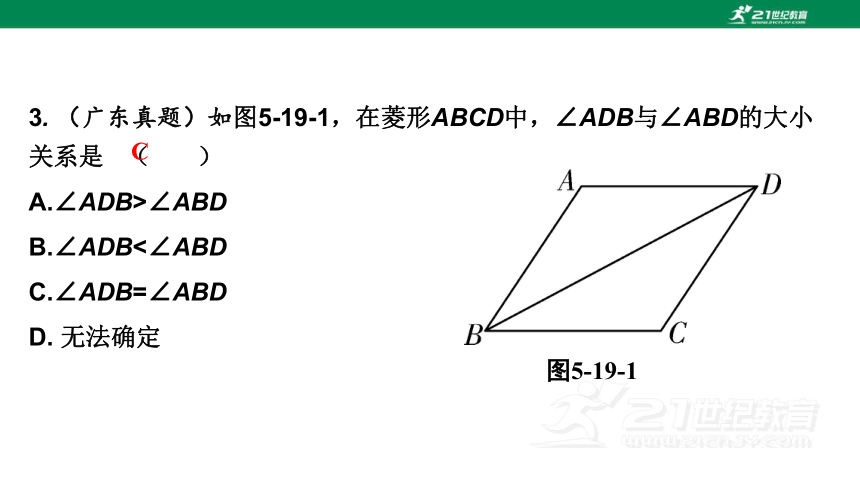
3. (广东真题)如图5-19-1,在菱形ABCD中,∠ADB与∠ABD的大小关系是 ( )
A.∠ADB>∠ABD
B.∠ADB<∠ABD
C.∠ADB=∠ABD
D. 无法确定
图5-19-1
C
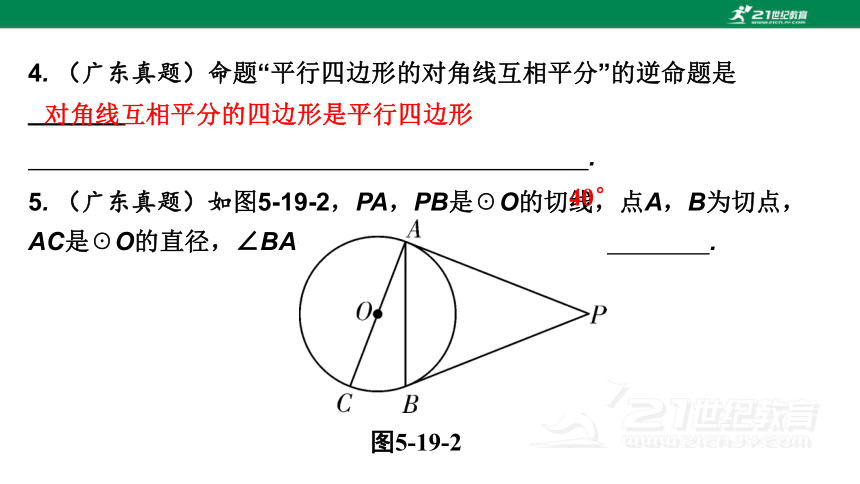
4. (广东真题)命题“平行四边形的对角线互相平分”的逆命题是_______
.
5. (广东真题)如图5-19-2,PA,PB是☉O的切线,点A,B为切点,AC是☉O的直径,∠BAC=20°,则∠P的大小是 .
对角线互相平分的四边形是平行四边形
40°
图5-19-2
①理解平行四边形的概念.
②探索并证明平行四边形的性质定理:平行四边形的对边相等、对角相等、对角线互相平分. 探索并证明平行四边形的判定定理:一组对边平行且相等的四边形是平行四边形;两组对边分别相等的四边形是平行四边形;对角线互相平分的四边形是平行四边形.
③理解两条平行线之间距离的概念,能度量两条平行线之间的距离.
课标要求
对接教材 人教:八下第十八章 平行四边形
北师:八下第六章 平行四边形
考点梳理
考点复习
1.平行四边形的概念
两组对边分别 的四边形叫做平行四边形
平行
广东省对应考点例题
例1. 在 ABCD中,∠A=100°,则∠B= .
80°
2.平行四边形的性质与判定
性质 判定
边 平行四边形的对边 (1)两组对边分别 的四边形是平行四边形;
(2)两组对边分别 的四边形是平行四边形;
(3)一组对边 的四边形是平行四边形
角 平行四边形的对角 两组对角 的四边形是平行四边形
对角
线 平行四边形的对角线_______
对角线 的四边形是平行四边形
对称性 平行四边形是中心对称图形,它的对称中心是
平行且相等
平行
相等
平行且相等
相等
相等
互相
平分
互相平分
对角线的交点
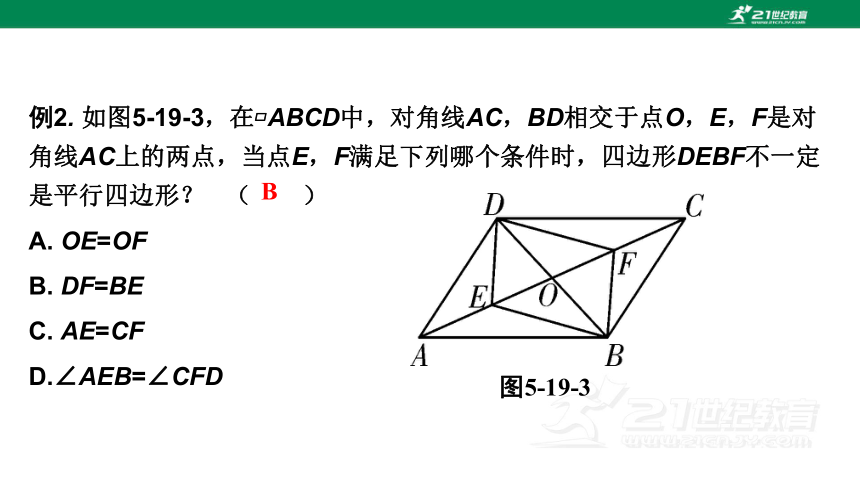
例2. 如图5-19-3,在 ABCD中,对角线AC,BD相交于点O,E,F是对角线AC上的两点,当点E,F满足下列哪个条件时,四边形DEBF不一定是平行四边形? ( )
A. OE=OF
B. DF=BE
C. AE=CF
D.∠AEB=∠CFD
图5-19-3
B
3.平行四边形的面积
(1)平行四边形的面积= .
(2)同底(等底)同高(等高)的平行四边形的面积 .
(3)如果两条直线相互平行,那么其中一条直线上任意一点到另一条直线的距离都相等,这个距离称为平行线之间的距离.平行线间的距离处处
底×高
相等
相等
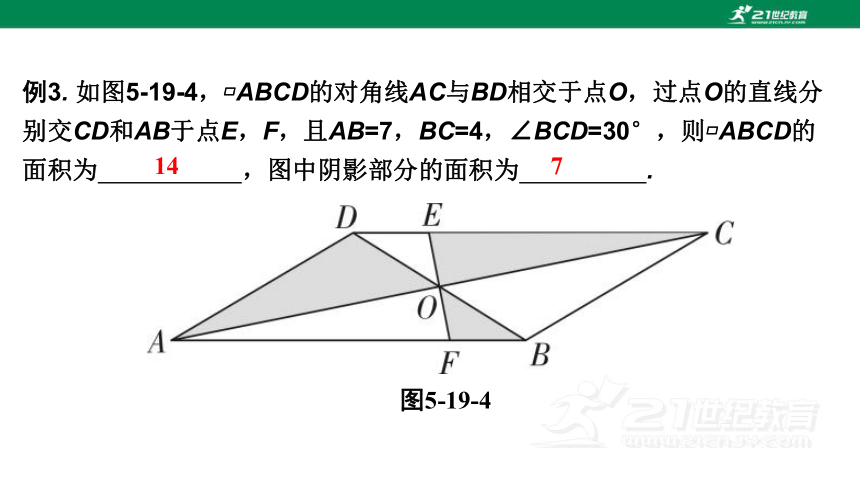
例3. 如图5-19-4, ABCD的对角线AC与BD相交于点O,过点O的直线分别交CD和AB于点E,F,且AB=7,BC=4,∠BCD=30°,则 ABCD的面积为 ,图中阴影部分的面积为 .
图5-19-4
14
7
广东中考
(2022·广东题8,3分,平行四边形的性质)如图5-19-5,在 ABCD中,一定正确的是 ( )
A. AD=CD
B. AC=BD
C. AB=CD
D. CD=BC
图5-19-5
C
高分击破
【典型考点】尺规作图;角平分线的性质;平行四边形的性质 得分点分析
1.如图5-19-6,在 ABCD中,∠A=60°.
(1)实践与操作:用尺规作图法过点B作∠ABC的平分线,交边CD于点E;(保留作图痕迹,不要求写作法)
解:(1)如图5-19-7,BE即为所作. ······················3分(尺规作图得3分)
(2)应用与计算:在(1)的条件下,AD=6,求△BCE的面积.
(2)如图5-19-7,过点B作BF⊥CD于点F.
··················4分(作辅助线得1分)
∵BE为∠ABC的平分线,∴∠ABE=∠CBE.
··················5分(利用角平分线的定义得1分)
∵四边形ABCD为平行四边形,
∴BC=AD=6,AB∥CD,∠C=∠A=60°. ·······6分(利用平行四边形的性质得1分)
∴∠ABE=∠CEB.∴∠CEB=∠CBE.∴CE=BC=6. ············7分(求出CE的长得1分)
温馨提示:此类考题常见于广东省中考数学试卷的第19题,分值一般为9分,答题时要注意书写格式,分步书写,慢做会求全对,评卷老师是分步给分的哦!
【典型错例】论证不严谨
2. 如图5-19-8,在 ABCD中,对角线AC,BD相交于O,OE⊥AD,OF⊥BC,垂足分别是E,F. 求证:OE=OF.
图5-19-8
错解分析
错解:∵四边形ABCD是平行四边形,
∴OD=OB.
∵OE⊥AD,OF⊥BC,∴∠DEO=∠BFO=90°.
又∵∠1=∠2(对顶角相等),
∴△DOE≌△BOF(AAS).∴OE=OF.
剖析:要证明OE=OF,可证明这两条线段所在的三角形全等,那么相对应的两边就相等.错解中默认了E,O,F三点共线,而已知条件中并不能直接得出这个结论,因此E,O,F三点共线在证题过程中必须加以证明,否则就是错误的.
图5-19-8
【生长式训练】知识生长→变式创新
3. (中考创新,原创题)如图5-19-9,BD是 ABCD的一条对角线,过A,C两点分别作AE⊥BD,CF⊥BD,垂足分别为E,F,延长AE,CF分别交CD,AB于点M,N.
知识种子:基本概念
(1)①若AM平分∠BAD,AD=3,AB=7,则CM= ;
②若AD=AM,∠ABC=65°,则∠ADB= ;
图5-19-9
4
40°
种子生长:平行四边形的判定与性质
(2)①求证:四边形CMAN是平行四边形;
①证明:∵AM⊥BD,CN⊥BD,
∴AM∥CN.
∵四边形ABCD是平行四边形,
∴CD∥AB,即CM∥AN.
∴四边形CMAN是平行四边形.
图5-19-9
②若DE=4,FN=3,求BN的长;
图5-19-9
生长变式:图形变式
(3)如图5-19-10,连接AF,CE.
①求证:四边形AECF是平行四边形;
图5-19-10
图5-19-10
种子成树:综合创新
(4)如图5-19-11,BD是四边形ABCD的一条对角线,过A,C两点分别作AM⊥CD,CN⊥AB,垂足分别为M,N,AM,CN分别交BD于点E,F,连接CE,AF.已知四边形AECF是平行四边形,且DE=BF.
①求证:四边形ABCD是平行四边形;
①证明:如答图5-19-1,连接AC交BD于点O.
∵四边形AECF是平行四边形,
∴OA=OC,OE=OF.
∵DE=BF,∴OE+DE=OF+BF,即OD=OB.
∴四边形ABCD是平行四边形.
图5-19-11
答图5-19-1
答图5-19-1
中考演练
(限时15分钟)
一、选择题
1. (2024·贵州)如图5-19-12, ABCD的对角线AC与BD相交于点O,则下列结论一定正确的是 ( )
A. AB=BC
B. AD=BC
C. OA=OB
D. AC⊥BD
图5-19-12
B
2. (2024·巴中)如图5-19-13, ABCD的对角线AC,BD相交于点O,点E是BC的中点,AC=4. 若 ABCD的周长为12,则△COE的周长为( )
A. 4
B. 5
C. 6
D. 8
图5-19-13
B
3. (2024·乐山)如图5-19-14,下列条件不能判定四边形ABCD为平行四边形的是 ( )
A. AB∥DC,AD∥BC
B. AB=DC,AD=BC
C. AO=CO,BO=DO
D. AB∥DC,AD=BC
D
图5-19-14
4. (2024·辽宁)如图5-19-15, ABCD的对角线AC,BD相交于点O,DE∥AC,CE∥BD.若AC=3,BD=5,则四边形OCED的周长为 ( )
A. 4 B. 6
C. 8 D. 16
图5-19-15
C
图5-19-16
B
二、填空题
6. (2024·济宁)如图5-19-17,四边形ABCD的对角线AC,BD相交于点O,OA=OC,请补充一个条件 ,使四边形ABCD是平行四边形.
图5-19-17
OB=OD(答案不唯一)
7. (2024·广州)如图5-19-18, ABCD中,BC=2,点E在DA的延长线上,BE=3.若BA平分∠EBC,则DE= .
图5-19-18
5
8. (2024·广安)如图5-19-19,在 ABCD中,AB=4,AD=5,∠ABC=30°,M为直线BC上一动点,则MA+MD的最小值为 .
图5-19-19
三、解答题
9. (2024·湖北)如图5-19-20,在 ABCD中,E,F是对角线AC上的两点,且AE=CF,求证:BE=DF.
图5-19-20
10. (2024·大庆)如图5-19-21,在 ABCD中,AE,CF分别是∠BAD,∠BCD的平分线,且点E,F分别在边BC,AD上.
(1)求证:四边形AECF是平行四边形;
图5-19-21
(2)若∠ADC=60°,DF=2AF=2,求△GDF的面积.
答图5-19-2
命题趋势
( 限时 5 分钟)
(教材改编)如图5-19-22,在矩形ABCD中,E是AB边的中点,连接CE,将△BCE沿直线CE折叠后,点B落在点B'处,连接AB'并延长交CD于点F.
(1)求证:四边形AECF是平行四边形;
图5-19-22
(1)证明:∵四边形ABCD是矩形,∴AE∥FC.
∵E是AB边的中点,∴AE=BE.
由折叠的性质,得B'E=BE,∠CEB'=∠CEB.
∴AE=B'E.∴∠FAE=∠AB'E.
∵∠BEB'=∠CEB+∠CEB'=∠FAE+∠AB'E,∴2∠CEB=2∠FAE.
∴∠CEB=∠FAE.∴AF∥EC.∴四边形AECF是平行四边形.
(2)若AB=6,BC=4,求tan∠CB'F的值.
图5-19-22
命题解读:根据最新课程标准和近三年中考命题动向,预测2025年中考命题方向可能注重考查平行四边形的基本概念、性质和判定方法,如平行四边形的判定、计算相关角度或边长等;强调与其他几何图形的综合运用,如与三角形、特殊四边形、圆等结合,也可能会与尺规作图相结合;还可能会考查综合探究类题型,通过变换图形位置或构造特殊图形综合考查.
第五章 四 边 形
第19课时 平行四边形
课前循环练
(限时5分钟)
C
C
3. (广东真题)如图5-19-1,在菱形ABCD中,∠ADB与∠ABD的大小关系是 ( )
A.∠ADB>∠ABD
B.∠ADB<∠ABD
C.∠ADB=∠ABD
D. 无法确定
图5-19-1
C
4. (广东真题)命题“平行四边形的对角线互相平分”的逆命题是_______
.
5. (广东真题)如图5-19-2,PA,PB是☉O的切线,点A,B为切点,AC是☉O的直径,∠BAC=20°,则∠P的大小是 .
对角线互相平分的四边形是平行四边形
40°
图5-19-2
①理解平行四边形的概念.
②探索并证明平行四边形的性质定理:平行四边形的对边相等、对角相等、对角线互相平分. 探索并证明平行四边形的判定定理:一组对边平行且相等的四边形是平行四边形;两组对边分别相等的四边形是平行四边形;对角线互相平分的四边形是平行四边形.
③理解两条平行线之间距离的概念,能度量两条平行线之间的距离.
课标要求
对接教材 人教:八下第十八章 平行四边形
北师:八下第六章 平行四边形
考点梳理
考点复习
1.平行四边形的概念
两组对边分别 的四边形叫做平行四边形
平行
广东省对应考点例题
例1. 在 ABCD中,∠A=100°,则∠B= .
80°
2.平行四边形的性质与判定
性质 判定
边 平行四边形的对边 (1)两组对边分别 的四边形是平行四边形;
(2)两组对边分别 的四边形是平行四边形;
(3)一组对边 的四边形是平行四边形
角 平行四边形的对角 两组对角 的四边形是平行四边形
对角
线 平行四边形的对角线_______
对角线 的四边形是平行四边形
对称性 平行四边形是中心对称图形,它的对称中心是
平行且相等
平行
相等
平行且相等
相等
相等
互相
平分
互相平分
对角线的交点
例2. 如图5-19-3,在 ABCD中,对角线AC,BD相交于点O,E,F是对角线AC上的两点,当点E,F满足下列哪个条件时,四边形DEBF不一定是平行四边形? ( )
A. OE=OF
B. DF=BE
C. AE=CF
D.∠AEB=∠CFD
图5-19-3
B
3.平行四边形的面积
(1)平行四边形的面积= .
(2)同底(等底)同高(等高)的平行四边形的面积 .
(3)如果两条直线相互平行,那么其中一条直线上任意一点到另一条直线的距离都相等,这个距离称为平行线之间的距离.平行线间的距离处处
底×高
相等
相等
例3. 如图5-19-4, ABCD的对角线AC与BD相交于点O,过点O的直线分别交CD和AB于点E,F,且AB=7,BC=4,∠BCD=30°,则 ABCD的面积为 ,图中阴影部分的面积为 .
图5-19-4
14
7
广东中考
(2022·广东题8,3分,平行四边形的性质)如图5-19-5,在 ABCD中,一定正确的是 ( )
A. AD=CD
B. AC=BD
C. AB=CD
D. CD=BC
图5-19-5
C
高分击破
【典型考点】尺规作图;角平分线的性质;平行四边形的性质 得分点分析
1.如图5-19-6,在 ABCD中,∠A=60°.
(1)实践与操作:用尺规作图法过点B作∠ABC的平分线,交边CD于点E;(保留作图痕迹,不要求写作法)
解:(1)如图5-19-7,BE即为所作. ······················3分(尺规作图得3分)
(2)应用与计算:在(1)的条件下,AD=6,求△BCE的面积.
(2)如图5-19-7,过点B作BF⊥CD于点F.
··················4分(作辅助线得1分)
∵BE为∠ABC的平分线,∴∠ABE=∠CBE.
··················5分(利用角平分线的定义得1分)
∵四边形ABCD为平行四边形,
∴BC=AD=6,AB∥CD,∠C=∠A=60°. ·······6分(利用平行四边形的性质得1分)
∴∠ABE=∠CEB.∴∠CEB=∠CBE.∴CE=BC=6. ············7分(求出CE的长得1分)
温馨提示:此类考题常见于广东省中考数学试卷的第19题,分值一般为9分,答题时要注意书写格式,分步书写,慢做会求全对,评卷老师是分步给分的哦!
【典型错例】论证不严谨
2. 如图5-19-8,在 ABCD中,对角线AC,BD相交于O,OE⊥AD,OF⊥BC,垂足分别是E,F. 求证:OE=OF.
图5-19-8
错解分析
错解:∵四边形ABCD是平行四边形,
∴OD=OB.
∵OE⊥AD,OF⊥BC,∴∠DEO=∠BFO=90°.
又∵∠1=∠2(对顶角相等),
∴△DOE≌△BOF(AAS).∴OE=OF.
剖析:要证明OE=OF,可证明这两条线段所在的三角形全等,那么相对应的两边就相等.错解中默认了E,O,F三点共线,而已知条件中并不能直接得出这个结论,因此E,O,F三点共线在证题过程中必须加以证明,否则就是错误的.
图5-19-8
【生长式训练】知识生长→变式创新
3. (中考创新,原创题)如图5-19-9,BD是 ABCD的一条对角线,过A,C两点分别作AE⊥BD,CF⊥BD,垂足分别为E,F,延长AE,CF分别交CD,AB于点M,N.
知识种子:基本概念
(1)①若AM平分∠BAD,AD=3,AB=7,则CM= ;
②若AD=AM,∠ABC=65°,则∠ADB= ;
图5-19-9
4
40°
种子生长:平行四边形的判定与性质
(2)①求证:四边形CMAN是平行四边形;
①证明:∵AM⊥BD,CN⊥BD,
∴AM∥CN.
∵四边形ABCD是平行四边形,
∴CD∥AB,即CM∥AN.
∴四边形CMAN是平行四边形.
图5-19-9
②若DE=4,FN=3,求BN的长;
图5-19-9
生长变式:图形变式
(3)如图5-19-10,连接AF,CE.
①求证:四边形AECF是平行四边形;
图5-19-10
图5-19-10
种子成树:综合创新
(4)如图5-19-11,BD是四边形ABCD的一条对角线,过A,C两点分别作AM⊥CD,CN⊥AB,垂足分别为M,N,AM,CN分别交BD于点E,F,连接CE,AF.已知四边形AECF是平行四边形,且DE=BF.
①求证:四边形ABCD是平行四边形;
①证明:如答图5-19-1,连接AC交BD于点O.
∵四边形AECF是平行四边形,
∴OA=OC,OE=OF.
∵DE=BF,∴OE+DE=OF+BF,即OD=OB.
∴四边形ABCD是平行四边形.
图5-19-11
答图5-19-1
答图5-19-1
中考演练
(限时15分钟)
一、选择题
1. (2024·贵州)如图5-19-12, ABCD的对角线AC与BD相交于点O,则下列结论一定正确的是 ( )
A. AB=BC
B. AD=BC
C. OA=OB
D. AC⊥BD
图5-19-12
B
2. (2024·巴中)如图5-19-13, ABCD的对角线AC,BD相交于点O,点E是BC的中点,AC=4. 若 ABCD的周长为12,则△COE的周长为( )
A. 4
B. 5
C. 6
D. 8
图5-19-13
B
3. (2024·乐山)如图5-19-14,下列条件不能判定四边形ABCD为平行四边形的是 ( )
A. AB∥DC,AD∥BC
B. AB=DC,AD=BC
C. AO=CO,BO=DO
D. AB∥DC,AD=BC
D
图5-19-14
4. (2024·辽宁)如图5-19-15, ABCD的对角线AC,BD相交于点O,DE∥AC,CE∥BD.若AC=3,BD=5,则四边形OCED的周长为 ( )
A. 4 B. 6
C. 8 D. 16
图5-19-15
C
图5-19-16
B
二、填空题
6. (2024·济宁)如图5-19-17,四边形ABCD的对角线AC,BD相交于点O,OA=OC,请补充一个条件 ,使四边形ABCD是平行四边形.
图5-19-17
OB=OD(答案不唯一)
7. (2024·广州)如图5-19-18, ABCD中,BC=2,点E在DA的延长线上,BE=3.若BA平分∠EBC,则DE= .
图5-19-18
5
8. (2024·广安)如图5-19-19,在 ABCD中,AB=4,AD=5,∠ABC=30°,M为直线BC上一动点,则MA+MD的最小值为 .
图5-19-19
三、解答题
9. (2024·湖北)如图5-19-20,在 ABCD中,E,F是对角线AC上的两点,且AE=CF,求证:BE=DF.
图5-19-20
10. (2024·大庆)如图5-19-21,在 ABCD中,AE,CF分别是∠BAD,∠BCD的平分线,且点E,F分别在边BC,AD上.
(1)求证:四边形AECF是平行四边形;
图5-19-21
(2)若∠ADC=60°,DF=2AF=2,求△GDF的面积.
答图5-19-2
命题趋势
( 限时 5 分钟)
(教材改编)如图5-19-22,在矩形ABCD中,E是AB边的中点,连接CE,将△BCE沿直线CE折叠后,点B落在点B'处,连接AB'并延长交CD于点F.
(1)求证:四边形AECF是平行四边形;
图5-19-22
(1)证明:∵四边形ABCD是矩形,∴AE∥FC.
∵E是AB边的中点,∴AE=BE.
由折叠的性质,得B'E=BE,∠CEB'=∠CEB.
∴AE=B'E.∴∠FAE=∠AB'E.
∵∠BEB'=∠CEB+∠CEB'=∠FAE+∠AB'E,∴2∠CEB=2∠FAE.
∴∠CEB=∠FAE.∴AF∥EC.∴四边形AECF是平行四边形.
(2)若AB=6,BC=4,求tan∠CB'F的值.
图5-19-22
命题解读:根据最新课程标准和近三年中考命题动向,预测2025年中考命题方向可能注重考查平行四边形的基本概念、性质和判定方法,如平行四边形的判定、计算相关角度或边长等;强调与其他几何图形的综合运用,如与三角形、特殊四边形、圆等结合,也可能会与尺规作图相结合;还可能会考查综合探究类题型,通过变换图形位置或构造特殊图形综合考查.
同课章节目录
