中考数学复习知识梳理第六章圆第23课时与圆有关的计算课件(共46张PPT)
文档属性
| 名称 | 中考数学复习知识梳理第六章圆第23课时与圆有关的计算课件(共46张PPT) |  | |
| 格式 | ppt | ||
| 文件大小 | 8.8MB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 通用版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2025-05-31 09:38:37 | ||
图片预览









文档简介
(共46张PPT)
第六章 圆
第23课时 与圆有关的计算
课前循环练
(限时5分钟)
D
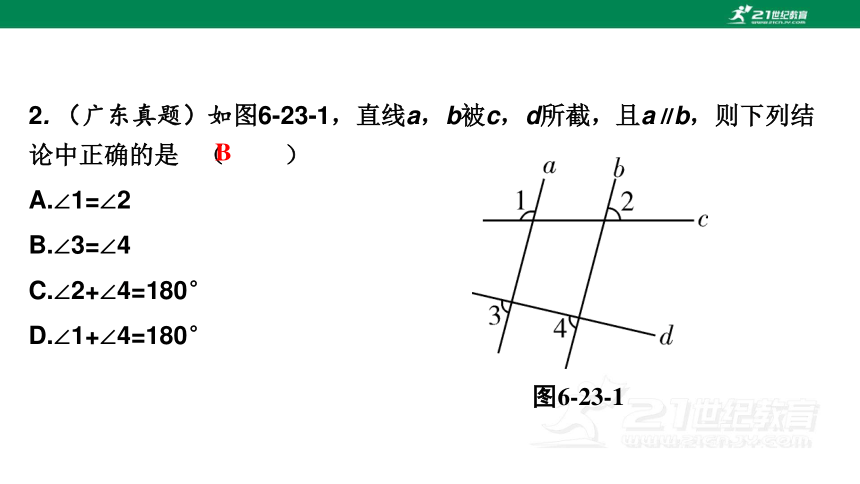
2. (广东真题)如图6-23-1,直线a,b被c,d所截,且a∥b,则下列结论中正确的是 ( )
A.∠1=∠2
B.∠3=∠4
C.∠2+∠4=180°
D.∠1+∠4=180°
图6-23-1
B
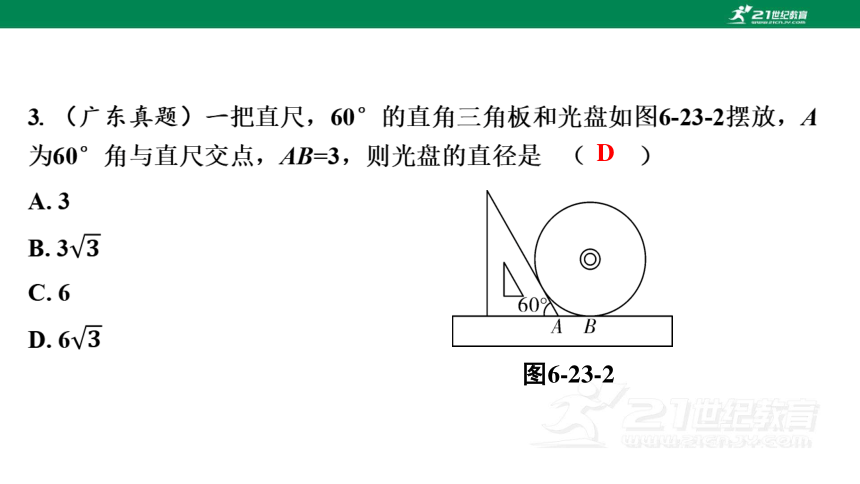
图6-23-2
D
4. (广东真题)如图6-23-3,两个同心圆的半径分别为2和1,∠AOB=120°,则阴影部分的面积为 .
图6-23-3
π
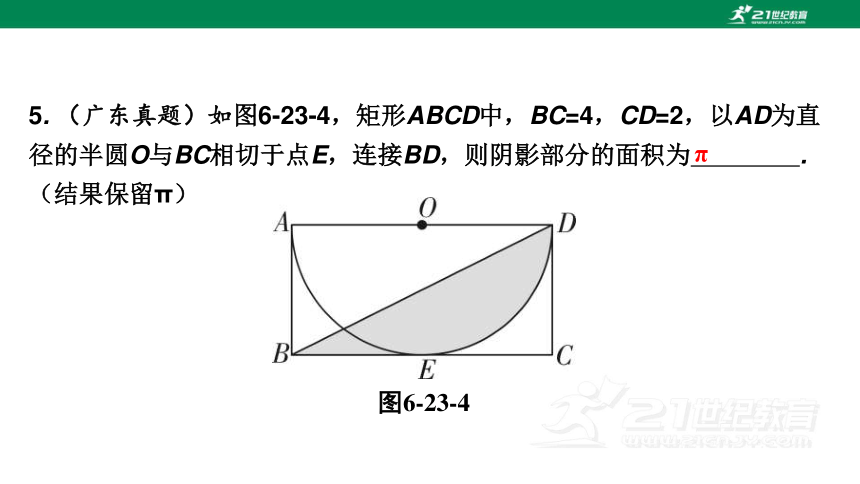
5. (广东真题)如图6-23-4,矩形ABCD中,BC=4,CD=2,以AD为直径的半圆O与BC相切于点E,连接BD,则阴影部分的面积为 .(结果保留π)
图6-23-4
π
①会计算圆的弧长、扇形的面积.
②了解正多边形的概念及正多边形与圆的关系.
课标要求
对接教材 人教:九上第二十四章 圆
北师:九下第三章 圆
考点梳理
考点复习
1.弧长的计算公式
在半径为R的圆中,n°的圆心角所对的弧长的计算公式为l=
广东省对应考点例题
例1. 已知扇形的半径是30 cm,圆心角是60°,则该扇形弧长为 cm.
10π
2.扇形面积的计算公式
(1)如果扇形的半径为R,圆心角为n°,那么扇形面积的计算公式为
S扇形= ;
(2)比较扇形面积公式与弧长公式,用弧长来表示扇形的面积:S扇形=
例2. (1)(2023·新疆)如图6-23-5,在☉O中,若∠ACB=30°,OA=6,则扇形OAB(阴影部分)的面积是 ( )
A. 12π B. 6π
C. 4π D. 2π
(2)一个扇形的半径是6 cm,弧长是5π cm,则此扇形的面积是
cm2.
图6-23-5
B
15π
图6-23-6
底面周长
母线长
πrl
πr2+πrl
15π
24π
12π
D
4.正多边形和圆
(1)正多边形:各边相等、各角也相等的多边形叫做正多边形.
(2)正多边形的中心:正多边形外接圆的 叫做正多边形的中心.
(3)正多边形的半径:正多边形外接圆的 叫做正多边形的半径.
(4)正多边形的中心角:正多边形的每条边所对的 叫做正多边形的中心角.
(5)正多边形的边心距:中心到正多边形的一边的 叫做正多边形的边心距
圆心
半径
圆心角
距离
例4. 如图6-23-7,已知☉O的半径R=6 cm,则☉O的内接正六边形ABCDEF的边心距是 ,中心角是 ,边长是 ,周长是 ,面积是 .
图6-23-7
60°
6 cm
36 cm
广东中考
1. (2022·广东题15,3分,扇形面积的计算)扇形的半径为2,圆心角为90°,则该扇形的面积为 . (结果保留π)
π
2. (2021·广东题13,4分,等腰直角三角形;扇形面积的计算)如图6-23-8,等腰直角三角形ABC中,∠A=90°,BC=4. 分别以点B,点C为圆心,线段BC长的一半为半径作圆弧,交AB,BC,AC于点D,E,F,则图中阴影部分的面积为 .
图6-23-8
4-π
3. (2020·广东题16,4分,弧长的计算;圆锥的计算)如图6-23-9,从一块半径为1 m的圆形铁皮上剪出一个圆周角为120°的扇形ABC,如果将剪下来的扇形围成一个圆锥,那么该圆锥的底面圆的半径为 m.
图6-23-9
高分击破
【典型考点】圆锥的计算;展开图折叠成几何体;综合与实践
得分点分析
1. (教材改编)图6-23-10①中的某种冰激凌的外包装可以视为圆锥(如图6-23-10②),制作这种外包装需要用如图6-23-10③所示的等腰三角形材料,其中AB=AC,AD⊥BC,将扇形EAF围成圆锥时,AE,AF恰好重合,已知这种加工材料的顶角∠BAC=90°.
····································································
(1)求图6-23-10②中圆锥底面圆直径ED与母线AD长的比值;
图6-23-10
(2)若圆锥底面圆的直径ED为5 cm,求加工材料剩余部分(图6-23-10③中阴影部分)的面积.(结果保留π)
图6-23-10
温馨提示:此类考题常见于广东省中考数学试卷的第21小题,分值一般为9分,答题时要注意书写格式,分步书写,慢做会求全对,评卷老师是分步给分的哦!
【典型错例】不能正确使用分割法求面积
2. 如图6-23-11,大正方形ABCD的边长为4,小正方形ECGF的边长为2,扇形BCD和扇形EFG的圆心分别为点C和点F,半径分别为4和2,点E,点G分别在边BC和CD上.
(1)求阴影部分的面积;
图6-23-11
(2)求阴影部分的周长.
图6-23-11
图6-23-11
图6-23-12
4π
12π
种子生长:圆锥的计算
(2)如图6-23-13,将此扇形围成一个圆锥.
①求围成圆锥的底面半径r和高h;
图6-23-13
②求围成圆锥的全面积和体积;
图6-23-13
生长变式:图形变式
(3)如图6-23-14,C是OA上的一点,连接BC.若OC=4,求阴影部分的面积;
图6-23-14
答图6-23-1
图6-23-15
答图6-23-2
如答图6-23-2②,连接ON,则ON⊥JM.
∴ON=JK=OA=OB=6.
在Rt△AOK中,∠AOK=60°,
∴OK=OA·cos∠AOK=6×cos 60°=3.
∴KL=OK+OL=OK+OB=9.
∴矩形铁皮JKLM的面积为JK·KL=6×9=54.
∵61.2>54,∴矩形铁皮EFGH的面积较大.
答图6-23-2
中考演练
(限时15分钟)
图6-23-16
C
图6-23-17
D
图6-23-18
B
图6-23-19
D
图6-23-20
D
图6-23-21
4π
图6-23-22
90
三、解答题
9. (2024·青海)如图6-23-23,直线AB经过点C,且OA=OB,CA=CB.
(1)求证:直线AB是☉O的切线;
图6-23-23
(1)证明:如答图6-23-3,连接OC.
∵直线AB经过点C,∴OC是☉O的半径.
∵OA=OB,CA=CB,∴OC⊥AB.∴直线AB是☉O的切线.
(2)若圆的半径为4,∠B=30°,求阴影部分的面积.
图6-23-23
答图6-23-3
10. (2024·齐齐哈尔)如图6-23-24,△ABC内接于☉O,AB为☉O的直径,CD⊥AB于点D,将△CDB沿BC所在的直线翻折,得到△CEB,点D的对应点为E,延长EC交BA的延长线于点F.
图6-23-24
(1)求证:CF是☉O的切线;
(1)证明:如答图6-23-4,连接OC.
∵CD⊥AB,∴∠BDC=90°.
由翻折的性质,得∠EBC=∠DBC,
∠E=∠BDC=90°.
∵OC=OB,∴∠OCB=∠DBC.∴∠OCB=∠EBC.∴OC∥BE.
∴∠OCF=∠E=90°,即OC⊥CF.
又∵OC是☉O的半径,∴CF是☉O的切线.
答图6-23-4
答图6-23-4
命题趋势
( 限时 5 分钟)
(教材改编)综合与实践
主题:制作圆锥形生日帽.
素材:一张圆形纸板、装饰彩带.
步骤1:如图6-23-25①,将一个底面半径为r的圆锥
侧面展开,可得到一个半径为l、圆心角为n°的扇
形. 制作圆锥形生日帽时,要先确定扇形的圆心角
度数,再度量裁剪材料.
步骤2:如图6-23-25②,把剪好的纸板粘合成圆锥形生日帽.
图6-23-25
(1)现在需要制作一个r=10 cm,l=30 cm的生日帽,请帮忙计算出所需扇形纸板的圆心角度数;
图6-23-25
(2)为了使(1)中所制作的生日帽更美观,要粘贴彩带进行装饰,其中需要粘贴一条从点A处开始,绕侧面一周又回到点A的彩带(彩带宽度忽略不计),求彩带长度的最小值.
答图6-23-5
命题解读:根据最新课程标准和近三年中考命题动向,预测2025年中考命题方向可能注重考查扇形、弓形、圆锥等与圆相关的图形的面积、弧长、半径等计算;强调与三角形、四边形等其他几何图形的综合运用,可能涉及阴影部分面积的计算;还可能会考查创新题型,如实际情境问题、综合与实践问题等.
第六章 圆
第23课时 与圆有关的计算
课前循环练
(限时5分钟)
D
2. (广东真题)如图6-23-1,直线a,b被c,d所截,且a∥b,则下列结论中正确的是 ( )
A.∠1=∠2
B.∠3=∠4
C.∠2+∠4=180°
D.∠1+∠4=180°
图6-23-1
B
图6-23-2
D
4. (广东真题)如图6-23-3,两个同心圆的半径分别为2和1,∠AOB=120°,则阴影部分的面积为 .
图6-23-3
π
5. (广东真题)如图6-23-4,矩形ABCD中,BC=4,CD=2,以AD为直径的半圆O与BC相切于点E,连接BD,则阴影部分的面积为 .(结果保留π)
图6-23-4
π
①会计算圆的弧长、扇形的面积.
②了解正多边形的概念及正多边形与圆的关系.
课标要求
对接教材 人教:九上第二十四章 圆
北师:九下第三章 圆
考点梳理
考点复习
1.弧长的计算公式
在半径为R的圆中,n°的圆心角所对的弧长的计算公式为l=
广东省对应考点例题
例1. 已知扇形的半径是30 cm,圆心角是60°,则该扇形弧长为 cm.
10π
2.扇形面积的计算公式
(1)如果扇形的半径为R,圆心角为n°,那么扇形面积的计算公式为
S扇形= ;
(2)比较扇形面积公式与弧长公式,用弧长来表示扇形的面积:S扇形=
例2. (1)(2023·新疆)如图6-23-5,在☉O中,若∠ACB=30°,OA=6,则扇形OAB(阴影部分)的面积是 ( )
A. 12π B. 6π
C. 4π D. 2π
(2)一个扇形的半径是6 cm,弧长是5π cm,则此扇形的面积是
cm2.
图6-23-5
B
15π
图6-23-6
底面周长
母线长
πrl
πr2+πrl
15π
24π
12π
D
4.正多边形和圆
(1)正多边形:各边相等、各角也相等的多边形叫做正多边形.
(2)正多边形的中心:正多边形外接圆的 叫做正多边形的中心.
(3)正多边形的半径:正多边形外接圆的 叫做正多边形的半径.
(4)正多边形的中心角:正多边形的每条边所对的 叫做正多边形的中心角.
(5)正多边形的边心距:中心到正多边形的一边的 叫做正多边形的边心距
圆心
半径
圆心角
距离
例4. 如图6-23-7,已知☉O的半径R=6 cm,则☉O的内接正六边形ABCDEF的边心距是 ,中心角是 ,边长是 ,周长是 ,面积是 .
图6-23-7
60°
6 cm
36 cm
广东中考
1. (2022·广东题15,3分,扇形面积的计算)扇形的半径为2,圆心角为90°,则该扇形的面积为 . (结果保留π)
π
2. (2021·广东题13,4分,等腰直角三角形;扇形面积的计算)如图6-23-8,等腰直角三角形ABC中,∠A=90°,BC=4. 分别以点B,点C为圆心,线段BC长的一半为半径作圆弧,交AB,BC,AC于点D,E,F,则图中阴影部分的面积为 .
图6-23-8
4-π
3. (2020·广东题16,4分,弧长的计算;圆锥的计算)如图6-23-9,从一块半径为1 m的圆形铁皮上剪出一个圆周角为120°的扇形ABC,如果将剪下来的扇形围成一个圆锥,那么该圆锥的底面圆的半径为 m.
图6-23-9
高分击破
【典型考点】圆锥的计算;展开图折叠成几何体;综合与实践
得分点分析
1. (教材改编)图6-23-10①中的某种冰激凌的外包装可以视为圆锥(如图6-23-10②),制作这种外包装需要用如图6-23-10③所示的等腰三角形材料,其中AB=AC,AD⊥BC,将扇形EAF围成圆锥时,AE,AF恰好重合,已知这种加工材料的顶角∠BAC=90°.
····································································
(1)求图6-23-10②中圆锥底面圆直径ED与母线AD长的比值;
图6-23-10
(2)若圆锥底面圆的直径ED为5 cm,求加工材料剩余部分(图6-23-10③中阴影部分)的面积.(结果保留π)
图6-23-10
温馨提示:此类考题常见于广东省中考数学试卷的第21小题,分值一般为9分,答题时要注意书写格式,分步书写,慢做会求全对,评卷老师是分步给分的哦!
【典型错例】不能正确使用分割法求面积
2. 如图6-23-11,大正方形ABCD的边长为4,小正方形ECGF的边长为2,扇形BCD和扇形EFG的圆心分别为点C和点F,半径分别为4和2,点E,点G分别在边BC和CD上.
(1)求阴影部分的面积;
图6-23-11
(2)求阴影部分的周长.
图6-23-11
图6-23-11
图6-23-12
4π
12π
种子生长:圆锥的计算
(2)如图6-23-13,将此扇形围成一个圆锥.
①求围成圆锥的底面半径r和高h;
图6-23-13
②求围成圆锥的全面积和体积;
图6-23-13
生长变式:图形变式
(3)如图6-23-14,C是OA上的一点,连接BC.若OC=4,求阴影部分的面积;
图6-23-14
答图6-23-1
图6-23-15
答图6-23-2
如答图6-23-2②,连接ON,则ON⊥JM.
∴ON=JK=OA=OB=6.
在Rt△AOK中,∠AOK=60°,
∴OK=OA·cos∠AOK=6×cos 60°=3.
∴KL=OK+OL=OK+OB=9.
∴矩形铁皮JKLM的面积为JK·KL=6×9=54.
∵61.2>54,∴矩形铁皮EFGH的面积较大.
答图6-23-2
中考演练
(限时15分钟)
图6-23-16
C
图6-23-17
D
图6-23-18
B
图6-23-19
D
图6-23-20
D
图6-23-21
4π
图6-23-22
90
三、解答题
9. (2024·青海)如图6-23-23,直线AB经过点C,且OA=OB,CA=CB.
(1)求证:直线AB是☉O的切线;
图6-23-23
(1)证明:如答图6-23-3,连接OC.
∵直线AB经过点C,∴OC是☉O的半径.
∵OA=OB,CA=CB,∴OC⊥AB.∴直线AB是☉O的切线.
(2)若圆的半径为4,∠B=30°,求阴影部分的面积.
图6-23-23
答图6-23-3
10. (2024·齐齐哈尔)如图6-23-24,△ABC内接于☉O,AB为☉O的直径,CD⊥AB于点D,将△CDB沿BC所在的直线翻折,得到△CEB,点D的对应点为E,延长EC交BA的延长线于点F.
图6-23-24
(1)求证:CF是☉O的切线;
(1)证明:如答图6-23-4,连接OC.
∵CD⊥AB,∴∠BDC=90°.
由翻折的性质,得∠EBC=∠DBC,
∠E=∠BDC=90°.
∵OC=OB,∴∠OCB=∠DBC.∴∠OCB=∠EBC.∴OC∥BE.
∴∠OCF=∠E=90°,即OC⊥CF.
又∵OC是☉O的半径,∴CF是☉O的切线.
答图6-23-4
答图6-23-4
命题趋势
( 限时 5 分钟)
(教材改编)综合与实践
主题:制作圆锥形生日帽.
素材:一张圆形纸板、装饰彩带.
步骤1:如图6-23-25①,将一个底面半径为r的圆锥
侧面展开,可得到一个半径为l、圆心角为n°的扇
形. 制作圆锥形生日帽时,要先确定扇形的圆心角
度数,再度量裁剪材料.
步骤2:如图6-23-25②,把剪好的纸板粘合成圆锥形生日帽.
图6-23-25
(1)现在需要制作一个r=10 cm,l=30 cm的生日帽,请帮忙计算出所需扇形纸板的圆心角度数;
图6-23-25
(2)为了使(1)中所制作的生日帽更美观,要粘贴彩带进行装饰,其中需要粘贴一条从点A处开始,绕侧面一周又回到点A的彩带(彩带宽度忽略不计),求彩带长度的最小值.
答图6-23-5
命题解读:根据最新课程标准和近三年中考命题动向,预测2025年中考命题方向可能注重考查扇形、弓形、圆锥等与圆相关的图形的面积、弧长、半径等计算;强调与三角形、四边形等其他几何图形的综合运用,可能涉及阴影部分面积的计算;还可能会考查创新题型,如实际情境问题、综合与实践问题等.
同课章节目录
