中考数学复习知识梳理第六章圆第21课时圆的有关概念及性质课件(共52张PPT)
文档属性
| 名称 | 中考数学复习知识梳理第六章圆第21课时圆的有关概念及性质课件(共52张PPT) |  | |
| 格式 | ppt | ||
| 文件大小 | 6.7MB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 通用版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2025-05-31 09:46:04 | ||
图片预览









文档简介
(共52张PPT)
第六章 圆
第21课时 圆的有关概念及性质
课前循环练
(限时5分钟)
A
D
C
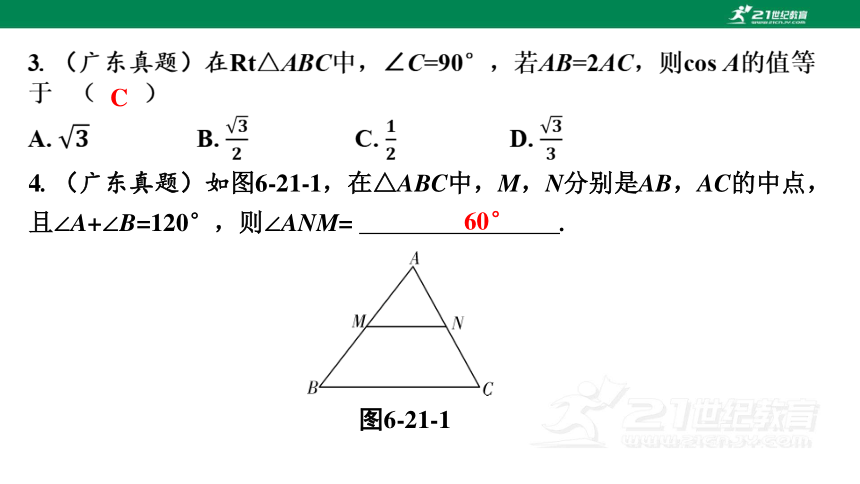
4. (广东真题)如图6-21-1,在△ABC中,M,N分别是AB,AC的中点,且∠A+∠B=120°,则∠ANM= .
图6-21-1
60°
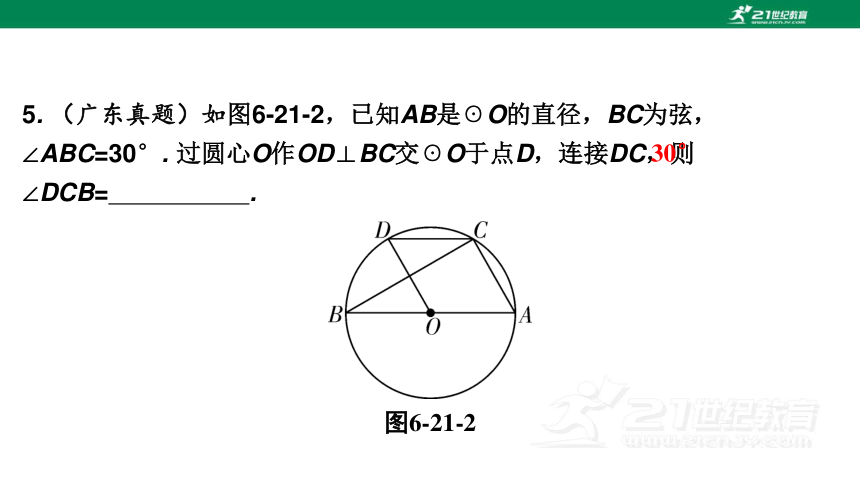
5. (广东真题)如图6-21-2,已知AB是☉O的直径,BC为弦,∠ABC=30°. 过圆心O作OD⊥BC交☉O于点D,连接DC,则∠DCB= .
图6-21-2
30°
①理解圆、弧、弦、圆心角、圆周角的概念,了解等圆、等弧的概念.
②探索并证明垂径定理:垂直于弦的直径平分弦以及弦所对的两条弧.
③探索圆周角与圆心角及其所对弧的关系,知道同弧(或等弧)所对的圆周角相等. 了解并证明圆周角定理及其推论:圆周角等于它所对弧上的圆心角的一半;直径所对的圆周角是直角,90°的圆周角所对的弦是直径;圆内接四边形的对角互补.
课标要求
对接教材 人教:九上第二十四章 圆
北师:九下第三章 圆
考点梳理
考点复习
1.圆
平面上到定点的距离等于定长的所有点组成的图形叫做圆.其中,定点称为 ,定长称为
圆心
半径
广东省对应考点例题
例1. 下列条件中,能确定一个圆的是 ( )
A.以点O为圆心
B.以2 cm长为半径
C.以点O为圆心,5 cm长为半径
D.经过点A
C
2.圆的对称性
(1)圆是轴对称图形,其对称轴是任意一条 的直线,有
条对称轴.
(2)圆是中心对称图形,对称中心为
过圆心
无数
圆心
例2. 下列说法中,不正确的是 ( )
A.圆是轴对称图形,有无数条对称轴
B.圆是中心对称图形,有无数个对称中心
C. 圆的任意一条直径所在直线都是圆的对称轴
D.圆既是轴对称图形,又是中心对称图形
B
3.与圆有关的概念
(1)弧:圆上任意 的部分叫做圆弧,简称弧.
(2)弦:连接圆上任意两点的 叫做弦.
(3)直径:经过 的弦叫做直径.
(4)圆心角:顶点在 的角叫做圆心角.
(5)圆周角:顶点在 ,两边分别与圆还有另一个交点.像这样的角,叫做圆周角
两点间
线段
圆心
圆心
圆上
例3. 下列命题:①圆上任意两点间的部分叫弧;②圆心角相等则它们所对的弧相等;③在同一个圆中,直径是最长的弦;④直径是圆的对称轴;⑤顶点在圆上的角是圆周角;⑥顶点在圆心的角是圆心角.
其中正确的有 ( )
A. ①③⑤ B. ②④⑥
C. ①③⑥ D. ②③⑤
C
4.圆心角、弧、弦之间的关系
(1)在同圆或等圆中,相等的圆心角所对的弧 ,所对的弦
.
(2)在同圆或等圆中,如果两个圆心角、两条弧、两条弦中有一组量相等,那么它们所对应的其余各组量都分别
相等
相等
相等
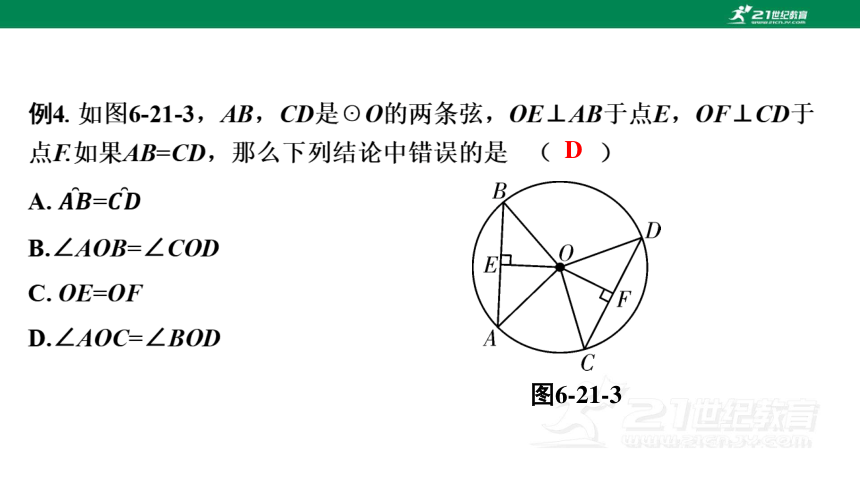
图6-21-3
D
5.垂径定理及其推论
(1)垂径定理:垂直于弦的直径 这条弦,并且 弦所对的弧.
(2)推论:①平分弦(不是直径)的直径 于弦,并且 弦所对的弧;
②弦的垂直平分线经过 ,并且平分弦所对的两条弧;
③平分弦所对的一条弧的直径 弦,并且 弦所对的另一条弧
平分
平分
垂直
平分
圆心
垂直平分
平分
图6-21-4
B
6.圆周角定理及其推论
(1)圆周角定理:圆周角的度数等于它所对弧上的圆心角度数的______
.
(2)推论:①同弧或等弧所对的圆周角 ;
②半圆(或直径)所对的圆周角是 ,90°的圆周角所对的弦是 ;
③圆内接四边形的对角
一半
相等
直角
直径
互补
例6. 如图6-21-5,四边形ABCD内接于☉O,E为DC延长线上一点,BF为☉O的直径,连接DF,DB,∠FBD=40°,则∠BCE的度数为 ( )
A. 40°
B. 50°
C. 60°
D. 130°
图6-21-5
B
广东中考
1. (2023·广东题9,3分,圆周角定理的推论)如图6-21-6,AB是☉O的直径,∠BAC=50°,则∠D= ( )
A. 20° B. 40°
C. 50° D. 80°
图6-21-6
B
图6-21-7
B
3. (2022·广东题22,12分,圆周角定理的推论;等腰直角三角形;勾股定理)如图6-21-8,四边形ABCD内接于☉O,AC为☉O的直径,∠ADB=∠CDB.
(1)试判断△ABC的形状,并给出证明;
图6-21-8
图6-21-8
高分击破
【典型考点】圆内接四边形的性质;翻折变换(折叠问题);圆周角定理
得分点分析
1. (2022·广东改编,综合探究)如图6-21-9①,已知四边形ABCD内接于☉O,AC为☉O的直径,∠BAC=∠ADB.
····································································
图6-21-9
(1)试说明△ABC的形状;
解:(1)∵AC为☉O的直径,
∴∠ABC=90°.
··············1分(利用“直径所对的圆周角是直角”得1分)
∵∠ADB=∠ACB,∠BAC=∠ADB,
··············2分(利用“同弧所对的圆周角相等”得1分)
∴∠BAC=∠ACB.∴AB=BC. ··················3分(利用等量代换,等角对等边得1分)
∴△ABC是等腰直角三角形. ··············4分(利用等腰直角三角形的判定得1分)
图6-21-9
图6-21-9
②将△ABD沿BD所在的直线折叠(如图6-21-9②),得到△A'BD,连接A'C,求∠BA'C的度数.
图6-21-9
∴折叠后,点A的对应点A'恰好落在DC上. ·······10分(确定点A'的位置得1分)
∵∠BAD=∠BAC+∠DAC=45°+60°=105°, ····························11分(求出∠BAD的度数得1分)
∴∠BA'D=∠BAD=105°. ···································12分(利用折叠的性质得1分)
∴∠BA'C=180°-∠BA'D=180°-105°=75°. ····························13分(求出∠BA'C的度数得1分)
图6-21-9
温馨提示:此类考题常见于广东省中考数学试卷的第22题,分值一般为13分,答题时要注意书写格式,分步书写,慢做会求全对,评卷老师是分步给分的哦!
【典型错例】无图题考察圆周角的应用时没有分类讨论导致漏解
2. 已知☉O是△ABC的外接圆,过顶点A,B分别作☉O的切线,它们交于点P,若∠APB=50°,求∠ACB的度数.
答图6-21-1
图6-21-10
图6-21-11
60°
120°
<
种子生长:垂径定理
(2)若AE=CD,BE=2,求☉O的半径;
答图6-21-2
生长变式:图形变式
(3)如图6-21-12,在(2)的条件下,延长AG,DC交于点F,连接DG.若G是AF的中点,求AG的长;
图6-21-12
解:如答图6-21-3,连接BG.
∵AB是☉O的直径,∴∠AGB=90°.∴∠B+∠BAG=90°.
∵AB⊥CD,∴∠AEF=90°.∴∠F+∠BAG=90°.
∴∠B=∠F.
∵∠ADG=∠B,∴∠ADG=∠F.
又∵∠DAG=∠FAD,∴△ADG∽△AFD.
答图6-21-3
答图6-21-3
答图6-21-4
答图6-21-4
答图6-21-5
中考演练
(限时15分钟)
一、选择题
1. (2024·湖南)如图6-21-13,AB,AC为☉O的两条弦,连接OB,OC.若∠A=45°,则∠BOC的度数为 ( )
A. 60° B. 75°
C. 90° D. 135°
图6-21-13
C
图6-21-14
B
图6-21-15
C
4. (2024·广元)如图6-21-16,已知四边形ABCD是☉O的内接四边形,E为AD延长线上一点,∠AOC=128°,则∠CDE等于 ( )
A. 64°
B. 60°
C. 54°
D. 52°
图6-21-16
A
5. (2024·通辽)如图6-21-17,圆形拱门最下端AB在地面上,D为AB的中点,C为拱门最高点,线段CD经过拱门所在圆的圆心.若AB=1 m,CD=2.5 m,则拱门所在圆的半径为 ( )
A. 1.25 m B. 1.3 m
C. 1.4 m D. 1.45 m
图6-21-17
B
二、填空题
6. (2024·苏州)如图6-21-18,△ABC是☉O的内接三角形,若∠OBC=28°,则∠A= °.
图6-21-18
62
7. (2024·巴中)如图6-21-19,四边形ABCD为☉O的内接四边形. 若四边形ABCO为菱形,则∠ADC的大小为 .
图6-21-19
60°
8. (2024·牡丹江)如图6-21-20,在☉O中,直径AB⊥CD于点E,CD=6,BE=1,则弦AC的长为 .
图6-21-20
三、解答题
9. (2024·安徽)如图6-21-21,☉O是△ABC的外接圆,D是直径AB上一点,∠ACD的平分线交AB于点E,交☉O于另一点F,FA=FE.
(1)求证:CD⊥AB;
(1)证明:∵FA=FE,∴∠FAE=∠FEA.
∵∠FAE=∠FCB,∠FEA=∠CEB,∴∠FCB=∠CEB.
∵CE平分∠ACD,∴∠ACE=∠DCE.
∵AB是☉O的直径,∴∠ACB=90°,即∠ACE+∠FCB=90°.
∴∠DCE+∠CEB=90°.∴∠CDE=90°.∴CD⊥AB.
图6-21-21
(2)作FM⊥AB,垂足为M,若OM=OE=1,求AC的长.
图6-21-21
10. (2024·浙江)如图6-21-22,在圆内接四边形ABCD中,AD(1)若∠AFE=60°,CD为直径,求∠ABD的度数;
图6-21-22
(1)解:∵CD为直径,
∴∠CAD=90°.
∵∠ADC=∠AFE=60°,
∴∠ACD=90°-∠ADC=30°.
∴∠ABD=∠ACD=30°.
(2)求证:①EF∥BC;
(2)证明:①∵四边形ABCD是圆内接四边形,
∴∠ADC+∠ABC=180°.
∵∠AFE=∠ADC,∴∠AFE+∠ABC=180°.∴EF∥BC.
图6-21-22
②EF=BD.
答图6-21-6
命题趋势
( 限时 5 分钟)
(教材改编)如图6-21-23,△ABC内接于☉O,连接AO并延长交BC于点D,且AD⊥BC于点D.
【知识技能】(1)如图6-21-23①,求证:∠B=∠C;
图6-21-23
(1)证明:∵AD⊥BC,AD过圆心O,
∴BD=CD.∴AB=AC.∴∠B=∠C.
答图6-21-7
【拓展探索】(3)如图6-21-23③,在(2)的条件下,过点A作AF⊥CE交CE的延长线于点F,若AE=5,AB=13,求AF的长.
答图6-21-8
命题解读:根据最新课程标准和近三年中考命题动向,预测2025年中考命题方向可能注重考查圆的基本概念、性质和定理,如圆的对称性、圆周角定理、垂径定理等;强调与三角形、四边形等几何图形的综合运用,可能涉及三角形的相似、三角函数等知识;还可能会考查综合探究类题型,通过变换图形位置或构造特殊图形综合考查.
第六章 圆
第21课时 圆的有关概念及性质
课前循环练
(限时5分钟)
A
D
C
4. (广东真题)如图6-21-1,在△ABC中,M,N分别是AB,AC的中点,且∠A+∠B=120°,则∠ANM= .
图6-21-1
60°
5. (广东真题)如图6-21-2,已知AB是☉O的直径,BC为弦,∠ABC=30°. 过圆心O作OD⊥BC交☉O于点D,连接DC,则∠DCB= .
图6-21-2
30°
①理解圆、弧、弦、圆心角、圆周角的概念,了解等圆、等弧的概念.
②探索并证明垂径定理:垂直于弦的直径平分弦以及弦所对的两条弧.
③探索圆周角与圆心角及其所对弧的关系,知道同弧(或等弧)所对的圆周角相等. 了解并证明圆周角定理及其推论:圆周角等于它所对弧上的圆心角的一半;直径所对的圆周角是直角,90°的圆周角所对的弦是直径;圆内接四边形的对角互补.
课标要求
对接教材 人教:九上第二十四章 圆
北师:九下第三章 圆
考点梳理
考点复习
1.圆
平面上到定点的距离等于定长的所有点组成的图形叫做圆.其中,定点称为 ,定长称为
圆心
半径
广东省对应考点例题
例1. 下列条件中,能确定一个圆的是 ( )
A.以点O为圆心
B.以2 cm长为半径
C.以点O为圆心,5 cm长为半径
D.经过点A
C
2.圆的对称性
(1)圆是轴对称图形,其对称轴是任意一条 的直线,有
条对称轴.
(2)圆是中心对称图形,对称中心为
过圆心
无数
圆心
例2. 下列说法中,不正确的是 ( )
A.圆是轴对称图形,有无数条对称轴
B.圆是中心对称图形,有无数个对称中心
C. 圆的任意一条直径所在直线都是圆的对称轴
D.圆既是轴对称图形,又是中心对称图形
B
3.与圆有关的概念
(1)弧:圆上任意 的部分叫做圆弧,简称弧.
(2)弦:连接圆上任意两点的 叫做弦.
(3)直径:经过 的弦叫做直径.
(4)圆心角:顶点在 的角叫做圆心角.
(5)圆周角:顶点在 ,两边分别与圆还有另一个交点.像这样的角,叫做圆周角
两点间
线段
圆心
圆心
圆上
例3. 下列命题:①圆上任意两点间的部分叫弧;②圆心角相等则它们所对的弧相等;③在同一个圆中,直径是最长的弦;④直径是圆的对称轴;⑤顶点在圆上的角是圆周角;⑥顶点在圆心的角是圆心角.
其中正确的有 ( )
A. ①③⑤ B. ②④⑥
C. ①③⑥ D. ②③⑤
C
4.圆心角、弧、弦之间的关系
(1)在同圆或等圆中,相等的圆心角所对的弧 ,所对的弦
.
(2)在同圆或等圆中,如果两个圆心角、两条弧、两条弦中有一组量相等,那么它们所对应的其余各组量都分别
相等
相等
相等
图6-21-3
D
5.垂径定理及其推论
(1)垂径定理:垂直于弦的直径 这条弦,并且 弦所对的弧.
(2)推论:①平分弦(不是直径)的直径 于弦,并且 弦所对的弧;
②弦的垂直平分线经过 ,并且平分弦所对的两条弧;
③平分弦所对的一条弧的直径 弦,并且 弦所对的另一条弧
平分
平分
垂直
平分
圆心
垂直平分
平分
图6-21-4
B
6.圆周角定理及其推论
(1)圆周角定理:圆周角的度数等于它所对弧上的圆心角度数的______
.
(2)推论:①同弧或等弧所对的圆周角 ;
②半圆(或直径)所对的圆周角是 ,90°的圆周角所对的弦是 ;
③圆内接四边形的对角
一半
相等
直角
直径
互补
例6. 如图6-21-5,四边形ABCD内接于☉O,E为DC延长线上一点,BF为☉O的直径,连接DF,DB,∠FBD=40°,则∠BCE的度数为 ( )
A. 40°
B. 50°
C. 60°
D. 130°
图6-21-5
B
广东中考
1. (2023·广东题9,3分,圆周角定理的推论)如图6-21-6,AB是☉O的直径,∠BAC=50°,则∠D= ( )
A. 20° B. 40°
C. 50° D. 80°
图6-21-6
B
图6-21-7
B
3. (2022·广东题22,12分,圆周角定理的推论;等腰直角三角形;勾股定理)如图6-21-8,四边形ABCD内接于☉O,AC为☉O的直径,∠ADB=∠CDB.
(1)试判断△ABC的形状,并给出证明;
图6-21-8
图6-21-8
高分击破
【典型考点】圆内接四边形的性质;翻折变换(折叠问题);圆周角定理
得分点分析
1. (2022·广东改编,综合探究)如图6-21-9①,已知四边形ABCD内接于☉O,AC为☉O的直径,∠BAC=∠ADB.
····································································
图6-21-9
(1)试说明△ABC的形状;
解:(1)∵AC为☉O的直径,
∴∠ABC=90°.
··············1分(利用“直径所对的圆周角是直角”得1分)
∵∠ADB=∠ACB,∠BAC=∠ADB,
··············2分(利用“同弧所对的圆周角相等”得1分)
∴∠BAC=∠ACB.∴AB=BC. ··················3分(利用等量代换,等角对等边得1分)
∴△ABC是等腰直角三角形. ··············4分(利用等腰直角三角形的判定得1分)
图6-21-9
图6-21-9
②将△ABD沿BD所在的直线折叠(如图6-21-9②),得到△A'BD,连接A'C,求∠BA'C的度数.
图6-21-9
∴折叠后,点A的对应点A'恰好落在DC上. ·······10分(确定点A'的位置得1分)
∵∠BAD=∠BAC+∠DAC=45°+60°=105°, ····························11分(求出∠BAD的度数得1分)
∴∠BA'D=∠BAD=105°. ···································12分(利用折叠的性质得1分)
∴∠BA'C=180°-∠BA'D=180°-105°=75°. ····························13分(求出∠BA'C的度数得1分)
图6-21-9
温馨提示:此类考题常见于广东省中考数学试卷的第22题,分值一般为13分,答题时要注意书写格式,分步书写,慢做会求全对,评卷老师是分步给分的哦!
【典型错例】无图题考察圆周角的应用时没有分类讨论导致漏解
2. 已知☉O是△ABC的外接圆,过顶点A,B分别作☉O的切线,它们交于点P,若∠APB=50°,求∠ACB的度数.
答图6-21-1
图6-21-10
图6-21-11
60°
120°
<
种子生长:垂径定理
(2)若AE=CD,BE=2,求☉O的半径;
答图6-21-2
生长变式:图形变式
(3)如图6-21-12,在(2)的条件下,延长AG,DC交于点F,连接DG.若G是AF的中点,求AG的长;
图6-21-12
解:如答图6-21-3,连接BG.
∵AB是☉O的直径,∴∠AGB=90°.∴∠B+∠BAG=90°.
∵AB⊥CD,∴∠AEF=90°.∴∠F+∠BAG=90°.
∴∠B=∠F.
∵∠ADG=∠B,∴∠ADG=∠F.
又∵∠DAG=∠FAD,∴△ADG∽△AFD.
答图6-21-3
答图6-21-3
答图6-21-4
答图6-21-4
答图6-21-5
中考演练
(限时15分钟)
一、选择题
1. (2024·湖南)如图6-21-13,AB,AC为☉O的两条弦,连接OB,OC.若∠A=45°,则∠BOC的度数为 ( )
A. 60° B. 75°
C. 90° D. 135°
图6-21-13
C
图6-21-14
B
图6-21-15
C
4. (2024·广元)如图6-21-16,已知四边形ABCD是☉O的内接四边形,E为AD延长线上一点,∠AOC=128°,则∠CDE等于 ( )
A. 64°
B. 60°
C. 54°
D. 52°
图6-21-16
A
5. (2024·通辽)如图6-21-17,圆形拱门最下端AB在地面上,D为AB的中点,C为拱门最高点,线段CD经过拱门所在圆的圆心.若AB=1 m,CD=2.5 m,则拱门所在圆的半径为 ( )
A. 1.25 m B. 1.3 m
C. 1.4 m D. 1.45 m
图6-21-17
B
二、填空题
6. (2024·苏州)如图6-21-18,△ABC是☉O的内接三角形,若∠OBC=28°,则∠A= °.
图6-21-18
62
7. (2024·巴中)如图6-21-19,四边形ABCD为☉O的内接四边形. 若四边形ABCO为菱形,则∠ADC的大小为 .
图6-21-19
60°
8. (2024·牡丹江)如图6-21-20,在☉O中,直径AB⊥CD于点E,CD=6,BE=1,则弦AC的长为 .
图6-21-20
三、解答题
9. (2024·安徽)如图6-21-21,☉O是△ABC的外接圆,D是直径AB上一点,∠ACD的平分线交AB于点E,交☉O于另一点F,FA=FE.
(1)求证:CD⊥AB;
(1)证明:∵FA=FE,∴∠FAE=∠FEA.
∵∠FAE=∠FCB,∠FEA=∠CEB,∴∠FCB=∠CEB.
∵CE平分∠ACD,∴∠ACE=∠DCE.
∵AB是☉O的直径,∴∠ACB=90°,即∠ACE+∠FCB=90°.
∴∠DCE+∠CEB=90°.∴∠CDE=90°.∴CD⊥AB.
图6-21-21
(2)作FM⊥AB,垂足为M,若OM=OE=1,求AC的长.
图6-21-21
10. (2024·浙江)如图6-21-22,在圆内接四边形ABCD中,AD
图6-21-22
(1)解:∵CD为直径,
∴∠CAD=90°.
∵∠ADC=∠AFE=60°,
∴∠ACD=90°-∠ADC=30°.
∴∠ABD=∠ACD=30°.
(2)求证:①EF∥BC;
(2)证明:①∵四边形ABCD是圆内接四边形,
∴∠ADC+∠ABC=180°.
∵∠AFE=∠ADC,∴∠AFE+∠ABC=180°.∴EF∥BC.
图6-21-22
②EF=BD.
答图6-21-6
命题趋势
( 限时 5 分钟)
(教材改编)如图6-21-23,△ABC内接于☉O,连接AO并延长交BC于点D,且AD⊥BC于点D.
【知识技能】(1)如图6-21-23①,求证:∠B=∠C;
图6-21-23
(1)证明:∵AD⊥BC,AD过圆心O,
∴BD=CD.∴AB=AC.∴∠B=∠C.
答图6-21-7
【拓展探索】(3)如图6-21-23③,在(2)的条件下,过点A作AF⊥CE交CE的延长线于点F,若AE=5,AB=13,求AF的长.
答图6-21-8
命题解读:根据最新课程标准和近三年中考命题动向,预测2025年中考命题方向可能注重考查圆的基本概念、性质和定理,如圆的对称性、圆周角定理、垂径定理等;强调与三角形、四边形等几何图形的综合运用,可能涉及三角形的相似、三角函数等知识;还可能会考查综合探究类题型,通过变换图形位置或构造特殊图形综合考查.
同课章节目录
