中考数学复习知识梳理第二章方程(组)与不等式(组)第8课时一元一次不等式(组)及其应用课件(共38张PPT)
文档属性
| 名称 | 中考数学复习知识梳理第二章方程(组)与不等式(组)第8课时一元一次不等式(组)及其应用课件(共38张PPT) |  | |
| 格式 | ppt | ||
| 文件大小 | 4.3MB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 通用版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2025-05-31 09:49:03 | ||
图片预览









文档简介
(共38张PPT)
第二章 方程(组)与不等式(组)
第8课时 一元一次不等式(组)及其应用
课前循环练
(限时5分钟)
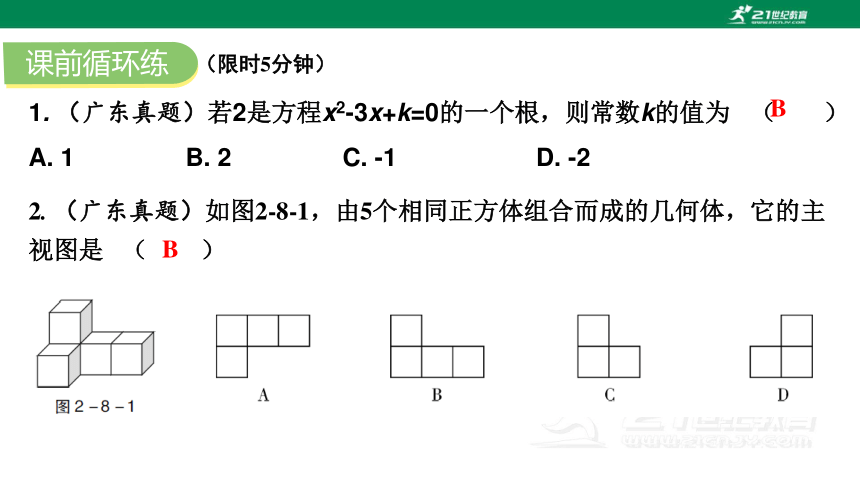
1. (广东真题)若2是方程x2-3x+k=0的一个根,则常数k的值为 ( )
A. 1 B. 2 C. -1 D. -2
B
2. (广东真题)如图2-8-1,由5个相同正方体组合而成的几何体,它的主视图是 ( )
B
A
20
-3①结合具体问题,了解不等式的意义, 探索不等式的基本性质.
②能解数字系数的一元一次不等式,并能在数轴上表示出解集;会用数轴确定两个一元一次不等式组成的不等式组的解集.
③能根据具体问题中的数量关系,列出一元一次不等式,解决简单的问题.
课标要求
对接教材 人教:七下第九章 不等式与不等式组
北师:八下第二章 一元一次不等式与一元一次不等式组
考点梳理
不变
>
不变
>
>
改变
<
<
<
>
<
2.一元一次不等式
含有 未知数,未知数的次数是1且不等号两边都是整式的不等式,叫做一元一次不等式
一个
例2. 下列式子:
① -5<0;② 2x=3;
③ 3x-1>2;④ 4x-2y≤0;
⑤ x2-3x+2>0;⑥ x-2y.
其中属于不等式的是 ,属于一元一次不等式的是 .(填序号)
①③④⑤
③
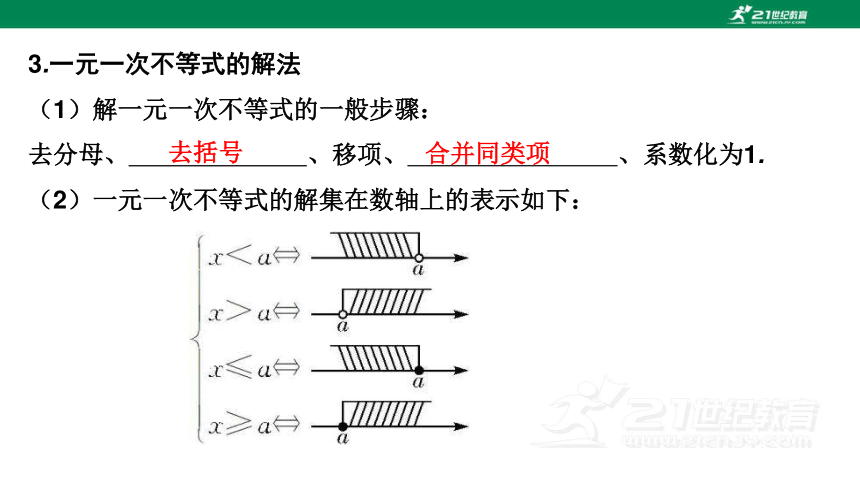
3.一元一次不等式的解法
(1)解一元一次不等式的一般步骤:
去分母、 、移项、 、系数化为1.
(2)一元一次不等式的解集在数轴上的表示如下:
去括号
合并同类项
解:去分母,得
2(2-3x)>10-5(1+x).
去括号,得4-6x>10-5-5x.
移项,得-6x+5x>10-5-4.
合并同类项,得-x>1.
系数化为1,得x<-1.
在数轴上表示解集如答图2-8-1.
答图2-8-1
4.一元一次不等式组
(1)概念:一般地,关于同一个未知数的几个一元一次不等式合在一起,就组成一个一元一次不等式组.
(2)解集:一元一次不等式组中各个不等式的解集的 ,叫做这个一元一次不等式组的解集.
公共部分
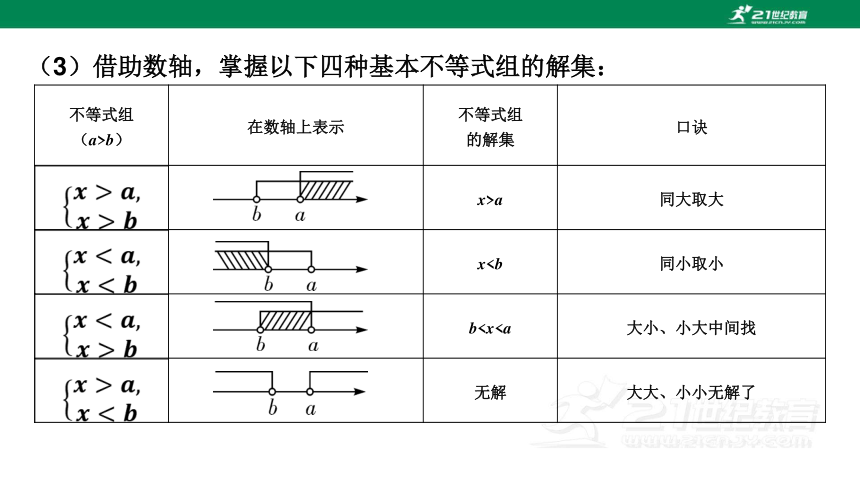
(3)借助数轴,掌握以下四种基本不等式组的解集:
不等式组
(a>b) 在数轴上表示 不等式组
的解集 口诀
x>a 同大取大
xb无解 大大、小小无解了
答图2-8-2
5.一元一次不等式(组)的应用
列一元一次不等式解应用题时,应注意抓住题中的关键词.下面是一些常见的关键词:
常见关键词 符号
大于、多于、超过、高于
小于、少于、不足、低于
至少、不低于、不小于、不少于
最多、不超过、不高于、不大于
>
<
≥
≤
例5.某校组织开展了“防疫从我做起”知识竞赛,共有20道题.答对一题加10分,答错(或不答)一题扣5分.如果小华参加本次竞赛得分要不低于140分,那么他最多答错(或不答)多少道题?
解:设小华答错(或不答)x道题,则答对(20-x)道题.
由题意,得10(20-x)-5x≥140.
解得x≤4.
答:小华最多答错(或不答)4道题.
广东中考
D
2. (2024·广东题12,3分,在数轴上表示不等式组的解集)关于x的不等式组中,两个不等式的解集如图2-8-3所示,则这个不等式组的解集是
.
x≥3
图2-8-3
3. (2023·广东题14,3分,一元一次不等式的应用)某商品进价4元,标价5元出售,商家准备打折销售,但其利润率不能少于10%,则最多可打
折.
八八
高分击破
温馨提示:此类考题常见于广东省中考数学试卷的第16题,分值一般为7分,答题时要注意书写格式,分步书写,慢做会求全对,评卷老师是分步给分的哦!
【典型考点】一元一次不等式的应用
2. (2023·深圳)某商场在世博会上购置A,B两种玩具,其中B玩具的单价比A玩具的单价贵25元,且购置2个B玩具与1个A玩具共花费200元.
(1)求A,B玩具的单价;
解:(1)设A玩具的单价为x元,则B玩具的单价为(x+25)元.
由题意,得2(x+25)+x=200.
解得x=50.
则x+25=50+25=75.
答:A玩具的单价为50元,B玩具的单价为75元.
(2)若该商场要求购置B玩具的数量是A玩具数量的2倍,且购置玩具的总额不高于20 000元,则该商场最多可以购置多少个A玩具?
(2)设该商场可以购置y个A玩具.
由题意,得50y+75×2y≤20 000.
解得y≤100.
答:该商场最多可以购置100个A玩具.
解不等式②,得1-x<2.
∴-x<1.
∴x>-1.
∴原不等式组的解集为x>-1.
错解分析
错解:解不等式①,得2+x>-1.
∴x>-3.
解不等式②,得1-x>2.
∴-x>1.∴x>-1.
∴原不等式组的解集是x>-1.
剖析:上面的解答过程中,解不等式①时,由2(1+x)得2+x是错误的,应依据乘法分配律进行去括号;解不等式②时,由-(1-x)>-2,得1-x>2,以及由-x>1,得x>-1都是错误的,不等式两边都乘(除以)-1,不等号的方向应该改变.
1种子生长:不等式组的整数解
(2)若不等式组有5个整数解,求a的取值范围;
生长变式:不等式组变式
(3)对于任意实数m,n,定义一种新运算:m※n=mn-m-n+2,等式的右边是通常的乘法和加减运算. 例如:2※6=2×6-2-6+2=6. 请根据上述定义解决问题:若k<4※x<7,且解集中有3个整数解,求k的取值范围;
种子成树:综合创新
(4)某中学组织学生研学,原计划租用可坐乘客45人的A种客车若干辆,则有30人没有座位;若租用可坐乘客60人的B种客车,则可少租6辆,且恰好坐满.
①原计划租用A种客车多少辆?这次研学去了多少人?
解:①设原计划租用A种客车x辆.
由题意,得45x+30=60(x-6).
解得x=26.
则60(x-6)=60×(26-6)=1 200.
答:原计划租用A种客车26辆,这次研学去了1 200人.
②若该校计划租用A,B两种客车共25辆,要求B种客车不超过7辆,且每人都有座位,则有哪几种租车方案?
∴共有下面3种租车方案:
方案一:租用5辆B种客车,20辆A种客车;
方案二:租用6辆B种客车,19辆A种客车;
方案三:租用7辆B种客车,18辆A种客车.
中考演练
(限时15分钟)
一、选择题
1. (2024·广州)若aA. a+3>b+3 B. a-2>b-2 C. -a<-b D. 2a<2b
2. (2024·陕西)不等式2(x-1)≥6的解集是 ( )
A. x≤2 B. x≥2 C. x≤4 D. x≥4
D
D
B
4. (2023·丽水)小霞原有存款52元,小明原有存款70元. 从这个月开始,小霞每月存15元零花钱,小明每月存12元零花钱,设经过n个月后小霞的存款超过小明,可列不等式为 ( )
A. 52+15n>70+12n B. 52+15n<70+12n
C. 52+12n>70+15n D. 52+12n<70+15n
A
B
x<1
2解:去分母,得2(x+1)-6≤
3(2-x).
去括号,得2x+2-6≤6-3x.
移项,得2x+3x≤6-2+6.
合并同类项,得5x≤10.
系数化为1,得x≤2.
在数轴上表示解集如答图2-8-3.
答图2-8-3
命题趋势
(限时 5 分钟)
(原创题)某新能源4S店准备购进甲、乙两种新能源车进行销售,其中每辆甲种新能源车的进价比每辆乙种新能源车的进价少2万元,且用80万元购进甲种新能源车的数量与用100万元购进乙种新能源车的数量相同.
(1)求甲、乙两种新能源车的进价分别是每辆多少万元;
(2)若该新能源4S店购进甲种新能源车的数量比乙种新能源车的数量的3倍还少5辆,且购进甲、乙两种新能源车的总数量不超过95辆,则新能源4S店最多购进乙种新能源车多少辆?
(2)设新能源4S店购进乙种新能源车y辆,则购进甲种新能源车(3y-5)辆.
由题意,得3y-5+y≤95.
解得y≤25.
答:新能源4S店最多购进乙种新能源车25辆.
(3)在(2)的条件下,如果甲、乙两种新能源车的售价分别是12万元/辆和15万元/辆,且将购进的甲、乙两种新能源车全部售出后,可使销售两种新能源车的总利润超过380万元,那么该新能源4S店购进甲、乙两种新能源车有哪几种方案?
命题解读:根据最新课程标准和近三年中考命题动向,预测2025年中考命题方向可能注重考查不等式(组)的基本概念和解法,如解不等式(组)并在数轴上表示解集;强调不等式(组)在实际问题中的应用,如涉及商品销售、购进方案、方案设计等情境;可能会与方程、函数等知识综合考查,还可能会出现定义新运算等创新题型.
第二章 方程(组)与不等式(组)
第8课时 一元一次不等式(组)及其应用
课前循环练
(限时5分钟)
1. (广东真题)若2是方程x2-3x+k=0的一个根,则常数k的值为 ( )
A. 1 B. 2 C. -1 D. -2
B
2. (广东真题)如图2-8-1,由5个相同正方体组合而成的几何体,它的主视图是 ( )
B
A
20
-3
②能解数字系数的一元一次不等式,并能在数轴上表示出解集;会用数轴确定两个一元一次不等式组成的不等式组的解集.
③能根据具体问题中的数量关系,列出一元一次不等式,解决简单的问题.
课标要求
对接教材 人教:七下第九章 不等式与不等式组
北师:八下第二章 一元一次不等式与一元一次不等式组
考点梳理
不变
>
不变
>
>
改变
<
<
<
>
<
2.一元一次不等式
含有 未知数,未知数的次数是1且不等号两边都是整式的不等式,叫做一元一次不等式
一个
例2. 下列式子:
① -5<0;② 2x=3;
③ 3x-1>2;④ 4x-2y≤0;
⑤ x2-3x+2>0;⑥ x-2y.
其中属于不等式的是 ,属于一元一次不等式的是 .(填序号)
①③④⑤
③
3.一元一次不等式的解法
(1)解一元一次不等式的一般步骤:
去分母、 、移项、 、系数化为1.
(2)一元一次不等式的解集在数轴上的表示如下:
去括号
合并同类项
解:去分母,得
2(2-3x)>10-5(1+x).
去括号,得4-6x>10-5-5x.
移项,得-6x+5x>10-5-4.
合并同类项,得-x>1.
系数化为1,得x<-1.
在数轴上表示解集如答图2-8-1.
答图2-8-1
4.一元一次不等式组
(1)概念:一般地,关于同一个未知数的几个一元一次不等式合在一起,就组成一个一元一次不等式组.
(2)解集:一元一次不等式组中各个不等式的解集的 ,叫做这个一元一次不等式组的解集.
公共部分
(3)借助数轴,掌握以下四种基本不等式组的解集:
不等式组
(a>b) 在数轴上表示 不等式组
的解集 口诀
x>a 同大取大
xb
答图2-8-2
5.一元一次不等式(组)的应用
列一元一次不等式解应用题时,应注意抓住题中的关键词.下面是一些常见的关键词:
常见关键词 符号
大于、多于、超过、高于
小于、少于、不足、低于
至少、不低于、不小于、不少于
最多、不超过、不高于、不大于
>
<
≥
≤
例5.某校组织开展了“防疫从我做起”知识竞赛,共有20道题.答对一题加10分,答错(或不答)一题扣5分.如果小华参加本次竞赛得分要不低于140分,那么他最多答错(或不答)多少道题?
解:设小华答错(或不答)x道题,则答对(20-x)道题.
由题意,得10(20-x)-5x≥140.
解得x≤4.
答:小华最多答错(或不答)4道题.
广东中考
D
2. (2024·广东题12,3分,在数轴上表示不等式组的解集)关于x的不等式组中,两个不等式的解集如图2-8-3所示,则这个不等式组的解集是
.
x≥3
图2-8-3
3. (2023·广东题14,3分,一元一次不等式的应用)某商品进价4元,标价5元出售,商家准备打折销售,但其利润率不能少于10%,则最多可打
折.
八八
高分击破
温馨提示:此类考题常见于广东省中考数学试卷的第16题,分值一般为7分,答题时要注意书写格式,分步书写,慢做会求全对,评卷老师是分步给分的哦!
【典型考点】一元一次不等式的应用
2. (2023·深圳)某商场在世博会上购置A,B两种玩具,其中B玩具的单价比A玩具的单价贵25元,且购置2个B玩具与1个A玩具共花费200元.
(1)求A,B玩具的单价;
解:(1)设A玩具的单价为x元,则B玩具的单价为(x+25)元.
由题意,得2(x+25)+x=200.
解得x=50.
则x+25=50+25=75.
答:A玩具的单价为50元,B玩具的单价为75元.
(2)若该商场要求购置B玩具的数量是A玩具数量的2倍,且购置玩具的总额不高于20 000元,则该商场最多可以购置多少个A玩具?
(2)设该商场可以购置y个A玩具.
由题意,得50y+75×2y≤20 000.
解得y≤100.
答:该商场最多可以购置100个A玩具.
解不等式②,得1-x<2.
∴-x<1.
∴x>-1.
∴原不等式组的解集为x>-1.
错解分析
错解:解不等式①,得2+x>-1.
∴x>-3.
解不等式②,得1-x>2.
∴-x>1.∴x>-1.
∴原不等式组的解集是x>-1.
剖析:上面的解答过程中,解不等式①时,由2(1+x)得2+x是错误的,应依据乘法分配律进行去括号;解不等式②时,由-(1-x)>-2,得1-x>2,以及由-x>1,得x>-1都是错误的,不等式两边都乘(除以)-1,不等号的方向应该改变.
1
(2)若不等式组有5个整数解,求a的取值范围;
生长变式:不等式组变式
(3)对于任意实数m,n,定义一种新运算:m※n=mn-m-n+2,等式的右边是通常的乘法和加减运算. 例如:2※6=2×6-2-6+2=6. 请根据上述定义解决问题:若k<4※x<7,且解集中有3个整数解,求k的取值范围;
种子成树:综合创新
(4)某中学组织学生研学,原计划租用可坐乘客45人的A种客车若干辆,则有30人没有座位;若租用可坐乘客60人的B种客车,则可少租6辆,且恰好坐满.
①原计划租用A种客车多少辆?这次研学去了多少人?
解:①设原计划租用A种客车x辆.
由题意,得45x+30=60(x-6).
解得x=26.
则60(x-6)=60×(26-6)=1 200.
答:原计划租用A种客车26辆,这次研学去了1 200人.
②若该校计划租用A,B两种客车共25辆,要求B种客车不超过7辆,且每人都有座位,则有哪几种租车方案?
∴共有下面3种租车方案:
方案一:租用5辆B种客车,20辆A种客车;
方案二:租用6辆B种客车,19辆A种客车;
方案三:租用7辆B种客车,18辆A种客车.
中考演练
(限时15分钟)
一、选择题
1. (2024·广州)若a
2. (2024·陕西)不等式2(x-1)≥6的解集是 ( )
A. x≤2 B. x≥2 C. x≤4 D. x≥4
D
D
B
4. (2023·丽水)小霞原有存款52元,小明原有存款70元. 从这个月开始,小霞每月存15元零花钱,小明每月存12元零花钱,设经过n个月后小霞的存款超过小明,可列不等式为 ( )
A. 52+15n>70+12n B. 52+15n<70+12n
C. 52+12n>70+15n D. 52+12n<70+15n
A
B
x<1
2
3(2-x).
去括号,得2x+2-6≤6-3x.
移项,得2x+3x≤6-2+6.
合并同类项,得5x≤10.
系数化为1,得x≤2.
在数轴上表示解集如答图2-8-3.
答图2-8-3
命题趋势
(限时 5 分钟)
(原创题)某新能源4S店准备购进甲、乙两种新能源车进行销售,其中每辆甲种新能源车的进价比每辆乙种新能源车的进价少2万元,且用80万元购进甲种新能源车的数量与用100万元购进乙种新能源车的数量相同.
(1)求甲、乙两种新能源车的进价分别是每辆多少万元;
(2)若该新能源4S店购进甲种新能源车的数量比乙种新能源车的数量的3倍还少5辆,且购进甲、乙两种新能源车的总数量不超过95辆,则新能源4S店最多购进乙种新能源车多少辆?
(2)设新能源4S店购进乙种新能源车y辆,则购进甲种新能源车(3y-5)辆.
由题意,得3y-5+y≤95.
解得y≤25.
答:新能源4S店最多购进乙种新能源车25辆.
(3)在(2)的条件下,如果甲、乙两种新能源车的售价分别是12万元/辆和15万元/辆,且将购进的甲、乙两种新能源车全部售出后,可使销售两种新能源车的总利润超过380万元,那么该新能源4S店购进甲、乙两种新能源车有哪几种方案?
命题解读:根据最新课程标准和近三年中考命题动向,预测2025年中考命题方向可能注重考查不等式(组)的基本概念和解法,如解不等式(组)并在数轴上表示解集;强调不等式(组)在实际问题中的应用,如涉及商品销售、购进方案、方案设计等情境;可能会与方程、函数等知识综合考查,还可能会出现定义新运算等创新题型.
同课章节目录
