中考数学复习知识梳理第二章方程(组)与不等式(组)第7课时一元二次方程及其应用课件(共43张PPT)
文档属性
| 名称 | 中考数学复习知识梳理第二章方程(组)与不等式(组)第7课时一元二次方程及其应用课件(共43张PPT) |

|
|
| 格式 | ppt | ||
| 文件大小 | 3.2MB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 通用版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2025-05-31 09:45:33 | ||
图片预览











文档简介
(共43张PPT)
第二章 方程(组)与不等式(组)
第7课时 一元二次方程及其应用
课前循环练
(限时5分钟)
1. (广东真题)下列所述图形中,既是中心对称图形,又是轴对称图形的是 ( )
A. 矩形 B. 平行四边形 C. 正五边形 D. 正三角形
A
2. (广东真题)如图2-7-1,直线a∥b,∠1=40°,则∠2= ( )
A. 30°
B. 40°
C. 50°
D. 60°
B
B
x>3
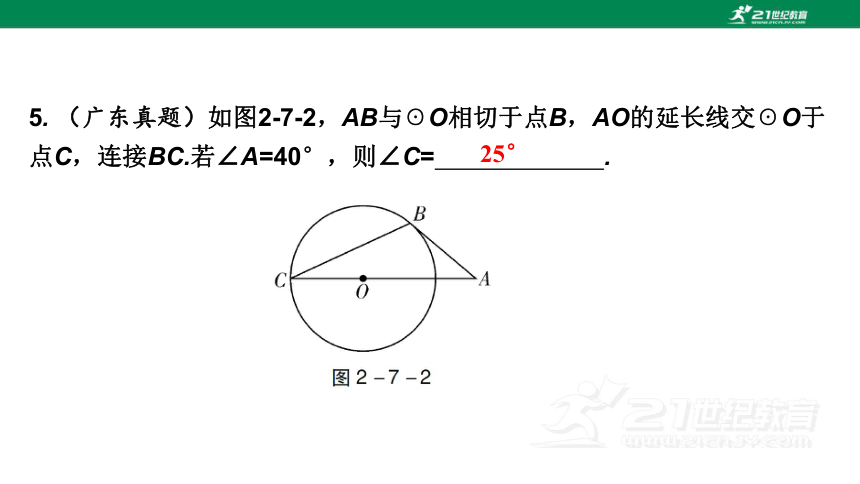
5. (广东真题)如图2-7-2,AB与☉O相切于点B,AO的延长线交☉O于点C,连接BC.若∠A=40°,则∠C= .
25°
①能根据现实情境理解方程的意义,能针对具体问题列出方程;理解方程解的意义,经历估计方程解的过程.
②理解配方法,能用配方法、公式法、因式分解法解数字系数的一元二次方程.
③会用一元二次方程根的判别式判别方程是否有实根及两个实根是否相等.
④了解一元二次方程的根与系数的关系.
课标要求
对接教材 人教:九上第二十一章 一元二次方程
北师:九上第二章 一元二次方程
考点梳理
考点复习
1.一元二次方程
(1)等号两边都是 ,只含有 个未知数,并且未知数的最高次数是 的方程,叫做一元二次方程.
(2)一般形式:ax2+bx+c=0(a,b,c为常数,a≠0)
整式
一
2
③
2.用直接开平方法解一元二次方程
形如(x+m)2=n(n≥0)的方程,两边开平方转化为两个一元一次方程求解
例2. 填空(直接开平方法):
(1)方程x2=49的根是 ;
(2)方程2x2=6的根是 ;
(3)方程(x-1)2=2的根是 .
x1=7,x2=-7
3.用配方法解一元二次方程
把一元二次方程ax2+bx+c=0(a≠0)通过配方化成(x+m)2=n(n≥0)的形式,再直接开平方
例3. 用配方法解方程:2x2-5x-3=0.
解:方程两边同除以2,得 .
移项,得 .
配方,得 .
两边开平方,得 .
∴x1= ,x2= .
3
4.用公式法解一元二次方程
当一元二次方程ax2+bx+c=0(a≠0)满足b2-4ac≥0时,可利用求根公式
x= 求解
28
5.用因式分解法解一元二次方程
当一元二次方程的一边为0,而另一边易分解成两个一次因式的乘积时,即可化为两个一次式的乘积等于0的形式,再使这两个一次式分别等于0,得到两个一元一次方程,解之即可
x2-x=0
x(x-1)
x
x-1
0
1
6.一元二次方程根的判别式
叫做一元二次方程ax2+bx+c=0(a≠0)根的判别式,通常用希腊字母“Δ”表示它.判别式的符号决定了方程根的情况,具体如下:
Δ>0 方程有两个 的实数根;
Δ=0 方程有两个 的实数根;
Δ<0 方程 实数根
b2-4ac
不相等
相等
没有
例6. 已知关于x的方程x2-4x+k=0.
(1)当k 时,方程有实数根;
(2)当k 时,方程有两个相等的实数根;
(3)当k 时,方程没有实数根.
≤4
=4
>4
7.一元二次方程根与系数的关系
若一元二次方程ax2+bx+c=0(a≠0)有两个实数根x1,x2,则
x1+x2= ,x1x2=
例7. 已知α,β是方程x2+2x-5=0的两根,则
(1)α+β= ;
(2)αβ= .
-2
-5
8.一元二次方程的应用
(1)变化率问题
①设a为基础量,m为平均增长率,n为增长次数,b为增长后的量,则b=a(1+m)n;
②设a为基础量,p为平均下降率,q为下降次数,c为下降后的量,则c=
.
a(1-p)q
(2)传播问题
设a为传播源数,m为每个传播源每轮传播的数量,n为传播的轮次,b为传播后的总数量.
分析如下:
a a+am a+am+m
(a+am)=a(1+m)2
总结:b= .
a(1+m)n
(5)面积问题
注:图形经过移动,它的面积大小不会改变.
设图①、图②、图③中大矩形的长为a,宽为b,阴影部分的宽为x;图④是由一面墙和篱笆围成,设篱笆总长度为m,平行于墙的一边长为y.
①S空白=
②S空白=
③S空白=
④S空白=
(a-2x)(b-2x)
(a-x)(b-x)
(a-x)(b-x)
(6)动点问题:
①一般设运动时间为t,表示出动点运动的距离;
②通过几何性质表示出其他所需的线段;
③根据面积、勾股定理等数量关系建立方程;
④通过解方程找出动点的位置或其他相关信息
例8.(1)某厂今年一月份的总产量为500 t,三月份的总产量为720 t,平均每月增长率是x,则可列方程为 ( )
A. 500(1+2x)=720
B. 720(1+x)2=500
C. 500(1+x2)=720
D. 500(1+x)2=720
D
(2)有一人患流感,经过两轮传染后共有121人患了流感,求每轮传染中平均一个人传染了几个人.如果设每轮传染中平均一个人传染了x个人,那么依题意可得方程为 ( )
A. 1+x+x2=121
B. 1+x+x(1+x)=121
C. x2=121
D. 1+2x=121
B
A
(4)某商场销售一款毛衣,平均每天可售出30件,每件获利28元.受气温影响,商场决定适当降价出售.据调查,毛衣单价每降低1元,每天可多售出3件.要使每天获利1 080元,每件应降价多少元?设每件降价x元,则可列方程为 .
(28-x)(30+3x)=1 080
(5)如图2-7-3,在长为30 m,宽为20 m的长方形田地中开辟三条入口宽度相等的道路,已知剩余田地的面积为468 m2,求道路的宽度.设道路的宽度为x m,则可列方程为 .
(30-2x)(20-x)=468
广东中考
1. (2024·广东题13,3分,根的判别式)若关于x的一元二次方程x2+2x+c=0有两个相等的实数根,则c= .
2. (2022·广东题14,3分,一元二次方程的解)若x=1是方程x2-2x+a=0的根,则a= .
3. (2021·广东题14,4分,一元二次方程根与系数的关系)若一元二次方程x2+bx+c=0(b,c为常数)的两根x1,x2满足-31
1
x2-2=0(答案不唯一)
高分击破
温馨提示:此类考题可能见于广东省中考数学试卷的第17题,分值一般为7分,答题时要注意书写格式,分步书写,慢做会求全对,评卷老师是分步给分的哦!
【典型考点】一元二次方程的应用
2. (2024·深圳模拟)某品牌画册每本成本为40元,当售价为60元时,平均每天的销售量为100本. 为了吸引消费者,商家决定采取降价措施. 经试销统计发现,当画册售价每降低1元时,平均每天就能多售出10本. 设这种画册每本降价x元.
(1)平均每天的销售量为 本;(用含x的代数式表示)
(100+10x)
(2)商家想要使这种画册的销售利润平均每天达到2 240元,且要求每本售价不低于55元,求每本画册应降价多少元.
解:(2)由题意,得(60-40-x)(100+10x)=2 240.
整理,得x2-10x+24=0.
解得x1=4,x2=6.
∵要求每本售价不低于55元,∴60-x≥55,即x≤5.∴x=4.
答:每本画册应降价4元.
【典型错例】用配方法时,配方前没有把二次项系数化为1而导致配方错误
3. 用配方法解方程:2x2-8x+3=0.
【生长式训练】知识生长→变式创新
4. (中考创新,原创题)已知a,b是关于x的一元二次方程x2-18x+3m=0(m>0)的两个实数根.
知识种子:基本概念
(1)m的取值范围是 ;
0生长变式:求值变式
(3)若(a-1)(b-1)=13,求m的值;
解:由题意,得a+b=18,ab=3m.
∵(a-1)(b-1)=ab-(a+b)+1=13,
∴3m-18+1=13. 解得m=10.
∴m的值为10.
种子成树:综合创新
(4)为了便于劳动课程的开展,学校打算建一个矩形生态园ABCD(如图2-7-5),生态园一面靠墙(墙长9 m),另外三面用篱笆围成. 已知当AD的长为a m,CD的长为b m时,生态园的面积为80 m2,求此时AD的长.
解:由题意,得a+b=18.
∴b=18-a.
∵四边形ABCD是矩形,
∴BC=AD=a m,AB=CD=(18-a) m.
∵生态园的面积为80 m2,
∴a(18-a)=80. 解得a1=8,a2=10.
当a=8时,AB=18-a=10>9,不合题意,舍去;
当a=10时,AB=18-a=8<9,符合题意.
答:此时AD的长为10 m.
中考演练
(限时15分钟)
B
A
B
4. (2024·牡丹江)一种药品原价每盒48元,经过两次降价后每盒27元,两次降价的百分率相同,则每次降价的百分率为 ( )
A. 20% B. 22% C. 25% D. 28%
C
5. (2024·通辽)如图2-7-6,小程的爸爸用一段10 m长的铁丝网围成一个一边靠墙(墙长5.5 m)的矩形鸭舍,其面积为15 m2,在鸭舍侧面中间位置留一个1 m宽的门(由其他材料制成),则BC长为 ( )
A. 5 m或6 m
B. 2.5 m或3 m
C. 5 m
D. 3 m
C
二、填空题
6. (2024·深圳)一元二次方程x2-3x+a=0的一个解为x=1,则a= .
7. (2024·新疆)关于x的一元二次方程x2+3x+k=0有两个不相等的实数根,
则k的取值范围为 .
8. (2024·烟台)若一元二次方程2x2-4x-1=0的两根为m,n,则3m2-4m+n2的值为 .
2
6
10. (2023·郴州)随旅游旺季的到来,某景区游客人数逐月增加,2月份游客人数为1.6万人,4月份游客人数为2.5万人.
(1)求这两个月中该景区游客人数的月平均增长率;
解:(1)设这两个月中该景区游客人数的月平均增长率为x.
由题意,得1.6(1+x)2=2.5.
解得x1=0.25=25%,x2=-2.25(不合题意,舍去).
答:这两个月中该景区游客人数的月平均增长率为25%.
(2)预计5月份该景区游客人数会继续增长,但增长率不会超过前两个月的月平均增长率. 已知该景区5月1日至5月21日已接待游客2.125万人,则5月份后10天日均接待游客人数最多是多少万人?
(2)设5月份后10天日均接待游客人数是a万人.
由题意,得2.125+10a≤2.5×(1+25%).
解得a≤0.1.
答:5月份后10天日均接待游客人数最多是0.1万人.
命题趋势
(限时 5 分钟)
(原创题)某商店以每件45元的价格购进某款学习软件,以每件68元的价格出售,经统计,5月份的销售量为256件,7月份的销售量为400件.
(1)求该款学习软件6,7月份销售量的月平均增长率;
解:(1)设该款学习软件6,7月份销售量的月平均增长率为x.
由题意,得256(1+x)2=400.
解得x1=0.25=25%,x2=-2.25(不合题意,舍去).
答:该款学习软件6,7月份销售量的月平均增长率为25%.
(2)经市场预测,8月份的销售量将与7月份持平,为减少库存,商店决定降价促销. 调查发现,该款学习软件每降价1元,月销售量就会增加20件. 当该款学习软件降价多少元时,月销售利润达到8 400元?
(2)设该款学习软件降价m元.
由题意,得(68-45-m)(400+20m)=8 400.
整理,得m2-3m-40=0.
解得m1=8,m2=-5(不合题意,舍去).
答:当该款学习软件降价8元时,月销售利润达到8 400元.
命题解读:根据最新课程标准和近三年中考命题动向,预测2025年中考命题方向可能注重考查对一元二次方程基本概念的理解,如根的判别式、方程的解、根与系数的关系等;强调运用公式法、配方法等解一元二次方程;注重一元二次方程在实际问题中的应用,如利润、增长率等问题;还可能会与函数、几何等知识点综合考查.
第二章 方程(组)与不等式(组)
第7课时 一元二次方程及其应用
课前循环练
(限时5分钟)
1. (广东真题)下列所述图形中,既是中心对称图形,又是轴对称图形的是 ( )
A. 矩形 B. 平行四边形 C. 正五边形 D. 正三角形
A
2. (广东真题)如图2-7-1,直线a∥b,∠1=40°,则∠2= ( )
A. 30°
B. 40°
C. 50°
D. 60°
B
B
x>3
5. (广东真题)如图2-7-2,AB与☉O相切于点B,AO的延长线交☉O于点C,连接BC.若∠A=40°,则∠C= .
25°
①能根据现实情境理解方程的意义,能针对具体问题列出方程;理解方程解的意义,经历估计方程解的过程.
②理解配方法,能用配方法、公式法、因式分解法解数字系数的一元二次方程.
③会用一元二次方程根的判别式判别方程是否有实根及两个实根是否相等.
④了解一元二次方程的根与系数的关系.
课标要求
对接教材 人教:九上第二十一章 一元二次方程
北师:九上第二章 一元二次方程
考点梳理
考点复习
1.一元二次方程
(1)等号两边都是 ,只含有 个未知数,并且未知数的最高次数是 的方程,叫做一元二次方程.
(2)一般形式:ax2+bx+c=0(a,b,c为常数,a≠0)
整式
一
2
③
2.用直接开平方法解一元二次方程
形如(x+m)2=n(n≥0)的方程,两边开平方转化为两个一元一次方程求解
例2. 填空(直接开平方法):
(1)方程x2=49的根是 ;
(2)方程2x2=6的根是 ;
(3)方程(x-1)2=2的根是 .
x1=7,x2=-7
3.用配方法解一元二次方程
把一元二次方程ax2+bx+c=0(a≠0)通过配方化成(x+m)2=n(n≥0)的形式,再直接开平方
例3. 用配方法解方程:2x2-5x-3=0.
解:方程两边同除以2,得 .
移项,得 .
配方,得 .
两边开平方,得 .
∴x1= ,x2= .
3
4.用公式法解一元二次方程
当一元二次方程ax2+bx+c=0(a≠0)满足b2-4ac≥0时,可利用求根公式
x= 求解
28
5.用因式分解法解一元二次方程
当一元二次方程的一边为0,而另一边易分解成两个一次因式的乘积时,即可化为两个一次式的乘积等于0的形式,再使这两个一次式分别等于0,得到两个一元一次方程,解之即可
x2-x=0
x(x-1)
x
x-1
0
1
6.一元二次方程根的判别式
叫做一元二次方程ax2+bx+c=0(a≠0)根的判别式,通常用希腊字母“Δ”表示它.判别式的符号决定了方程根的情况,具体如下:
Δ>0 方程有两个 的实数根;
Δ=0 方程有两个 的实数根;
Δ<0 方程 实数根
b2-4ac
不相等
相等
没有
例6. 已知关于x的方程x2-4x+k=0.
(1)当k 时,方程有实数根;
(2)当k 时,方程有两个相等的实数根;
(3)当k 时,方程没有实数根.
≤4
=4
>4
7.一元二次方程根与系数的关系
若一元二次方程ax2+bx+c=0(a≠0)有两个实数根x1,x2,则
x1+x2= ,x1x2=
例7. 已知α,β是方程x2+2x-5=0的两根,则
(1)α+β= ;
(2)αβ= .
-2
-5
8.一元二次方程的应用
(1)变化率问题
①设a为基础量,m为平均增长率,n为增长次数,b为增长后的量,则b=a(1+m)n;
②设a为基础量,p为平均下降率,q为下降次数,c为下降后的量,则c=
.
a(1-p)q
(2)传播问题
设a为传播源数,m为每个传播源每轮传播的数量,n为传播的轮次,b为传播后的总数量.
分析如下:
a a+am a+am+m
(a+am)=a(1+m)2
总结:b= .
a(1+m)n
(5)面积问题
注:图形经过移动,它的面积大小不会改变.
设图①、图②、图③中大矩形的长为a,宽为b,阴影部分的宽为x;图④是由一面墙和篱笆围成,设篱笆总长度为m,平行于墙的一边长为y.
①S空白=
②S空白=
③S空白=
④S空白=
(a-2x)(b-2x)
(a-x)(b-x)
(a-x)(b-x)
(6)动点问题:
①一般设运动时间为t,表示出动点运动的距离;
②通过几何性质表示出其他所需的线段;
③根据面积、勾股定理等数量关系建立方程;
④通过解方程找出动点的位置或其他相关信息
例8.(1)某厂今年一月份的总产量为500 t,三月份的总产量为720 t,平均每月增长率是x,则可列方程为 ( )
A. 500(1+2x)=720
B. 720(1+x)2=500
C. 500(1+x2)=720
D. 500(1+x)2=720
D
(2)有一人患流感,经过两轮传染后共有121人患了流感,求每轮传染中平均一个人传染了几个人.如果设每轮传染中平均一个人传染了x个人,那么依题意可得方程为 ( )
A. 1+x+x2=121
B. 1+x+x(1+x)=121
C. x2=121
D. 1+2x=121
B
A
(4)某商场销售一款毛衣,平均每天可售出30件,每件获利28元.受气温影响,商场决定适当降价出售.据调查,毛衣单价每降低1元,每天可多售出3件.要使每天获利1 080元,每件应降价多少元?设每件降价x元,则可列方程为 .
(28-x)(30+3x)=1 080
(5)如图2-7-3,在长为30 m,宽为20 m的长方形田地中开辟三条入口宽度相等的道路,已知剩余田地的面积为468 m2,求道路的宽度.设道路的宽度为x m,则可列方程为 .
(30-2x)(20-x)=468
广东中考
1. (2024·广东题13,3分,根的判别式)若关于x的一元二次方程x2+2x+c=0有两个相等的实数根,则c= .
2. (2022·广东题14,3分,一元二次方程的解)若x=1是方程x2-2x+a=0的根,则a= .
3. (2021·广东题14,4分,一元二次方程根与系数的关系)若一元二次方程x2+bx+c=0(b,c为常数)的两根x1,x2满足-3
1
x2-2=0(答案不唯一)
高分击破
温馨提示:此类考题可能见于广东省中考数学试卷的第17题,分值一般为7分,答题时要注意书写格式,分步书写,慢做会求全对,评卷老师是分步给分的哦!
【典型考点】一元二次方程的应用
2. (2024·深圳模拟)某品牌画册每本成本为40元,当售价为60元时,平均每天的销售量为100本. 为了吸引消费者,商家决定采取降价措施. 经试销统计发现,当画册售价每降低1元时,平均每天就能多售出10本. 设这种画册每本降价x元.
(1)平均每天的销售量为 本;(用含x的代数式表示)
(100+10x)
(2)商家想要使这种画册的销售利润平均每天达到2 240元,且要求每本售价不低于55元,求每本画册应降价多少元.
解:(2)由题意,得(60-40-x)(100+10x)=2 240.
整理,得x2-10x+24=0.
解得x1=4,x2=6.
∵要求每本售价不低于55元,∴60-x≥55,即x≤5.∴x=4.
答:每本画册应降价4元.
【典型错例】用配方法时,配方前没有把二次项系数化为1而导致配方错误
3. 用配方法解方程:2x2-8x+3=0.
【生长式训练】知识生长→变式创新
4. (中考创新,原创题)已知a,b是关于x的一元二次方程x2-18x+3m=0(m>0)的两个实数根.
知识种子:基本概念
(1)m的取值范围是 ;
0
(3)若(a-1)(b-1)=13,求m的值;
解:由题意,得a+b=18,ab=3m.
∵(a-1)(b-1)=ab-(a+b)+1=13,
∴3m-18+1=13. 解得m=10.
∴m的值为10.
种子成树:综合创新
(4)为了便于劳动课程的开展,学校打算建一个矩形生态园ABCD(如图2-7-5),生态园一面靠墙(墙长9 m),另外三面用篱笆围成. 已知当AD的长为a m,CD的长为b m时,生态园的面积为80 m2,求此时AD的长.
解:由题意,得a+b=18.
∴b=18-a.
∵四边形ABCD是矩形,
∴BC=AD=a m,AB=CD=(18-a) m.
∵生态园的面积为80 m2,
∴a(18-a)=80. 解得a1=8,a2=10.
当a=8时,AB=18-a=10>9,不合题意,舍去;
当a=10时,AB=18-a=8<9,符合题意.
答:此时AD的长为10 m.
中考演练
(限时15分钟)
B
A
B
4. (2024·牡丹江)一种药品原价每盒48元,经过两次降价后每盒27元,两次降价的百分率相同,则每次降价的百分率为 ( )
A. 20% B. 22% C. 25% D. 28%
C
5. (2024·通辽)如图2-7-6,小程的爸爸用一段10 m长的铁丝网围成一个一边靠墙(墙长5.5 m)的矩形鸭舍,其面积为15 m2,在鸭舍侧面中间位置留一个1 m宽的门(由其他材料制成),则BC长为 ( )
A. 5 m或6 m
B. 2.5 m或3 m
C. 5 m
D. 3 m
C
二、填空题
6. (2024·深圳)一元二次方程x2-3x+a=0的一个解为x=1,则a= .
7. (2024·新疆)关于x的一元二次方程x2+3x+k=0有两个不相等的实数根,
则k的取值范围为 .
8. (2024·烟台)若一元二次方程2x2-4x-1=0的两根为m,n,则3m2-4m+n2的值为 .
2
6
10. (2023·郴州)随旅游旺季的到来,某景区游客人数逐月增加,2月份游客人数为1.6万人,4月份游客人数为2.5万人.
(1)求这两个月中该景区游客人数的月平均增长率;
解:(1)设这两个月中该景区游客人数的月平均增长率为x.
由题意,得1.6(1+x)2=2.5.
解得x1=0.25=25%,x2=-2.25(不合题意,舍去).
答:这两个月中该景区游客人数的月平均增长率为25%.
(2)预计5月份该景区游客人数会继续增长,但增长率不会超过前两个月的月平均增长率. 已知该景区5月1日至5月21日已接待游客2.125万人,则5月份后10天日均接待游客人数最多是多少万人?
(2)设5月份后10天日均接待游客人数是a万人.
由题意,得2.125+10a≤2.5×(1+25%).
解得a≤0.1.
答:5月份后10天日均接待游客人数最多是0.1万人.
命题趋势
(限时 5 分钟)
(原创题)某商店以每件45元的价格购进某款学习软件,以每件68元的价格出售,经统计,5月份的销售量为256件,7月份的销售量为400件.
(1)求该款学习软件6,7月份销售量的月平均增长率;
解:(1)设该款学习软件6,7月份销售量的月平均增长率为x.
由题意,得256(1+x)2=400.
解得x1=0.25=25%,x2=-2.25(不合题意,舍去).
答:该款学习软件6,7月份销售量的月平均增长率为25%.
(2)经市场预测,8月份的销售量将与7月份持平,为减少库存,商店决定降价促销. 调查发现,该款学习软件每降价1元,月销售量就会增加20件. 当该款学习软件降价多少元时,月销售利润达到8 400元?
(2)设该款学习软件降价m元.
由题意,得(68-45-m)(400+20m)=8 400.
整理,得m2-3m-40=0.
解得m1=8,m2=-5(不合题意,舍去).
答:当该款学习软件降价8元时,月销售利润达到8 400元.
命题解读:根据最新课程标准和近三年中考命题动向,预测2025年中考命题方向可能注重考查对一元二次方程基本概念的理解,如根的判别式、方程的解、根与系数的关系等;强调运用公式法、配方法等解一元二次方程;注重一元二次方程在实际问题中的应用,如利润、增长率等问题;还可能会与函数、几何等知识点综合考查.
同课章节目录
