中考数学复习知识梳理第二章方程(组)与不等式(组)第5课时一次方程(组)及其应用课件(共39张PPT)
文档属性
| 名称 | 中考数学复习知识梳理第二章方程(组)与不等式(组)第5课时一次方程(组)及其应用课件(共39张PPT) |  | |
| 格式 | ppt | ||
| 文件大小 | 4.9MB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 通用版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2025-05-31 09:52:02 | ||
图片预览











文档简介
(共39张PPT)
第二章 方程(组)与不等式(组)
第5课时 一次方程(组)及其应用
课前循环练
(限时5分钟)
D
D
A
-2
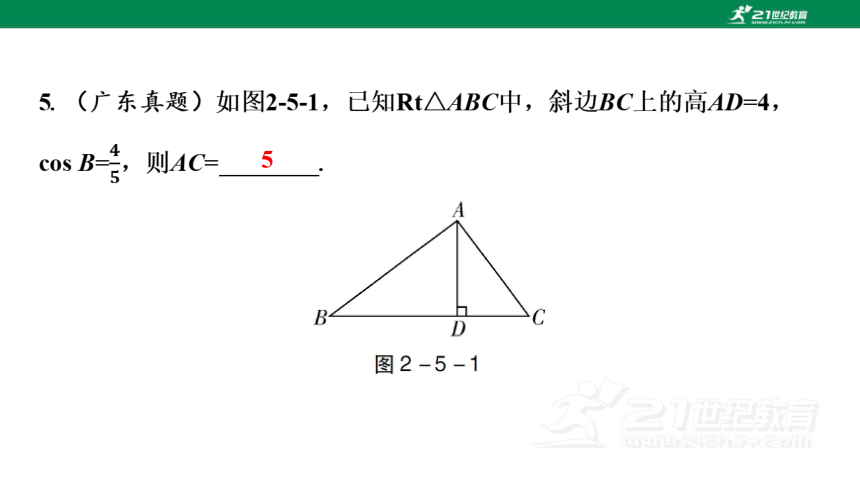
5
①能根据现实情境理解方程的意义,能针对具体问题列出方程;理解方程解的意义,经历估计方程解的过程.
②掌握等式的基本性质;能解一元一次方程和可化为一元一次方程的分式方程.
③掌握消元法,能解二元一次方程组.
④*能解简单的三元一次方程组.
课标要求
对接教材 人教:七上第三章 一元一次方程;七下第八章 二元一次方程组
北师:七上第五章 一元一次方程;八上第五章 二元一次方程组
考点梳理
考点复习
1.一元一次方程
(1)含有 的等式叫做方程.
(2)在一个方程中,只含有 未知数,未知数的次数都是 ,等号两边都是 ,这样的方程叫做一元一次方程.
(3)使方程左、右两边的值相等的 的值,叫做方程的解
未知数
一个
1
整式
未知数
①②
b±c
bc
B
3.一元一次方程的解法
(1)依据:等式的基本性质.
(2)一般步骤:①去分母;②去括号;③移项;④合并同类项;⑤未知数的系数化为1
4.二元一次方程组
(1)含有 未知数,并且所含未知数的项的次数都是 的方程叫做二元一次方程.
(2)共含有两个未知数的两个一次方程所组成的一组方程,叫做二元一次方程组
两个
1
③④
5.二元一次方程组的解法
(1)代入消元法:把二元一次方程组中一个方程的一个未知数用含____
未知数的式子表示出来,再 另一个方程,实现消元,进而求得这个二元一次方程组的解的方法叫做代入消元法,简称 .
(2)加减消元法:当二元一次方程组的两个方程中同一个未知数的系数
或 时,把这两个方程的两边分别 或 ,就能消去这个未知数,得到一个一元一次方程,这种方法叫做加减消元法,简称
另一个
代入
代入法
相反
相等
相加
相减
加减法
例6. 港珠澳大桥是世界上最长的跨海大桥,它由桥梁和隧道两部分组成,桥梁和隧道全长共55 km,其中桥梁长度比隧道长度的9倍少4 km.求港珠澳大桥的桥梁长度和隧道长度.
广东中考
高分击破
温馨提示:此类考题常见于广东省中考数学试卷的第17题,分值一般为7分,答题时要注意书写格式,分步书写,慢做会求全对,评卷老师是分步给分的哦!
【典型考点】一元一次方程(或二元一次方程组)的应用
2. (2024·长春,数学文化)《九章算术》是我国第一部自成体系的数学专著,其中“盈不足术”记载:今有共买金,人出四百,盈三千四百;人出三百,盈一百. 问人数、金价各几何?译文:今有人合伙买金,每人出400钱,剩余3 400钱;每人出300钱,剩余100钱. 问合伙人数和金价各是多少?请解答这个问题.
【典型错例】去分母时,分子是多项式没添括号,常数项漏乘最简公分母
1
7
生长变式:方程变式
(3)对于实数x,y,定义新运算:x*y=ax+by+c(其中a,b,c是常数),等式右边是通常的加法和乘法运算. 已知3*5=15,4*7=28,求1*1的值;
种子成树:综合创新
(4)某班级组织活动购买小奖品,买20支铅笔、3块橡皮、2本日记本共需32元,买39支铅笔、5块橡皮、3本日记本共需58元,则购买5支铅笔、5块橡皮、5本日记本共需多少元?
中考演练
(限时15分钟)
一、选择题
1. (2023·海南)若代数式x+2的值为7,则x等于 ( )
A. 9 B. -9 C. 5 D. -5
2. (2023·永州)关于x的一元一次方程2x+m=5的解为x=1,则m的值为 ( )
A. 3 B. -3 C. 7 D. -7
C
A
D
A
C
2
8. (2024·贵州,数学文化)在元朝朱世杰所著的《算学启蒙》中,记载了一道题,大意是:快马每天行240里,慢马每天行150里,慢马先行12天,则快马追上慢马需要的天数是 .
20天
三、解答题
9. (2024·山西)当下电子产品更新换代速度加快,废旧智能手机数量不断增加. 科学处理废旧智能手机,既可减少环境污染,还可回收其中的可利用资源. 据研究,从每吨废旧智能手机中能提炼出的白银比黄金多760 g. 已知从2.5 t废旧智能手机中提炼出的黄金,与从0.6 t废旧智能手机中提炼出的白银克数相等. 求从每吨废旧智能手机中能提炼出黄金与白银各多少克.
10. (数学文化)民间刺绣历史悠久,而且题材广泛,内容丰富,具有反映风土人情的特色. “五一”期间,小颖去博物馆游览,她决定买一些刺绣工艺品送给亲戚朋友. 现有甲、乙两种刺绣工艺品,已知2件甲种刺绣工艺品和3件乙种刺绣工艺品共需90元,3件甲种刺绣工艺品和5件乙种刺绣工艺品共需145元.
(1)求甲、乙两种刺绣工艺品的单价各是多少元;
(2)若小颖决定用270元购买15件这两种刺绣工艺品,则她最多可购买多少件乙种刺绣工艺品?
(2)设小颖可购买m件乙种刺绣工艺品,则购买(15-m)件甲种刺绣工艺品.
由题意,得20m+15(15-m)≤270. 解得m≤9.
答:小颖最多可购买9件乙种刺绣工艺品.
命题趋势
(限时 5 分钟)
(2023·宜昌,数学文化)为纪念爱国诗人屈原,人们有了端午节吃粽子的习俗. 某顾客端午节前在超市购买豆沙粽10个,肉粽12个,共付款136元,已知肉粽单价是豆沙粽的2倍.
(1)求豆沙粽和肉粽的单价;
解:(1)设豆沙粽的单价为x元,则肉粽的单价为2x元.
由题意,得10x+12×2x=136. 解得x=4. 则2x=8.
答:豆沙粽的单价为4元,肉粽的单价为8元.
(2)超市为了促销,购买粽子达20个及以上时实行优惠,下表列出了小欢妈妈、小乐妈妈的购买数量和付款金额:
①根据上表,求豆沙粽和肉粽优惠后的单价;
豆沙粽数量/个 肉粽数量/个 付款金额/元
小欢妈妈 20 30 270
小乐妈妈 30 20 230
②为进一步提升粽子的销量,超市将两种粽子打包成A,B两种包装销售,每包都是40个粽子(包装成本忽略不计),每包的销售价格按其中每个粽子优惠后的单价合计. A,B两种包装中分别有m个豆沙粽,m个肉粽,A包装中的豆沙粽数量不超过肉粽的一半. 端午节当天统计发现,A,B两种包装的销量分别为(80-4m)包,(4m+8)包,A,B两种包装的销售总额为17 280元. 求m的值.
命题解读:根据最新课程标准和近三年中考命题动向,预测2025年中考命题方向可能注重考查一次方程(组)的解法;强调一次方程(组)的实际应用,可能会结合实际生活情境或数学文化背景出题;注重与其他数学知识的结合,可能会结合函数、几何、不等式等知识综合考查.
第二章 方程(组)与不等式(组)
第5课时 一次方程(组)及其应用
课前循环练
(限时5分钟)
D
D
A
-2
5
①能根据现实情境理解方程的意义,能针对具体问题列出方程;理解方程解的意义,经历估计方程解的过程.
②掌握等式的基本性质;能解一元一次方程和可化为一元一次方程的分式方程.
③掌握消元法,能解二元一次方程组.
④*能解简单的三元一次方程组.
课标要求
对接教材 人教:七上第三章 一元一次方程;七下第八章 二元一次方程组
北师:七上第五章 一元一次方程;八上第五章 二元一次方程组
考点梳理
考点复习
1.一元一次方程
(1)含有 的等式叫做方程.
(2)在一个方程中,只含有 未知数,未知数的次数都是 ,等号两边都是 ,这样的方程叫做一元一次方程.
(3)使方程左、右两边的值相等的 的值,叫做方程的解
未知数
一个
1
整式
未知数
①②
b±c
bc
B
3.一元一次方程的解法
(1)依据:等式的基本性质.
(2)一般步骤:①去分母;②去括号;③移项;④合并同类项;⑤未知数的系数化为1
4.二元一次方程组
(1)含有 未知数,并且所含未知数的项的次数都是 的方程叫做二元一次方程.
(2)共含有两个未知数的两个一次方程所组成的一组方程,叫做二元一次方程组
两个
1
③④
5.二元一次方程组的解法
(1)代入消元法:把二元一次方程组中一个方程的一个未知数用含____
未知数的式子表示出来,再 另一个方程,实现消元,进而求得这个二元一次方程组的解的方法叫做代入消元法,简称 .
(2)加减消元法:当二元一次方程组的两个方程中同一个未知数的系数
或 时,把这两个方程的两边分别 或 ,就能消去这个未知数,得到一个一元一次方程,这种方法叫做加减消元法,简称
另一个
代入
代入法
相反
相等
相加
相减
加减法
例6. 港珠澳大桥是世界上最长的跨海大桥,它由桥梁和隧道两部分组成,桥梁和隧道全长共55 km,其中桥梁长度比隧道长度的9倍少4 km.求港珠澳大桥的桥梁长度和隧道长度.
广东中考
高分击破
温馨提示:此类考题常见于广东省中考数学试卷的第17题,分值一般为7分,答题时要注意书写格式,分步书写,慢做会求全对,评卷老师是分步给分的哦!
【典型考点】一元一次方程(或二元一次方程组)的应用
2. (2024·长春,数学文化)《九章算术》是我国第一部自成体系的数学专著,其中“盈不足术”记载:今有共买金,人出四百,盈三千四百;人出三百,盈一百. 问人数、金价各几何?译文:今有人合伙买金,每人出400钱,剩余3 400钱;每人出300钱,剩余100钱. 问合伙人数和金价各是多少?请解答这个问题.
【典型错例】去分母时,分子是多项式没添括号,常数项漏乘最简公分母
1
7
生长变式:方程变式
(3)对于实数x,y,定义新运算:x*y=ax+by+c(其中a,b,c是常数),等式右边是通常的加法和乘法运算. 已知3*5=15,4*7=28,求1*1的值;
种子成树:综合创新
(4)某班级组织活动购买小奖品,买20支铅笔、3块橡皮、2本日记本共需32元,买39支铅笔、5块橡皮、3本日记本共需58元,则购买5支铅笔、5块橡皮、5本日记本共需多少元?
中考演练
(限时15分钟)
一、选择题
1. (2023·海南)若代数式x+2的值为7,则x等于 ( )
A. 9 B. -9 C. 5 D. -5
2. (2023·永州)关于x的一元一次方程2x+m=5的解为x=1,则m的值为 ( )
A. 3 B. -3 C. 7 D. -7
C
A
D
A
C
2
8. (2024·贵州,数学文化)在元朝朱世杰所著的《算学启蒙》中,记载了一道题,大意是:快马每天行240里,慢马每天行150里,慢马先行12天,则快马追上慢马需要的天数是 .
20天
三、解答题
9. (2024·山西)当下电子产品更新换代速度加快,废旧智能手机数量不断增加. 科学处理废旧智能手机,既可减少环境污染,还可回收其中的可利用资源. 据研究,从每吨废旧智能手机中能提炼出的白银比黄金多760 g. 已知从2.5 t废旧智能手机中提炼出的黄金,与从0.6 t废旧智能手机中提炼出的白银克数相等. 求从每吨废旧智能手机中能提炼出黄金与白银各多少克.
10. (数学文化)民间刺绣历史悠久,而且题材广泛,内容丰富,具有反映风土人情的特色. “五一”期间,小颖去博物馆游览,她决定买一些刺绣工艺品送给亲戚朋友. 现有甲、乙两种刺绣工艺品,已知2件甲种刺绣工艺品和3件乙种刺绣工艺品共需90元,3件甲种刺绣工艺品和5件乙种刺绣工艺品共需145元.
(1)求甲、乙两种刺绣工艺品的单价各是多少元;
(2)若小颖决定用270元购买15件这两种刺绣工艺品,则她最多可购买多少件乙种刺绣工艺品?
(2)设小颖可购买m件乙种刺绣工艺品,则购买(15-m)件甲种刺绣工艺品.
由题意,得20m+15(15-m)≤270. 解得m≤9.
答:小颖最多可购买9件乙种刺绣工艺品.
命题趋势
(限时 5 分钟)
(2023·宜昌,数学文化)为纪念爱国诗人屈原,人们有了端午节吃粽子的习俗. 某顾客端午节前在超市购买豆沙粽10个,肉粽12个,共付款136元,已知肉粽单价是豆沙粽的2倍.
(1)求豆沙粽和肉粽的单价;
解:(1)设豆沙粽的单价为x元,则肉粽的单价为2x元.
由题意,得10x+12×2x=136. 解得x=4. 则2x=8.
答:豆沙粽的单价为4元,肉粽的单价为8元.
(2)超市为了促销,购买粽子达20个及以上时实行优惠,下表列出了小欢妈妈、小乐妈妈的购买数量和付款金额:
①根据上表,求豆沙粽和肉粽优惠后的单价;
豆沙粽数量/个 肉粽数量/个 付款金额/元
小欢妈妈 20 30 270
小乐妈妈 30 20 230
②为进一步提升粽子的销量,超市将两种粽子打包成A,B两种包装销售,每包都是40个粽子(包装成本忽略不计),每包的销售价格按其中每个粽子优惠后的单价合计. A,B两种包装中分别有m个豆沙粽,m个肉粽,A包装中的豆沙粽数量不超过肉粽的一半. 端午节当天统计发现,A,B两种包装的销量分别为(80-4m)包,(4m+8)包,A,B两种包装的销售总额为17 280元. 求m的值.
命题解读:根据最新课程标准和近三年中考命题动向,预测2025年中考命题方向可能注重考查一次方程(组)的解法;强调一次方程(组)的实际应用,可能会结合实际生活情境或数学文化背景出题;注重与其他数学知识的结合,可能会结合函数、几何、不等式等知识综合考查.
同课章节目录
