中考数学复习知识梳理第三章函数第12课时二次函数课件(共54张PPT)
文档属性
| 名称 | 中考数学复习知识梳理第三章函数第12课时二次函数课件(共54张PPT) |  | |
| 格式 | ppt | ||
| 文件大小 | 6.4MB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 通用版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2025-05-31 09:47:57 | ||
图片预览










文档简介
(共54张PPT)
第三章 函 数
第12课时 二 次 函 数
课前循环练
(限时5分钟)
1. (广东真题)一组数据2,6,5,2,4,则这组数据的中位数是( )
A. 2 B. 4 C. 5 D. 6
2. (广东真题)到三角形三条边的距离都相等的点是这个三角形的( )
A. 三条中线的交点 B. 三条高的交点
C. 三条边的垂直平分线的交点 D. 三条角平分线的交点
B
D
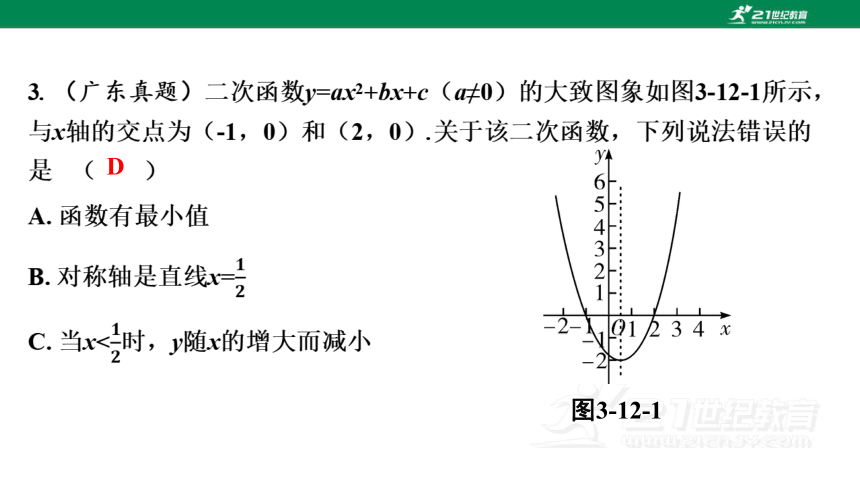
图3-12-1
D
50°
①通过对实际问题的分析,体会二次函数的意义.
②能画二次函数的图象,通过图象了解二次函数的性质,知道二次函数系数与图象形状和对称轴的关系.
③会求二次函数的最大值或最小值,并能确定相应自变量的值,能解决相应的实际问题.
④知道二次函数和一元二次方程之间的关系,会利用二次函数的图象求一元二次方程的近似解.
课标要求
对接教材 人教:九上第二十二章 二次函数
北师:九下第二章 二次函数
考点梳理
考点复习
1.二次函数的概念
一般地,形如y=ax2+bx+c(a,b,c为常数,a≠0)的函数,叫做二次函数
②④⑤
2.二次函数y=ax2+bx+c(a≠0)的图象与性质
函数 二次函数y=ax2+bx+c(a,b,c是常数,a≠0)
对称轴
顶点坐标 _____________________
图象 a>0 a<0
开口方向 向上 向下
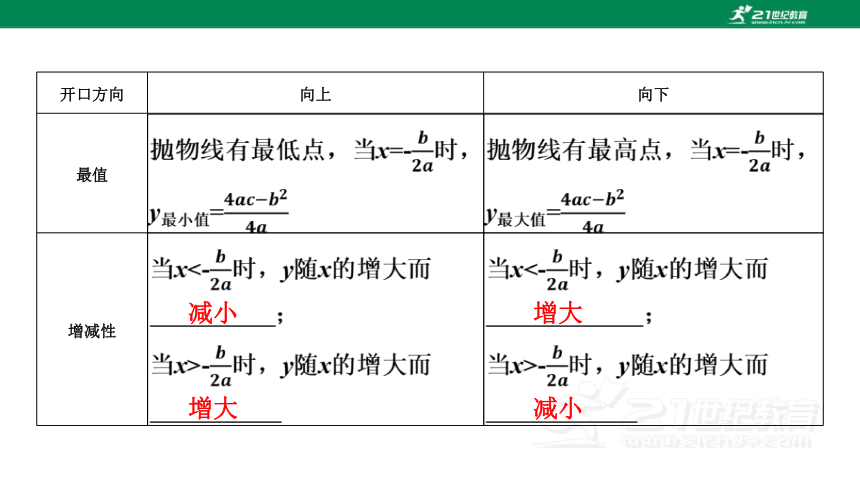
最值
增减性
减小
增大
增大
减小
例2.已知抛物线y=x2-2x-8.
(1)开口方向是 ;
(2)对称轴是 ,顶点坐标是 ;
(3)与x轴的交点坐标是 ;
(4)当x 时,y随x的增大而增大,当x 时,y随x的增大而减小;
(5)当x= 时,y有最 值为 .
向上
直线x=1
(1,-9)
(4,0),(-2,0)
>1
<1
1
小
-9
3.抛物线y=a(x-h)2+k与y=ax2的关系
(1)抛物线y=a(x-h)2+k与y=ax2的形状相同,位置不同,y=a(x-h)2+k是由y=ax2通过平移得到的,平移后的顶点坐标为 .
(2)y=ax2的图象
y=a(x-h)2的图象
y=a(x-h)2+k的图象
(h,k)
右
左
上
下
例3. 将抛物线y=3x2向左平移2个单位长度,再向下平移1个单位长度,所得到的抛物线解析式为 .(写成一般式)
y=3x2+12x+11
4.确定二次函数的解析式
(1)若已知抛物线上三个点的坐标,可设解析式为一般式:__________
;
(2)若已知抛物线的顶点坐标或对称轴或最值,可设解析式为顶点式:
;
(3)若已知抛物线与x轴两个交点的横坐标,可设解析式为两点式:___
y=ax2+bx+c(a≠0)
y=a(x-h)2+k(a≠0)
y=a(x-x1)(x-x2)(a≠0)
例4. 在直角坐标系中,点A,B,C的坐标分别为(-1,0),(3,0),(0,3).求过A,B,C三点的抛物线的解析式.
解:设抛物线的解析式为y=a(x+1)(x-3).
将点(0,3)代入上式,得-3a=3.
解得a=-1.
∴抛物线的解析式为y=-(x+1)(x-3)=-x2+2x+3.
5.二次函数的图象与各项系数之间的关系
代数式 作用 字母符号 图象的特征
a 决定开口方向 a>0 开口
a<0 开口
c 决定抛物线与y轴的交点坐标(0,c) c>0 交点在x轴上方
c=0 抛物线经过
c<0 交点在x轴
向上
向下
原点
下方
代数式 作用 字母符号 图象的特征
ab>0 对称轴在y轴左侧
b=0 对称轴是
ab<0 对称轴在y轴
b2-4ac 决定抛物线与x轴的交点个数 b2-4ac>0 与x轴有两个交点
b2-4ac=0 与x轴有 交点
b2-4ac<0 与x轴 交点
y轴
右侧
一个
没有
例5. 如图3-12-2,二次函数y=ax2+bx+c的图象经过点A(-3,0),其对称轴为直线x=-1.有下列结论:①abc<0;②a+b+c<0;③2a-b=0;④4ac-b2>0;⑤若P(-5,y1),Q(m,y2)是抛物线上两点,且y1>y2,则实数m的取值范围是-5A. 1个
B. 2个
C. 3个
D. 4个
图3-12-2
C
6.二次函数与一元二次方程、不等式的关系
(1)二次函数与一元二次方程的关系
Δ=b2-4ac 方程ax2+bx+c=0
的实数根情况 抛物线y=ax2+bx+c
与x轴的交点情况
Δ>0 两个不相等的实数根 两个交点
Δ=0
Δ<0
方程ax2+bx+c=0的根是抛物线y=ax2+bx+c与x轴的交点的横坐标
两个相等的实数根
一个交点
没有实数根
没有交点
6.(2)二次函数与不等式的关系
①不等式ax2+bx+c>0的解集 抛物线y=ax2+bx+c的图象位于x轴上方对应的点的横坐标的取值范围;
②不等式ax2+bx+c<0的解集 抛物线y=ax2+bx+c的图象位于x轴下方对应的点的横坐标的取值范围
例6.二次函数y=ax2+bx+c(a≠0)的图象如图3-12-3所示,根据图象解答下列问题:
(1)写出方程ax2+bx+c=0的两个根: ;
(2)写出不等式ax2+bx+c>0的解集: ;
(3)写出y随x的增大而减小的自变量x的取值范围: ;
(4)若方程ax2+bx+c=k有两个不相等的实数根,根据图象写出k的取值范围: .
图3-12-3
x1=1,x2=3
1x>2
k<2
7.二次函数的应用
运用二次函数解决实际问题,首先要用二次函数表示问题中变量之间的关系,然后利用二次函数的图象和性质求解,从而获得实际问题的答案
例7. 某超市购进一批单价为8元的生活用品,如果按每件9元出售,那么每天可销售20件.经调查发现,这种生活用品的销售单价每提高1元,其销售量相应减少4件,那么将销售价定为 元时,才能使每天所获销售利润最大.
11
广东中考
1. (2024·广东题8,3分,二次函数的图象与性质)若点(0,y1),(1,y2),(2,y3)都在二次函数y=x2的图象上,则 ( )
A. y3>y2>y1 B. y2>y1>y3
C. y1>y3>y2 D. y3>y1>y2
A
2. (2023·广东题10,3分,二次函数图象上点的坐标特征)如图3-12-4,抛物线y=ax2+c经过正方形OABC的三个顶点A,B,C,点B在y轴上,则ac的值为 ( )
A. -1 B. -2
C. -3 D. -4
图3-12-4
B
A
4. (2021·广东题12,4分,二次函数图象与几何变换)把抛物线y=2x2+1向左平移1个单位长度,再向下平移3个单位长度,得到的抛物线的解析式为 .
y=2(x+1)2-2或y=2x2+4x
5. (2024·广东题20,9分,二次函数的应用)广东省全力实施“百县千镇万村高质量发展工程”,2023年农产品进出口总额居全国首位,其中荔枝鲜果远销欧美. 某果商以每吨2万元的价格收购早熟荔枝,销往国外.若按每吨5万元出售,平均每天可售出100 t. 市场调查反映:如果每吨降价1万元,每天销售量相应增加50 t. 该果商如何定价才能使每天的“利润”或“销售收入”最大?并求出其最大值. (题中“元”为人民币)
解法一:(求利润)设该果商定价为每吨x万元,每天的利润为w万元.
由题意,得w=(x-2)[100+50(5-x)]=-50(x-4.5)2+312.5.
∵-50<0,∴当x=4.5时,w有最大值,最大值为312.5.
答:该果商定价为每吨4.5万元时,每天的利润最大,最大值为312.5万元.
解法二:(求销售收入)设该果商定价为每吨x万元,每天的销售收入为w万元.
由题意,得w=x[100+50(5-x)]=-50(x-3.5)2+612.5.
∵-50<0,∴当x=3.5时,w有最大值,最大值为612.5.
答:该果商定价为每吨3.5万元时,每天的销售收入最大,最大值为612.5万元.
高分击破
【典型考点】二次函数综合题 得分点分析
1. (2022·广东)如图3-12-5,抛物线y=x2+bx+c(b,c是常数)的顶点为C,与x轴交于A,B两点,A(1,0),AB=4,点P为线段AB上的动点,过点P作PQ∥BC交AC于点Q.
(1)求该抛物线的解析式;
(2)求△CPQ面积的最大值,并求此时点P的坐标.
温馨提示:此类考题常见于广东省中考数学试卷的第22题,分值一般为13分,答题时要注意书写格式,分步书写,慢做会求全对,评卷老师是分步给分的哦!
【典型考点】二次函数的应用
2. (2024·烟台)每年5月的第三个星期日为全国助残日,今年的主题是“科技助残,共享美好生活”. 康宁公司新研发了一批便携式轮椅,计划在该月销售. 根据市场调查,每辆轮椅盈利200元时,每天可售出60辆;单价每降低10元,每天可多售出4辆. 公司决定在成本不变的情况下降价销售,但每辆轮椅的利润不低于180元. 设每辆轮椅降价x元,每天的销售利润为y元.
(1)求y与x的函数关系式;每辆轮椅降价多少元时,每天的销售利润最大?最大利润为多少元?
(2)全国助残日当天,公司共获得销售利润12 160元,请问这天售出了多少辆轮椅?
【典型错例】在二次函数的应用中,忽略自变量的取值范围
3. 用一段长为24 m的篱笆围成一个一边靠墙的矩形养鸡场,若墙长8 m,则这个养鸡场的最大面积为 ( )
A. 36 m2
B. 64 m2
C. 72 m2
D. 96 m2
B
图3-12-7
(-2,0)
(4,0)
(0,-4)
种子生长:等角问题
(2)抛物线上是否存在点M,使∠BCM=∠ABC?若存在,求出点M的坐标;若不存在,请说明理由;
图3-12-7
答图3-12-1
生长变式:角度变式
(3)在第一象限内的抛物线上是否存在点N,使∠BCN=15°?若存在,求出点N的坐标;若不存在,请说明理由;
解:存在.
如答图3-12-2,设点N为第一象限内的抛物线上的一点,且∠BCN=15°,CN与x轴交于点D.
答图3-12-2
图3-12-7
答图3-12-2
种子成树:综合创新
(4)如图3-12-8,若D是抛物线第二象限上一动点,过点D作DF⊥x轴于点F,过点A,B,D的圆与DF交于点E,求△ABE的面积.
图3-12-8
答图3-12-3
中考演练
(限时15分钟)
一、选择题
1. (2023·兰州)已知二次函数y=-3(x-2)2-3,下列说法正确的是
( )
A. 对称轴为直线x=-2 B. 顶点坐标为(2,3)
C. 函数的最大值是-3 D. 函数的最小值是-3
C
3. (2024·天津,跨学科融合)从地面竖直向上抛出一小球,小球的高度h(m)与小球的运动时间t(s)之间的关系式是h=30t-5t2(0≤t≤6). 有下列结论:①小球从抛出到落地需要6 s;②小球运动中的高度可以是30 m;③小球运动2 s时的高度小于运动5 s时的高度. 其中,正确结论的个数是 ( )
A. 0 B. 1 C. 2 D. 3
C
2. (2024·包头)将抛物线y=x2+2x向下平移2个单位长度后,所得新抛物线的顶点式为 ( )
A. y=(x+1)2-3 B. y=(x+1)2-2
C. y=(x-1)2-3 D. y=(x-1)2-2
A
4. (2024·贵州)如图3-12-9,二次函数y=ax2+bx+c的部分图象与x轴的一个交点的横坐标是-3,顶点坐标为(-1,4),则下列说法正确的是 ( )
A. 二次函数图象的对称轴是直线x=1
B. 二次函数图象与x轴的另一个交点的横坐标是2
C. 当x<-1时,y随x的增大而减小
D. 二次函数图象与y轴的交点的纵坐标是3
图3-12-9
D
图3-12-10
B
二、填空题
6. (2024·滨州)将抛物线y=-x2先向右平移1个单位长度,再向上平移2个单位长度,则平移后抛物线的顶点坐标为 .
7. (2024·宁夏)若二次函数y=2x2-x+m的图象与x轴有交点,则m的取值范围是 .
(1,2)
8. (2024·辽宁)如图3-12-11,在平面直角坐标系中,抛物线y=ax2+bx+3与x轴相交于点A,B,点B的坐标为(3,0),若点C(2,3)在抛物线上,则AB的长为 .
图3-12-11
4
三、解答题
9. (2023·宿迁)某商场销售A,B两种商品,每件进价均为20元. 调查发现,如果售出A种20件,B种10件,销售总额为840元;如果售出A种10件,B种15件,销售总额为660元.
(1)求A,B两种商品的销售单价;
(2)经市场调研,A种商品按原售价销售,可售出40件,原售价每降价1元,销售量可增加10件;B种商品的售价不变,A种的商品售价不低于B种商品的售价. 设A种商品降价m元,如果A,B两种商品的销售量相同,那么当m取何值时,商场销售A,B两种商品可获得总利润最大?最大利润是多少?
(2)∵A种的商品售价不低于B种商品的售价,∴30-m≥24. 解得m≤6.
设总利润为w元.
由题意,得w=(30-m-20)(40+10m)+(24-20)(40+10m)
=-10(m-5)2+810.
∵-10<0,且m≤6,
∴当m=5时,w有最大值,最大值为810.
答:当m=5时,商场销售A,B两种商品可获得总利润最大,最大利润是810元.
图3-12-12
(2)点P是抛物线在第四象限图象上的任意一点,当△BCP的面积最大时,求BC边上的高PN的值.
图3-12-12
答图3-12-4
命题趋势
( 限时 5 分钟)
(综合运用)【问题背景】
如图3-12-13,抛物线y=-x2+bx+c交x轴于点A,交y轴于点B,已知经过点A,B的直线的表达式为y=x+3,点P(m,0)是线段AO上的一个动点,其中
-3图3-12-13
【构建联系】
(1)求抛物线的函数表达式;
(2)如图3-12-13①,作EF∥x轴,交直线AB于点F,四边形DEFG为矩形,当矩形DEFG的周长为9时,求m的值;
图3-12-13
(3)如图3-12-13②,作DE的中垂线MQ交AB于点M,交DE于点Q,在MQ延长线上取点N,使QN=4MQ,求点N到y轴的最远距离.
图3-12-13
图3-12-13
命题解读:根据最新课程标准和近三年中考命题动向,预测2025年中考命题方向可能注重考查二次函数的基本概念、图象与性质,如对称轴、顶点坐标、最值、图象的平移等;强调二次函数与其他数学知识的综合运用,可能与方程、不等式、其他函数、几何图形等综合考查;注重与实际问题的紧密结合,可能会出现经济、科技、生活等多个领域的实际情境.
第三章 函 数
第12课时 二 次 函 数
课前循环练
(限时5分钟)
1. (广东真题)一组数据2,6,5,2,4,则这组数据的中位数是( )
A. 2 B. 4 C. 5 D. 6
2. (广东真题)到三角形三条边的距离都相等的点是这个三角形的( )
A. 三条中线的交点 B. 三条高的交点
C. 三条边的垂直平分线的交点 D. 三条角平分线的交点
B
D
图3-12-1
D
50°
①通过对实际问题的分析,体会二次函数的意义.
②能画二次函数的图象,通过图象了解二次函数的性质,知道二次函数系数与图象形状和对称轴的关系.
③会求二次函数的最大值或最小值,并能确定相应自变量的值,能解决相应的实际问题.
④知道二次函数和一元二次方程之间的关系,会利用二次函数的图象求一元二次方程的近似解.
课标要求
对接教材 人教:九上第二十二章 二次函数
北师:九下第二章 二次函数
考点梳理
考点复习
1.二次函数的概念
一般地,形如y=ax2+bx+c(a,b,c为常数,a≠0)的函数,叫做二次函数
②④⑤
2.二次函数y=ax2+bx+c(a≠0)的图象与性质
函数 二次函数y=ax2+bx+c(a,b,c是常数,a≠0)
对称轴
顶点坐标 _____________________
图象 a>0 a<0
开口方向 向上 向下
最值
增减性
减小
增大
增大
减小
例2.已知抛物线y=x2-2x-8.
(1)开口方向是 ;
(2)对称轴是 ,顶点坐标是 ;
(3)与x轴的交点坐标是 ;
(4)当x 时,y随x的增大而增大,当x 时,y随x的增大而减小;
(5)当x= 时,y有最 值为 .
向上
直线x=1
(1,-9)
(4,0),(-2,0)
>1
<1
1
小
-9
3.抛物线y=a(x-h)2+k与y=ax2的关系
(1)抛物线y=a(x-h)2+k与y=ax2的形状相同,位置不同,y=a(x-h)2+k是由y=ax2通过平移得到的,平移后的顶点坐标为 .
(2)y=ax2的图象
y=a(x-h)2的图象
y=a(x-h)2+k的图象
(h,k)
右
左
上
下
例3. 将抛物线y=3x2向左平移2个单位长度,再向下平移1个单位长度,所得到的抛物线解析式为 .(写成一般式)
y=3x2+12x+11
4.确定二次函数的解析式
(1)若已知抛物线上三个点的坐标,可设解析式为一般式:__________
;
(2)若已知抛物线的顶点坐标或对称轴或最值,可设解析式为顶点式:
;
(3)若已知抛物线与x轴两个交点的横坐标,可设解析式为两点式:___
y=ax2+bx+c(a≠0)
y=a(x-h)2+k(a≠0)
y=a(x-x1)(x-x2)(a≠0)
例4. 在直角坐标系中,点A,B,C的坐标分别为(-1,0),(3,0),(0,3).求过A,B,C三点的抛物线的解析式.
解:设抛物线的解析式为y=a(x+1)(x-3).
将点(0,3)代入上式,得-3a=3.
解得a=-1.
∴抛物线的解析式为y=-(x+1)(x-3)=-x2+2x+3.
5.二次函数的图象与各项系数之间的关系
代数式 作用 字母符号 图象的特征
a 决定开口方向 a>0 开口
a<0 开口
c 决定抛物线与y轴的交点坐标(0,c) c>0 交点在x轴上方
c=0 抛物线经过
c<0 交点在x轴
向上
向下
原点
下方
代数式 作用 字母符号 图象的特征
ab>0 对称轴在y轴左侧
b=0 对称轴是
ab<0 对称轴在y轴
b2-4ac 决定抛物线与x轴的交点个数 b2-4ac>0 与x轴有两个交点
b2-4ac=0 与x轴有 交点
b2-4ac<0 与x轴 交点
y轴
右侧
一个
没有
例5. 如图3-12-2,二次函数y=ax2+bx+c的图象经过点A(-3,0),其对称轴为直线x=-1.有下列结论:①abc<0;②a+b+c<0;③2a-b=0;④4ac-b2>0;⑤若P(-5,y1),Q(m,y2)是抛物线上两点,且y1>y2,则实数m的取值范围是-5
B. 2个
C. 3个
D. 4个
图3-12-2
C
6.二次函数与一元二次方程、不等式的关系
(1)二次函数与一元二次方程的关系
Δ=b2-4ac 方程ax2+bx+c=0
的实数根情况 抛物线y=ax2+bx+c
与x轴的交点情况
Δ>0 两个不相等的实数根 两个交点
Δ=0
Δ<0
方程ax2+bx+c=0的根是抛物线y=ax2+bx+c与x轴的交点的横坐标
两个相等的实数根
一个交点
没有实数根
没有交点
6.(2)二次函数与不等式的关系
①不等式ax2+bx+c>0的解集 抛物线y=ax2+bx+c的图象位于x轴上方对应的点的横坐标的取值范围;
②不等式ax2+bx+c<0的解集 抛物线y=ax2+bx+c的图象位于x轴下方对应的点的横坐标的取值范围
例6.二次函数y=ax2+bx+c(a≠0)的图象如图3-12-3所示,根据图象解答下列问题:
(1)写出方程ax2+bx+c=0的两个根: ;
(2)写出不等式ax2+bx+c>0的解集: ;
(3)写出y随x的增大而减小的自变量x的取值范围: ;
(4)若方程ax2+bx+c=k有两个不相等的实数根,根据图象写出k的取值范围: .
图3-12-3
x1=1,x2=3
1
k<2
7.二次函数的应用
运用二次函数解决实际问题,首先要用二次函数表示问题中变量之间的关系,然后利用二次函数的图象和性质求解,从而获得实际问题的答案
例7. 某超市购进一批单价为8元的生活用品,如果按每件9元出售,那么每天可销售20件.经调查发现,这种生活用品的销售单价每提高1元,其销售量相应减少4件,那么将销售价定为 元时,才能使每天所获销售利润最大.
11
广东中考
1. (2024·广东题8,3分,二次函数的图象与性质)若点(0,y1),(1,y2),(2,y3)都在二次函数y=x2的图象上,则 ( )
A. y3>y2>y1 B. y2>y1>y3
C. y1>y3>y2 D. y3>y1>y2
A
2. (2023·广东题10,3分,二次函数图象上点的坐标特征)如图3-12-4,抛物线y=ax2+c经过正方形OABC的三个顶点A,B,C,点B在y轴上,则ac的值为 ( )
A. -1 B. -2
C. -3 D. -4
图3-12-4
B
A
4. (2021·广东题12,4分,二次函数图象与几何变换)把抛物线y=2x2+1向左平移1个单位长度,再向下平移3个单位长度,得到的抛物线的解析式为 .
y=2(x+1)2-2或y=2x2+4x
5. (2024·广东题20,9分,二次函数的应用)广东省全力实施“百县千镇万村高质量发展工程”,2023年农产品进出口总额居全国首位,其中荔枝鲜果远销欧美. 某果商以每吨2万元的价格收购早熟荔枝,销往国外.若按每吨5万元出售,平均每天可售出100 t. 市场调查反映:如果每吨降价1万元,每天销售量相应增加50 t. 该果商如何定价才能使每天的“利润”或“销售收入”最大?并求出其最大值. (题中“元”为人民币)
解法一:(求利润)设该果商定价为每吨x万元,每天的利润为w万元.
由题意,得w=(x-2)[100+50(5-x)]=-50(x-4.5)2+312.5.
∵-50<0,∴当x=4.5时,w有最大值,最大值为312.5.
答:该果商定价为每吨4.5万元时,每天的利润最大,最大值为312.5万元.
解法二:(求销售收入)设该果商定价为每吨x万元,每天的销售收入为w万元.
由题意,得w=x[100+50(5-x)]=-50(x-3.5)2+612.5.
∵-50<0,∴当x=3.5时,w有最大值,最大值为612.5.
答:该果商定价为每吨3.5万元时,每天的销售收入最大,最大值为612.5万元.
高分击破
【典型考点】二次函数综合题 得分点分析
1. (2022·广东)如图3-12-5,抛物线y=x2+bx+c(b,c是常数)的顶点为C,与x轴交于A,B两点,A(1,0),AB=4,点P为线段AB上的动点,过点P作PQ∥BC交AC于点Q.
(1)求该抛物线的解析式;
(2)求△CPQ面积的最大值,并求此时点P的坐标.
温馨提示:此类考题常见于广东省中考数学试卷的第22题,分值一般为13分,答题时要注意书写格式,分步书写,慢做会求全对,评卷老师是分步给分的哦!
【典型考点】二次函数的应用
2. (2024·烟台)每年5月的第三个星期日为全国助残日,今年的主题是“科技助残,共享美好生活”. 康宁公司新研发了一批便携式轮椅,计划在该月销售. 根据市场调查,每辆轮椅盈利200元时,每天可售出60辆;单价每降低10元,每天可多售出4辆. 公司决定在成本不变的情况下降价销售,但每辆轮椅的利润不低于180元. 设每辆轮椅降价x元,每天的销售利润为y元.
(1)求y与x的函数关系式;每辆轮椅降价多少元时,每天的销售利润最大?最大利润为多少元?
(2)全国助残日当天,公司共获得销售利润12 160元,请问这天售出了多少辆轮椅?
【典型错例】在二次函数的应用中,忽略自变量的取值范围
3. 用一段长为24 m的篱笆围成一个一边靠墙的矩形养鸡场,若墙长8 m,则这个养鸡场的最大面积为 ( )
A. 36 m2
B. 64 m2
C. 72 m2
D. 96 m2
B
图3-12-7
(-2,0)
(4,0)
(0,-4)
种子生长:等角问题
(2)抛物线上是否存在点M,使∠BCM=∠ABC?若存在,求出点M的坐标;若不存在,请说明理由;
图3-12-7
答图3-12-1
生长变式:角度变式
(3)在第一象限内的抛物线上是否存在点N,使∠BCN=15°?若存在,求出点N的坐标;若不存在,请说明理由;
解:存在.
如答图3-12-2,设点N为第一象限内的抛物线上的一点,且∠BCN=15°,CN与x轴交于点D.
答图3-12-2
图3-12-7
答图3-12-2
种子成树:综合创新
(4)如图3-12-8,若D是抛物线第二象限上一动点,过点D作DF⊥x轴于点F,过点A,B,D的圆与DF交于点E,求△ABE的面积.
图3-12-8
答图3-12-3
中考演练
(限时15分钟)
一、选择题
1. (2023·兰州)已知二次函数y=-3(x-2)2-3,下列说法正确的是
( )
A. 对称轴为直线x=-2 B. 顶点坐标为(2,3)
C. 函数的最大值是-3 D. 函数的最小值是-3
C
3. (2024·天津,跨学科融合)从地面竖直向上抛出一小球,小球的高度h(m)与小球的运动时间t(s)之间的关系式是h=30t-5t2(0≤t≤6). 有下列结论:①小球从抛出到落地需要6 s;②小球运动中的高度可以是30 m;③小球运动2 s时的高度小于运动5 s时的高度. 其中,正确结论的个数是 ( )
A. 0 B. 1 C. 2 D. 3
C
2. (2024·包头)将抛物线y=x2+2x向下平移2个单位长度后,所得新抛物线的顶点式为 ( )
A. y=(x+1)2-3 B. y=(x+1)2-2
C. y=(x-1)2-3 D. y=(x-1)2-2
A
4. (2024·贵州)如图3-12-9,二次函数y=ax2+bx+c的部分图象与x轴的一个交点的横坐标是-3,顶点坐标为(-1,4),则下列说法正确的是 ( )
A. 二次函数图象的对称轴是直线x=1
B. 二次函数图象与x轴的另一个交点的横坐标是2
C. 当x<-1时,y随x的增大而减小
D. 二次函数图象与y轴的交点的纵坐标是3
图3-12-9
D
图3-12-10
B
二、填空题
6. (2024·滨州)将抛物线y=-x2先向右平移1个单位长度,再向上平移2个单位长度,则平移后抛物线的顶点坐标为 .
7. (2024·宁夏)若二次函数y=2x2-x+m的图象与x轴有交点,则m的取值范围是 .
(1,2)
8. (2024·辽宁)如图3-12-11,在平面直角坐标系中,抛物线y=ax2+bx+3与x轴相交于点A,B,点B的坐标为(3,0),若点C(2,3)在抛物线上,则AB的长为 .
图3-12-11
4
三、解答题
9. (2023·宿迁)某商场销售A,B两种商品,每件进价均为20元. 调查发现,如果售出A种20件,B种10件,销售总额为840元;如果售出A种10件,B种15件,销售总额为660元.
(1)求A,B两种商品的销售单价;
(2)经市场调研,A种商品按原售价销售,可售出40件,原售价每降价1元,销售量可增加10件;B种商品的售价不变,A种的商品售价不低于B种商品的售价. 设A种商品降价m元,如果A,B两种商品的销售量相同,那么当m取何值时,商场销售A,B两种商品可获得总利润最大?最大利润是多少?
(2)∵A种的商品售价不低于B种商品的售价,∴30-m≥24. 解得m≤6.
设总利润为w元.
由题意,得w=(30-m-20)(40+10m)+(24-20)(40+10m)
=-10(m-5)2+810.
∵-10<0,且m≤6,
∴当m=5时,w有最大值,最大值为810.
答:当m=5时,商场销售A,B两种商品可获得总利润最大,最大利润是810元.
图3-12-12
(2)点P是抛物线在第四象限图象上的任意一点,当△BCP的面积最大时,求BC边上的高PN的值.
图3-12-12
答图3-12-4
命题趋势
( 限时 5 分钟)
(综合运用)【问题背景】
如图3-12-13,抛物线y=-x2+bx+c交x轴于点A,交y轴于点B,已知经过点A,B的直线的表达式为y=x+3,点P(m,0)是线段AO上的一个动点,其中
-3
【构建联系】
(1)求抛物线的函数表达式;
(2)如图3-12-13①,作EF∥x轴,交直线AB于点F,四边形DEFG为矩形,当矩形DEFG的周长为9时,求m的值;
图3-12-13
(3)如图3-12-13②,作DE的中垂线MQ交AB于点M,交DE于点Q,在MQ延长线上取点N,使QN=4MQ,求点N到y轴的最远距离.
图3-12-13
图3-12-13
命题解读:根据最新课程标准和近三年中考命题动向,预测2025年中考命题方向可能注重考查二次函数的基本概念、图象与性质,如对称轴、顶点坐标、最值、图象的平移等;强调二次函数与其他数学知识的综合运用,可能与方程、不等式、其他函数、几何图形等综合考查;注重与实际问题的紧密结合,可能会出现经济、科技、生活等多个领域的实际情境.
同课章节目录
