中考数学复习知识梳理第三章函数第10课时一次函数课件(共54张PPT)
文档属性
| 名称 | 中考数学复习知识梳理第三章函数第10课时一次函数课件(共54张PPT) |  | |
| 格式 | ppt | ||
| 文件大小 | 8.0MB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 通用版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2025-05-31 09:51:06 | ||
图片预览








文档简介
(共54张PPT)
第三章 函 数
第9课时 平面直角坐标系与函数
课前循环练
(限时5分钟)
1. (广东真题)下列图形中,不是轴对称图形的是 ( )
A
2. (广东真题)下列等式正确的是 ( )
A. (-1)-3=1 B. (-4)0=1
C. (-2)2×(-2)3=-26 D. (-5)4÷(-5)2=-52
B
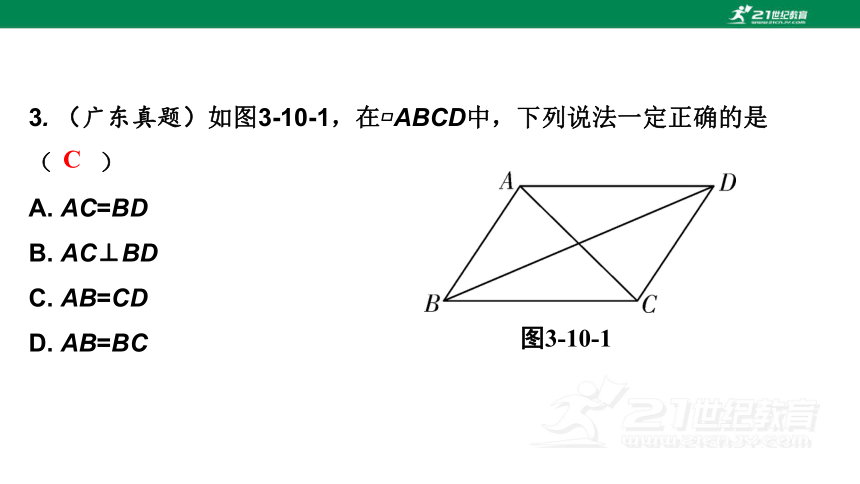
3. (广东真题)如图3-10-1,在 ABCD中,下列说法一定正确的是
( )
A. AC=BD
B. AC⊥BD
C. AB=CD
D. AB=BC
图3-10-1
C
4. (广东真题)在Rt△ABC中,∠ABC=90°,AB=3,BC=4,则sin A=
.
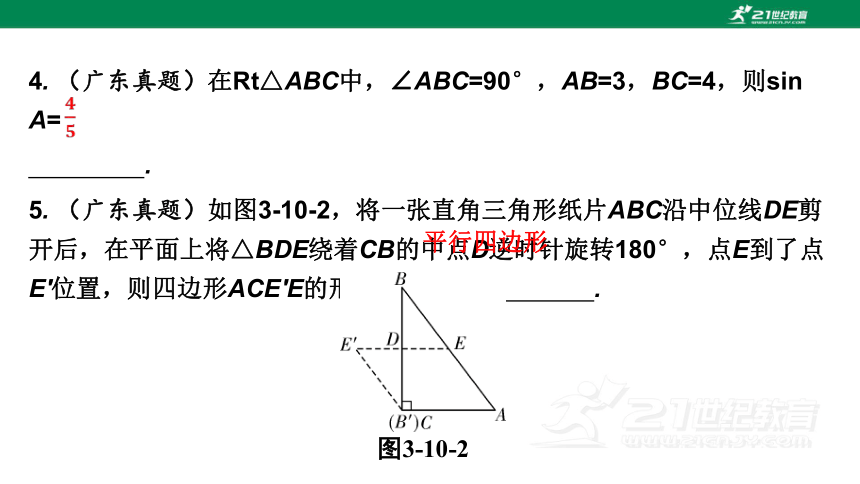
5. (广东真题)如图3-10-2,将一张直角三角形纸片ABC沿中位线DE剪开后,在平面上将△BDE绕着CB的中点D逆时针旋转180°,点E到了点E'位置,则四边形ACE'E的形状是 .
图3-10-2
平行四边形
①结合具体情境体会一次函数的意义,能根据已知条件确定一次函数的表达式;会运用待定系数法确定一次函数的表达式.
②能画一次函数的图象,根据图象和函数表达式y=kx+b(k≠0)探索并理解k>0和k<0时图象的变化情况;理解正比例函数.
③体会一次函数与二元一次方程的关系.
④能用一次函数解决简单实际问题.
课标要求
对接教材 人教:八下第十九章 一次函数
北师:八上第四章 一次函数
考点梳理
考点复习
1.一次函数与正比例函数
(1)一次函数:形如y=kx+b(k,b为常数,k≠0)的函数,叫做一次函数.
(2)正比例函数:在一次函数y=kx+b(k,b是常数,k≠0)中,当
时,它是一个正比例函数,即正比例函数是一种特殊的
b=0
一次函数
①②
②
2.一次函数的图象与性质
函数 系数取值 图象 经过的象限 函数的性质
y=kx
(k≠0) k>0
一、三 y随x的增大而增大
k<0
① y随x的增大而减小
二、四
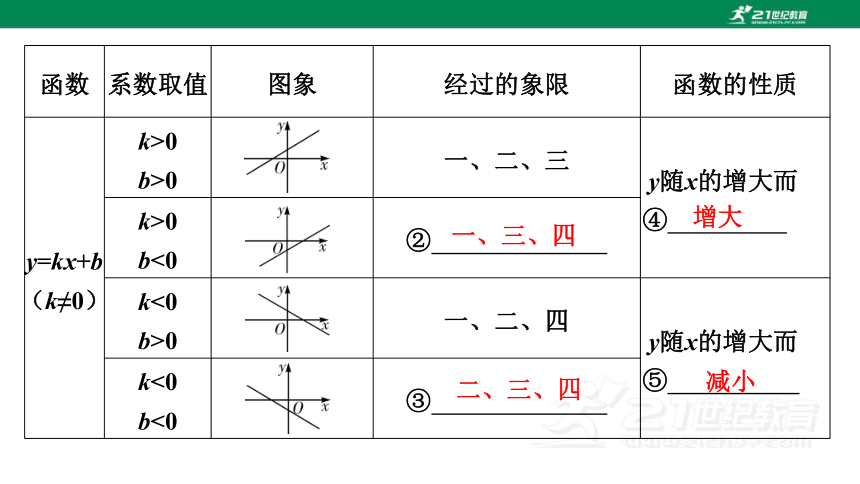
函数 系数取值 图象 经过的象限 函数的性质
y=kx+b
(k≠0) k>0
b>0 一、二、三 y随x的增大而
④
k>0
b<0 ②
k<0
b>0 一、二、四 y随x的增大而
⑤
k<0
b<0 ③
一、三、四
增大
二、三、四
减小
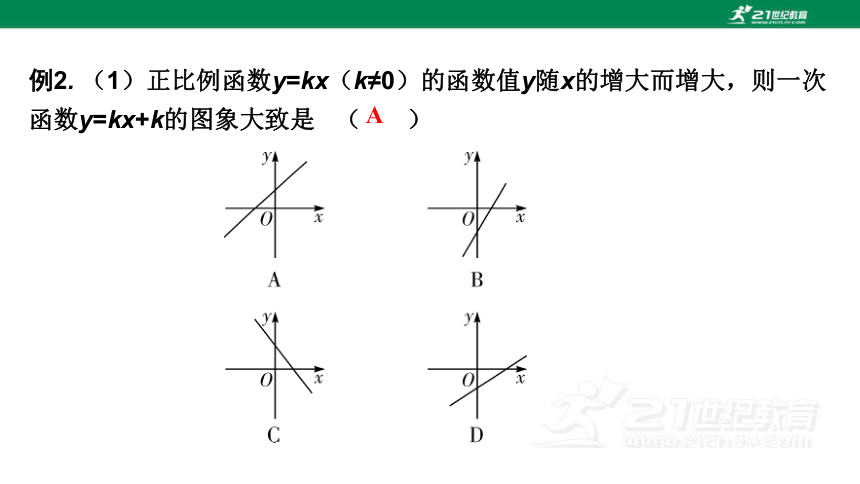
例2. (1)正比例函数y=kx(k≠0)的函数值y随x的增大而增大,则一次函数y=kx+k的图象大致是 ( )
A
(2)已知函数y=-2x+3.
①该函数图象经过第 象限,y随x的增大而 ;
②该函数图象与x轴的交点坐标为 ,与y轴的交点坐标为
;
③将该函数图象向左平移2个单位长度,可得直线 ;将该函数图象向下平移6个单位长度,可得直线 .
一、二、四
减小
(0,3)
y=-2x-1
y=-2x-3
3.用待定系数法确定一次函数的解析式
用待定系数法确定一次函数解析式的一般步骤:
(1)设:设出一次函数解析式的一般形式y=kx+b;
(2)列:将已知点的坐标代入函数解析式,得到方程(组);
(3)解:解方程(组),求出待定系数的值,写出一次函数的解析式
例3. 已知一次函数的图象经过A(-2,-3),B(1,3)两点,求这个一次函数的表达式.
(3)与一元一次不等式的关系:
①从“数”上看:不等式kx+b>0的解集 一次函数y=kx +b中,y>0时x的取值范围;不等式kx+b<0的解集 一次函数y=kx+b中,y<0时x的取值范围.
②从“形”上看:不等式kx+b>0的解集 一次函数y=kx+b的图象位于x轴上方部分对应的点的横坐标的取值范围;不等式kx+b<0的解集 一次函数y=kx +b的图象位于x轴下方部分对应的点的横坐标的取值范围
x=2
(3)如图3-10-3,一次函数y=kx+b的图象经过A,B两点,则不等式kx+b>0的解集是 .
图3-10-3
x<2
5.一次函数的应用
解一次函数应用题的一般步骤:
(1)找出问题中的变量和常量及它们之间的函数关系;
(2)列一次函数表达式表示它们之间的关系;
(3)应用一次函数的图象及性质解题;
(4)检验结果的合理性,检验是否符合实际意义
例5. (跨学科融合)一个弹簧不挂重物时长6 cm,挂上重物后,在弹性限度内弹簧伸长的长度与所挂重物的质量成正比.弹簧总长y(cm)关于所挂物体质量x(kg)的函数图象如图3-10-4所示,则图中a的值是( )
A. 3
B. 4
C. 5
D. 6
图3-10-4
A
广东中考
1. (2024·广东题10,3分,一次函数与一元一次不等式;一次函数的图象)已知不等式kx+b<0的解集是x<2,则一次函数y=kx+b的图象大致是
( )
B
2. (2023·广东题16〈2〉,5分,待定系数法求一次函数解析式)已知一次函数y=kx+b的图象经过点(0,1)与点(2,5),求该一次函数的表达式.
高分击破
【典型考点】待定系数法求一次函数的解析式 得分点分析
1. (教材改编)已知一次函数的图象经过点(4,-9)和点(6,3).
(1)求这个函数的解析式;
(2)求这个函数的图象与x轴的交点坐标.
温馨提示:此类考题常见于广东省中考数学试卷的第17题,分值一般为7分,答题时要注意书写格式,分步书写,慢做会求全对,评卷老师是分步给分的哦!
图3-10-5
(3)通过计算说明在此区间测速路段内,该辆汽车减速前是否超速. (此路段要求小型汽车行驶速度不得超过120 km/h)
图3-10-5
【典型错例】不会用绝对值表示距离和忽视分类讨论,导致漏解
3. 在平面直角坐标系xOy中,直线y=kx+b过点A(-6,0),且与y轴交于点B,直线与两坐标轴围成的△AOB的面积为12,求直线的表达式.
图3-10-6
(6,0)
(0,3)
图3-10-7
图3-10-7
生长变式:面积变式
(3)在(2)的条件下,若P是直线CD上的一个动点,当S△PBM=20时,求点P的坐标;
图3-10-7
种子成树:综合创新
(4)在(2)的条件下,F为直线AB上一动点,在平面直角坐标系内是否存在点N,使得以BF为一边,以B,D,F,N为顶点的四边形是菱形?若存在,求出点N的坐标;若不存在,请说明理由.
图3-10-7
图3-10-7
图3-10-7
中考演练
(限时15分钟)
一、选择题
1. (2024·兰州)一次函数y=2x-3的图象不经过 ( )
A. 第一象限 B. 第二象限 C. 第三象限 D. 第四象限
2. (2024·山西)已知点A(x1,y1),B(x2,y2)都在正比例函数y=3x的图象上,若x1A. y1>y2 B. y1B
B
A
4. (2024·山西,跨学科融合)生物学研究表明,某种蛇在一定生长阶段,其体长y(cm)是尾长x(cm)的一次函数,部分数据如下表所示,则y与x之间的关系式为 ( )
A. y=7.5x+0.5
B. y=7.5x-0.5
C. y=15x
D. y=15x+45.5
尾长x/cm 6 8 10
体长y/cm 45.5 60.5 75.5
A
图3-10-8
A
二、填空题
6. (2024·长春)已知直线y=kx+b(k,b是常数)经过点(1,1),且y随x的增大而减小,则b的值可以是 . (写出一个即可)
2(答案不唯一)
7. (2024·扬州)如图3-10-9,已知一次函数y=kx+b(k≠0)的图象分别与x,y轴交于A,B两点,若OA=2,OB=1,则关于x的方程kx+b=0的解为
.
图3-10-9
x=-2
8. (2024·凉山州)如图3-10-10,一次函数y=kx+b的图象经过A(3,6),B(0,3)两点,交x轴于点C,则△AOC的面积为 .
图3-10-10
9
三、解答题
9. (2024·北京)在平面直角坐标系xOy中,函数y=kx+b(k≠0)与y=-kx+3的图象交于点(2,1).
(1)求k,b的值;
(2)当x>2时,对于x的每一个值,函数y=mx(m≠0)的值既大于函数y=kx+b的值,也大于函数y=-kx+3的值,直接写出m的取值范围.
(2)m的取值范围是m≥1.
【提示】∵k=1,b=-1,
∴两函数的解析式分别为y=x-1,y=-x+3.
在同一平面直角坐标系中画出这两个函数的图象如答图3-10-1.
∵当x>2时,对于x的每一个值,函数y=mx的值大于函数y=x-1和y=-x+3的值,
∴当x>2时,函数y=mx的图象在函数y=x-1和y=-x+3图象的上方.
∴m的取值范围是m≥1.
答图3-10-1
10. (2024·广安)某小区物管中心计划采购A,B两种花卉用于美化环境. 已知购买2株A种花卉和3株B种花卉共需要21元;购买4株A种花卉和5株B种花卉共需要37元.
(1)求A,B两种花卉的单价;
(2)该物管中心计划采购A,B两种花卉共计10 000株,其中采购A种花卉的株数不超过B种花卉株数的4倍,当A,B两种花卉分别采购多少株时,总费用最少?并求出最少总费用.
(2)设采购A种花卉m株,则采购B种花卉(10 000-m)株.
由题意,得m≤4(10 000-m). 解得m≤8 000.
设总费用为w元.
则w=3m+5(10 000-m)=-2m+50 000. ∵-2<0,∴w随m的增大而减小.
∴当m=8 000时,w的值最小,w最小=-2×8 000+50 000=34 000.
此时10 000-m=2 000.
答:当采购A种花卉8 000株,B种花卉2 000株时,总费用最少,最少费用为34 000元.
命题趋势
( 限时 5 分钟)
(2024·吉林)综合与实践
某班同学分三个小组进行“板凳中的数学”的项目式学习研究. 第一小组负责调查板凳的历史及结构特点;第二小组负责研究板凳中蕴含的数学知识;第三小组负责汇报和交流. 下面是第三小组汇报的部分内容,请你阅读相关信息,并解答“建立模型”中的问题.
【背景调查】图3-10-11①中的板凳又叫“四脚八叉凳”,是中国传统家具,其榫卯结构体现了古人含蓄内敛的审美观. 榫眼的设计很有讲究,木工一般用铅笔画出凳面的对称轴,以对称轴为基准向两边各取相同的长度,确定榫眼的位置,如图3-10-11②所示. 板凳的结构设计体现了数学的对称美.
【收集数据】小组收集了一些板凳并进行了测量. 设以对称轴为基准向两边各取相同的长度为x(mm),凳面的宽度为y(mm),记录如下:
以对称轴为基准向两边各取相同的长度x/mm 16.5 19.8 23.1 26.4 29.7
凳面的宽度y/mm 115.5 132 148.5 165 181.5
【分析数据】如图3-10-11③,小组根据表中x,y的数值,在平面直角坐标系中描出了各点.
【建立模型】请你帮助小组解决下列问题:
图3-10-11
(1)观察上述各点的分布规律,它们是否在同一条直线上?如果在同一条直线上,求出这条直线所对应的函数解析式;如果不在同一条直线上,请说明理由;
图3-10-11
(2)当凳面宽度为213 mm时,以对称轴为基准向两边各取相同的长度是多少?
(2)把y=213代入y=5x+33,得5x+33=213. 解得x=36.
∴当凳面宽度为213 mm时,以对称轴为基准向两边各取相同的长度是36 mm.
图3-10-11
命题解读:根据最新课程标准和近三年中考命题动向,预测2025年中考命题方向可能注重考查一次函数的基本概念、图象与性质,如求函数的表达式、与坐标轴的交点等;强调与实际情境结合,可能出现购物、运输、交通等实际情境,还可能出现跨学科的情境;可能会与几何图形、方程、不等式等知识综合考查.
第三章 函 数
第9课时 平面直角坐标系与函数
课前循环练
(限时5分钟)
1. (广东真题)下列图形中,不是轴对称图形的是 ( )
A
2. (广东真题)下列等式正确的是 ( )
A. (-1)-3=1 B. (-4)0=1
C. (-2)2×(-2)3=-26 D. (-5)4÷(-5)2=-52
B
3. (广东真题)如图3-10-1,在 ABCD中,下列说法一定正确的是
( )
A. AC=BD
B. AC⊥BD
C. AB=CD
D. AB=BC
图3-10-1
C
4. (广东真题)在Rt△ABC中,∠ABC=90°,AB=3,BC=4,则sin A=
.
5. (广东真题)如图3-10-2,将一张直角三角形纸片ABC沿中位线DE剪开后,在平面上将△BDE绕着CB的中点D逆时针旋转180°,点E到了点E'位置,则四边形ACE'E的形状是 .
图3-10-2
平行四边形
①结合具体情境体会一次函数的意义,能根据已知条件确定一次函数的表达式;会运用待定系数法确定一次函数的表达式.
②能画一次函数的图象,根据图象和函数表达式y=kx+b(k≠0)探索并理解k>0和k<0时图象的变化情况;理解正比例函数.
③体会一次函数与二元一次方程的关系.
④能用一次函数解决简单实际问题.
课标要求
对接教材 人教:八下第十九章 一次函数
北师:八上第四章 一次函数
考点梳理
考点复习
1.一次函数与正比例函数
(1)一次函数:形如y=kx+b(k,b为常数,k≠0)的函数,叫做一次函数.
(2)正比例函数:在一次函数y=kx+b(k,b是常数,k≠0)中,当
时,它是一个正比例函数,即正比例函数是一种特殊的
b=0
一次函数
①②
②
2.一次函数的图象与性质
函数 系数取值 图象 经过的象限 函数的性质
y=kx
(k≠0) k>0
一、三 y随x的增大而增大
k<0
① y随x的增大而减小
二、四
函数 系数取值 图象 经过的象限 函数的性质
y=kx+b
(k≠0) k>0
b>0 一、二、三 y随x的增大而
④
k>0
b<0 ②
k<0
b>0 一、二、四 y随x的增大而
⑤
k<0
b<0 ③
一、三、四
增大
二、三、四
减小
例2. (1)正比例函数y=kx(k≠0)的函数值y随x的增大而增大,则一次函数y=kx+k的图象大致是 ( )
A
(2)已知函数y=-2x+3.
①该函数图象经过第 象限,y随x的增大而 ;
②该函数图象与x轴的交点坐标为 ,与y轴的交点坐标为
;
③将该函数图象向左平移2个单位长度,可得直线 ;将该函数图象向下平移6个单位长度,可得直线 .
一、二、四
减小
(0,3)
y=-2x-1
y=-2x-3
3.用待定系数法确定一次函数的解析式
用待定系数法确定一次函数解析式的一般步骤:
(1)设:设出一次函数解析式的一般形式y=kx+b;
(2)列:将已知点的坐标代入函数解析式,得到方程(组);
(3)解:解方程(组),求出待定系数的值,写出一次函数的解析式
例3. 已知一次函数的图象经过A(-2,-3),B(1,3)两点,求这个一次函数的表达式.
(3)与一元一次不等式的关系:
①从“数”上看:不等式kx+b>0的解集 一次函数y=kx +b中,y>0时x的取值范围;不等式kx+b<0的解集 一次函数y=kx+b中,y<0时x的取值范围.
②从“形”上看:不等式kx+b>0的解集 一次函数y=kx+b的图象位于x轴上方部分对应的点的横坐标的取值范围;不等式kx+b<0的解集 一次函数y=kx +b的图象位于x轴下方部分对应的点的横坐标的取值范围
x=2
(3)如图3-10-3,一次函数y=kx+b的图象经过A,B两点,则不等式kx+b>0的解集是 .
图3-10-3
x<2
5.一次函数的应用
解一次函数应用题的一般步骤:
(1)找出问题中的变量和常量及它们之间的函数关系;
(2)列一次函数表达式表示它们之间的关系;
(3)应用一次函数的图象及性质解题;
(4)检验结果的合理性,检验是否符合实际意义
例5. (跨学科融合)一个弹簧不挂重物时长6 cm,挂上重物后,在弹性限度内弹簧伸长的长度与所挂重物的质量成正比.弹簧总长y(cm)关于所挂物体质量x(kg)的函数图象如图3-10-4所示,则图中a的值是( )
A. 3
B. 4
C. 5
D. 6
图3-10-4
A
广东中考
1. (2024·广东题10,3分,一次函数与一元一次不等式;一次函数的图象)已知不等式kx+b<0的解集是x<2,则一次函数y=kx+b的图象大致是
( )
B
2. (2023·广东题16〈2〉,5分,待定系数法求一次函数解析式)已知一次函数y=kx+b的图象经过点(0,1)与点(2,5),求该一次函数的表达式.
高分击破
【典型考点】待定系数法求一次函数的解析式 得分点分析
1. (教材改编)已知一次函数的图象经过点(4,-9)和点(6,3).
(1)求这个函数的解析式;
(2)求这个函数的图象与x轴的交点坐标.
温馨提示:此类考题常见于广东省中考数学试卷的第17题,分值一般为7分,答题时要注意书写格式,分步书写,慢做会求全对,评卷老师是分步给分的哦!
图3-10-5
(3)通过计算说明在此区间测速路段内,该辆汽车减速前是否超速. (此路段要求小型汽车行驶速度不得超过120 km/h)
图3-10-5
【典型错例】不会用绝对值表示距离和忽视分类讨论,导致漏解
3. 在平面直角坐标系xOy中,直线y=kx+b过点A(-6,0),且与y轴交于点B,直线与两坐标轴围成的△AOB的面积为12,求直线的表达式.
图3-10-6
(6,0)
(0,3)
图3-10-7
图3-10-7
生长变式:面积变式
(3)在(2)的条件下,若P是直线CD上的一个动点,当S△PBM=20时,求点P的坐标;
图3-10-7
种子成树:综合创新
(4)在(2)的条件下,F为直线AB上一动点,在平面直角坐标系内是否存在点N,使得以BF为一边,以B,D,F,N为顶点的四边形是菱形?若存在,求出点N的坐标;若不存在,请说明理由.
图3-10-7
图3-10-7
图3-10-7
中考演练
(限时15分钟)
一、选择题
1. (2024·兰州)一次函数y=2x-3的图象不经过 ( )
A. 第一象限 B. 第二象限 C. 第三象限 D. 第四象限
2. (2024·山西)已知点A(x1,y1),B(x2,y2)都在正比例函数y=3x的图象上,若x1
B
A
4. (2024·山西,跨学科融合)生物学研究表明,某种蛇在一定生长阶段,其体长y(cm)是尾长x(cm)的一次函数,部分数据如下表所示,则y与x之间的关系式为 ( )
A. y=7.5x+0.5
B. y=7.5x-0.5
C. y=15x
D. y=15x+45.5
尾长x/cm 6 8 10
体长y/cm 45.5 60.5 75.5
A
图3-10-8
A
二、填空题
6. (2024·长春)已知直线y=kx+b(k,b是常数)经过点(1,1),且y随x的增大而减小,则b的值可以是 . (写出一个即可)
2(答案不唯一)
7. (2024·扬州)如图3-10-9,已知一次函数y=kx+b(k≠0)的图象分别与x,y轴交于A,B两点,若OA=2,OB=1,则关于x的方程kx+b=0的解为
.
图3-10-9
x=-2
8. (2024·凉山州)如图3-10-10,一次函数y=kx+b的图象经过A(3,6),B(0,3)两点,交x轴于点C,则△AOC的面积为 .
图3-10-10
9
三、解答题
9. (2024·北京)在平面直角坐标系xOy中,函数y=kx+b(k≠0)与y=-kx+3的图象交于点(2,1).
(1)求k,b的值;
(2)当x>2时,对于x的每一个值,函数y=mx(m≠0)的值既大于函数y=kx+b的值,也大于函数y=-kx+3的值,直接写出m的取值范围.
(2)m的取值范围是m≥1.
【提示】∵k=1,b=-1,
∴两函数的解析式分别为y=x-1,y=-x+3.
在同一平面直角坐标系中画出这两个函数的图象如答图3-10-1.
∵当x>2时,对于x的每一个值,函数y=mx的值大于函数y=x-1和y=-x+3的值,
∴当x>2时,函数y=mx的图象在函数y=x-1和y=-x+3图象的上方.
∴m的取值范围是m≥1.
答图3-10-1
10. (2024·广安)某小区物管中心计划采购A,B两种花卉用于美化环境. 已知购买2株A种花卉和3株B种花卉共需要21元;购买4株A种花卉和5株B种花卉共需要37元.
(1)求A,B两种花卉的单价;
(2)该物管中心计划采购A,B两种花卉共计10 000株,其中采购A种花卉的株数不超过B种花卉株数的4倍,当A,B两种花卉分别采购多少株时,总费用最少?并求出最少总费用.
(2)设采购A种花卉m株,则采购B种花卉(10 000-m)株.
由题意,得m≤4(10 000-m). 解得m≤8 000.
设总费用为w元.
则w=3m+5(10 000-m)=-2m+50 000. ∵-2<0,∴w随m的增大而减小.
∴当m=8 000时,w的值最小,w最小=-2×8 000+50 000=34 000.
此时10 000-m=2 000.
答:当采购A种花卉8 000株,B种花卉2 000株时,总费用最少,最少费用为34 000元.
命题趋势
( 限时 5 分钟)
(2024·吉林)综合与实践
某班同学分三个小组进行“板凳中的数学”的项目式学习研究. 第一小组负责调查板凳的历史及结构特点;第二小组负责研究板凳中蕴含的数学知识;第三小组负责汇报和交流. 下面是第三小组汇报的部分内容,请你阅读相关信息,并解答“建立模型”中的问题.
【背景调查】图3-10-11①中的板凳又叫“四脚八叉凳”,是中国传统家具,其榫卯结构体现了古人含蓄内敛的审美观. 榫眼的设计很有讲究,木工一般用铅笔画出凳面的对称轴,以对称轴为基准向两边各取相同的长度,确定榫眼的位置,如图3-10-11②所示. 板凳的结构设计体现了数学的对称美.
【收集数据】小组收集了一些板凳并进行了测量. 设以对称轴为基准向两边各取相同的长度为x(mm),凳面的宽度为y(mm),记录如下:
以对称轴为基准向两边各取相同的长度x/mm 16.5 19.8 23.1 26.4 29.7
凳面的宽度y/mm 115.5 132 148.5 165 181.5
【分析数据】如图3-10-11③,小组根据表中x,y的数值,在平面直角坐标系中描出了各点.
【建立模型】请你帮助小组解决下列问题:
图3-10-11
(1)观察上述各点的分布规律,它们是否在同一条直线上?如果在同一条直线上,求出这条直线所对应的函数解析式;如果不在同一条直线上,请说明理由;
图3-10-11
(2)当凳面宽度为213 mm时,以对称轴为基准向两边各取相同的长度是多少?
(2)把y=213代入y=5x+33,得5x+33=213. 解得x=36.
∴当凳面宽度为213 mm时,以对称轴为基准向两边各取相同的长度是36 mm.
图3-10-11
命题解读:根据最新课程标准和近三年中考命题动向,预测2025年中考命题方向可能注重考查一次函数的基本概念、图象与性质,如求函数的表达式、与坐标轴的交点等;强调与实际情境结合,可能出现购物、运输、交通等实际情境,还可能出现跨学科的情境;可能会与几何图形、方程、不等式等知识综合考查.
同课章节目录
