中考数学复习知识梳理第七章尺规作图及图形变换第26课时图形的对称、平移、旋转与折叠课件(共62张PPT)
文档属性
| 名称 | 中考数学复习知识梳理第七章尺规作图及图形变换第26课时图形的对称、平移、旋转与折叠课件(共62张PPT) |  | |
| 格式 | ppt | ||
| 文件大小 | 11.3MB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 通用版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2025-05-31 09:57:06 | ||
图片预览








文档简介
(共62张PPT)
第七章 尺规作图及图形变换
第26课时 图形的对称、平移、旋转与折叠
课前循环练
(限时5分钟)
D
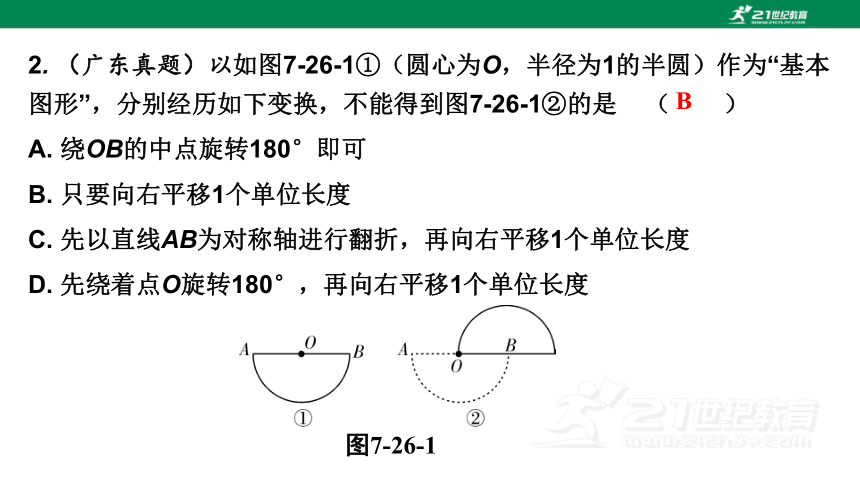
2. (广东真题)以如图7-26-1①(圆心为O,半径为1的半圆)作为“基本图形”,分别经历如下变换,不能得到图7-26-1②的是 ( )
A. 绕OB的中点旋转180°即可
B. 只要向右平移1个单位长度
C. 先以直线AB为对称轴进行翻折,再向右平移1个单位长度
D. 先绕着点O旋转180°,再向右平移1个单位长度
图7-26-1
B
图7-26-2
C
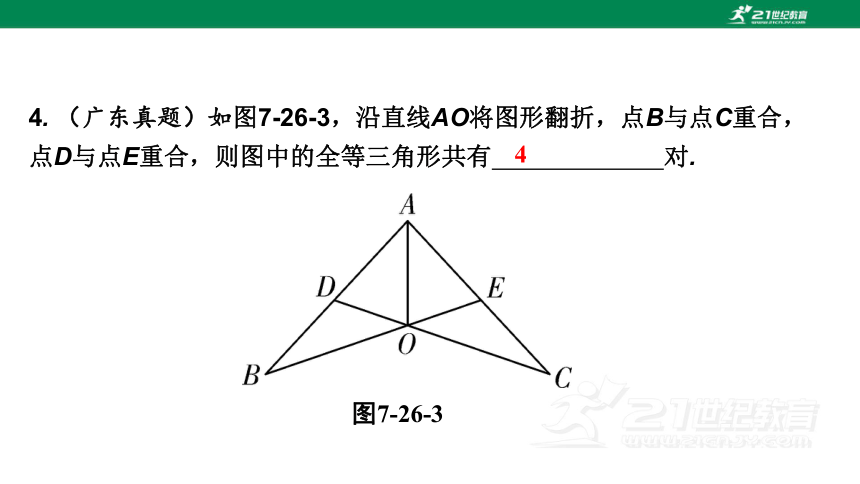
4. (广东真题)如图7-26-3,沿直线AO将图形翻折,点B与点C重合,点D与点E重合,则图中的全等三角形共有 对.
图7-26-3
4
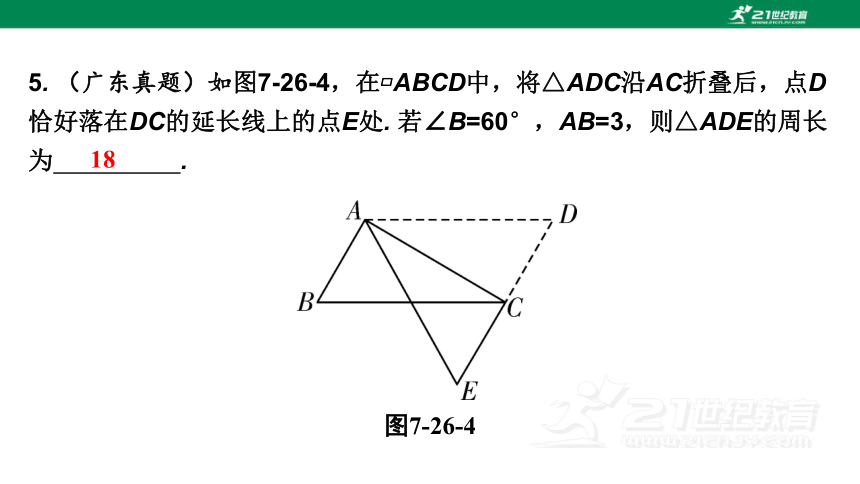
5. (广东真题)如图7-26-4,在 ABCD中,将△ADC沿AC折叠后,点D恰好落在DC的延长线上的点E处. 若∠B=60°,AB=3,则△ADE的周长为 .
图7-26-4
18
(1)图形的轴对称
①通过具体实例理解轴对称的概念,探索它的基本性质:成轴对称的两个图形中对应点的连线被对称轴垂直平分.
②能画出简单平面图形(点、线段、直线、三角形等)关于给定对称轴的对称图形.
③理解轴对称图形的概念;探索等腰三角形、矩形、菱形、正多边形、圆的轴对称性质.
④认识并欣赏自然界和现实生活中的轴对称图形.
课标要求
(2)图形的旋转
①通过具体实例认识平面图形关于旋转中心的旋转. 探索它的基本性质:一个图形和旋转得到的图形中,对应点到旋转中心距离相等,两组对应点分别与旋转中心连线所成的角相等.
②了解中心对称、中心对称图形的概念,探索它们的基本性质:成中心对称的两个图形中,对应点的连线经过对称中心,且被对称中心平分.
③探索线段、平行四边形、正多边形、圆的中心对称性质.
④认识并欣赏自然界和现实生活中的中心对称图形.
(3)图形的平移
①通过具体实例认识平移,探索它的基本性质:一个图形和它经过平移所得的图形中,两组对应点的连线平行(或在同一条直线上)且相等.
②认识并欣赏平移在自然界和现实生活中的应用.
③运用图形的轴对称、旋转、平移进行图案设计.
对接教材 人教:七下第五章 相交线与平行线(5.4平移);八上第十三章 轴对称;
九上第二十三章 旋转
北师:七下第五章 生活中的轴对称;八下第三章 图形的平移与旋转
考点梳理
考点复习
1.轴对称的性质
在轴对称图形或两个成轴对称的图形中,对应点所连的线段被对称轴
,对应线段 ,对应角
垂直平分
相等
相等
广东省对应考点例题
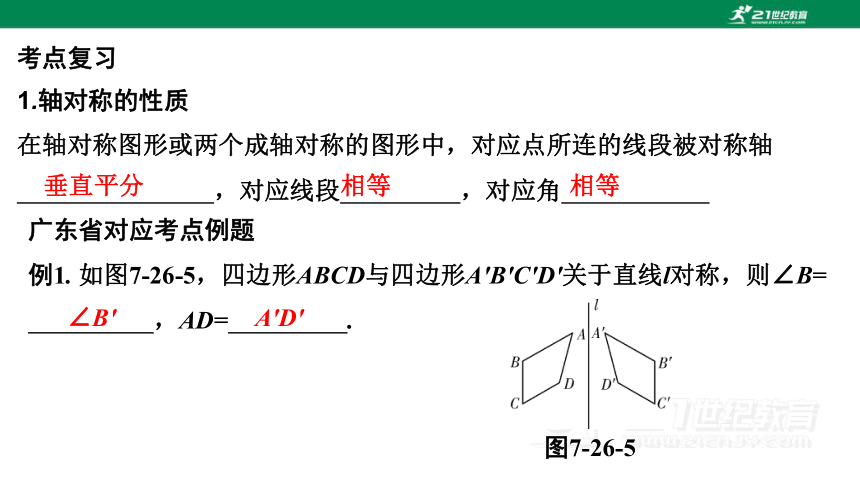
例1. 如图7-26-5,四边形ABCD与四边形A'B'C'D'关于直线l对称,则∠B=
,AD= .
图7-26-5
∠B'
A'D'
2.中心对称的性质
(1)成中心对称的两个图形中,对应点所连线段经过 且被对称中心 .
(2)中心对称的两个图形 .
(3)中心对称的两个图形,其对应线段互相 (或在同一直线上)且
对称中心
平分
全等
平行
相等
例2. 如图7-26-6,若四边形ABCD与四边形FGCE成中心对称,则它们的对称中心是 ,点A的对称点是 ,点E的对称点是 ,BD∥ 且BD= ,连接AF的线段经过 ,且被点C
,△ABD≌ .
图7-26-6
点C
点F
点D
GE
GE
点C
平分
△FGE
3.图形的平移
(1)平移:在平面内,将一个图形沿某个方向移动一定的距离,这样的图形运动称为平移.
(2)平移的性质
①平移只改变图形的位置,不改变图形的形状和大小;
②一个图形和它经过平移所得的图形中,对应点所连的线段平行(或在一条直线上)且 ;对应线段平行(或在一条直线上)且
,对应角 .
相等
相等
相等
x-a
y+b
y-b
例3. 如图7-26-7,在边长为1的小正方形网格中,△AOB的顶点均在格点上.
(1)点B关于y轴的对称点坐标为 ;
图7-26-7
(-2,2)
(2)将△AOB向左平移3个单位长度得到△A1O1B1,请画出△A1O1B1;
(3)在(2)的条件下,点A1的坐标为 .
答图7-26-1
图7-26-7
解:(2)如答图7-26-1,△A1O1B1即为所作.
(-2,3)
4.图形的旋转
(1)旋转:在平面内,将一个图形绕一个 按某个方向转动一个角度,这样的图形运动称为旋转.这个定点称为 ,转动的角称为 .
(2)旋转的性质
①旋转不改变图形的形状和大小;
②对应点到旋转中心的距离 ;
③任意一组对应点与 的连线所成的角都等于旋转角;
④对应线段 ,对应角
定点
旋转中心
旋转角
相等
旋转中心
相等
相等
例4. 如图7-26-8,已知△ABC三个顶点坐标分别是A(1,3),B(4,1),C(4,4).
(1)画出△ABC向左平移5个单位长度后得到的△A1B1C1;
(2)画出△ABC绕着原点O顺时针旋转90°后得到的△A2B2C2.
图7-26-8
答图7-26-2
解:(1)如答图7-26-2,△A1B1C1即为所作.
(2)如答图7-26-2,△A2B2C2即为所作.
5.图形翻折的性质
(1)翻折后得到的图形与原图形形状相同、大小不变,并且对应角、对应线段相等.
(2)折痕所在的直线即为翻折前后两个图形的 .
(3)翻折后,图形对应点所连的线段被对称轴垂直且平分
对称轴
例5. 如图7-26-9,把△ABC沿EF翻折.若∠A=60°,∠1=80°,则∠2的度数为 .
图7-26-9
40°
广东中考
1. (2024·广东题2,3分,中心对称图形;轴对称图形)下列几何图形中,既是中心对称图形也是轴对称图形的是 ( )
C
2. (2023·广东题2,3分,轴对称图形)下列出版社的商标图案中,是轴对称图形的为 ( )
A
图7-26-10
D
4. (2021·广东题23,8分,正方形的性质;翻折变换)如图7-26-11,边长为1的正方形ABCD中,E为AD的中点. 连接BE,将△ABE沿BE折叠得到△FBE,BF交AC于点G,求CG的长.
图7-26-11
答图7-26-3
答图7-26-3
高分击破
【典型考点】几何变换综合题 得分点分析
1. (2024·东营)在Rt△ABC中,∠ACB=90°,AC=1,BC=3.
(1)问题发现
如图7-26-12①,将△CAB绕点C按逆时针方向旋转90°得到△CDE,连接AD,BE,线段AD与BE的数量关系是 ,AD与BE的位置关系是 ;
图7-26-12
图7-26-12
(2)类比探究
将△CAB绕点C按逆时针方向旋转任意角度得到△CDE,连接AD,BE,线段AD与BE的数量关系、位置关系与(1)中结论是否一致?若AD交CE于点N,请结合图7-26-12②说明理由;
图7-26-12
图7-26-14
(3)迁移应用
如图7-26-12③,将△CAB绕点C旋转一定角度得到△CDE,当点D落到AB边上时,连接BE,求线段BE的长.
图7-26-12
图7-26-15
温馨提示:此类考题常见于广东省中考数学试卷的第22题,分值一般为13分,答题时要注意书写格式,分步书写,慢做会求全对,评卷老师是分步给分的哦!
【典型错例】逻辑不严谨,忽略“三点共线”的证明
2. 如图7-26-16,矩形ABCD的边长AB=4,AD=2,将矩形纸片沿EF折叠,使点A与点C重合.若点P为EF的中点,求CP的长.
图7-26-16
解:如答图7-26-4,连接AC,AE.
∵四边形ABCD为矩形,
∴AB∥CD,BC=AD=2,∠B=90°.
∴∠PEC=∠PFA.
答图7-26-4
答图7-26-4
错解分析
错解:如图7-26-17,连接AP.
∵四边形ABCD为矩形,
∴AB∥CD,BC=AD=2,∠B=90°.
∴∠PEC=∠PFA.
∵P为EF的中点,∴PE=PF.
又∵∠CPE=∠APF,
∴△CPE≌△APF(ASA).∴CP=AP.
图7-26-17
【生长式训练】知识生长→变式创新
3. (中考创新,原创题)在△ABC中,AB=6,AC=5,D,E分别AB,AC上的一点,连接DE.
知识种子:基本概念
(1)如图7-26-18,将△ADE沿直线DE折叠,使点A落在BC边上的点F处.若AD=BD,∠B=50°,则∠BDF的度数为 ;
图7-26-18
80°
种子生长:折叠问题
(2)如图7-26-19,将△ADE沿直线DE折叠,使得点A与点C重合.若BC=5,求AD的长;
图7-26-19
答图7-26-5
图7-26-20
图7-26-20
种子成树:综合创新
(4)在图7-26-20②中,延长BD,分别交AC,CE于点F,P,连接AP,得到图7-26-21.探究∠APE与∠ABC之间的数量关系,并说明理由.
图7-26-21
解:∠APE=∠ABC.
理由:由(3)知△BAD∽△CAE,
∴∠ABD=∠ACE,即∠ABP=∠ACP.
∴A,B,C,P四点共圆,如答图7-26-6所示.
∴四边形ABCP为圆的内接四边形.
∴∠ABC+∠APC=180°.
又∵∠APC+∠APE=180°,
∴∠APE=∠ABC.
答图7-26-6
中考演练
(限时15分钟)
一、选择题
1. (2024·赤峰)在以下绿色食品、回收、节能、节水四个标志中,是轴对称图形的是 ( )
A
2. (2024·内江)2024年6月5日,是二十四节气的芒种,二十四节气是中国劳动人民独创的文化遗产,能反映季节的变化,指导农事活动. 下面四幅图片分别代表“芒种”“白露”“立夏”“大雪”,其中是中心对称图形的是 ( )
D
3. (2024·盐城)下列四幅图片中的主体事物,在现实运动中属于翻折的是 ( )
C
4. (2024·无锡)如图7-26-22,在△ABC中,∠B=80°,∠C=65°,将△ABC绕点A逆时针旋转得到△AB'C'. 当AB'落在AC上时,∠BAC'的度数为 ( )
A. 65°
B. 70°
C. 80°
D. 85°
图7-26-22
B
图7-26-23
A
二、填空题
6. (2023·张家界)如图7-26-24,AO为∠BAC的平分线,且∠BAC=50°,将四边形ABOC绕点A逆时针方向旋转后,得到四边形AB'O'C',且∠OAC'=100°,则四边形ABOC旋转的角度是 .
图7-26-24
75°
7. (2024·河南)如图7-26-25,在平面直角坐标系中,正方形ABCD的边AB在x轴上,点A的坐标为(-2,0),点E在边CD上. 将△BCE沿BE折叠,点C落在点F处. 若点F的坐标为(0,6),则点E的坐标为 .
图7-26-25
(3,10)
图7-26-26
5
三、解答题
9. (2024·齐齐哈尔节选,数学文化)综合与实践
如图7-26-27①,这个图案是3世纪我国汉代的赵爽在注解《周髀算经》时给出的,人们称它为“赵爽弦图”,受这幅图的启发,数学兴趣小组建立了“一线三直角模型”. 如图7-26-27②,在△ABC中,∠A=90°,将线段BC绕点B顺时针旋转90°得到线段BD,作DE⊥AB交AB的延长线于点E.
图7-26-27
(1)【观察感知】如图7-26-27②,通过观察,线段AB与DE的数量关系是 ;
图7-26-27
AB=DE
(2)【问题解决】如图7-26-27③,连接CD并延长交AB的延长线于点F.若AB=2,AC=6,求△BDF的面积.
图7-26-27
图7-26-27
10. (2024·湖北节选)在矩形ABCD中,点E,F分别在边AD,BC上,将矩形ABCD沿EF折叠,使点A的对应点P落在边CD上,点B的对应点为点G,PG交BC于点H.
(1)如图7-26-28①,求证:△DEP∽△CPH;
(1)证明:∵四边形ABCD是矩形,
∴∠A=∠D=∠C=90°.∴∠DEP+∠DPE=90°.
由折叠的性质,得∠EPH=∠A=90°.
∴∠CPH+∠DPE=90°.
∴∠DEP=∠CPH.∴△DEP∽△CPH.
图7-26-28
(2)如图7-26-28②,当P为CD的中点,AB=2,AD=3时,求GH的长.
图7-26-28
命题趋势
( 限时 5 分钟)
(创新题)如图7-26-29①,△ABC和△ADE都是等腰直角三角形,∠BAC=∠DAE=90°,当点B在线段AD上,点C在线段AE上时,我们很容易得到BD=CE,不需证明.
图7-26-29
(1)如图7-26-29②,将△ADE绕点A逆时针旋转α(0<α<90°),连接BD,CE,此时BD=CE是否仍然成立?请说明理由;
解:(1)仍然成立.
理由:∵△ABC和△ADE都是等腰直角三角形,
∴AB=AC,AD=AE.
∵将△ADE绕点A逆时针旋转α,
∴∠BAD=∠CAE=α.
∴△ABD≌△ACE(SAS).∴BD=CE.
图7-26-29
图7-26-29
(3)在(2)的条件下,若P为DE中点,连接BP,当△ADE绕点A逆时针旋转时,直接写出BP的最大值.
答图7-26-7
命题解读:根据最新课程标准和近三年中考命题动向,预测2025年中考命题方向可能注重对图形变换基本概念和性质的考查,如判断轴对称图形、中心对称图形等,可能结合数学文化或科技领域背景考查;强调与三角形、四边形等几何图形的综合运用,可能涉及三角形的相似、勾股定理、方程等知识;还可能会考查综合探究类题型,通过平移、旋转、折叠变换图形或构造特殊图形综合考查.
第七章 尺规作图及图形变换
第26课时 图形的对称、平移、旋转与折叠
课前循环练
(限时5分钟)
D
2. (广东真题)以如图7-26-1①(圆心为O,半径为1的半圆)作为“基本图形”,分别经历如下变换,不能得到图7-26-1②的是 ( )
A. 绕OB的中点旋转180°即可
B. 只要向右平移1个单位长度
C. 先以直线AB为对称轴进行翻折,再向右平移1个单位长度
D. 先绕着点O旋转180°,再向右平移1个单位长度
图7-26-1
B
图7-26-2
C
4. (广东真题)如图7-26-3,沿直线AO将图形翻折,点B与点C重合,点D与点E重合,则图中的全等三角形共有 对.
图7-26-3
4
5. (广东真题)如图7-26-4,在 ABCD中,将△ADC沿AC折叠后,点D恰好落在DC的延长线上的点E处. 若∠B=60°,AB=3,则△ADE的周长为 .
图7-26-4
18
(1)图形的轴对称
①通过具体实例理解轴对称的概念,探索它的基本性质:成轴对称的两个图形中对应点的连线被对称轴垂直平分.
②能画出简单平面图形(点、线段、直线、三角形等)关于给定对称轴的对称图形.
③理解轴对称图形的概念;探索等腰三角形、矩形、菱形、正多边形、圆的轴对称性质.
④认识并欣赏自然界和现实生活中的轴对称图形.
课标要求
(2)图形的旋转
①通过具体实例认识平面图形关于旋转中心的旋转. 探索它的基本性质:一个图形和旋转得到的图形中,对应点到旋转中心距离相等,两组对应点分别与旋转中心连线所成的角相等.
②了解中心对称、中心对称图形的概念,探索它们的基本性质:成中心对称的两个图形中,对应点的连线经过对称中心,且被对称中心平分.
③探索线段、平行四边形、正多边形、圆的中心对称性质.
④认识并欣赏自然界和现实生活中的中心对称图形.
(3)图形的平移
①通过具体实例认识平移,探索它的基本性质:一个图形和它经过平移所得的图形中,两组对应点的连线平行(或在同一条直线上)且相等.
②认识并欣赏平移在自然界和现实生活中的应用.
③运用图形的轴对称、旋转、平移进行图案设计.
对接教材 人教:七下第五章 相交线与平行线(5.4平移);八上第十三章 轴对称;
九上第二十三章 旋转
北师:七下第五章 生活中的轴对称;八下第三章 图形的平移与旋转
考点梳理
考点复习
1.轴对称的性质
在轴对称图形或两个成轴对称的图形中,对应点所连的线段被对称轴
,对应线段 ,对应角
垂直平分
相等
相等
广东省对应考点例题
例1. 如图7-26-5,四边形ABCD与四边形A'B'C'D'关于直线l对称,则∠B=
,AD= .
图7-26-5
∠B'
A'D'
2.中心对称的性质
(1)成中心对称的两个图形中,对应点所连线段经过 且被对称中心 .
(2)中心对称的两个图形 .
(3)中心对称的两个图形,其对应线段互相 (或在同一直线上)且
对称中心
平分
全等
平行
相等
例2. 如图7-26-6,若四边形ABCD与四边形FGCE成中心对称,则它们的对称中心是 ,点A的对称点是 ,点E的对称点是 ,BD∥ 且BD= ,连接AF的线段经过 ,且被点C
,△ABD≌ .
图7-26-6
点C
点F
点D
GE
GE
点C
平分
△FGE
3.图形的平移
(1)平移:在平面内,将一个图形沿某个方向移动一定的距离,这样的图形运动称为平移.
(2)平移的性质
①平移只改变图形的位置,不改变图形的形状和大小;
②一个图形和它经过平移所得的图形中,对应点所连的线段平行(或在一条直线上)且 ;对应线段平行(或在一条直线上)且
,对应角 .
相等
相等
相等
x-a
y+b
y-b
例3. 如图7-26-7,在边长为1的小正方形网格中,△AOB的顶点均在格点上.
(1)点B关于y轴的对称点坐标为 ;
图7-26-7
(-2,2)
(2)将△AOB向左平移3个单位长度得到△A1O1B1,请画出△A1O1B1;
(3)在(2)的条件下,点A1的坐标为 .
答图7-26-1
图7-26-7
解:(2)如答图7-26-1,△A1O1B1即为所作.
(-2,3)
4.图形的旋转
(1)旋转:在平面内,将一个图形绕一个 按某个方向转动一个角度,这样的图形运动称为旋转.这个定点称为 ,转动的角称为 .
(2)旋转的性质
①旋转不改变图形的形状和大小;
②对应点到旋转中心的距离 ;
③任意一组对应点与 的连线所成的角都等于旋转角;
④对应线段 ,对应角
定点
旋转中心
旋转角
相等
旋转中心
相等
相等
例4. 如图7-26-8,已知△ABC三个顶点坐标分别是A(1,3),B(4,1),C(4,4).
(1)画出△ABC向左平移5个单位长度后得到的△A1B1C1;
(2)画出△ABC绕着原点O顺时针旋转90°后得到的△A2B2C2.
图7-26-8
答图7-26-2
解:(1)如答图7-26-2,△A1B1C1即为所作.
(2)如答图7-26-2,△A2B2C2即为所作.
5.图形翻折的性质
(1)翻折后得到的图形与原图形形状相同、大小不变,并且对应角、对应线段相等.
(2)折痕所在的直线即为翻折前后两个图形的 .
(3)翻折后,图形对应点所连的线段被对称轴垂直且平分
对称轴
例5. 如图7-26-9,把△ABC沿EF翻折.若∠A=60°,∠1=80°,则∠2的度数为 .
图7-26-9
40°
广东中考
1. (2024·广东题2,3分,中心对称图形;轴对称图形)下列几何图形中,既是中心对称图形也是轴对称图形的是 ( )
C
2. (2023·广东题2,3分,轴对称图形)下列出版社的商标图案中,是轴对称图形的为 ( )
A
图7-26-10
D
4. (2021·广东题23,8分,正方形的性质;翻折变换)如图7-26-11,边长为1的正方形ABCD中,E为AD的中点. 连接BE,将△ABE沿BE折叠得到△FBE,BF交AC于点G,求CG的长.
图7-26-11
答图7-26-3
答图7-26-3
高分击破
【典型考点】几何变换综合题 得分点分析
1. (2024·东营)在Rt△ABC中,∠ACB=90°,AC=1,BC=3.
(1)问题发现
如图7-26-12①,将△CAB绕点C按逆时针方向旋转90°得到△CDE,连接AD,BE,线段AD与BE的数量关系是 ,AD与BE的位置关系是 ;
图7-26-12
图7-26-12
(2)类比探究
将△CAB绕点C按逆时针方向旋转任意角度得到△CDE,连接AD,BE,线段AD与BE的数量关系、位置关系与(1)中结论是否一致?若AD交CE于点N,请结合图7-26-12②说明理由;
图7-26-12
图7-26-14
(3)迁移应用
如图7-26-12③,将△CAB绕点C旋转一定角度得到△CDE,当点D落到AB边上时,连接BE,求线段BE的长.
图7-26-12
图7-26-15
温馨提示:此类考题常见于广东省中考数学试卷的第22题,分值一般为13分,答题时要注意书写格式,分步书写,慢做会求全对,评卷老师是分步给分的哦!
【典型错例】逻辑不严谨,忽略“三点共线”的证明
2. 如图7-26-16,矩形ABCD的边长AB=4,AD=2,将矩形纸片沿EF折叠,使点A与点C重合.若点P为EF的中点,求CP的长.
图7-26-16
解:如答图7-26-4,连接AC,AE.
∵四边形ABCD为矩形,
∴AB∥CD,BC=AD=2,∠B=90°.
∴∠PEC=∠PFA.
答图7-26-4
答图7-26-4
错解分析
错解:如图7-26-17,连接AP.
∵四边形ABCD为矩形,
∴AB∥CD,BC=AD=2,∠B=90°.
∴∠PEC=∠PFA.
∵P为EF的中点,∴PE=PF.
又∵∠CPE=∠APF,
∴△CPE≌△APF(ASA).∴CP=AP.
图7-26-17
【生长式训练】知识生长→变式创新
3. (中考创新,原创题)在△ABC中,AB=6,AC=5,D,E分别AB,AC上的一点,连接DE.
知识种子:基本概念
(1)如图7-26-18,将△ADE沿直线DE折叠,使点A落在BC边上的点F处.若AD=BD,∠B=50°,则∠BDF的度数为 ;
图7-26-18
80°
种子生长:折叠问题
(2)如图7-26-19,将△ADE沿直线DE折叠,使得点A与点C重合.若BC=5,求AD的长;
图7-26-19
答图7-26-5
图7-26-20
图7-26-20
种子成树:综合创新
(4)在图7-26-20②中,延长BD,分别交AC,CE于点F,P,连接AP,得到图7-26-21.探究∠APE与∠ABC之间的数量关系,并说明理由.
图7-26-21
解:∠APE=∠ABC.
理由:由(3)知△BAD∽△CAE,
∴∠ABD=∠ACE,即∠ABP=∠ACP.
∴A,B,C,P四点共圆,如答图7-26-6所示.
∴四边形ABCP为圆的内接四边形.
∴∠ABC+∠APC=180°.
又∵∠APC+∠APE=180°,
∴∠APE=∠ABC.
答图7-26-6
中考演练
(限时15分钟)
一、选择题
1. (2024·赤峰)在以下绿色食品、回收、节能、节水四个标志中,是轴对称图形的是 ( )
A
2. (2024·内江)2024年6月5日,是二十四节气的芒种,二十四节气是中国劳动人民独创的文化遗产,能反映季节的变化,指导农事活动. 下面四幅图片分别代表“芒种”“白露”“立夏”“大雪”,其中是中心对称图形的是 ( )
D
3. (2024·盐城)下列四幅图片中的主体事物,在现实运动中属于翻折的是 ( )
C
4. (2024·无锡)如图7-26-22,在△ABC中,∠B=80°,∠C=65°,将△ABC绕点A逆时针旋转得到△AB'C'. 当AB'落在AC上时,∠BAC'的度数为 ( )
A. 65°
B. 70°
C. 80°
D. 85°
图7-26-22
B
图7-26-23
A
二、填空题
6. (2023·张家界)如图7-26-24,AO为∠BAC的平分线,且∠BAC=50°,将四边形ABOC绕点A逆时针方向旋转后,得到四边形AB'O'C',且∠OAC'=100°,则四边形ABOC旋转的角度是 .
图7-26-24
75°
7. (2024·河南)如图7-26-25,在平面直角坐标系中,正方形ABCD的边AB在x轴上,点A的坐标为(-2,0),点E在边CD上. 将△BCE沿BE折叠,点C落在点F处. 若点F的坐标为(0,6),则点E的坐标为 .
图7-26-25
(3,10)
图7-26-26
5
三、解答题
9. (2024·齐齐哈尔节选,数学文化)综合与实践
如图7-26-27①,这个图案是3世纪我国汉代的赵爽在注解《周髀算经》时给出的,人们称它为“赵爽弦图”,受这幅图的启发,数学兴趣小组建立了“一线三直角模型”. 如图7-26-27②,在△ABC中,∠A=90°,将线段BC绕点B顺时针旋转90°得到线段BD,作DE⊥AB交AB的延长线于点E.
图7-26-27
(1)【观察感知】如图7-26-27②,通过观察,线段AB与DE的数量关系是 ;
图7-26-27
AB=DE
(2)【问题解决】如图7-26-27③,连接CD并延长交AB的延长线于点F.若AB=2,AC=6,求△BDF的面积.
图7-26-27
图7-26-27
10. (2024·湖北节选)在矩形ABCD中,点E,F分别在边AD,BC上,将矩形ABCD沿EF折叠,使点A的对应点P落在边CD上,点B的对应点为点G,PG交BC于点H.
(1)如图7-26-28①,求证:△DEP∽△CPH;
(1)证明:∵四边形ABCD是矩形,
∴∠A=∠D=∠C=90°.∴∠DEP+∠DPE=90°.
由折叠的性质,得∠EPH=∠A=90°.
∴∠CPH+∠DPE=90°.
∴∠DEP=∠CPH.∴△DEP∽△CPH.
图7-26-28
(2)如图7-26-28②,当P为CD的中点,AB=2,AD=3时,求GH的长.
图7-26-28
命题趋势
( 限时 5 分钟)
(创新题)如图7-26-29①,△ABC和△ADE都是等腰直角三角形,∠BAC=∠DAE=90°,当点B在线段AD上,点C在线段AE上时,我们很容易得到BD=CE,不需证明.
图7-26-29
(1)如图7-26-29②,将△ADE绕点A逆时针旋转α(0<α<90°),连接BD,CE,此时BD=CE是否仍然成立?请说明理由;
解:(1)仍然成立.
理由:∵△ABC和△ADE都是等腰直角三角形,
∴AB=AC,AD=AE.
∵将△ADE绕点A逆时针旋转α,
∴∠BAD=∠CAE=α.
∴△ABD≌△ACE(SAS).∴BD=CE.
图7-26-29
图7-26-29
(3)在(2)的条件下,若P为DE中点,连接BP,当△ADE绕点A逆时针旋转时,直接写出BP的最大值.
答图7-26-7
命题解读:根据最新课程标准和近三年中考命题动向,预测2025年中考命题方向可能注重对图形变换基本概念和性质的考查,如判断轴对称图形、中心对称图形等,可能结合数学文化或科技领域背景考查;强调与三角形、四边形等几何图形的综合运用,可能涉及三角形的相似、勾股定理、方程等知识;还可能会考查综合探究类题型,通过平移、旋转、折叠变换图形或构造特殊图形综合考查.
同课章节目录
