中考数学复习知识梳理第七章尺规作图及图形变换第25课时投影与视图课件(共44张PPT)
文档属性
| 名称 | 中考数学复习知识梳理第七章尺规作图及图形变换第25课时投影与视图课件(共44张PPT) |  | |
| 格式 | ppt | ||
| 文件大小 | 7.2MB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 通用版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2025-05-31 09:43:37 | ||
图片预览








文档简介
(共44张PPT)
第七章 尺规作图及图形变换
第25课时 投影与视图
课前循环练
(限时5分钟)
1. (广东真题)以下问题不适合全面调查的是 ( )
A. 调查某班学生每周课前预习的时间
B. 调查某中学在职教师的身体健康状况
C. 调查全国中小学生课外阅读情况
D. 调查某校篮球队员的身高
C
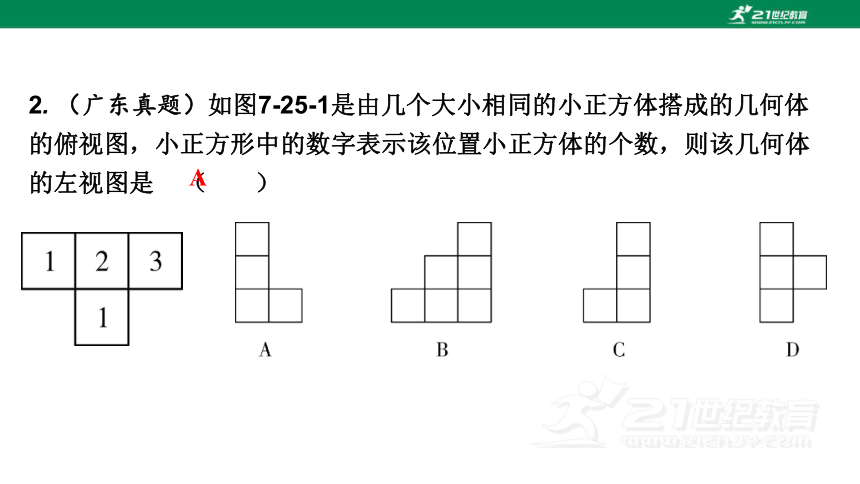
2. (广东真题)如图7-25-1是由几个大小相同的小正方体搭成的几何体的俯视图,小正方形中的数字表示该位置小正方体的个数,则该几何体的左视图是 ( )
A
3. (广东真题)将抛物线y=x2-4x-4向左平移3个单位长度,再向上平移5个单位长度,得到抛物线的函数表达式为 ( )
A. y=(x+1)2-13 B. y=(x-5)2-3
C. y=(x-5)2-13 D. y=(x+1)2-3
D
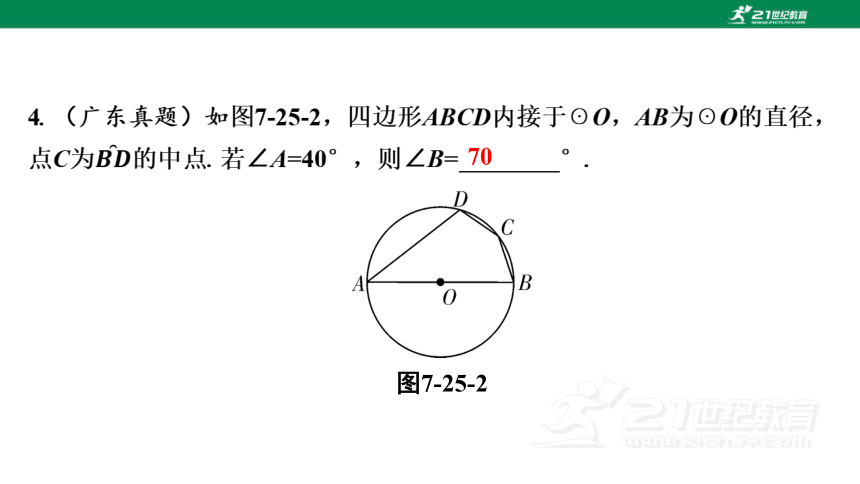
图7-25-2
70
5. (广东真题)某商店经销一种品牌的洗衣机,其中某一型号的洗衣机每台进价为a元,商店将进价提高20%后作为零售价进行销售,一段时间后,商店又以九折优惠价促销,这时该型号洗衣机的零售价为 元.
1.08a
①通过丰富的实例,了解中心投影和平行投影的概念.
②会画直棱柱、圆柱、圆锥、球的主视图、左视图、俯视图,能判断简单物体的视图,并会根据视图描述简单的几何体.
③了解直棱柱、圆锥的侧面展开图,能根据展开图想象和制作模型.
④通过实例,了解上述视图与展开图在现实生活中的应用.
课标要求
对接教材 人教:九下第二十九章 投影与视图
北师:七上第一章 丰富的图形世界;九上第五章 投影与视图
考点梳理
考点复习
1.投影
(1)中心投影:从 发出的光线所形成的投影称为中心投影.
(2)平行投影:由 光线所形成的投影称为平行投影.
(3)正投影:平行光线与投影面 时,这种投影称为正投影
一个点
平行
垂直
广东省对应考点例题
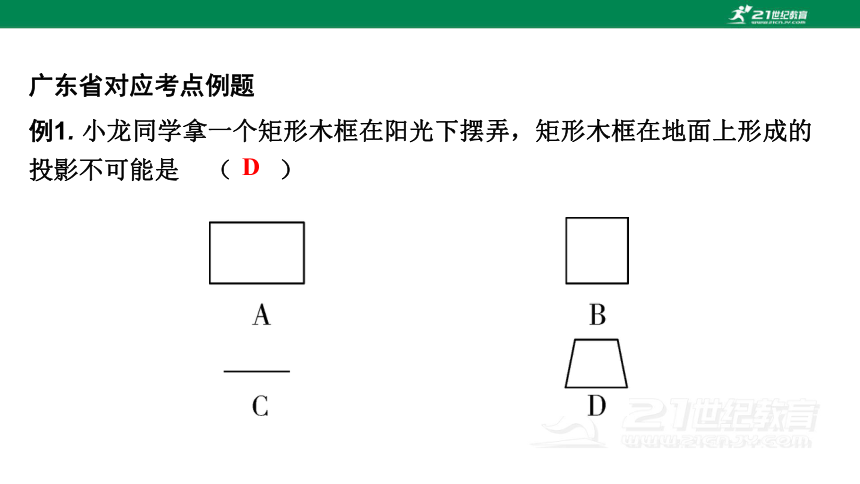
例1. 小龙同学拿一个矩形木框在阳光下摆弄,矩形木框在地面上形成的投影不可能是 ( )
D
2.三视图
视图:用 的方法绘制的物体在投影面上的图形,称为物体的视图.
(1)主视图:从 得到的视图叫做主视图;
(2)左视图:从 得到的视图叫做左视图;
(3)俯视图:从 得到的视图叫做俯视图
正投影
正面
左面
上面
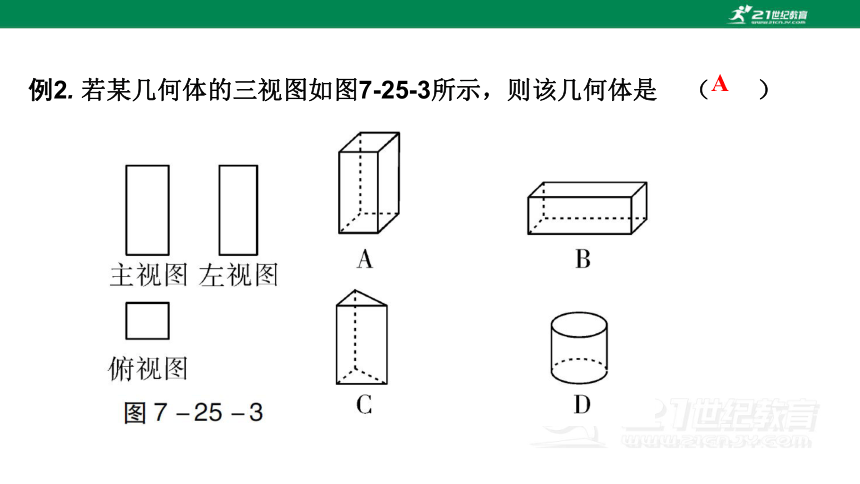
例2. 若某几何体的三视图如图7-25-3所示,则该几何体是 ( )
A
3.三视图的画法
(1)画三视图要注意三个方面:主视图与俯视图 ;主视图与左视图 ;左视图与俯视图 .简记为“主俯长对正,主左高平齐,左俯宽相等”.
(2)注意实线与虚线的区别:能看到的线用实线,看不到的线用虚线
长度相等
高度相等
宽度相等
例3. 6个完全相同的正方体组成如图7-25-4所示的几何体,画出该几何体的主视图和左视图(画在所给的方格中).
图7-25-4
解:如答图7-25-1.
答图7-25-1
4.几何体的展开与折叠
(1)常见几何体的展开图
长方体 圆柱 圆锥 正三棱柱
(2)正方体的展开图
①“一四一”型
②“二三一”型
③“三三”型 ④“二二二”型
例4. (1)下列展开图中,是正方体展开图的是 ( )
(2)下列图形中,为圆柱的侧面展开图的是 ( )
C
D
(3)如图7-25-5是一个直三棱柱,试画出它的侧面展开图,并求侧面展开图的面积.
图7-25-5
解:(3)直三棱柱的侧面展开图如答图7-25-2.
S侧面=(1.5+2+2.5)×3=18.
答图7-25-2
广东中考
1. (2019·广东题3,3分,简单组合体的三视图)如图7-25-6,由4个相同正方体组合而成的几何体,它的左视图是 ( )
A
如图7-25-6
2. (2021·广东题6,3分,几何体的展开图)如图7-25-7所示的图形是正方体展开图的有 ( )
A. 1个 B. 2个 C. 3个 D. 4个
图7-25-7
C
高分击破
【典型考点】三视图;几何体的展开图
1. (2024·宁夏)用5个大小相同的小正方体搭一个几何体,其主视图、左视图如图7-25-8②,现将其中4个小正方体按图7-25-8①方式摆放,则最后一个小正方体应放在 ( )
A. ①号位置 B. ②号位置
C. ③号位置 D. ④号位置
B
图7-25-8
2. (2024·包头)如图7-25-9,正方形ABCD的边长为2,以AB所在直线为轴,将正方形ABCD旋转一周,所得圆柱的主视图的面积为 ( )
A. 8
B. 4
C. 8π
D. 4π
图7-25-9
A
3. (2024·德阳,数学文化)走马灯,又称仙音烛,据史料记载,走马灯的历史起源于隋唐时期,盛行于宋代,是中国特色工艺品,常见于除夕、元宵、中秋等节日.在一次综合实践活动中,一同学用如图7-25-10所示的纸片,沿折痕折合成一个棱锥形的“走马灯”,正方形做底,侧面有一个三角形面上写了“祥”字,当灯旋转时,正好看到“吉祥如意”的字样.则在A,B,C处依次写上的字可以是 ( )
A. 吉、如、意 B. 意、吉、如
C. 吉、意、如 D. 意、如、吉
图7-25-10
A
温馨提示:此类考题常见于广东省中考数学试卷的选择或填空题,分值一般为3分.
【典型错例】画三视图时漏画了被遮挡部分的轮廓线
4. 如图7-25-11,画出下面几何体的三种视图.(注意符合三视图原则)
图7-25-11
解:如答图7-25-3.
答图7-25-3
错解分析
错解:如图7-25-12.
剖析:该解题过程的错误在于漏画了被遮挡部分的轮廓线.画几何体的三视图时要注意,几何体看得见部分的轮廓线画成实线,被其他部分遮挡而看不见的部分的轮廓线画成虚线.
图7-25-12
【生长式训练】知识生长→变式创新
5. (中考创新,原创题)如图7-25-13,AB,CD是直立在地面上的两根立柱,BE是立柱AB的影子.
知识种子:基本概念
(1)立柱在太阳光下的影子属于 ,立柱在路灯下的影子属于 ;(填“平行投影”或“中心投影”)
图7-25-13
平行投影
中心投影
种子生长:平行投影
(2)如图7-25-13,某一时刻在太阳光下,立柱AB在地面上的影子长BE=2 m.
①在图中画出此时立柱CD在太阳光下的影子DF;
图7-25-13
解:①如答图7-25-4,DF即为立柱CD在太阳光下的影子.
答图7-25-4
②若立柱AB=3 m,CD=2 m,求影子DF的长;
答图7-25-4
生长变式:投影变式
(3)如图7-25-14,在路灯下,立柱AB的影子为BE,立柱CD的影子为DF.
①请你确定灯泡所在的位置;
图7-25-14
解:①如答图7-25-5,点O即为灯泡所在的位置.
答图7-25-5
②若立柱AB=CD=2 m,影子BE=1 m,DF=3 m,立柱间的距离BD=16 m,求灯泡的高度;
答图7-25-5
种子成树:综合创新
(4)如图7-25-15,在路灯下,立柱AB的影子为BE,立柱CD的影子为DF.
①请你确定灯泡所在的位置;
图7-25-15
解:①如答图7-25-6,点P即为灯泡所在的位置.
答图7-25-6
②若立柱AB=4 m,CD=2 m,影子BE=3 m,DF=4 m,立柱间的距离BD=5 m,求灯泡的高度.
答图7-25-6
中考演练
(限时15分钟)
一、选择题
1. (2024·呼和浩特)如图7-25-16所示的几何体,其主视图是 ( )
A
图7-25-16
2. (2024·乐山,数学文化)下列文物中,俯视图是四边形的是( )
D
3. (2024·长春)南湖公园是长春市著名旅游景点之一.图7-25-17①是公园中“四角亭”景观的照片,图7-25-17②是其航拍照片,则图7-25-17③是“四角亭”景观的 ( )
A. 主视图
B. 俯视图
C. 左视图
D. 右视图
图7-25-17
B
4. (2024·凉山州)如图7-25-18,一块面积为60 cm2的三角形硬纸板(记为△ABC)平行于投影面时,在点光源O的照射下形成的投影是△A1B1C1.若OB∶BB1=2∶3,则△A1B1C1的面积是 ( )
A. 90 cm2
B. 135 cm2
C. 150 cm2
D. 375 cm2
图7-25-18
D
5. (2024·牡丹江)由5个形状、大小完全相同的小正方体组合而成的几何体,其主视图和左视图如图7-25-19所示,则搭建该几何体的方式有 ( )
A. 1种 B. 2种
C. 3种 D. 4种
图7-25-19
C
二、填空题
6. (2023·成都)一个几何体由几个大小相同的小立方块搭成,它的主视图和俯视图如图7-25-20所示,则搭成这个几何体的小立方块最多有
个.
图7-25-20
6
7. (2022·青海)由若干个相同的小正方体构成的几何体的三视图如图7-25-21所示,那么构成这个几何体的小正方体的个数是 .
图7-25-21
5
8. (2023·无锡)若直三棱柱的上下底面为正三角形,侧面展开图是边长为6的正方形,则该直三棱柱的表面积为 .
三、解答题
9. (教材改编)如图7-25-22是由同样大的小正方体拼成的图形.
(1)请你将该几何体的主视图和俯视图画在下面的方格图中;
(2)至少再添上 个这样的小正方体,就能将原图拼成一个较大的正方体.
图7-25-22
解:(1)如答图7-25-7.
答图7-25-7
19
10. (2023·南京节选)如图7-25-23,玻璃桌面与地面平行,桌面上有一盏台灯和一支铅笔,点光源O与铅笔AB所确定的平面垂直于桌面.在灯光照射下,AB在地面上形成的影子为CD(不计折射),AB∥CD.在桌面上沿着直线AB方向平移铅笔,试说明CD的长度不变.
图7-25-23
答图7-25-8
命题趋势
( 限时 5 分钟)
(创新题,数学文化)土圭之法是在平台中央竖立一根6尺长的杆子,观察杆子的日影长度. 古代的人们发现,夏至时日影最短,冬至日影最长,这样通过日影的长度得到夏至和冬至,确定了四季. 如图7-25-24是利用土圭之法记录了两个时刻杆的影长,发现第一时刻光线与杆的夹角∠BAC和第二时刻光线与地面的夹角∠ADB相等,测得第一时刻的影长为1.5尺,求第二时刻的影长为多少尺.
图7-25-24
命题解读:根据最新课程标准和近三年中考命题动向,预测2025年中考命题方向可能注重对三视图的考查,包括由几何体判断三视图以及由三视图还原几何体,可能会涉及较复杂的几何体;强调几何体展开与折叠,如考查正方体或其他常见几何体的展开图;还可能会考查投影的实际应用,如与生活中的光线照射、物体影子等结合,也可能与数学文化相结合.
第七章 尺规作图及图形变换
第25课时 投影与视图
课前循环练
(限时5分钟)
1. (广东真题)以下问题不适合全面调查的是 ( )
A. 调查某班学生每周课前预习的时间
B. 调查某中学在职教师的身体健康状况
C. 调查全国中小学生课外阅读情况
D. 调查某校篮球队员的身高
C
2. (广东真题)如图7-25-1是由几个大小相同的小正方体搭成的几何体的俯视图,小正方形中的数字表示该位置小正方体的个数,则该几何体的左视图是 ( )
A
3. (广东真题)将抛物线y=x2-4x-4向左平移3个单位长度,再向上平移5个单位长度,得到抛物线的函数表达式为 ( )
A. y=(x+1)2-13 B. y=(x-5)2-3
C. y=(x-5)2-13 D. y=(x+1)2-3
D
图7-25-2
70
5. (广东真题)某商店经销一种品牌的洗衣机,其中某一型号的洗衣机每台进价为a元,商店将进价提高20%后作为零售价进行销售,一段时间后,商店又以九折优惠价促销,这时该型号洗衣机的零售价为 元.
1.08a
①通过丰富的实例,了解中心投影和平行投影的概念.
②会画直棱柱、圆柱、圆锥、球的主视图、左视图、俯视图,能判断简单物体的视图,并会根据视图描述简单的几何体.
③了解直棱柱、圆锥的侧面展开图,能根据展开图想象和制作模型.
④通过实例,了解上述视图与展开图在现实生活中的应用.
课标要求
对接教材 人教:九下第二十九章 投影与视图
北师:七上第一章 丰富的图形世界;九上第五章 投影与视图
考点梳理
考点复习
1.投影
(1)中心投影:从 发出的光线所形成的投影称为中心投影.
(2)平行投影:由 光线所形成的投影称为平行投影.
(3)正投影:平行光线与投影面 时,这种投影称为正投影
一个点
平行
垂直
广东省对应考点例题
例1. 小龙同学拿一个矩形木框在阳光下摆弄,矩形木框在地面上形成的投影不可能是 ( )
D
2.三视图
视图:用 的方法绘制的物体在投影面上的图形,称为物体的视图.
(1)主视图:从 得到的视图叫做主视图;
(2)左视图:从 得到的视图叫做左视图;
(3)俯视图:从 得到的视图叫做俯视图
正投影
正面
左面
上面
例2. 若某几何体的三视图如图7-25-3所示,则该几何体是 ( )
A
3.三视图的画法
(1)画三视图要注意三个方面:主视图与俯视图 ;主视图与左视图 ;左视图与俯视图 .简记为“主俯长对正,主左高平齐,左俯宽相等”.
(2)注意实线与虚线的区别:能看到的线用实线,看不到的线用虚线
长度相等
高度相等
宽度相等
例3. 6个完全相同的正方体组成如图7-25-4所示的几何体,画出该几何体的主视图和左视图(画在所给的方格中).
图7-25-4
解:如答图7-25-1.
答图7-25-1
4.几何体的展开与折叠
(1)常见几何体的展开图
长方体 圆柱 圆锥 正三棱柱
(2)正方体的展开图
①“一四一”型
②“二三一”型
③“三三”型 ④“二二二”型
例4. (1)下列展开图中,是正方体展开图的是 ( )
(2)下列图形中,为圆柱的侧面展开图的是 ( )
C
D
(3)如图7-25-5是一个直三棱柱,试画出它的侧面展开图,并求侧面展开图的面积.
图7-25-5
解:(3)直三棱柱的侧面展开图如答图7-25-2.
S侧面=(1.5+2+2.5)×3=18.
答图7-25-2
广东中考
1. (2019·广东题3,3分,简单组合体的三视图)如图7-25-6,由4个相同正方体组合而成的几何体,它的左视图是 ( )
A
如图7-25-6
2. (2021·广东题6,3分,几何体的展开图)如图7-25-7所示的图形是正方体展开图的有 ( )
A. 1个 B. 2个 C. 3个 D. 4个
图7-25-7
C
高分击破
【典型考点】三视图;几何体的展开图
1. (2024·宁夏)用5个大小相同的小正方体搭一个几何体,其主视图、左视图如图7-25-8②,现将其中4个小正方体按图7-25-8①方式摆放,则最后一个小正方体应放在 ( )
A. ①号位置 B. ②号位置
C. ③号位置 D. ④号位置
B
图7-25-8
2. (2024·包头)如图7-25-9,正方形ABCD的边长为2,以AB所在直线为轴,将正方形ABCD旋转一周,所得圆柱的主视图的面积为 ( )
A. 8
B. 4
C. 8π
D. 4π
图7-25-9
A
3. (2024·德阳,数学文化)走马灯,又称仙音烛,据史料记载,走马灯的历史起源于隋唐时期,盛行于宋代,是中国特色工艺品,常见于除夕、元宵、中秋等节日.在一次综合实践活动中,一同学用如图7-25-10所示的纸片,沿折痕折合成一个棱锥形的“走马灯”,正方形做底,侧面有一个三角形面上写了“祥”字,当灯旋转时,正好看到“吉祥如意”的字样.则在A,B,C处依次写上的字可以是 ( )
A. 吉、如、意 B. 意、吉、如
C. 吉、意、如 D. 意、如、吉
图7-25-10
A
温馨提示:此类考题常见于广东省中考数学试卷的选择或填空题,分值一般为3分.
【典型错例】画三视图时漏画了被遮挡部分的轮廓线
4. 如图7-25-11,画出下面几何体的三种视图.(注意符合三视图原则)
图7-25-11
解:如答图7-25-3.
答图7-25-3
错解分析
错解:如图7-25-12.
剖析:该解题过程的错误在于漏画了被遮挡部分的轮廓线.画几何体的三视图时要注意,几何体看得见部分的轮廓线画成实线,被其他部分遮挡而看不见的部分的轮廓线画成虚线.
图7-25-12
【生长式训练】知识生长→变式创新
5. (中考创新,原创题)如图7-25-13,AB,CD是直立在地面上的两根立柱,BE是立柱AB的影子.
知识种子:基本概念
(1)立柱在太阳光下的影子属于 ,立柱在路灯下的影子属于 ;(填“平行投影”或“中心投影”)
图7-25-13
平行投影
中心投影
种子生长:平行投影
(2)如图7-25-13,某一时刻在太阳光下,立柱AB在地面上的影子长BE=2 m.
①在图中画出此时立柱CD在太阳光下的影子DF;
图7-25-13
解:①如答图7-25-4,DF即为立柱CD在太阳光下的影子.
答图7-25-4
②若立柱AB=3 m,CD=2 m,求影子DF的长;
答图7-25-4
生长变式:投影变式
(3)如图7-25-14,在路灯下,立柱AB的影子为BE,立柱CD的影子为DF.
①请你确定灯泡所在的位置;
图7-25-14
解:①如答图7-25-5,点O即为灯泡所在的位置.
答图7-25-5
②若立柱AB=CD=2 m,影子BE=1 m,DF=3 m,立柱间的距离BD=16 m,求灯泡的高度;
答图7-25-5
种子成树:综合创新
(4)如图7-25-15,在路灯下,立柱AB的影子为BE,立柱CD的影子为DF.
①请你确定灯泡所在的位置;
图7-25-15
解:①如答图7-25-6,点P即为灯泡所在的位置.
答图7-25-6
②若立柱AB=4 m,CD=2 m,影子BE=3 m,DF=4 m,立柱间的距离BD=5 m,求灯泡的高度.
答图7-25-6
中考演练
(限时15分钟)
一、选择题
1. (2024·呼和浩特)如图7-25-16所示的几何体,其主视图是 ( )
A
图7-25-16
2. (2024·乐山,数学文化)下列文物中,俯视图是四边形的是( )
D
3. (2024·长春)南湖公园是长春市著名旅游景点之一.图7-25-17①是公园中“四角亭”景观的照片,图7-25-17②是其航拍照片,则图7-25-17③是“四角亭”景观的 ( )
A. 主视图
B. 俯视图
C. 左视图
D. 右视图
图7-25-17
B
4. (2024·凉山州)如图7-25-18,一块面积为60 cm2的三角形硬纸板(记为△ABC)平行于投影面时,在点光源O的照射下形成的投影是△A1B1C1.若OB∶BB1=2∶3,则△A1B1C1的面积是 ( )
A. 90 cm2
B. 135 cm2
C. 150 cm2
D. 375 cm2
图7-25-18
D
5. (2024·牡丹江)由5个形状、大小完全相同的小正方体组合而成的几何体,其主视图和左视图如图7-25-19所示,则搭建该几何体的方式有 ( )
A. 1种 B. 2种
C. 3种 D. 4种
图7-25-19
C
二、填空题
6. (2023·成都)一个几何体由几个大小相同的小立方块搭成,它的主视图和俯视图如图7-25-20所示,则搭成这个几何体的小立方块最多有
个.
图7-25-20
6
7. (2022·青海)由若干个相同的小正方体构成的几何体的三视图如图7-25-21所示,那么构成这个几何体的小正方体的个数是 .
图7-25-21
5
8. (2023·无锡)若直三棱柱的上下底面为正三角形,侧面展开图是边长为6的正方形,则该直三棱柱的表面积为 .
三、解答题
9. (教材改编)如图7-25-22是由同样大的小正方体拼成的图形.
(1)请你将该几何体的主视图和俯视图画在下面的方格图中;
(2)至少再添上 个这样的小正方体,就能将原图拼成一个较大的正方体.
图7-25-22
解:(1)如答图7-25-7.
答图7-25-7
19
10. (2023·南京节选)如图7-25-23,玻璃桌面与地面平行,桌面上有一盏台灯和一支铅笔,点光源O与铅笔AB所确定的平面垂直于桌面.在灯光照射下,AB在地面上形成的影子为CD(不计折射),AB∥CD.在桌面上沿着直线AB方向平移铅笔,试说明CD的长度不变.
图7-25-23
答图7-25-8
命题趋势
( 限时 5 分钟)
(创新题,数学文化)土圭之法是在平台中央竖立一根6尺长的杆子,观察杆子的日影长度. 古代的人们发现,夏至时日影最短,冬至日影最长,这样通过日影的长度得到夏至和冬至,确定了四季. 如图7-25-24是利用土圭之法记录了两个时刻杆的影长,发现第一时刻光线与杆的夹角∠BAC和第二时刻光线与地面的夹角∠ADB相等,测得第一时刻的影长为1.5尺,求第二时刻的影长为多少尺.
图7-25-24
命题解读:根据最新课程标准和近三年中考命题动向,预测2025年中考命题方向可能注重对三视图的考查,包括由几何体判断三视图以及由三视图还原几何体,可能会涉及较复杂的几何体;强调几何体展开与折叠,如考查正方体或其他常见几何体的展开图;还可能会考查投影的实际应用,如与生活中的光线照射、物体影子等结合,也可能与数学文化相结合.
同课章节目录
